Dynamic Programming I HKOI 2005 Training Advanced Group

Dynamic Programming I HKOI 2005 Training (Advanced Group) Liu Chi Man, cx

Prerequisites • • Functions Recursion Divide-and-conquer Asymptotic notations – O, 2

Go, Go! • Recurrence relation • Dynamic programming 3

Recurrence Relation • A mathematical relationship expressing fn as some combination of fi with i < n • Eric W. Weisstein. "Recurrence Relation. " From Math. World--A Wolfram Web Resource. http: //mathworld. wolfram. com/Recurrence. Relation. html • An equation which defines a sequence recursively • “Recurrence relation. " Wikipedia: The Free Encyclopedia. 10 May 2005, 20: 00 UTC. 13 May 2005 . • Examples • The Fibonacci numbers • F 0 = 0; F 1 = 1; Fn = Fn-1 + Fn-2 (for n = 2, 3, 4, …) • The sequence is (0, 1, 1, 2, 3, 5, 8, 13, 21, …) Base conditions Recurrence 4

Recurrence Relation • Examples • The positive integers • K 1 = 1; Kn = min { Ki Kn-i } + 1 (for n = 2, 3, 4, …) 1≤ i < n • The sequence is (1, 2, 3, 4, 5, …) • The product of two factorials • • H 0, 0 = 1; H 0, i = H 0, i-1 i (for i = 1, 2, 3, …); Hi, 0 = Hi-1, 0 i (for i = 1, 2, 3, …); Hi, j = Hi-1, j-1 i j (for i = 1, 2, 3, …; j = 1, 2, 3, …) 5

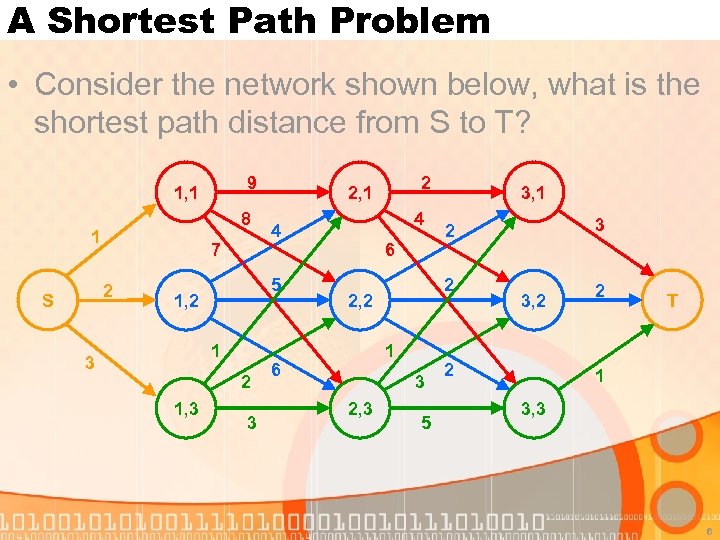A Shortest Path Problem • Consider the network shown below, what is the shortest path distance from S to T? 9 1, 1 8 1 7 2 S 1 3 2 1, 3 3 4 4 5 1, 2 2 2, 1 6 1 3 2, 3 5 3 2 2 2, 2 6 3, 1 3, 2 2 2 T 1 3, 3 6

A Shortest Path Problem • Solutions • Enumeration • • How many different paths are there? 3 3 3 = 27 Very small~ but what if we have (1, 1) up to (7, 7)? 7 7 = 823543 Still not too big~ How about (100, 100)? 100100 = (1 googol)2 [Note: 1 googol = 10100] Exponential growth! 7

A Shortest Path Problem • Solutions • Any shortest path algorithm on general graphs • Dijkstra • Bellman-Ford • Warshall-Floyd • Standard enough, but we can solve this problem more efficiently by exploiting some of its special properties • The graph shown is a so-called “layered network” • Each arrow goes from one layer to the next layer 8

A Shortest Path Problem • Notation (for convenience) • c(u, v) = the cost of the arrow from node u to node v • Definition • D(k) = the shortest path distance from S to node k • Base condition • D(S) = 0 • Recurrences • D(1, 1) = D(S) + c(S, (1, 1)); • D(1, 2) = D(S) + c(S, (1, 2)); • D(1, 3) = D(S) + c(S, (1, 3)); 9

A Shortest Path Problem • Recurrences • D(2, 1) = min { D(1, 1) + c((1, 1), (2, 1)), D(1, 2) + c((1, 2), (2, 1)), D(1, 3) + c((1, 3), (2, 1)) }; • D(2, 2) = min { D(1, 1) + c((1, 1), (2, 2)), D(1, 2) + c((1, 2), (2, 2)), D(1, 3) + c((1, 3), (2, 2)) }; • Similar for D(2, 3), D(3, 1), D(3, 2), D(3, 3) and D(T) • Final answer • D(T) 10

A Shortest Path Problem • Running time analysis • For each of the (roughly) 3 3 nodes, we perform • 3 additions • 1 “min” operation on 3 numbers • Let’s generalize to n n nodes • For each of the (roughly) n n nodes, we perform • n additions • 1 “min” operation on n numbers • Overall time complexity = (n 3), assuming that the D(. ) in min{…} can be retrieved in constant time 11

Dynamic Programming • A method for reducing the runtime of algorithms exhibiting the properties of overlapping subproblems and optimal substructure • “Dynamic programming. " Wikipedia: The Free Encyclopedia. 7 May 2005, 20: 01 UTC. 13 May 2005 . • In the previous example, why doesn’t our algorithm need to enumerate all possible paths from S to T? • Why we can compute D(2, 1) from D(1, 1), D(1, 2) and D(1, 3) so easily? 12

Optimal Substructure • A problem is said to have optimal substructure if its optimal solution can be constructed efficiently from optimal solutions to its subproblems • Optimal substructure. " Wikipedia: The Free Encyclopedia. 25 Mar 2005, 00: 48 UTC. 13 May 2005 . • In other words, the subsolution of an optimal solution is an optimal solution of the corresponding subproblem optimal Problem Subproblem optimal Solution optimal Subsolution 13

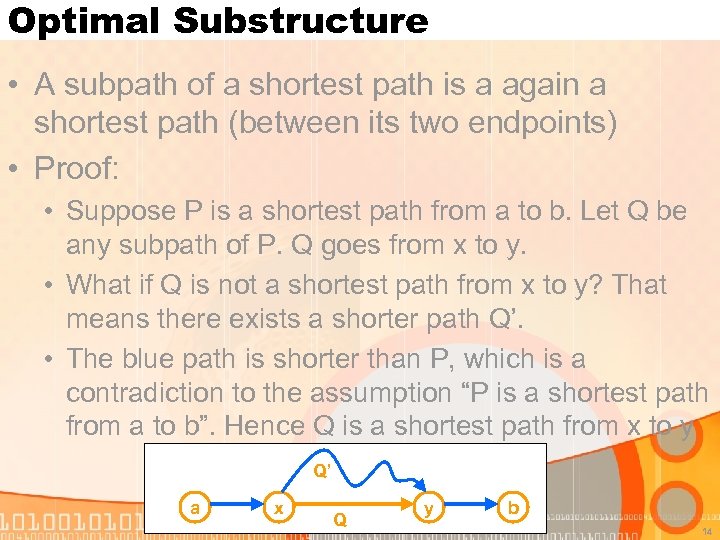Optimal Substructure • A subpath of a shortest path is a again a shortest path (between its two endpoints) • Proof: • Suppose P is a shortest path from a to b. Let Q be any subpath of P. Q goes from x to y. • What if Q is not a shortest path from x to y? That means there exists a shorter path Q’. • The blue path is shorter than P, which is a contradiction to the assumption “P is a shortest path from a to b”. Hence Q is a shortest path from x to y Q’ a x Q y b 14

Optimal Substructure • Thus the shortest path problem exhibits an optimal substructure • That’s why we can compute D(2, 1) from D(1, 1), D(1, 2) and D(1, 3) • Suppose we now want to compute D(m, k) • A path from S to (m, k) must path through either one of (m-1, 1), (m-1, 2), … , (m-1, n) • This implies that in particular, a SHORTEST path from S to (m, k) must path through one of those n nodes • But which one? ? 15

Optimal Substructure • How long is the shortest path from S to (m, k) passing through (m-1, i)? • From the optimal substructure, we know that the distance is D(m-1, i) + c((m-1, i), (m, k)) • D(m, k) is the minimum of these n distances, and we have obtained our recurrence 16

Optimal Substructure • Some problems do not exhibit optimal substructures • For example, finding a longest simple path in a graph between two nodes • A longest simple path from s to e is s b c d e • Is it true that b c is a longest simple path from d e b to c? c s b 17

Optimal Substructure • Let’s try (and fail) to set up a recurrence relation for the longest simple path problem • Definition • L(v) = the longest simple path distance from node s to node v • Base condition • L(s) = 0 • For the recurrence part, we use our previous reasoning… 18

Optimal Substructure • Let u 1, u 2, …, uk be the nodes preceding v • Then a longest simple path from s to v must pass through one of u 1, u 2, …, uk • How long is the longest simple path from s to v passing through u 1? • L(u 1) + 1 … Wait! What’s wrong? • v may lie on the longest simple path from s to u 1 • We cannot set up a recurrence easily • This is because of the absence of an optimal substructure 19

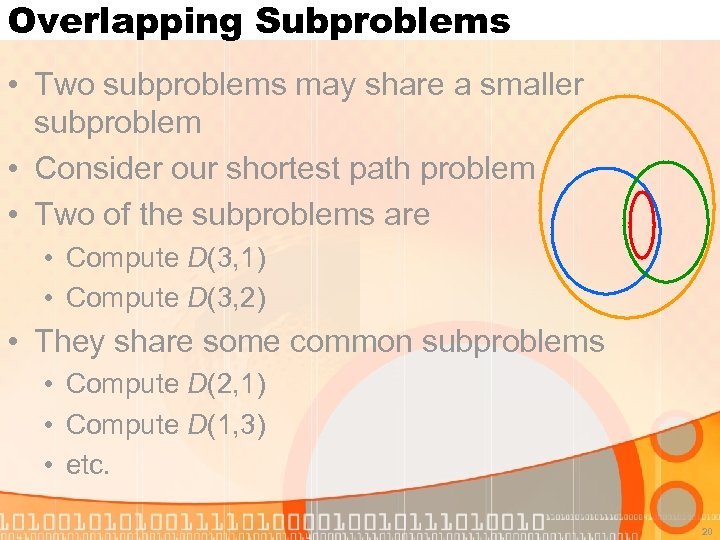Overlapping Subproblems • Two subproblems may share a smaller subproblem • Consider our shortest path problem • Two of the subproblems are • Compute D(3, 1) • Compute D(3, 2) • They share some common subproblems • Compute D(2, 1) • Compute D(1, 3) • etc. 20

Overlapping Subproblems • Suppose we want to compute D(2, 1) and D(2, 2) • Computing D(2, 1) requires computing D(1, 1), D(1, 2) and D(1, 3), and each of them requires computing D(S) • Then we compute D(2, 2) • Computing D(2, 2) requires computing D(1, 1), D(1, 2) and D(1, 3), and each of them requires computing D(S) • Note the repetitions of computations! • Try to compute D(3, 1) and D(3, 2) 21

Overlapping Subproblems • We store every D(. ) in memory after computing its value • When computing a D(. ), we can simply retrieve previously computed D(. )s from memory, avoiding repeated computations of those D(. )s • So, for our shortest path problem, the D(. )s in min{…} can be “computed” in constant time • Our algorithm runs in (n 3) time! 22

How to Solve a Problem by DP? • Determine whether the problem exhibits an optimal substructure and has overlapping subproblems • If so, then it MAY be solvable by DP • Try to formulate a recurrence relation for the optimal solution (this is the most difficult step) • Based on the recurrence relation, design an algorithm that compute the function values in correct order • You are done 23

How to Solve a Problem by DP? • If you are experienced enough, you may write up the recurrence before you identify any optimal structure or overlapping subproblems • A problem may have many different formulations; some are easier to reach, while the others are easier to implement • Sometimes when you identify a problem as a DP-able problem, you are 90% done • We are going to see a few classical DP examples 24

Longest Common Subsequence • Given two strings A and B of length n and m respectively, find their longest common subsequence (NOT substring) • Example • • A: aabcaadyyyefg B: cdfehgjaefazadxex LCS: caaade Explanation • A: a a b c a a d y y y e f g • B: c d f e h g j a e f a z a d x e x 25

Longest Common Subsequence • Solution • Exhaustion • Number of subsequences of A = 2 n • Exponential time! • Optimal substructure • A: a a b c a a d y y y e f g • B: c d f e h g j a e f a z a d x e x • caa is the LCS of caabca and cdfehgjaefa • Proof: similar to the “shortest path” proof • Overlapping subproblems • Obvious 26

Longest Common Subsequence • Definition • Fi, j = length of LCS of A[1. . i] and B[1. . j] • Base conditions • Fi, 0 = 0 for all i • F 0, j = 0 for all j • Recurrence • Fi, j = Fi-1, j-1 + 1 (if A[i] = B[j]) max{ Fi-1, j , Fi, j-1 } (otherwise) • Answer • Fn, m 27

Longest Common Subsequence • Explanation of the recurrence • If A[i] = B[j], then matching A[i] and B[j] as a pair has no bad effect • A: ? ? ? ? x? ? ? ? • B: ? ? ? ? ? x? ? ? • How about the blue portion? • I don’t care, but according to the optimal structure, we should use the LCS of the two blue strings • Therefore we have Fi, j = Fi-1, j-1 + 1 28

Longest Common Subsequence • Explanation of the recurrence • If A[i] B[j], then either A[i] or B[j] (or both) must not appear in a LCS of A[1. . i] and B[1. . j] • If A[i] does not appear (B[j] MAY appear) • • A: ? ? ? ? x? ? ? ? B: ? ? ? ? ? y? ? ? LCS of A[1. . i] and B[1. . j] = LCS of blue strings Fi, j = Fi-1, j • If B[j] does not appear (A[i] MAY appear) • • A: ? ? ? ? x? ? ? ? B: ? ? ? ? ? y? ? ? LCS of A[1. . i] and B[1. . j] = LCS of blue strings Fi, j = Fi, j-1 29

Longest Common Sequence • Can we compute Fn, m directly? • No, we need to compute Fn-1, m, Fn, m-1, Fn-1, m-1 first • Therefore we must compute the Fs in the “safe” order • For example, we can compute the Fi, js in increasing order of i and j • Now I know the length of the LCS, but how to obtain the LCS? • Exercise 30

Longest Common Subsequence • Store base conditions in memory for i = 1 to n do for j = 1 to m do Compute Fi, j Store Fi, j in memory The answer is Fn, m • Time complexity = (nm) • Space complexity = (nm) • Can be reduced to (min{n, m}) • Wait for DP 2 31

Stones • There are n piles of stones in a row • The piles have, in order, a 1, a 2, …, an stones respectively • You can merge two adjacent piles of stones, paying a cost which is equal to the number of stones in the resulting pile • Find the minimum cost to merge all stones into one single pile 32

Stones • Sample play • • • 41275 4375 7 12 19 Total cost = 3 + 7 + 12 + 19 = 41 • Does a greedy strategy always work? 33

Stones • Suppose after some moves, there are m piles left and the numbers of stones in the piles are b 1, b 2, …, bm • Each bi corresponds to a contiguous sequence of original (unmerged) piles • Example: • 876123123435 • 15 12 1 2 7 8 34

Stones • Optimal substructure • Suppose in an optimal (minimum cost) solution, after some steps, there are m piles left • Choose one of these piles, say p • Suppose p corresponds to original piles s, s+1, …, t • We claim that in the optimal solution, the sequence of moves that transform original piles s, s+1, …, t into p is an optimal solution to the subproblem [as, as+1, …, at] • The proof is trivial 35

Stones • Overlapping subproblems • Obvious • Definition • Ci, j = minimum cost to merge original piles i, i+1, …, j-1, j into a single pile • Base conditions • Ci, i = 0 for all i • Recurrence (for i < j) j • Ci, j = min { Ci, k + Ck+1, j + ax } i≤k

Stones • Explanation of the recurrence • To merge original piles i, i+1, …, j, there must be a (final) step in which we merge two piles into one • Let the two piles be p and q, where p corresponds to original piles i, i+1, …, k and q corresponds to original piles k+1, k+2, …, j j • The cost to merge p and q = ax x=i • The minimum cost to construct p = Ci, k • The minimum cost to construct q = Ck+1, j • By the optimal substructure, the total cost is j Ci, k + Ck+1, j + ax x=i 37

Stones • In what order we should compute Ci, j? • Increasing i and j? No! • Recall: what does Ci, j depend on? • We can compute Ci, j in increasing (j-i) order We are computing this . . . and we need these . . . i i+1 i+2 i+3 i+4 j-2 j-1 j 38

Stones • To avoid all the fuss in the previous slide, we may use a top-down implementation • function get. C(i, j) { if Ci, j is already computed, Return Ci, j otherwise Compute Ci, j using get. C() calls Store Ci, j in memory Return Ci, j } • No need to care about the order of computations! 39

Stones • Time complexity = (n 3) • By using a really clever trick (quadrangle inequality) we can modify the algorithm to run in (n 2), but that’s too far from our discussion • Space complexity = (n 2) • You may try another formulation • Define C’i, h = minimum cost to merge original piles i, i+1, i+2, …, i+h-1 into a single pile • What are the advantages and disadvantages of this formulation? 40

Speeding Up Computation of R. F. • The computation of some recursive (mathematical) functions (e. g. the Fibonacci numbers) can be sped up by “dynamic programming” • However, this computation does not exhibit an optimal substructure • In fact, optimality doesn’t mean anything here • We make use of memo(r)ization (storing computed values in memory) to deal with overlapping subproblems 41

Memo(r)ization • To be precise, we use the term memoization or memorization to refer to the method for speeding up computations by storing previously computed results in memory • The term memoization comes from the noun memo • The term dynamic programming refers to the process of setting up and evaluating a recurrence relation efficiently by employing memo(r)ization 42

Memo(r)ization • However, in reality, memo(r)ization is often replaced by dynamic programming • Let’s start the good(? ) practice in HKOI • HKOI DP Revolution of 2005 • We: Orz 43

0 -1 Knapsack • The notion of subproblems is not very obvious in some problems • There are n items in a shop. The i-th item has weight wi and value vi. A thief has a knapsack which can carry at most a weight of W. What should she steal to maximize the total value of the stolen items? • Assumption: all numbers in this problem are positive integers • Bonus exercise: what does 0 -1 mean? 44

0 -1 Knapsack • What is a subproblem? • Less weight, fewer items • Identify the optimal substructure • Exercise • Definition • Ti, j = maximum value she gains if she is allowed to choose from items 1, 2, …, i and the weight limit is j • T’i, j = maximum value she gains if item i is the largest indexed item chosen and the weight limit is j • Which one is better? 45

0 -1 Knapsack • Base conditions • Ti, 0 = 0 for all i • T’i, 0 = 0 for all i • Recurrence (for i, j > 0) • Ti, j = max { Ti-1, j, Ti-1, j-wi + vi } Ti-1, j • T’i, j = max { Tk, j-wi + vi } 1 ≤ k < i, T >0 vi 0 k, j-wi (if wi ≤ j) (otherwise) (if wi < j) (if wi = j) (otherwise) 46

0 -1 Knapsack • Time complexity • T version – O(n. W) • T’ version – O(n 2 W) • T’ is much more difficult to formulate and results in a higher time complexity • This shows that the definition of the optimal function should be chosen carefully • Again, it is your exercise to give an algorithm to construct the optimal set of chosen items 47

0 -1 Knapsack • In the Branch-and-Bound lecture I was told that the 0 -1 Knapsack problem is NP-complete, but why there exists a polynomial-time DP solution? • Polynomial in which variables? • What assumptions have we made in the problem statement? 48

Phidias • An easy problem at IOI 2004 • Phidias (an ancient Greek sculptor) has a big rectangle of size W H. He wants to cut the rectangle into small rectangles. Each small rectangle should have size W 1 H 1, or W 2 H 2, …, or Wn Hn. If any piece left is not of any of those sizes, then it is wasted. Phidias can only cut straight through a rectangle (parallel to a side of the rectangle), leaving two smaller rectangles. What is the minimum possible wasted area? 49

Phidias • Subproblem: cutting a smaller rectangle • Optimal substructure: Phidias cut according to an optimal solution. After some cuts, choose any one rectangle. In the optimal solution, this rectangle is going to be cut in a way that the wasted area is at minimum (concerning only this rectangle). • Proof: trivial, because how this rectangle is cut should be independent of other rectangles left 50

Phidias • Definition • Ph, w = min. wasted area if a h w rectangle is cut • Base conditions • P 1, 1 = 0 1 • PHi, Wi = 0 (if 1 1 is one of the n desired sizes) (otherwise) (for 1 ≤ i ≤ n) • Recurrence • Ph, w = min { 1 minh { Pk, w + Ph-k, w }, 1 ≤ k < w{ Ph, k + Ph, w-k } } min ≤k< • Answer • PH, W 51

Looking forward… • Topics going to be covered in Dynamic Programming II • • Fantastic DP formulations Dimension reduction in space DP on trees and graphs and hopefully, minimax for two-person games 52