9091df35579f153b2babdf88152749fe.ppt
- Количество слайдов: 27

Dynamic Programming Examples Based on: 1. Michael A. Trick: A Tutorial on Dynamic Programming http: //mat. gsia. cmu. edu/classes/dynamic. html 2. M. A. Rosenman: Tutorial - Dynamic Programming Formulation 1. http: //people. arch. usyd. edu. au/~mike/Dynamic. Prog/DPTutorial. 95. ht ml

Motivation Problems • • Capital Budgeting Problem Minimum cost from Sydney to Perth Economic Feasibility Study Travelling Salesman Problem

Capital Budgeting Problem • • A corporation has $5 million to allocate to its three plants for possible expansion. Each plant has submitted a number of proposals specifying (i) the cost of the expansion c and (ii) the total revenue expected r. Each plant is only permitted to realize one of its proposals. The goal is to maximize the firm’s revenues resulting from the allocation of the $5 million. Investment proposals Plant 1 Proposal Plant 2 Plant 3 c 1 r 1 1 0 0 0 2 1 5 2 8 1 4 3 2 6 3 9 - - 4 12 - -

Minimum cost from Sydney to Perth • • • Travelling from home in Sydney to a hotel in Perth – choose from 3 hotels. Three stopovers on the way – a number of choices of towns for each stop. Each trip has a different distance resulting in a different cost (petrol). Hotels have different costs. The goal is to select a route to and a hotel in Perth so that the overall cost of the trip is minimized.

Economic Feasibility Study • We are asked for an advice how to best utilize a large urban area in an expanding town. • Envisaged is a mixed project of housing, retil, office and hotel areas. • Rental income is a function of the floor areas allocated to each activity. • The total floor area is limited to 7 units. • The goal is to find the mix of development which will maximize the return. • Additional constraint determines that the project must include at least 1 unit of offices.

Traveling Salesman Problem • Given a number of cities and the costs of travelling from any city to any other city, what is the cheapest round-trip route that visits each city exactly once and then returns to the starting city? • Example Optimized tour Random tour New York 1. New York 2. Miami 1334 3. Dallas 1559 4. Chicago 809 Miami 1334 1343 1397 Dallas 1559 1343 921 Chicago 809 1397 921 -

How to Solve it? No problem, just try all possibilities and choose the best. It is not that easy for problem instances of a realistic size. Try it out!

DP: Common characteristics • • The problem can be divided into stages with a decision required at each stage. Each stage has a number of states associated with it. The decision at one stage transforms one state into a state in the next stage. Principal of optimality: Given the current state, the optimal decision for each of the remaining states does not depend on the previous states or decisions. • There exists a recursive relationship that identifies the optimal decision for stage j, given that stage j+1 has already been solved. • The final stage must be solvable by itself. • It is an art to determine stages and states.

DP: Capital Budgeting Problem • Stages – money allocated to a single plant • States variables x 1 = {0, 1, 2, 3, 4, 5} … amount of money spent on plant 1 x 2 = {0, 1, 2, 3, 4, 5} … amount of money spent on plant 1 and 2 x 3 = {5} … amount of money spent on palnts 1, 2 and 3 We want x 3 to be 5. • Ordering on the stages – first allocate to plant 1, then plant 2, then plant 3.
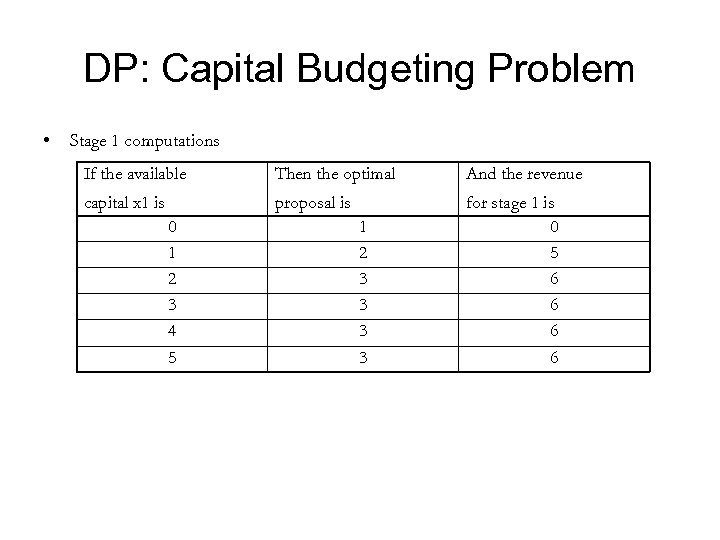
DP: Capital Budgeting Problem • Stage 1 computations If the available Then the optimal And the revenue capital x 1 is proposal is for stage 1 is 0 5 6 6 0 1 2 3 4 5 1 2 3 3
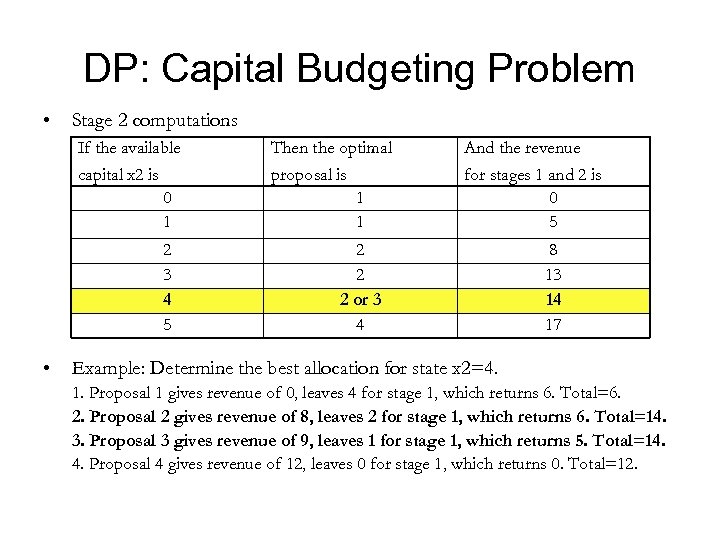
DP: Capital Budgeting Problem • Stage 2 computations If the available capital x 2 is 0 1 2 3 4 5 • Then the optimal proposal is 1 1 And the revenue for stages 1 and 2 is 0 5 2 2 2 or 3 4 8 13 14 17 Example: Determine the best allocation for state x 2=4. 1. Proposal 1 gives revenue of 0, leaves 4 for stage 1, which returns 6. Total=6. 2. Proposal 2 gives revenue of 8, leaves 2 for stage 1, which returns 6. Total=14. 3. Proposal 3 gives revenue of 9, leaves 1 for stage 1, which returns 5. Total=14. 4. Proposal 4 gives revenue of 12, leaves 0 for stage 1, which returns 0. Total=12.

DP: Capital Budgeting Problem • Stage 3 computations, we are interested in x 3=5 1. Proposal 1 gives revenue 0, leaves 5. Previous stages give 17. Total=17. 2. Proposal 2 gives revenue 4, leaves 4. Previous stages give 14. Total=18. • The optimal solution, that gives a revenue 18, is to implement - proposal 2 at plant 3, - proposal 2 or 3 at plant 2, and - proposal 3 or 2 at plant 1.
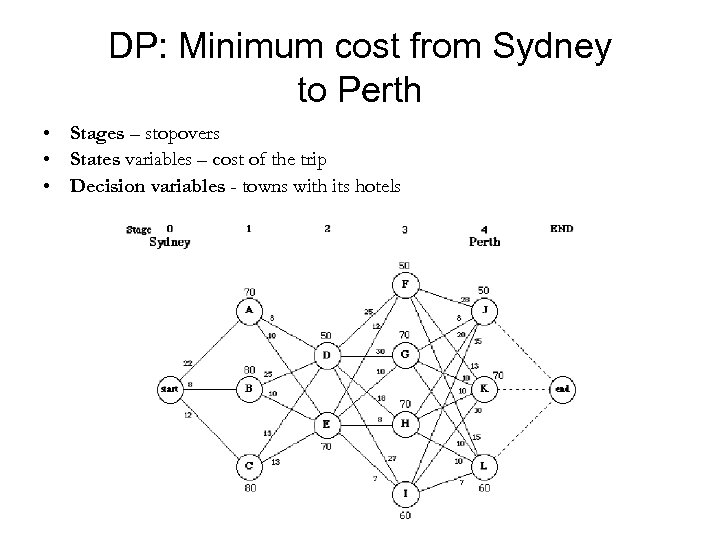
DP: Minimum cost from Sydney to Perth • Stages – stopovers • States variables – cost of the trip • Decision variables - towns with its hotels

DP: Minimum cost from Sydney to Perth
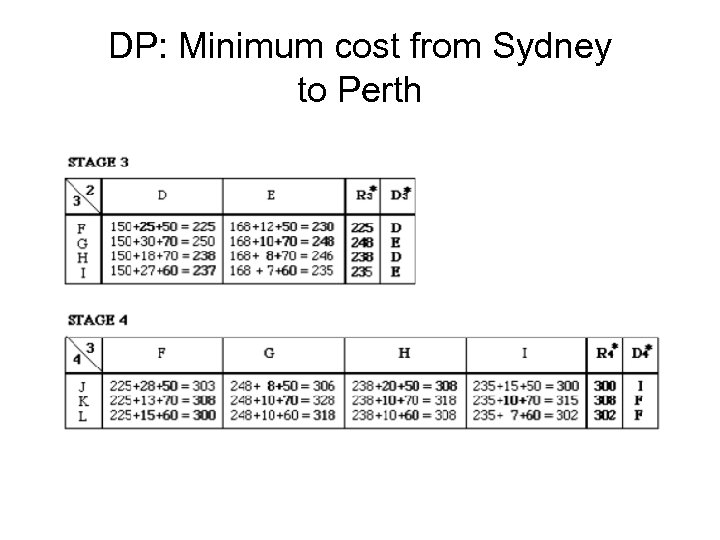
DP: Minimum cost from Sydney to Perth
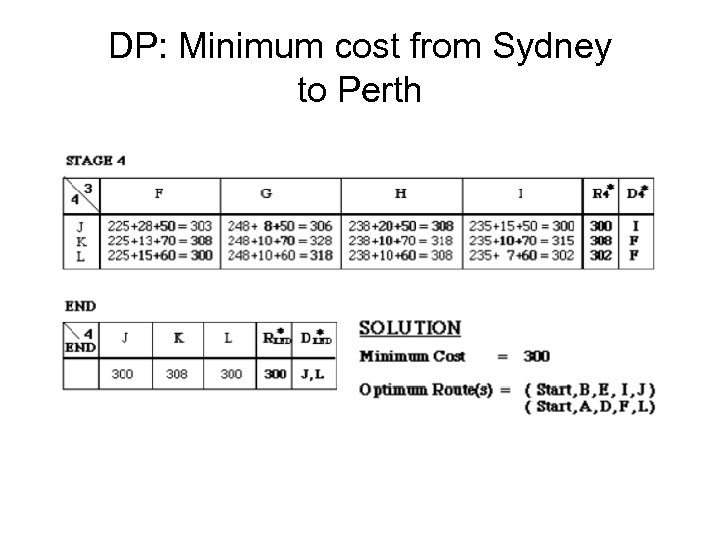
DP: Minimum cost from Sydney to Perth

DP: Economic Feasibility Study • Stage variable – the development type (1, 2, 3, 4) • State variable – the amount of floor area allocated to all dev. types • Decision variables – the amount of floor area allocated to the nth dev. type
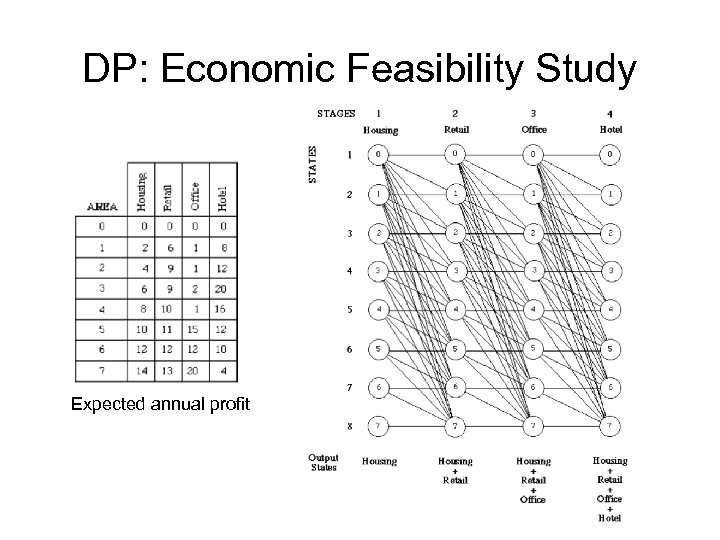
DP: Economic Feasibility Study Expected annual profit
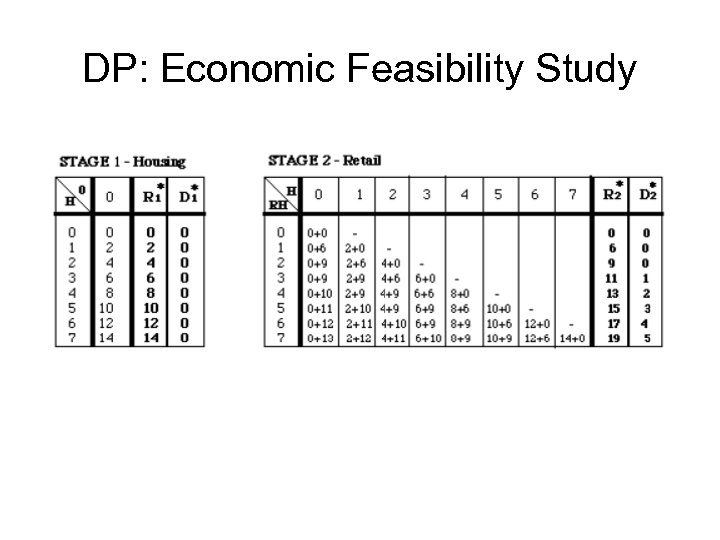
DP: Economic Feasibility Study

DP: Economic Feasibility Study

DP: Economic Feasibility Study How we get it?
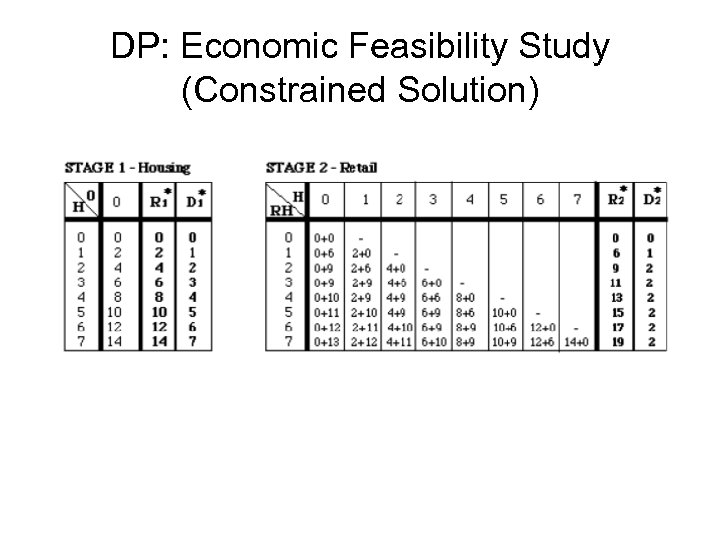
DP: Economic Feasibility Study (Constrained Solution)
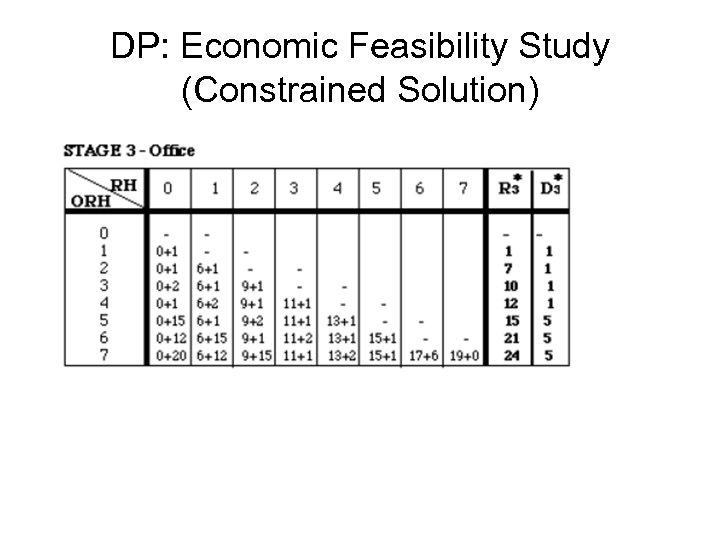
DP: Economic Feasibility Study (Constrained Solution)

DP: Economic Feasibility Study (Constrained Solution) Solution?

DP: Economic Feasibility Study (Constrained Solution)
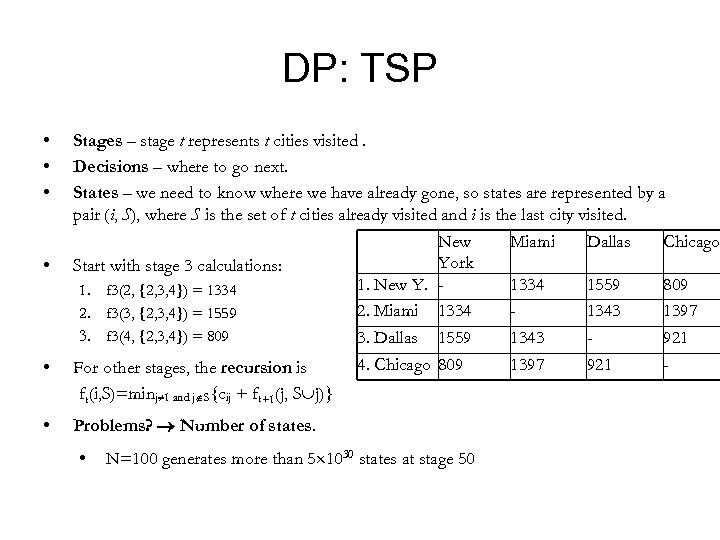
DP: TSP • • Stages – stage t represents t cities visited. Decisions – where to go next. States – we need to know where we have already gone, so states are represented by a pair (i, S), where S is the set of t cities already visited and i is the last city visited. Start with stage 3 calculations: 1. f 3(2, {2, 3, 4}) = 1334 2. f 3(3, {2, 3, 4}) = 1559 3. f 3(4, {2, 3, 4}) = 809 • For other stages, the recursion is ft(i, S)=minj 1 and j S{cij + ft+1(j, S j)} • New York 1. New Y. 2. Miami 1334 3. Dallas 1559 4. Chicago 809 Problems? Number of states. • N=100 generates more than 5 1030 states at stage 50 Miami Dallas Chicago 1334 1343 1397 1559 1343 921 809 1397 921 -

Need for Something Better! • Curse of dimmensionality – Not enough memory, not enough computational power to solve hard problems. • Softcomputing techniques - Evolutionary algortihms, Artificial neural networks, Fuzzy. – The guiding principle of soft computing is: Exploit the tolerance for imprecision, uncertainty, partial truth, and approximation to achieve tractability, robustness and low solution cost.
9091df35579f153b2babdf88152749fe.ppt