DYNAMIC CONDITIONAL CORRELATION ECONOMETRIC RESULTS AND FINANCIAL

DYNAMIC CONDITIONAL CORRELATION : ECONOMETRIC RESULTS AND FINANCIAL APPLICATIONS Robert Engle New York University Prepared for CARLOS III, MAY 24, 2004

ABSTRACT A new model for measuring and predicting correlations as well as volatilities is examined. This Dynamic Conditional Correlation model or DCC, models the volatilities and correlations in two steps. The specification of the correlation dynamics is extended to allow asymmetries important for financial practice. The presentation develops the econometric methods for estimating the DCC model. The DCC provides a joint density function with tail dependence greater than the normal. This is explored both by simulation and empirically. The time aggregated DCC is presented as a useful copula for financial decision making. As an example, a covariance matrix is estimated between 34 country equity and bond returns. The role of asymmetry is examined in both volatilities and correlations. The dispersion of equity and bond volatilities and their pairwise correlations are examined over time and after the formation of the EURO.

OUTLINE n n WHAT IS DCC? ESTIMATION THEORY n n BEYOND LINEAR DEPENDENCE n n n TWO STEP QMLE STANDARD ERRORS DEPENDENCE MEASURES MULTI-STEP DISTRIBUTION ASYMMETRIC GLOBAL CORRELATIONS

Conditional Correlations n Definition of conditional correlation n And letting

Multivariate Definitions n n Let r be a vector of returns and D a diagonal matrix with standard deviations on the diagonal R is a time varying correlation matrix

DYNAMIC CONDITIONAL CORRELATION A NEW SOLUTION in Engle(2002) n THE STRATEGY: n n n ESTIMATE UNIVARIATE VOLATILITY MODELS FOR ALL ASSETS CONSTRUCT STANDARDIZED RESIDUALS (returns divided by conditional standard deviations) ESTIMATE CORRELATIONS BETWEEN STANDARDIZED RESIDUALS WITH A SMALL NUMBER OF PARAMETERS

MODELS FOR CONDITIONAL CORRELATIONS n Constant n Integrated Processes n Mean Reverting Processes n More complex multivariate processes

The Constant Correlation Estimator: Bollerslev(1990) n Let Be the standardized residuals n Then

Specifications for Rho n Exponential Smoother n i. e.

Mean Reverting Rho n Just as in GARCH

Simple Correlation Models and

Tse and Tsui(2002) n A closely related model for modeling correlations directly as a weighted average of three correlation matrices.

Higher Order Models Engle and Sheppard(2002), Theoretical and Empirical Properties of Dynamic Conditional Correlation Multivariate GARCH n Higher order DCC are estimated n Applied to 100 S&P industry sectors n Applied to 30 Dow Stocks

Higher Order DCC n Define DCC(p, q) as n For most of the data sets, DCC(1, 1) was adequate.

Generalized DCC n n n Add parameters for each asset Where A and B are square, symmetric, and is Hadamard product If A, B and (ii’-A-B) are p. s. d and R is p. d. , then Q is p. d. See Ding and Engle(2001)

Diagonal Generalized DCC n Choose a parameterization for A, B. n So that for any W n Hence for any i and j

Asymmetric DCC n n Response to two negative returns is different from overall response. Define Asymmetry can be introduced with terms that are zero except when both returns are negative such as: Or more generally (and averaging to zero):

Asymmetric Generalized DCC n n The Asymmetric Generalized DCC can be expressed And assuming a diagonal structure for A, B and G, the typical equation becomes

Log Likelihood

Two Step Maximum Likelihood n n First, estimate each return as GARCH possibly with other variables or returns as inputs, and construct the standardized residuals Second, maximize the conditional likelihood with respect to any unknown parameters in rho

ECONOMETRIC QUESTIONS n n With non-normal data, are these QMLE estimators? How can we construct asymptotically consistent standard errors? n n Let parameters in GARCH be and call the likelihood function QL 1 Let parameters in DCC be and call the second part of the likelihood function QL 2

Quasi Likelihood

GENERAL RESULT n n Bollerslev and Wooldridge(1992) show that any multivariate GARCH model that is correctly specified in the first two moments, and satisfies a bunch of regularity conditions, will be a QMLE estimator. However this does not imply that two step estimation is consistent.

Two Step Estimators See Newey and Mc. Fadden(1994) pp. 2176 -2184 n n n Suppose there are two sets of parameters ( , ) that are have no relation, i. e. are “variation free”. Let there be k 1 moment conditions g 1( ) and k 2 moment conditions g 2( , ), where these conform with the number of parameters in ( , ). Consider the GMM estimation min g’Wg with g=(g 1, g 2)’. n n It is just identified so W=I is no restriction. It will be a two step estimator since will solve only the first set of moments and will solve the second using the first estimate of .

GENERAL GMM RESULTS

KEY ASSUMPTION n n The first stage is consistent even if not MLE! That is GARCH models estimated individually are consistent but inefficient when all parameters are variation free.

For Two Step n Given consistency for all parameters

APPLICATION TO VARIANCE TARGETING n n n Variance Targeting was proposed by Engle and Mezrich(1995) to constrain an ARCH model to have a prespecified long run variance. Typically this was the sample variance. It is easily seen that the long run variance forecast from this model is 2 There are only two parameters to estimate rather than three.

ECONOMETRIC ISSUES n n Using the sample variance in this model gives This is not a Maximum Likelihood estimator of GARCH(1, 1) and therefore is asymptotically inefficient It will be consistent because the sample variance is consistent in a wide range of models. If GARCH is misspecified, the long run variance will still be consistent.

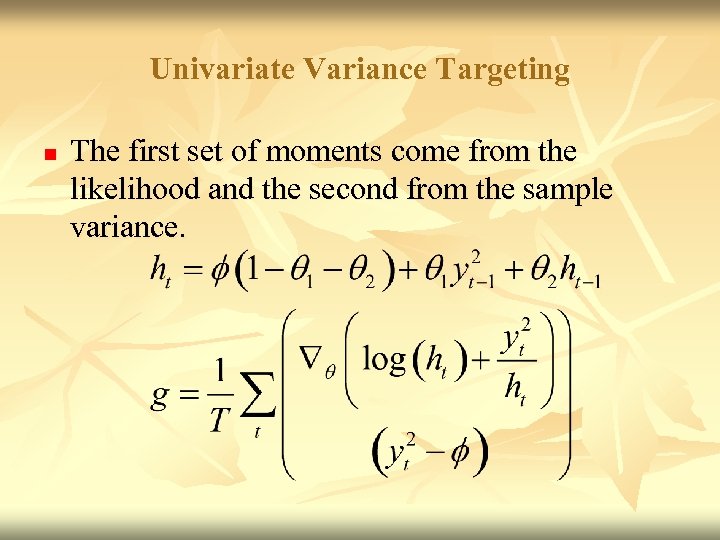Univariate Variance Targeting n The first set of moments come from the likelihood and the second from the sample variance.

Two Step DCC n One set of 3 n moments for the variance models, , and one set for the correlations, .

Three Step DCC or DCC with Correlation Targeting n One set of 3 n moments for variances, n(n -1)/2 for unconditional correlations, and two for the correlation process.

BEYOND LINEAR DEPENDENCE

JOINT DISTRIBUTIONS n n n Dependence properties are all summarized by a joint distribution For a vector of kx 1 random variables Y with cumulative distribution function F Assuming for simplicity that it is continuously differentiable, then the density function is:

UNIVARIATE PROPERTIES n n n For any joint distribution function F, there are univariate distributions Fi and densities fi defined by: is a uniform random variable on the interval (0, 1) What is the joint distribution of

COPULA n The joint distribution of these uniform random variables is called a copula; n n n it only depends on ranks and is invariant to monotonic transformations. Equivalently

COPULA DENSITY n n Again assuming continuous differentiability, the copula density is From the chain rule or change of variable rule, the joint density is the product of the copula density and the marginal densities

BIVARIATE DEPENDENCE MEASURES n n Pearson or simple correlation Will be sensitive to monotonic transformations of the data, I. e. to the marginal densities as well as the copula

Invariant Measures n Kendall’s Tau: For a bivariate vector Y, n n τ depends only on the ranks, ie on the copula Spearman or rank correlation

A NEW ESTIMATOR RANK-DCC n n A dynamic correlation estimator can be constructed based only on the order statistics of the data First create standardized residuals (? ) then rank them Build a DCC model based on rank data Estimator is less sensitive to outliers but pretty similar to cardinal DCC.

TAIL DEPENDENCE n When one variable is extreme, will another be also extreme? Upper tail dependence is n Lower tail dependence is n

Values of Tail Dependence n n Tail dependence is a probability and must be between zero and one For joint normal distributions: For other copulas one or both may be non-zero. It is interesting if lower tail is more dependent than upper

What is the Distribution of DCC? n n To focus on the comovements, let volatilities be constant and normalized to 1. Consider bivariate distribution of (y, x) n n n Conditional correlations are changing but there is only one unconditional correlation. This is therefore not a multivariate normal This is a mixture of normals n n with standard normal marginals With same covariance, on average.

Simulation n 100, 000 observations N n DCC n ADCC n

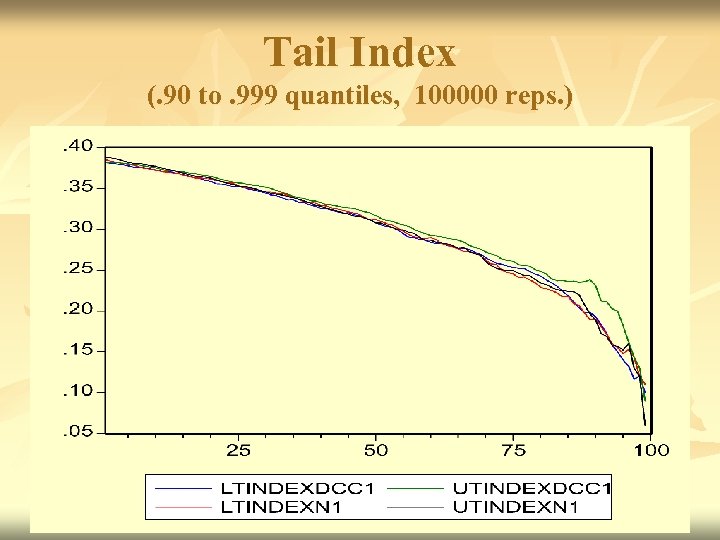Tail Index (. 90 to. 999 quantiles, 100000 reps. )

Discussion n n Small increase in tail correlations Very little evidence of non-zero tail index Still need to develop standard errors. Similar results for ADCC

Time Aggregation n Multiperiod correlations include new interesting effects n n n They are not individually normal A large comovement leads to large correlations and a subsequently large comovement. Expect two period aggregates to show this ADCC should show this especially in lower tail Average upper and lower tail for DCC as it is symmetric

Symmetric Tail Dependence P 2, T P 1, T

Lower Tail Dependence P 2, T P 1, T

P 2, T K 1 Put Option on asset 1 Pays P 1, T Both options Payoff Option on asset 2 Pays K 2

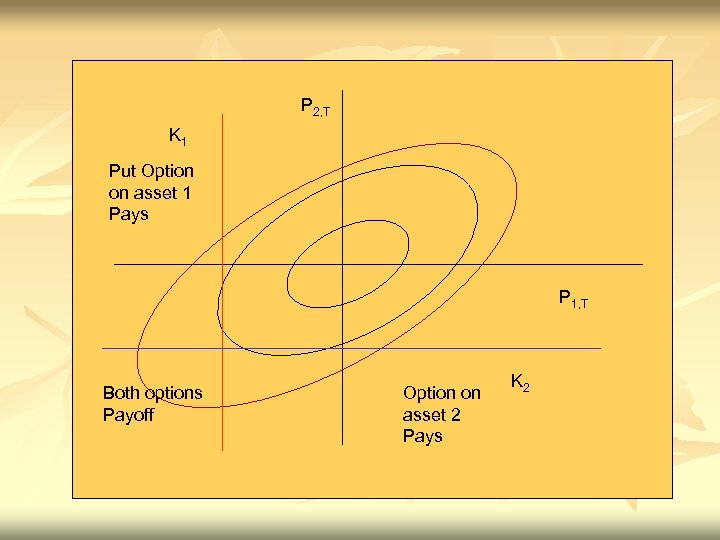P 2, T K 1 Put Option on asset 1 Pays P 1, T Both options Payoff Option on asset 2 Pays K 2

TWO PERIOD RETURNS n n n Two period return is the sum of two one period continuously compounded returns Look at binomial tree version Asymmetry gives negative skewness Low variance High variance

Two period Joint Returns n n If returns are both negative in the first period, then correlations are higher. This leads to lower tail dependence Up Market Down Market

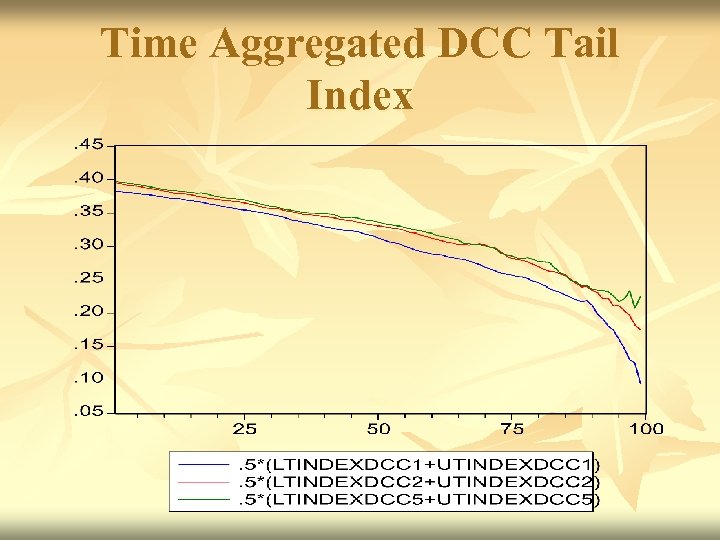Time Aggregated DCC Tail Index

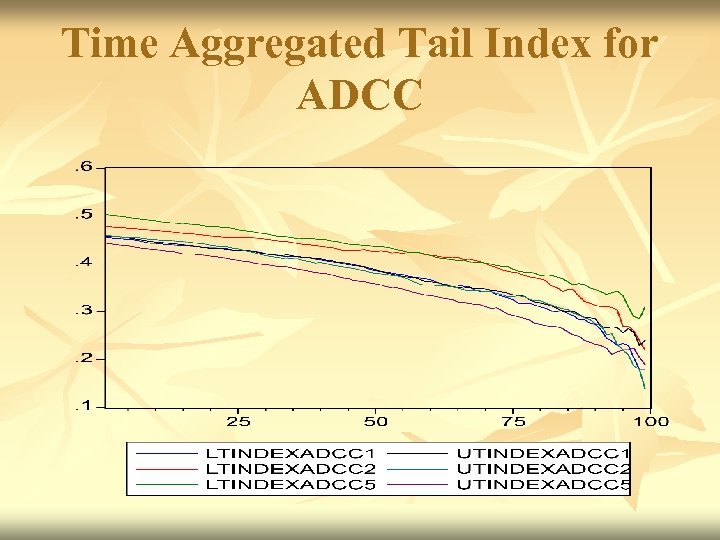Time Aggregated Tail Index for ADCC

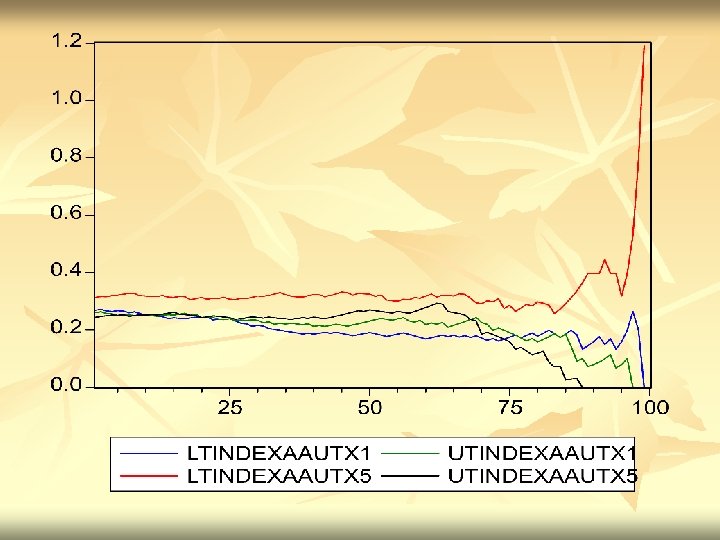
SOME RESULTS FOR EQUITY RETURNS – DOW STOCKS n n For 1992 -2002 take 10 years of equity returns from the 30 current Dow Jones Stocks. Calculate Tail correlations and Tail indexes for several pairs and their time aggregates.

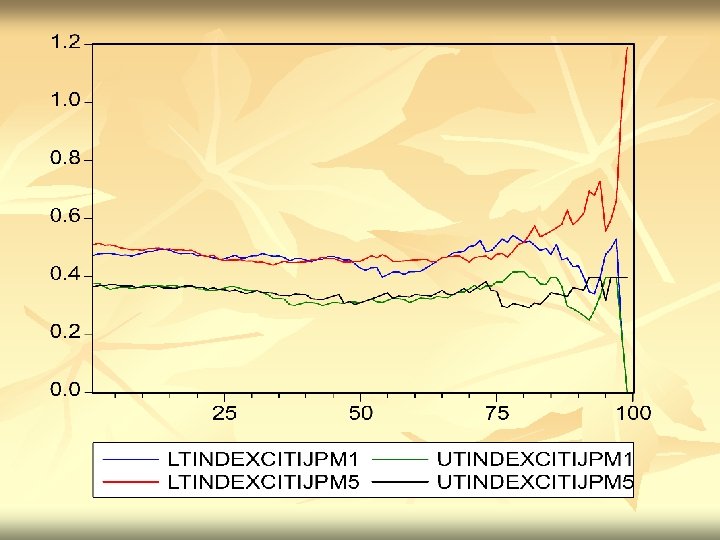
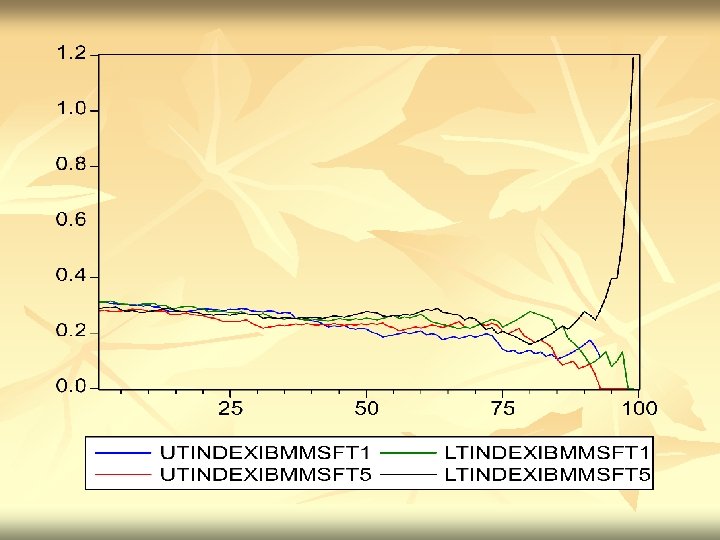
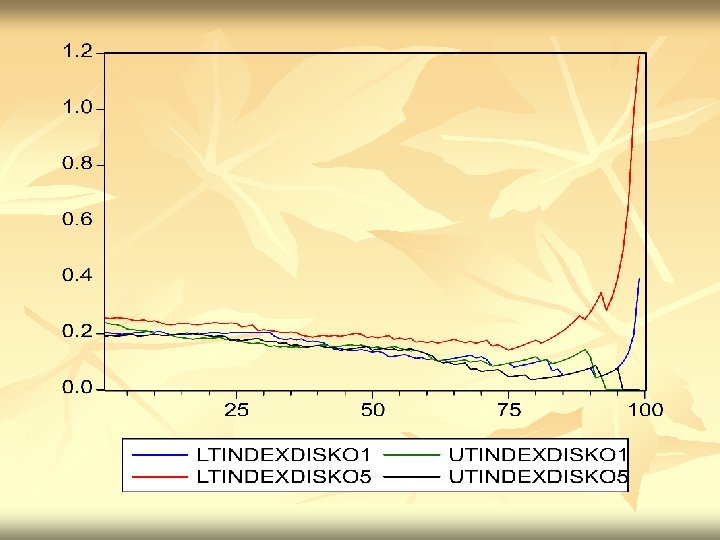
FINDINGS n n n DCC PROVIDES A FLEXIBLE APPROACH TO CORRELATION ESTIMATION ASYMPTOTIC STANDARD ERRORS CAN BE CONSTRUCTED FOR THE TWO AND THREE STEP ESTIMATORS TIME AGGREGATED SIMULATED ADCC AND REAL DATA SHOW HIGHER TAIL DEPENDENCE, PARTICULARLY IN LOWER TAIL

Data n n n Weekly $ returns Jan 1987 to Feb 2002 (785 observations) 21 Country Equity Series from FTSE All. World Index 13 Datastream Benchmark Bond Indices with 5 years average maturity

Europe AUSTRIA* BELGIUM* DENMARK* FRANCE* GERMANY* IRELAND* ITALY THE NETHERLANDS* SPAIN SWEDEN* SWITZERLAND* NORWAY UNITED KINGDOM* Australasia AUSTRALIA HONG KONG JAPAN* NEW ZEALAND SINGAPORE Americas CANADA* MEXICO UNITED STATES*

GARCH Models (asymmetric in orange) n n n n n GARCH AVGARCH NGARCH EGARCH ZGARCH GJR-GARCH APARCH AGARCH NAGARCH n n n n n 3 EQ, 8 BOND 0 1 BOND 6 EQ, 1 BOND 8 EQ, 1 BOND 3 EQ, 1 BOND 0 1 EQ, 1 BOND 0

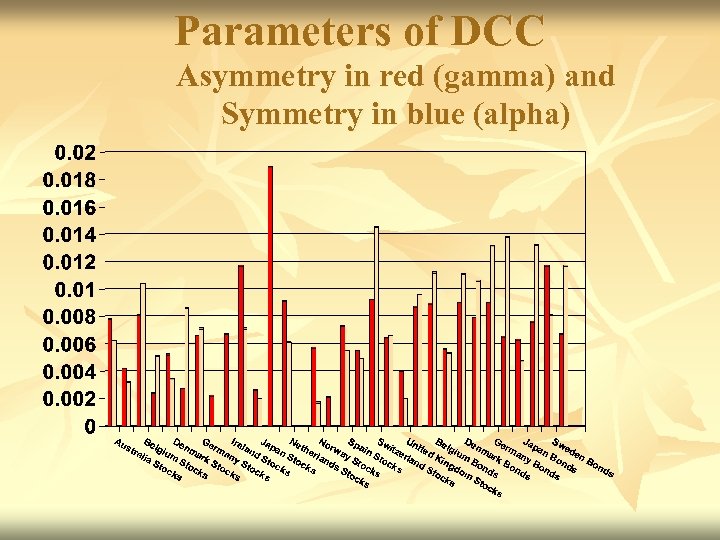Parameters of DCC Asymmetry in red (gamma) and Symmetry in blue (alpha)

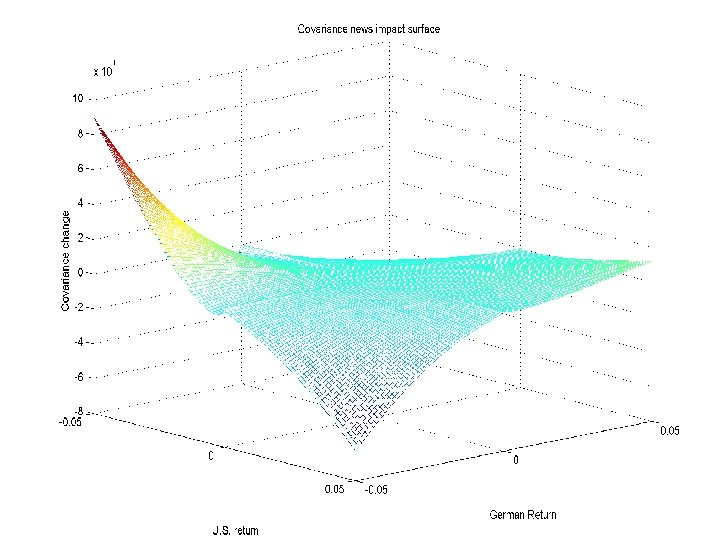
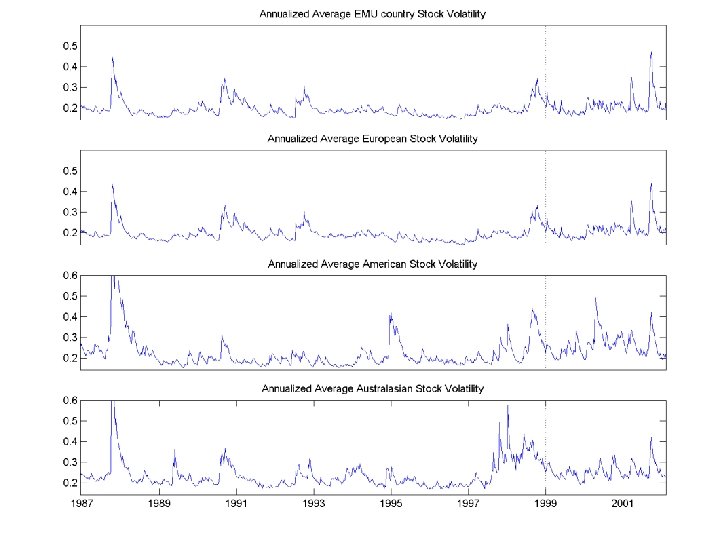
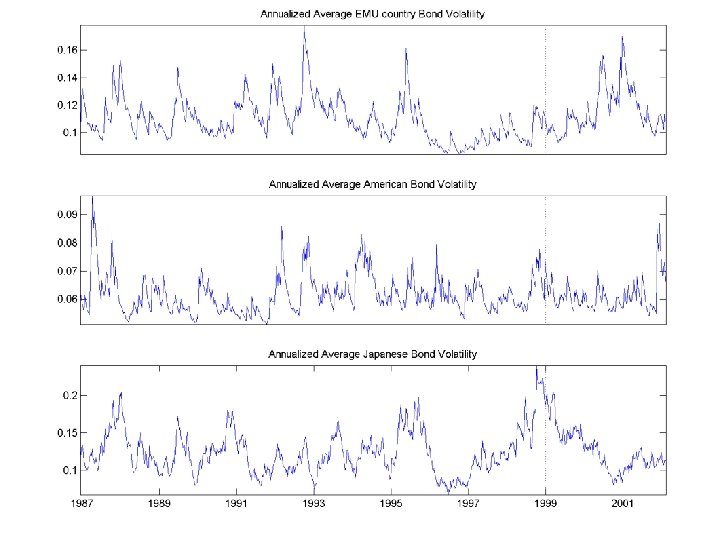
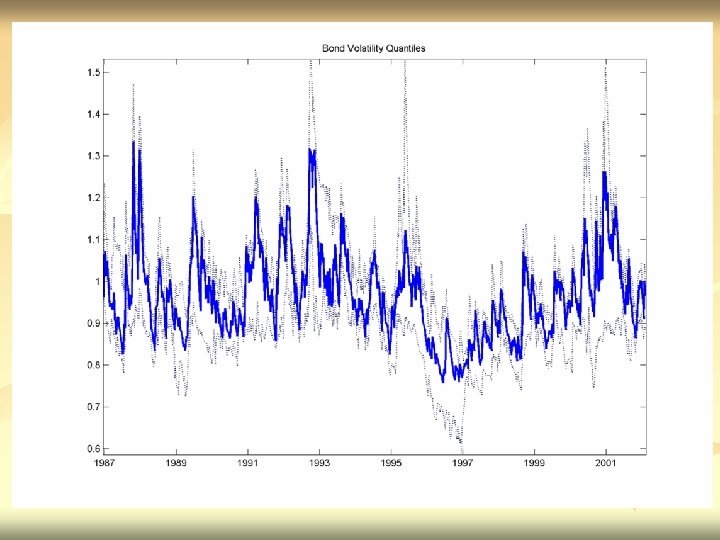
CORRELATIONS OF VOLATILITIES n EQUITIES =. 32 n n EUROPEAN =. 55 BONDS =. 35 n WITHIN EMU =. 79

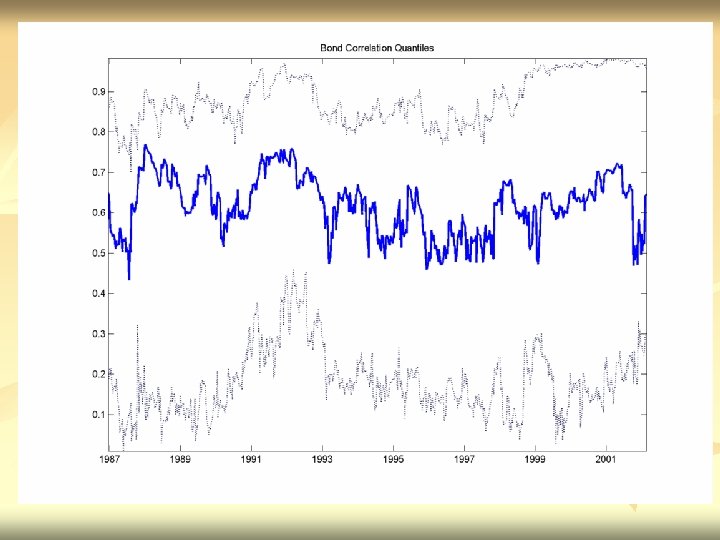
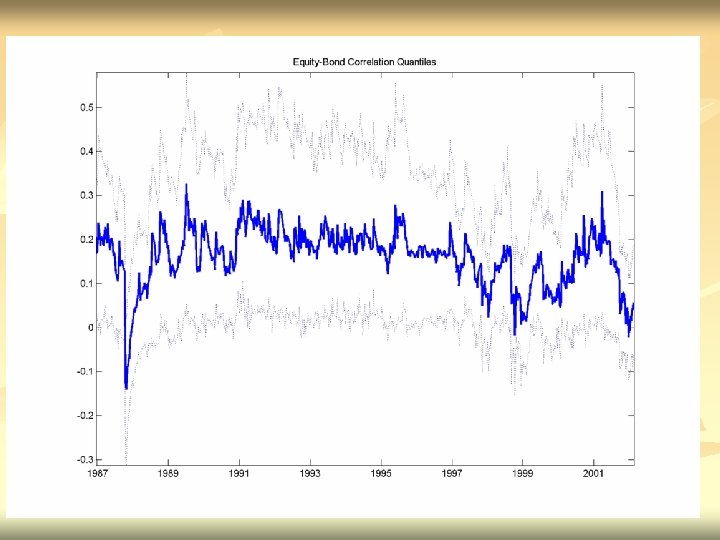
BEHAVIOR DURING US BEAR MARKETS

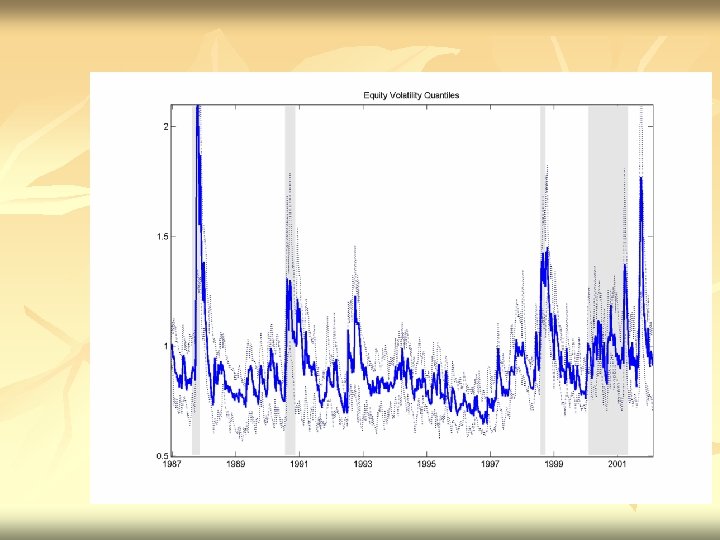
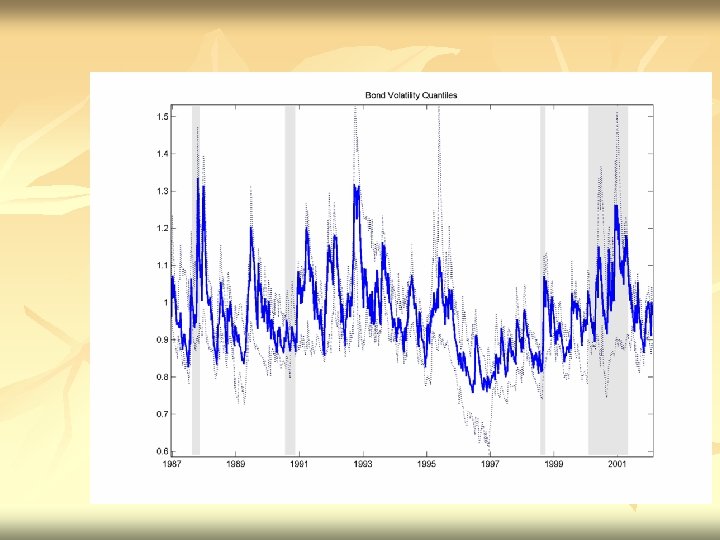
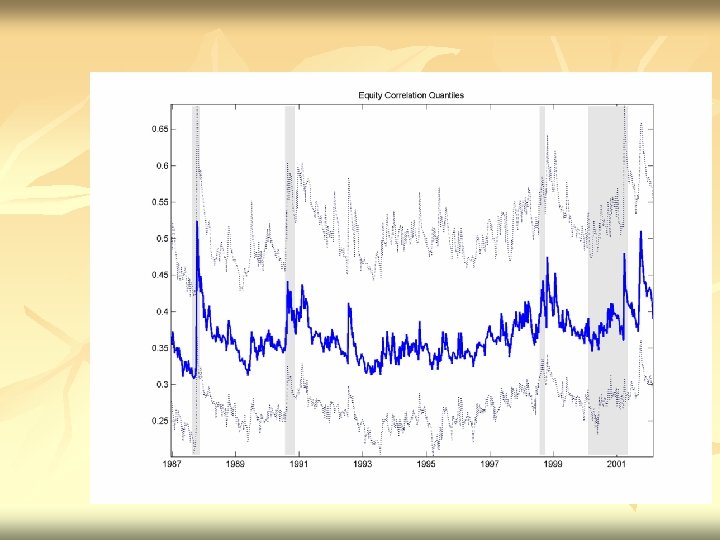
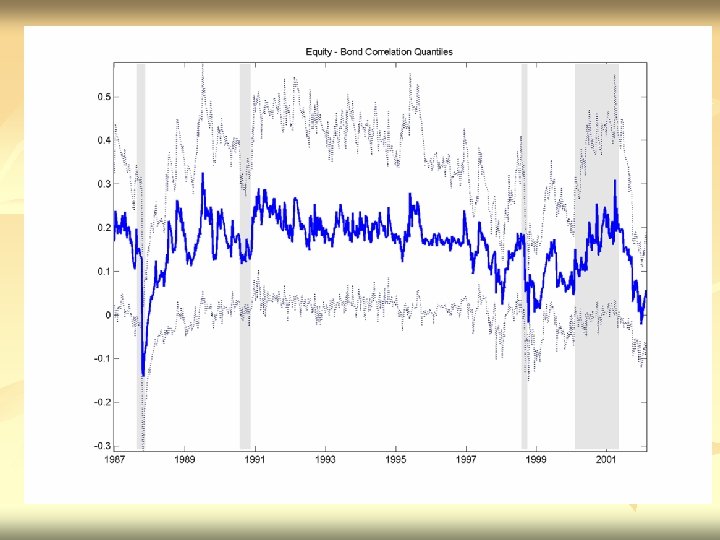
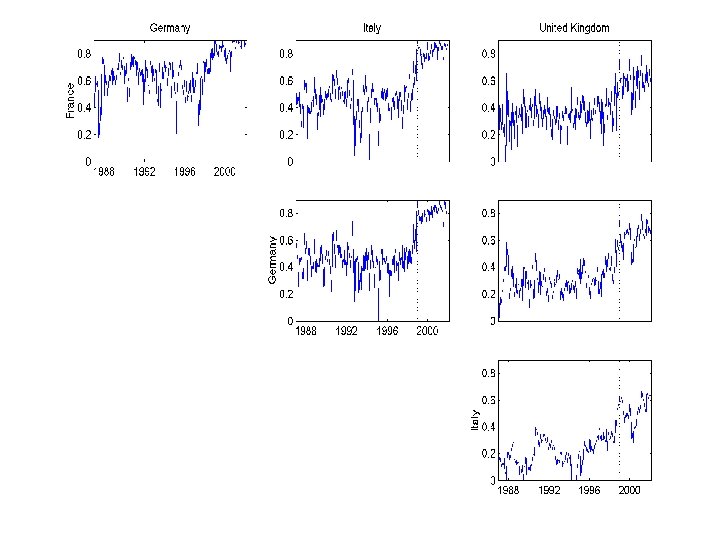
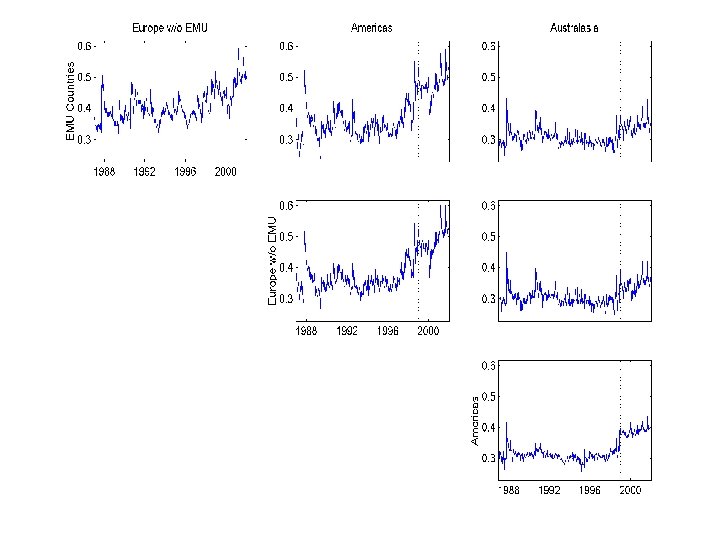
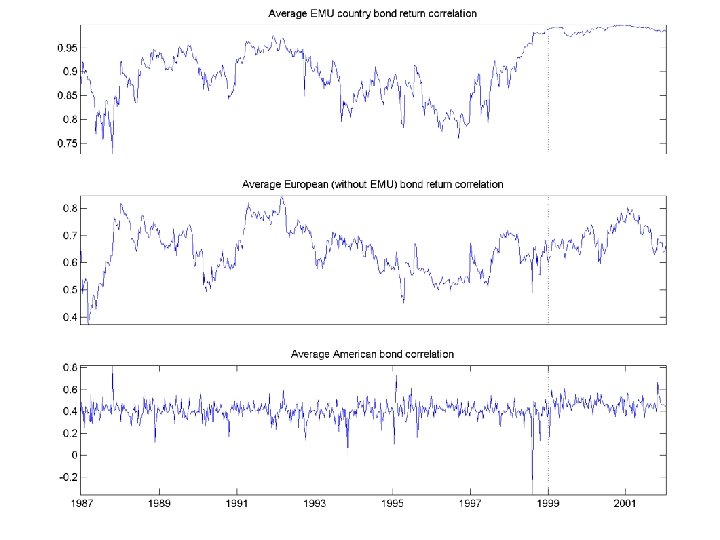
RESULTS n n Asymmetric Correlations – correlations rise in down markets Shift in level of correlations with formation of Euro Equity Correlations are rising not just within EMU-Globalization? EMU Bond correlations are especially highothers are also rising