Двойной интеграл Вычисление двойного интеграла Рыбникова Екатерина Группа Э(БУ)-14 -1
Вычисление двойного интеграла Пусть требуется вычислить двойной интеграл , где функция непрерывна в области. Тогда двойной интеграл выражает объем цилиндрического тела, ограниченного сверху поверхностью. Найдем этот объем, используя метод параллельных сечений. Ранее было показано, что где – площадь сечения плоскостью, перпендикулярной оси Ox, а – уравнение плоскостей, ограничивающих данное тело. 2
Вычисление двойного интеграла Положим сначала, что область D представляет собой криволинейную трапецию, ограниченную прямыми и кривыми , причем функции непрерывны и таковы, что для всех. Такая область называется правильной в направлении оси Оу: любая прямая, параллельная оси Оу, пересекает границу области не более чем вы двух точках. 3
Вычисление двойного интеграла Построим сечение цилиндрического тела плоскостью, перпендикулярной оси Ох: , где. В сечении получим криволинейную трапецию ABCD, ограниченную линиями , где , 4
Вычисление двойного интеграла Площадь этой трапеции находим с помощью определенного интеграла Теперь, согласно методу параллельных сечений, искомый объем цилиндрического тела может быть найден так: 5
Вычисление двойного интеграла С другой стороны, 6
Двукратный интеграл Это равенство обычно записывается в виде (3) Формула (1) представляет собой способ вычисления двойного интеграла в декартовых координатах. Правую часть формулы (3) называют двукратным (или повторным) интегралом от функции по области D. При этом называется внутренним интегралом. 7
Двукратный интеграл Для вычисление двукратного интеграла сначала берем внутренний интеграл, считая постоянным, затем берем внешний интеграл, т. е результат первого интегрирования интегрируем по х в пределах от а до b. Если же область D ограничена прямыми , кривыми , причем для всех , т. е область D – правильная в направлении оси Ох, то, рассекая тело плоскостью , аналогично получим: (4) Здесь, при вычислении внутреннего интеграла, считаем y постоянным. 8
Замечания 1. Формулы (3) и (4) справедливы и в том случае, когда. 2. Если область правильна в обоих направлениях, то двойной интеграл можно вычислять как по формуле (3), так и по формуле (4). 3. Если область не является правильной ни «по х» , ни «по у» , то для сведения двойного интеграла к повторным ее следует разбить на части, правильные в направлении оси Ох или оси Оу. 4. Полезно помнить, что внешние пределы в двухкратном интеграле всегда постоянны, а внутренние, как правило, переменные. 9
Повторный интеграл 1) Если 2) Границы интегрирования по x не зависят от у 3) Границы интегрирования по y не зависят от x (5) Выражение (5) называется повторным интегралом.
Пример 1 Вычислить , где область ограничена линиями 11
Пример 1 Решение: На рисунке (слайд 10) изображена область интегрирования. Она правильная в направлении оси Ox. Для вычисления данного двойного интеграла воспользуемся формулой (4): 12
Пример 1 13
Отметим, что для вычисления данного двойного интеграла можно воспользоваться формулой (3). Но для этого область следует разбить на две области: . Получаем: 14
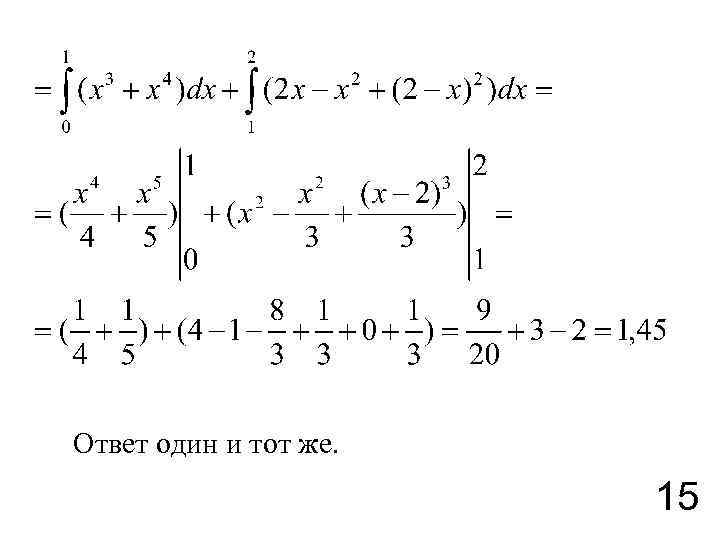
Ответ один и тот же. 15
Скачать презентацию Двойной интеграл Вычисление двойного интеграла Рыбникова Екатерина Группа
0_3.ppt