ДВОИЧНАЯ СИСТЕМА СЧИСЛЕНИЯ ДЕСЯТИЧНАЯ И ДВОИЧНАЯ СИСТЕМЫ

ДВОИЧНАЯ СИСТЕМА СЧИСЛЕНИЯ

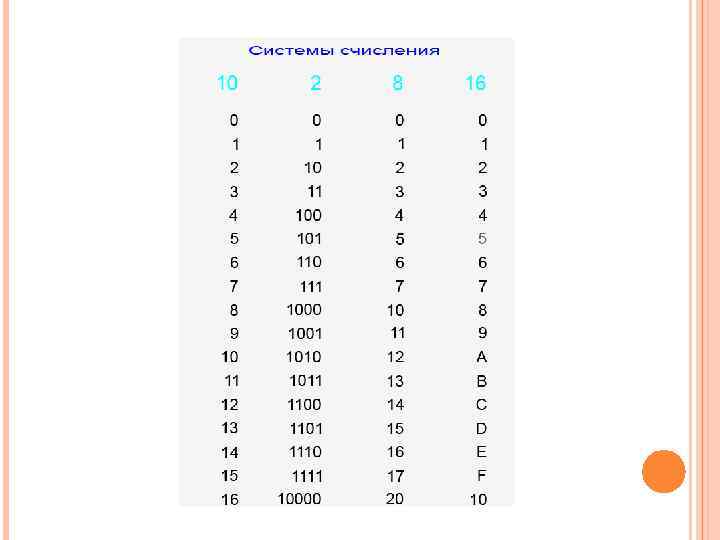
ДЕСЯТИЧНАЯ И ДВОИЧНАЯ СИСТЕМЫ СЧИСЛЕНИЯ Системой счисления называют правила записи чисел и связанные с ними способы выполнения вычислений. Компьютер работает с числами в двоичной системе счисления.

РАЗВЕРНУТАЯ ФОРМА ЗАПИСИ ЧИСЛА Цифра, которая является крайней справа, говорит нам о количестве единиц этого числа, следующая за этой цифрой, как правило, указывает на количество двоек и т. д. Если мы с вами, например, возьмем такое число, как 333, то увидим, что крайняя правая цифра обозначает три единицы, потом три десятка и за ней – три сотни. Теперь это изобразим в виде такого равенства:

Здесь мы видим равенство, в котором выражение, расположенное с правой стороны от знака равно, предоставлено в виде развернутой формы записи этого многозначного числа. Рассмотрим еще один пример многозначного десятичного числа, который также представлен в развернутой форме: Эти примеры нам показывают, что чем дальше мы движемся от цифры к цифре справа налево, то каждая цифра увеличивается в десять раз. А происходит это потому, что основание системы счисления равно десяти.

ПЕРЕВОД ДВОИЧНЫХ ЧИСЕЛ В ДЕСЯТИЧНУЮ СИСТЕМУ Для примера возьмем такое многозначительное двоичное число, как: В этом многозначительном числе мы видим с правой стороны внизу двойку, которая нам указывает на основание системы счисления. То есть, нам понятно, что перед нами двоичное число и перепутать его с десятичным, мы уже не можем. И значение каждой следующей цифры в двоичном числе возрастает в 2 раза при каждом шаге справа налево. Теперь давайте посмотрим, как будет выглядеть развернутая форма записи этого двоичного числа:

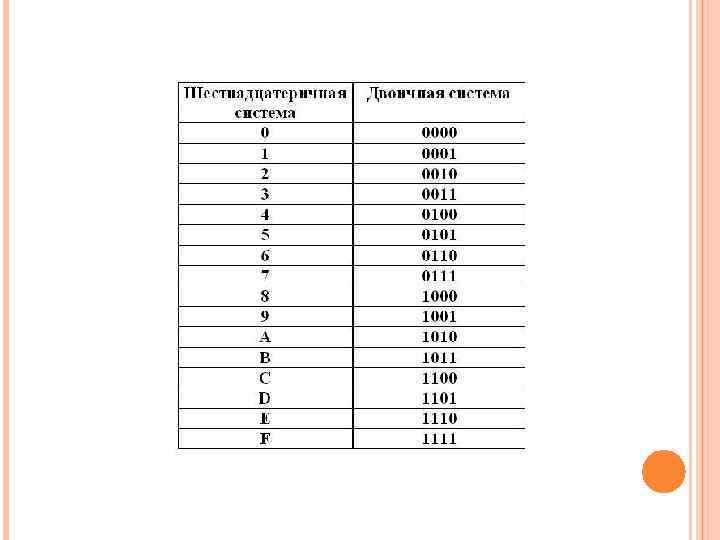
ПЕРЕВОД ДЕСЯТИЧНЫХ ЧИСЕЛ В ДВОИЧНУЮ СИСТЕМУ Для такого перевода необходимо попробовать разложить десятичное число на слагаемые, которые представляют собой степени двойки. Приведем такой пример:

Теперь рассмотрим методы записи деления на число два. Для примера возьмем число 37 и попробуем его перевести в двоичную систему. На данных примерах мы видим, что а 5, а 4, а 3, а 2, а 1, а 0 являются обозначением цифр в записи двоичного числа, которые осуществляются по порядку слева направо. В итоге мы с вами получим:

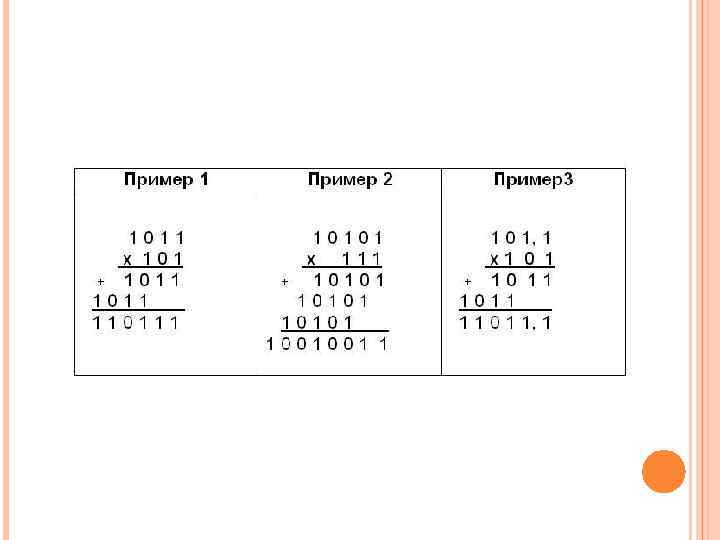
АРИФМЕТИКА ДВОИЧНЫХ ЧИСЕЛ Если исходить из правил в арифметике, то легко заметить, что в двоичной системе счислений, они намного проще, чем в десятичной. Теперь давайте вспомним варианты сложения и умножения однозначных двоичных чисел. Благодаря такой простоте, которая легко согласовывается с битовой структурой компьютерной памяти, двоичная система счисления привлекла внимание создателей компьютера.

КОРОТКО О ГЛАВНОМ Система счисления — определенные правила записи чисел и связанные с этими правилами способы выполнения вычислений. Основание системы счисления равно количеству используемых в ней цифр. Двоичные числа — числа в двоичной системе счисления. В их записи используются две цифры: 0 и 1. Развернутая форма записи двоичного числа — это его представление в виде суммы степеней двойки, умноженных на 0 или на 1. Использование двоичных чисел в компьютере связано с битовой структурой компьютерной памяти и простотой двоичной арифметики.

ДОСТОИНСТВА ДВОИЧНОЙ СИСТЕМЫ СЧИСЛЕНИЯ Во-первых, достоинством двоичной системы счисления является то, что с ее помощью довольно таки просто осуществлять процессы хранения, передачи и обработки информации на компьютере. Во-вторых, для ее выполнения достаточно не десять элементов, а лишь два; В-третьих, отображение информации с помощью лишь двух состояний, это надежнее и более устойчиво к различным помехам; В-четвертых, есть возможность использования алгебры логики для осуществления логических преобразований; В-пятых, двоичная арифметика все же проще десятичной, поэтому является более удобной.

НЕДОСТАТКИ ДВОИЧНОЙ СИСТЕМЫ СЧИСЛЕНИЯ Двоичная система счисления менее удобна, так как человек привык больше пользоваться десятичной системой, которая намного короче. А вот, в двоичной системе большие числа имеет довольно таки большое число разрядов, что и является ее существенным недостатком.