Движение жидкости в трубах Гидравлические сопротивления Определение потерь

Движение жидкости в трубах. Гидравлические сопротивления. Определение потерь напора на трение. Местные сопротивления Лекция 9

1 Ламинарный режим движения жидкости это 1. режим, при котором частицы жидкости перемещаются бессистемно только у стенок трубопровода; 2. режим, при котором частицы жидкости в трубопроводе перемещаются бессистемно; 3. режим, при котором жидкость движется послойно; 4. режим, при котором частицы жидкости двигаются послойно только у стенок трубопровода. 2 Скорость движения жидкости максимальна при ламинарном режиме 1. у стенок трубопровода; 2. в центре трубопровода; 3. может быть максимальна в любом месте; 4. в начале трубопровода. 3 Число Рейнольдса 1. Re=υd/μ 2. Re=υd/v 3. Re=vd/υ 4. Re=vl/υ 4 Средняя скорость жидкости в трубе круглого сечения с гидравлическим радиусом 0, 5 м при расходе 2 м 3/с составляет _____ м/с 1. 0, 636 2. 6, 36 3. 0, 0636 4. 0, 318 5 Критическое значение числа Рейнольдса равно 1. 580 2. 2300; 2. 3200; 3. 4000; 4. 4600.

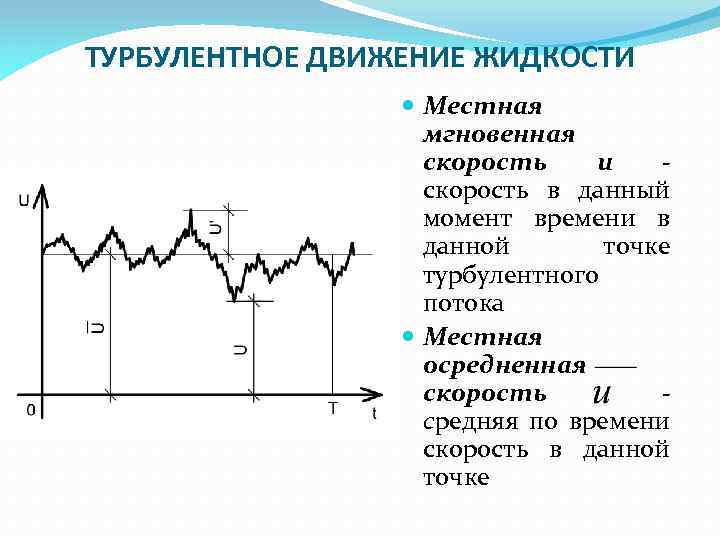
ТУРБУЛЕНТНОЕ ДВИЖЕНИЕ ЖИДКОСТИ Местная мгновенная скорость u скорость в данный момент времени в данной точке турбулентного потока Местная осредненная скорость средняя по времени скорость в данной точке

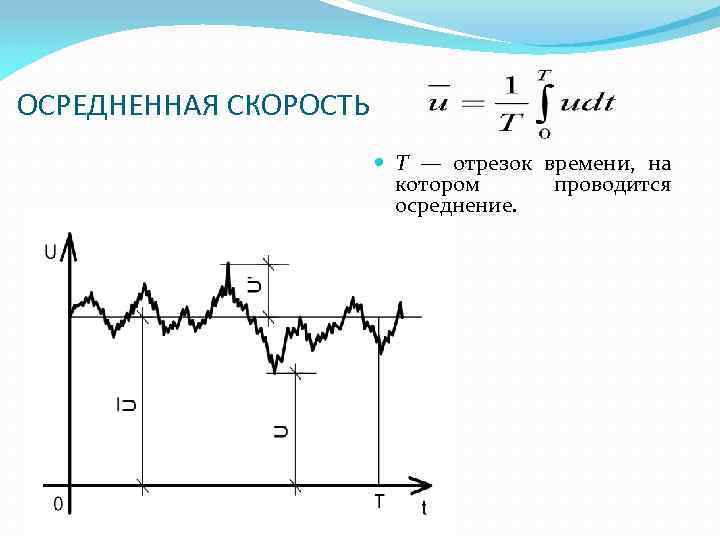
ОСРЕДНЕННАЯ СКОРОСТЬ Т — отрезок времени, на котором проводится осреднение.

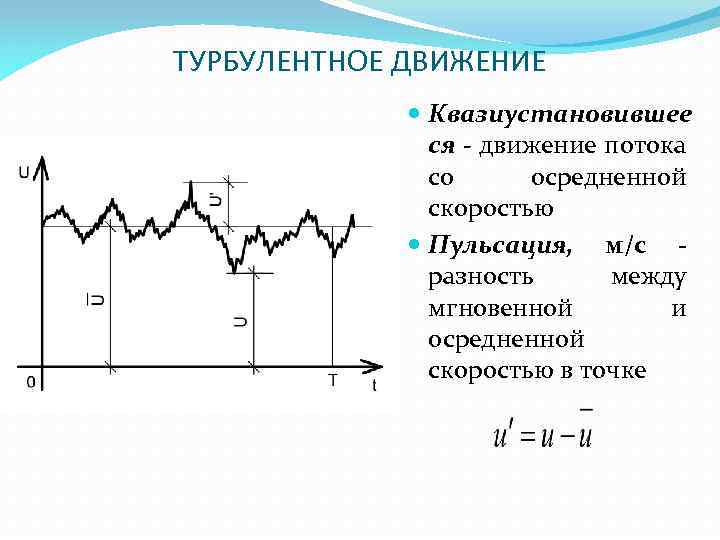
ТУРБУЛЕНТНОЕ ДВИЖЕНИЕ Квазиустановившее ся - движение потока со осредненной скоростью Пульсация, м/с разность между мгновенной и осредненной скоростью в точке

ТУРБУЛЕНТНОЕ ДВИЖЕНИЕ Касательное напряжение обусловлено турбулентным перемешиванием (инерционные силы) и сцеплением (силы внутреннего трения), Па Если ось ox направить вдоль движения, то – турбулентная вязкость, Па с μ – динамическая вязкость, Па с.

ТУРБУЛЕНТНОЕ ДВИЖЕНИЕ При больших числах Рейнольдса вязкостные силы незначительны по сравнению с инерционными При меньшей степени турбулентности величина динамической вязкости соизмерима с турбулентной вязкостью и при определении потерь напора необходимо учитывать как вязкостные, так и инерционные силы

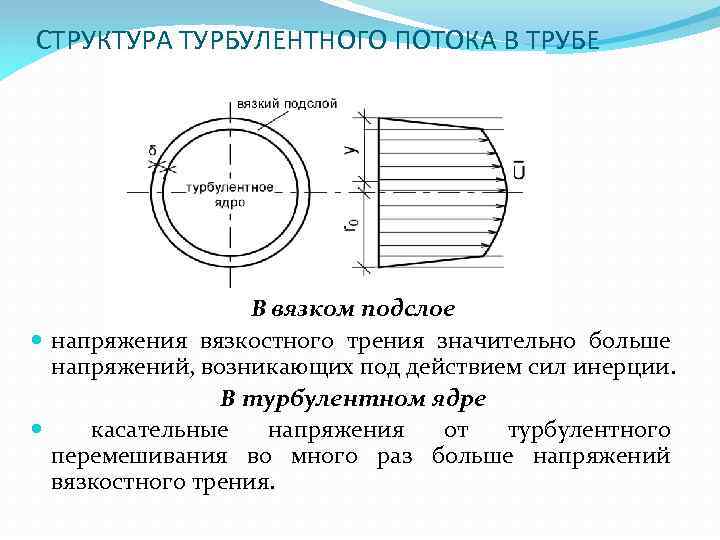
СТРУКТУРА ТУРБУЛЕНТНОГО ПОТОКА В ТРУБЕ В вязком подслое напряжения вязкостного трения значительно больше напряжений, возникающих под действием сил инерции. В турбулентном ядре касательные напряжения от турбулентного перемешивания во много раз больше напряжений вязкостного трения.

РАСПРЕДЕЛЕНИЕ ОСРЕДНЕННЫХ СКОРОСТЕЙ ПО СЕЧЕНИЮ Для вязкого подслоя делается допущение, что в его пределах касательные напряжения τ0= const – динамическая скорость, м/с; у — расстояние точки от стенки трубы, м; γ – кинематическая вязкость, м 2/с

РАСПРЕДЕЛЕНИЕ ОСРЕДНЕННЫХ СКОРОСТЕЙ ПО СЕЧЕНИЮ Для турбулентного ядра продольные и поперечные пульсации пропорциональны расстоянию от стенки и градиенту осредненной скорости χ=0, 4 – постоянная Никурадзе;

РАСПРЕДЕЛЕНИЕ ОСРЕДНЕННЫХСКОРОСТЕЙ ПО СЕЧЕНИЮ При ламинарном движении - параболический закон изменения местных скоростей по сечению. При турбулентном движении - логарифмический закон. Отношение максимальной осредненной скорости к средней по сечению для турбулентного движения 1, 15— 1, 3, для ламинарного движения 2.

ВЯЗКИЙ ПОДСЛОЙ, ЭКВИВАЛЕНТНАЯ ШЕРОХОВАТОСТЬ δ - толщина вязкого подслоя, м d – диаметр, м Re – число Рейнольдса λ – коэффициент Дарси Эквивалентная шероховатость Δэкв такая равномерная шероховатость, которая дает при подсчете одинаковую с заданной шероховатостью величину гидравлического коэффициента трения λ.

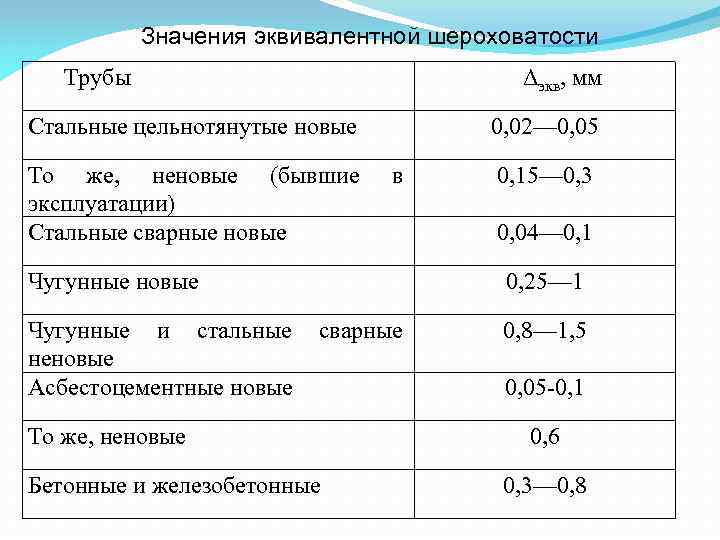
Значения эквивалентной шероховатости Трубы Δэкв, мм Стальные цельнотянутые новые То же, неновые (бывшие эксплуатации) Стальные сварные новые 0, 02— 0, 05 в Чугунные новые Чугунные и стальные неновые Асбестоцементные новые 0, 15— 0, 3 0, 04— 0, 1 0, 25— 1 сварные То же, неновые Бетонные и железобетонные 0, 8— 1, 5 0, 05 -0, 1 0, 6 0, 3— 0, 8

ЗОНА ГИДРАВЛИЧЕСКИ ГЛАДКИХ ТРУБ Δэкв < δ < 10 Шероховатость не влияет на гидравлические сопротивления и гидравлический коэффициент трения, который зависит только от числа Рейнольдса. Формула Блазиуса С учетом зависимостей и , потери напора пропорциональны скорости в степени 1, 75. kгл– коэффициент пропорциональности

ПЕРЕХОДНАЯ ЗОНА Δэкв = δ 10 < <500 На гидравлическое сопротивление влияют как число Рейнольдса, так и величина выступов шероховатости Формула Альтшуля

ЗОНА ШЕРОХОВАТОГО ТРЕНИЯ Δэкв>δ >500 Формула Шифринсона Потери напора скорости пропорциональны квадрату

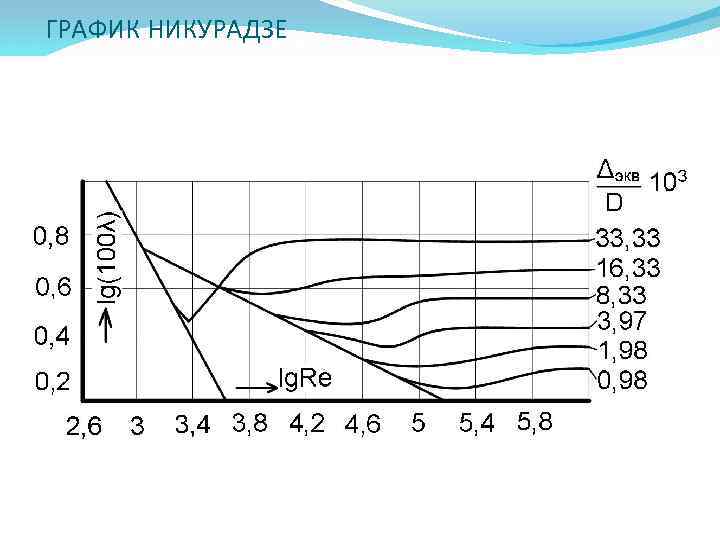
ГРАФИК НИКУРАДЗЕ

ГИДРАВЛИЧЕСКИЙ КОЭФФИЦИЕНТ ТРЕНИЯ При ламинарном режиме λ зависит только от числа Рейнольдса. При значениях Re = 2320 -4000 в зоне периодической смены режимов λ быстро растет. В области гидравлически гладких труб λ зависит только от числа Рейнольдса, уменьшаясь с увеличением последнего. В переходной области значения λ в общем возрастают с ростом числа Рейнольдса Rе, но для малых шероховатостей на начальном участке имеет место спад. В области гидравлически шероховатых труб коэффициент λ представлен семейством горизонтальных прямых, разных для различных шероховатостей.

Гидравлический коэффициент трения Асбестоцементные трубы обычно работают в переходной области сопротивления. Неновые стальные и чугунные трубы при скоростях движения воды V<1, 2 м/с работают в переходной области сопротивления, а при V>1, 2 м/с — в области гидравлически шероховатых труб. Ф. А. Шевелевым составлены таблицы по определению потерь напора в водопроводных трубах на основании эмпирических формул Для расчета движения сточных вод в водоотводных (канализационных) напорных и безнапорных трубах применяется формула Н. Федорова. Для расчета потерь в канализационных трубах также имеются таблицы Лукиных.

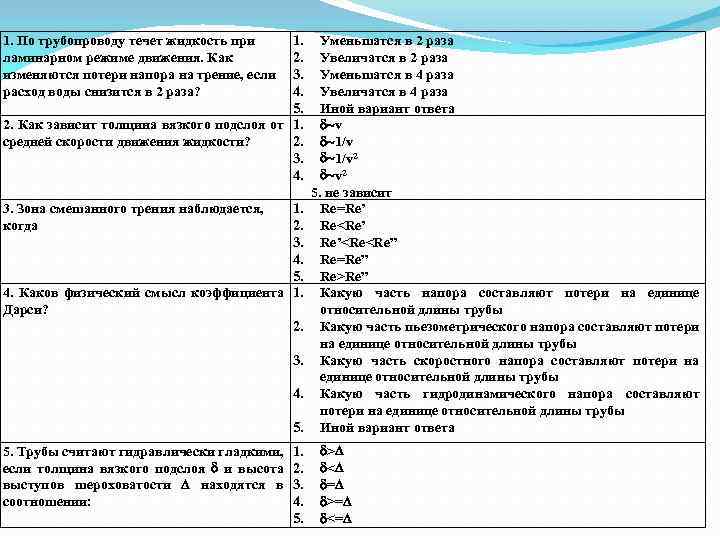
1. 2. 3. 4. 5. 2. Как зависит толщина вязкого подслоя от 1. средней скорости движения жидкости? 2. 3. 4. 1. По трубопроводу течет жидкость при ламинарном режиме движения. Как изменяются потери напора на трение, если расход воды снизится в 2 раза? 1. 2. 3. 4. 5. 4. Каков физический смысл коэффициента 1. Дарси? 2. 3. Зона смешанного трения наблюдается, когда 3. 4. 5. 5. Трубы считают гидравлически гладкими, если толщина вязкого подслоя и высота выступов шероховатости находятся в соотношении: 1. 2. 3. 4. 5. Уменьшатся в 2 раза Увеличатся в 2 раза Уменьшатся в 4 раза Увеличатся в 4 раза Иной вариант ответа v 1/v 2 5. не зависит Re=Re’ Re<Re’ Re’<Re<Re” Re=Re” Re>Re” Какую часть напора составляют потери на единице относительной длины трубы Какую часть пьезометрического напора составляют потери на единице относительной длины трубы Какую часть скоростного напора составляют потери на единице относительной длины трубы Какую часть гидродинамического напора составляют потери на единице относительной длины трубы Иной вариант ответа > < = >= <=

МЕСТНЫЕ СОПРОТИВЛЕНИЯ резкое изменение конфигурации живого сечения потока, течение с изменением скорости, поперечная циркуляция на изгибе потока, соединение и разделение потоков Местные сопротивления делятся на простые и сложные

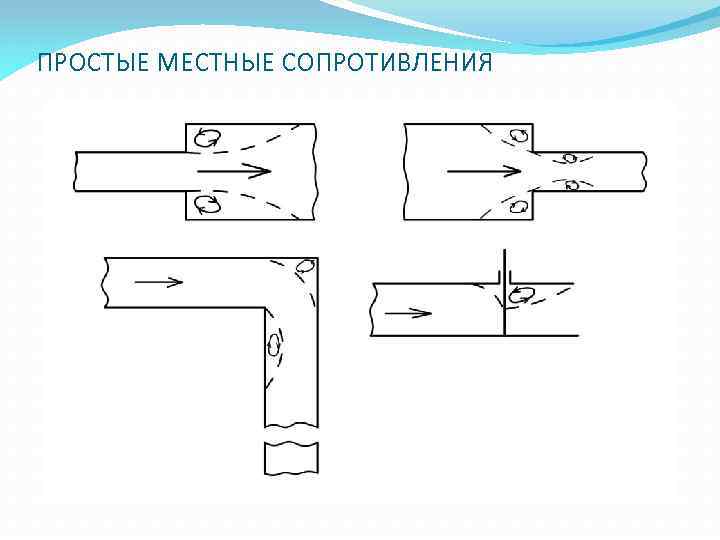
ПРОСТЫЕ МЕСТНЫЕ СОПРОТИВЛЕНИЯ

ПРОСТЫЕ МЕСТНЫЕ СОПРОТИВЛЕНИЯ При обтекании углов или элементов арматуры за ними возникают водоворотные зоны, на поддержание течений, в которых расходуется напор (энергия) Между транзитным потоком и водоворотными зонами возникают поверхности раздела Одни массы жидкости в водоворотных зонах заменяются другими, но в целом это явление является установившимся Течение отрывное

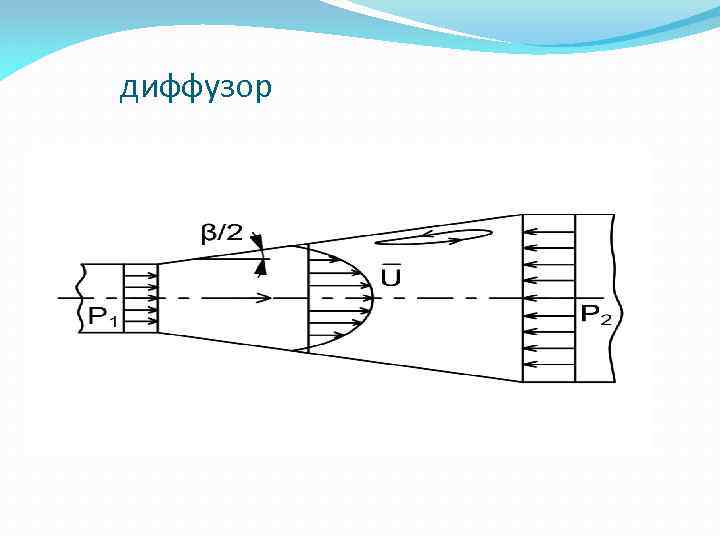
диффузор

диффузор Противодавление затрудняет поступательное движение жидкости, особенно у стенок, где скорости имеют небольшие значения. При углах расширения β>8 -10° частицы у стенок могут остановиться и даже начать двигаться назад, что приводит к отрыву основного потока от стенки и образованию водоворотных зон. Во избежание больших потерь напора рекомендуется выполнять расширения трубы с углом β< 8°.

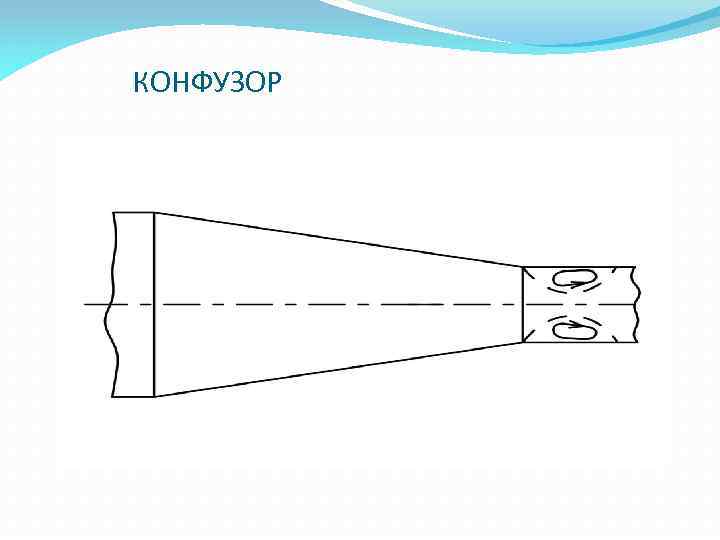
КОНФУЗОР

КОНФУЗОР Разность давлений способствует движению. Потери напора на конфузорах меньше потерь на диффузорах Происходит переформирования скоростной структуры потока при сужении, а также обтекании угла при выходе из конфузора

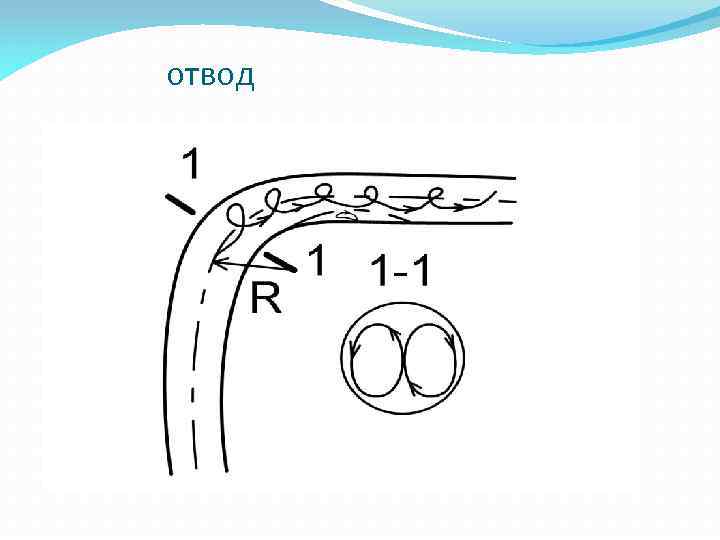
отвод

отвод Возникают центробежные силы, которые увеличивают давление у вогнутой стенки и уменьшают у выпуклой. Поперечная циркуляция – вращательнопоступательное движение от области большего давления к области меньшего давления.

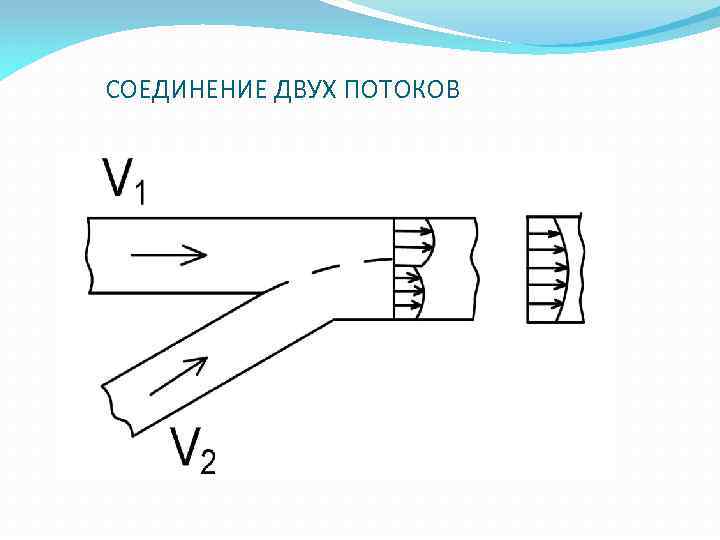
СОЕДИНЕНИЕ ДВУХ ПОТОКОВ

СОЕДИНЕНИЕ ДВУХ ПОТОКОВ Возникает поверхность раздела изза разных скоростей частиц жидкости по обе стороны от нее Потери энергии обусловливаются ее затратами на переформирование кинематической структуры потока

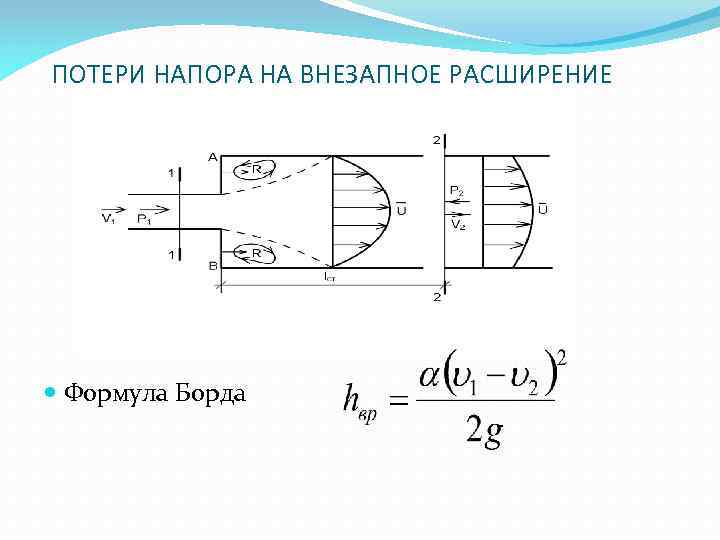
ПОТЕРИ НАПОРА НА ВНЕЗАПНОЕ РАСШИРЕНИЕ Формула Борда

ФОРМУЛА ВЕЙСБАХА ДЛЯ ОПРЕДЕЛЕНИЯ МЕСТНЫХ ПОТЕРЬ НАПОРА , м, где ξ — коэффициент местных сопротивлений, определяемый, как правило, опытным путем υ – скорость, м/с. Скоростной напор вычисляется, если нет особой оговорки, по скорости за сопротивлением.

Каждое местное сопротивление деформирует поток, увеличивает пульсацию и приводит к перераспределению осредненных скоростей по сечению. Коэффициент кинетической энергии α непосредственно за сопротивлением больше, чем при равномерном движении В связи с разностью коэффициентов кинетической энергии в начале и конце участка стабилизации их следует включать в величину местных потерь.

Коэффициент сопротивления при внезапном расширении Потери на выходе из трубы в резервуар под уровень могут быть определены из предположения, что размеры резервуара значительно больше диаметра трубы. Тогда, считая в формуле V 2 = 0, получим Коэффициент сопротивления при внезапном сужении по формуле Идельчика Вход из резервуара в трубу как резкое сужение от очень большого диаметра к очень малому (d 2 <d 1). Тогда d 2 ~ 0, получим, что ξ вх = 0, 5.

ЛАМИНАРНЫЙ РЕЖИМ При малых числах Рейнольдса ξкв— коэффициент рассматриваемого местного сопротивления для квадратичного режима; В — коэффициент, определяемый для разных местных сопротивлений

СЛОЖНЫЕ СОПРОТИВЛЕНИЯ Принцип наложения потерь: при наличии в трубопроводе нескольких местных сопротивлений потери напора на них складываются Расстояние, на котором сказывается взаимное влияние местных сопротивлений, определяется по формуле А. Д. Альтшуля При расстояниях между сопротивлениями l< lвл потери напора на первом сопротивлении еще не полностью проявляются, а потери на втором сопротивлении уже начинают сказываться. Общие потери напора на двух сопротивлениях меньше суммы потерь на этих двух сопротивлениях

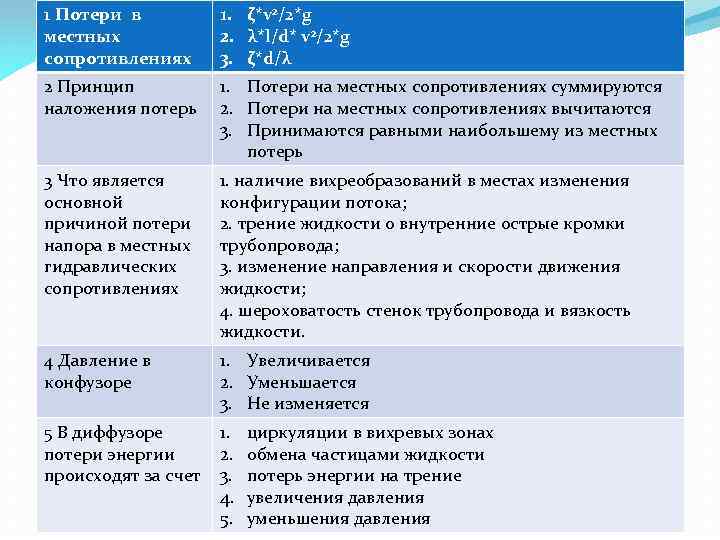
1 Потери в местных сопротивлениях 1. ζ*v 2/2*g 2. λ*l/d* v 2/2*g 3. ζ*d/λ 2 Принцип наложения потерь 1. Потери на местных сопротивлениях суммируются 2. Потери на местных сопротивлениях вычитаются 3. Принимаются равными наибольшему из местных потерь 3 Что является основной причиной потери напора в местных гидравлических сопротивлениях 1. наличие вихреобразований в местах изменения конфигурации потока; 2. трение жидкости о внутренние острые кромки трубопровода; 3. изменение направления и скорости движения жидкости; 4. шероховатость стенок трубопровода и вязкость жидкости. 4 Давление в конфузоре 1. Увеличивается 2. Уменьшается 3. Не изменяется 5 В диффузоре потери энергии происходят за счет 1. 2. 3. 4. 5. циркуляции в вихревых зонах обмена частицами жидкости потерь энергии на трение увеличения давления уменьшения давления

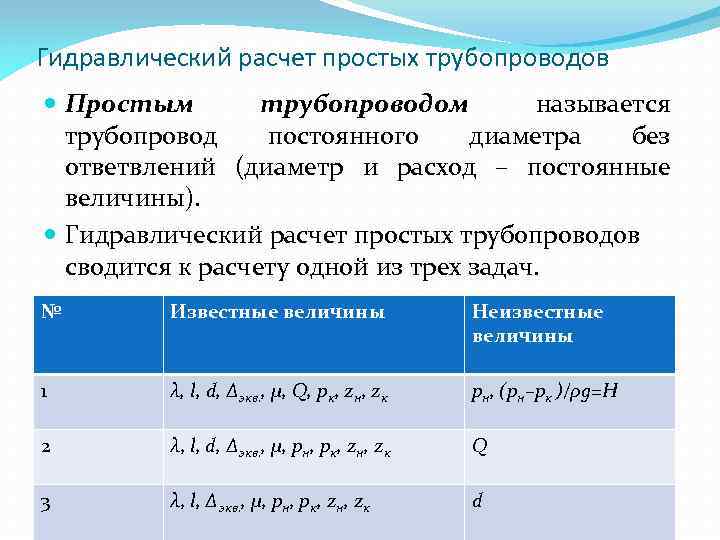
Гидравлический расчет простых трубопроводов Простым трубопроводом называется трубопровод постоянного диаметра без ответвлений (диаметр и расход – постоянные величины). Гидравлический расчет простых трубопроводов сводится к расчету одной из трех задач. № Известные величины Неизвестные величины 1 λ, l, d, ∆экв. , μ, Q, pк, zн, zк pн, (pн–pк )/ρg=H 2 λ, l, d, ∆экв. , μ, pн, pк, zн, zк Q 3 λ, l, ∆экв. , μ, pн, pк, zн, zк d

ОСНОВНЫЕ РАСЧЕТНЫЕ ФОРМУЛЫ 1) уравнение Бернулли 2) уравнение неразрывности 3) потери напора между начальным и конечным сечениями 4) потери на трение по формуле Дарси-Вейсбаха если Re <2320, то , 2320 < Re < , то < Re < , то < Re , то 5) местные сопротивления по формуле Дарси

РАСЧЕТ КОРОТКИХ ТРУБОПРОВОДОВ В коротких трубопроводах местные потери соизмеримы с потерями по длине, и в расчете необходимо учитывать оба вида потерь напора.

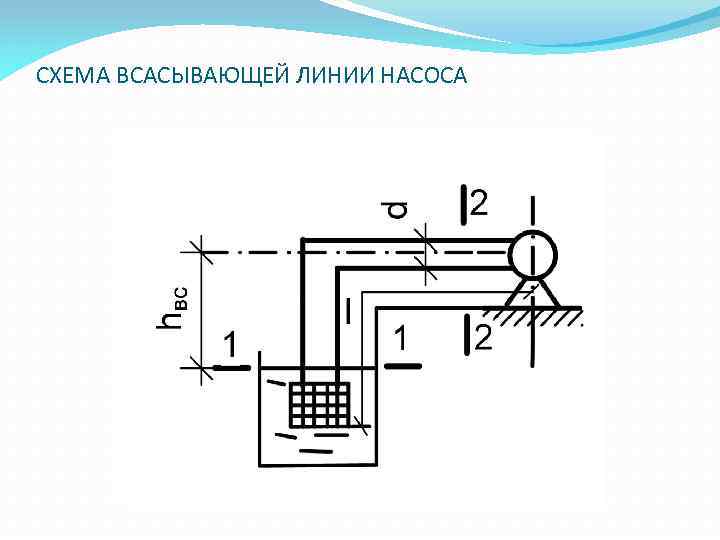
СХЕМА ВСАСЫВАЮЩЕЙ ЛИНИИ НАСОСА

РАСЧЕТ ВСАСЫВАЮЩЕЙ ЛИНИИ НАСОСА Принимаем расчетные сечения на поверхности воды в резервуаре 1 -1, перед входом в насос 2 -2. На поверхности воды в резервуаре давление равно атмосферному p 1=pа, z 1=0 и υ1=0, z 2=hвс Вакуумметрическая высота Высота всасывания насоса

РАСЧЕТ ДЛИННЫХ ТРУБОПРОВОДОВ Отличием длинных трубопроводов от коротких является незначительность потерь напора на местное сопротивление по сравнению с потерями по длине Местные сопротивления учитываются введением коэффициента, потери на местные сопротивления hм=(5 -10)% hl. Значением скоростного напора ввиду его малости по сравнению с пьезометрическими напорами, также можно пренебречь.

РАСЧЕТ ДЛИННЫХ ТРУБОПРОВОДОВ При решении практических задач обычно заданной или искомой величиной является расход воды, при этом – удельное сопротивление трубы, которое зависит от диаметра и коэффициента гидравлического трения λ

ГИДРАВЛИЧЕСКИЙ РАСЧЕТ СЛОЖНЫХ ТРУБОПРОВОДОВ К сложным трубопроводам относятся трубопроводы с переменным диаметром или расходом. Сложные трубопроводы: последовательно соединенные; параллельно соединенные; разветвленные.

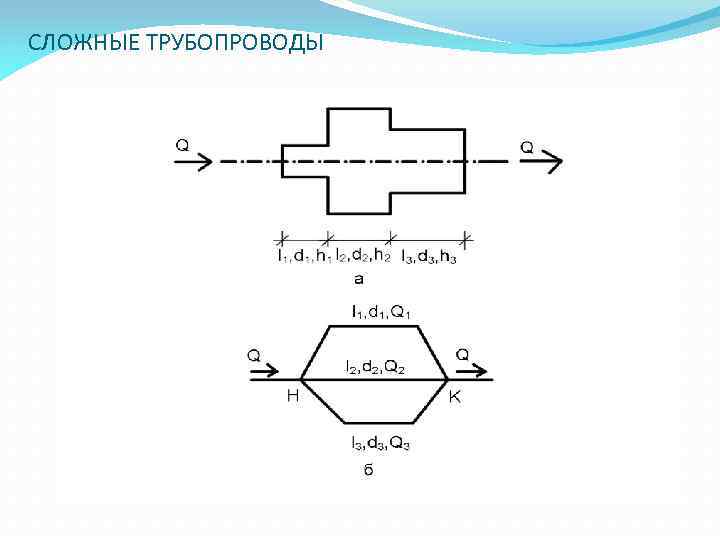
СЛОЖНЫЕ ТРУБОПРОВОДЫ

ПОСЛЕДОВАТЕЛЬНО СОЕДИНЕННЫЙ ТРУБОПРОВОД Последовательно соединенным называется трубопровод, состоящий из труб разного диаметра соединенных в одну нитку hн-к=h 1 +h 2+h 3 Q = const Параллельно соединенный – трубопровод, имеющий две общие точки Q=Q 1+Q 2+ Q 3 hн-к=const

ГРАФОАНАЛИТИЧЕСКИЙ МЕТОД РАСЧЕТА Характеристикой трубопровода называется зависимость потерь напора от расхода. Потребным напором называется напор в начале сечения трубопровода, необходимый для перемещения жидкости от начального до конечного сечения – остаточный свободный напор – приведенный геометрический напор

ХАРАКТЕРИСТИКА ТРУБОПРОВОДА

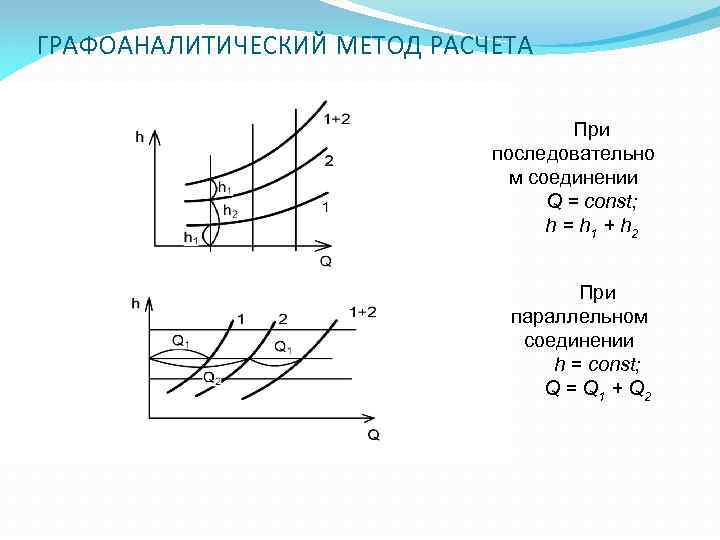
ГРАФОАНАЛИТИЧЕСКИЙ МЕТОД РАСЧЕТА При последовательно м соединении Q = const; h = h 1 + h 2 При параллельном соединении h = const; Q = Q 1 + Q 2

Тест 1 Если длина трубопровода 200 м, расход 0, 1 м 3/с, диаметр 0, 25, коэффициент гидравлического трения 0, 06, потери по длине 1 10, 18 2 0, 61 3 1, 02, 4 5, 09 2 Что является основной причиной потери напора в местных гидравлических сопротивлениях 1 наличие вихреобразований в местах изменения конфигурации потока; 2 трение жидкости о внутренние острые кромки трубопровода; 3 изменение направления и скорости движения жидкости; 4 шероховатость стенок трубопровода и вязкость жидкости 3 При подаче жидкости по параллельно соединенным трубопроводам 1, 2 и 3 общая потеря напора в них 1 Σh 1 = Σh 2 = Σh 3; 2 Σh 1 > Σh 2 > Σh 3; 3 Σh = Σh 1 – Σh 2 – Σh 3; 4 Σh = Σh 1 + Σh 2 + Σh 3 4 Что такое характеристика трубопровода? 1 зависимость давления на конце трубопровода от расхода жидкости; 2 зависимость потерь напора от давления; 3 зависимость потерь напора от расхода; 4 зависимость сопротивления трубопровода от его длины