ДВИЖЕНИЕ В ПРОСТРАНСТВЕ Мильц Христина и Иванова Ольга

ДВИЖЕНИЕ В ПРОСТРАНСТВЕ Мильц Христина и Иванова Ольга 11 а класс

ДВИЖЕНИЕ Движением в пространстве называется преобразование, при котором сохраняется расстояния между точками. Движение в пространстве обладает теми же свойствами, что и в плоскости и еще одним новым: движение переводит плоскости в плоскости.

ВИДЫ ДВИЖЕНИЯ 1. Симметрия: ─ осевая, ─ центральная, ─ скользящая. ─ зеркальная. 2. Параллельный перенос: 3. Поворот.

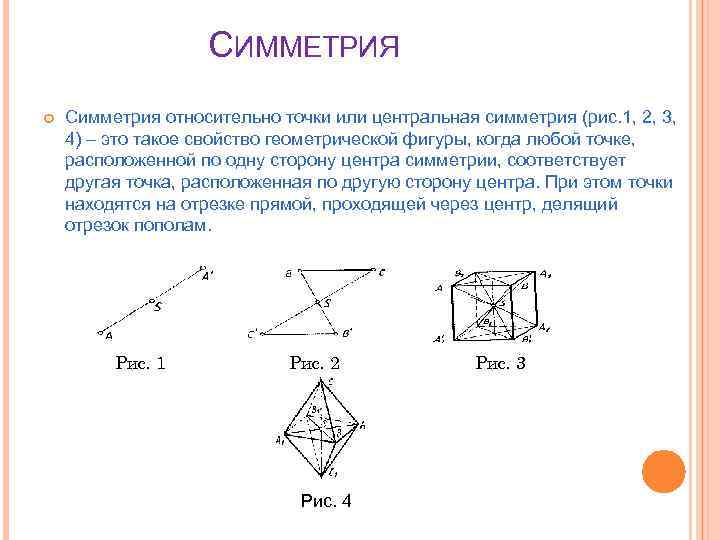СИММЕТРИЯ Симметрия относительно точки или центральная симметрия (рис. 1, 2, 3, 4) – это такое свойство геометрической фигуры, когда любой точке, расположенной по одну сторону центра симметрии, соответствует другая точка, расположенная по другую сторону центра. При этом точки находятся на отрезке прямой, проходящей через центр, делящий отрезок пополам. Рис. 1 Рис. 2 Рис. 4 Рис. 3

ОСЕВАЯ СИММЕТРИЯ Осевой симметрией с осью а называется такое отображение пространства на себя, при котором любая точка М переходит в симметричную ей точку М 1 относительно оси а.

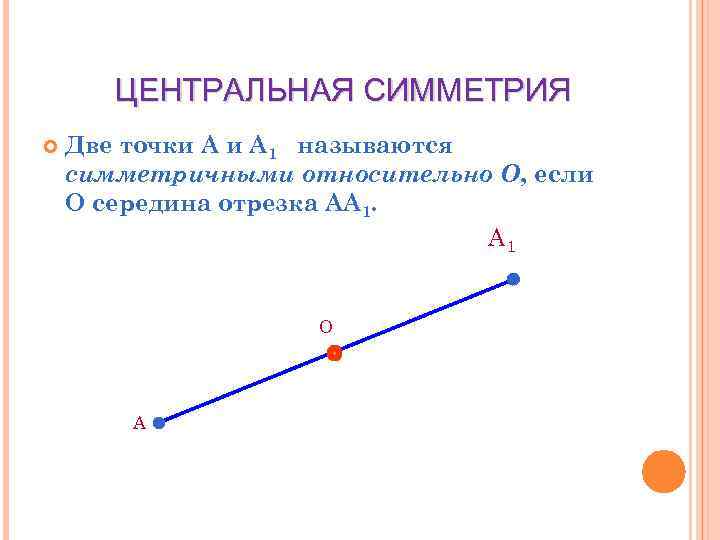ЦЕНТРАЛЬНАЯ СИММЕТРИЯ Две точки А 1 называются симметричными относительно О, если О середина отрезка АА 1. А 1 О А

ФИГУРЫ, ОБЛАДАЮЩИЕ ЦЕНТРАЛЬНОЙ СИММЕТРИЕЙ Примерами фигур, обладающих центральной симметрией, являются окружность и параллелограмм.

ЗЕРКАЛЬНАЯ СИММЕТРИЯ Если преобразование симметрии относительно плоскости переводит фигуру (тело) в себя, то фигура называется симметричной относительно плоскости, а данная плоскость – плоскостью плоскости симметрии этой фигуры.

ПАРАЛЛЕЛЬНЫЙ ПЕРЕНОС Параллельный перенос ― это частный случай движения, при котором все точки пространства перемещаются в одном и том же направлении на одно и то же расстояние.

СИММЕТРИЯ ПРЕДМЕТОВ НА ПЛОСКОСТИ Изображения предметов на плоскости из окружающего мира имеет ось или центр симметрии. С симметрией мы встречаемся в природе, быту, архитектуре и технике.

ФИГУРЫ, НЕ ИМЕЮЩИЕ ОСЕЙ СИММЕТРИИ К таким фигурам относятся параллелограмм, отличный от прямоугольника, разносторонний треугольник.

ПАРАЛЛЕЛЬНЫЙ ПЕРЕНОС В ПРОСТРАНСТВЕ Преобразование, при котором произвольная точка (х; у; z) фигуры переходит в точку (х+а; у+в; z+с), где числа а, в, с одни и те же для всех точек (х; у; z) , называется параллельным переносом Задается формулами: х’= х+а у’= у+в z’ = z+c

СВОЙСТВА ПАРАЛЛЕЛЬНОГО ПЕРЕНОСА Параллельный перенос есть движение При параллельном переносе точки смещаются по параллельным (или совпадающим) прямым на одно и то же расстояние. При параллельном переносе каждая прямая переходит в параллельную ей прямую (или в себя). Каковы бы ни были точки А и А’, существует единственный параллельный перенос, при котором точка А переходит в точку А’. При параллельном переносе в пространстве каждая плоскость переходит либо в себя, либо в параллельную ей плоскость.

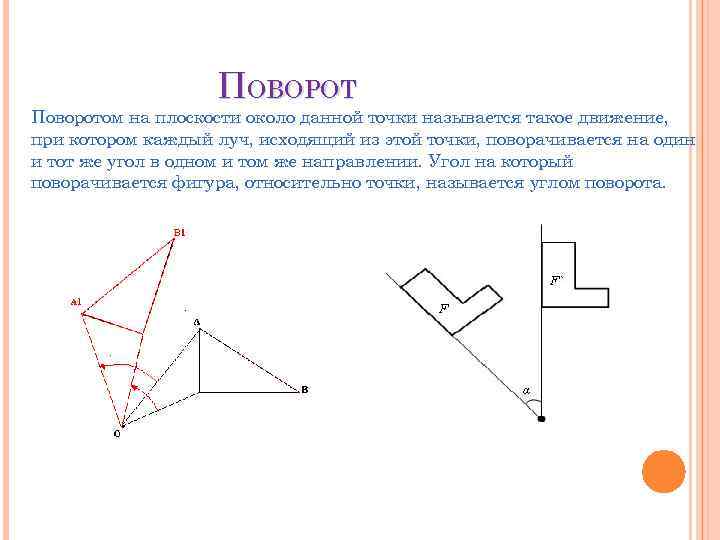ПОВОРОТ Поворотом на плоскости около данной точки называется такое движение, при котором каждый луч, исходящий из этой точки, поворачивается на один и тот же угол в одном и том же направлении. Угол на который поворачивается фигура, относительно точки, называется углом поворота.