Due Monday, 10/2 Problem Set 1 Demand Some Basics
Demand for Health Care • General models suffice … BUT • We want to look at the role of time and the role of insurance. • WHY? • Because often out-of-pocket costs are the smallest parts of the price of health care. • Only about 12% of health expenditures are out of pocket.
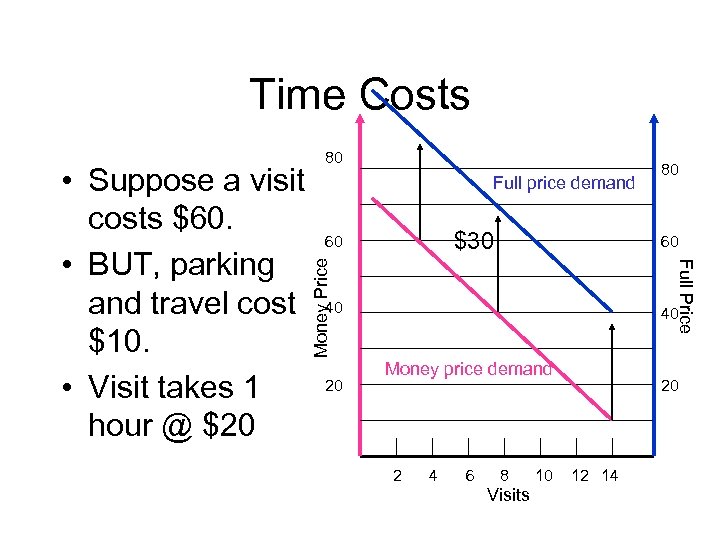
Time Costs Full price demand $30 60 Money Price 60 40 20 80 Full Price • Suppose a visit costs $60. • BUT, parking and travel cost $10. • Visit takes 1 hour @ $20 80 40 Money price demand 2 4 6 8 Visits 10 20 12 14
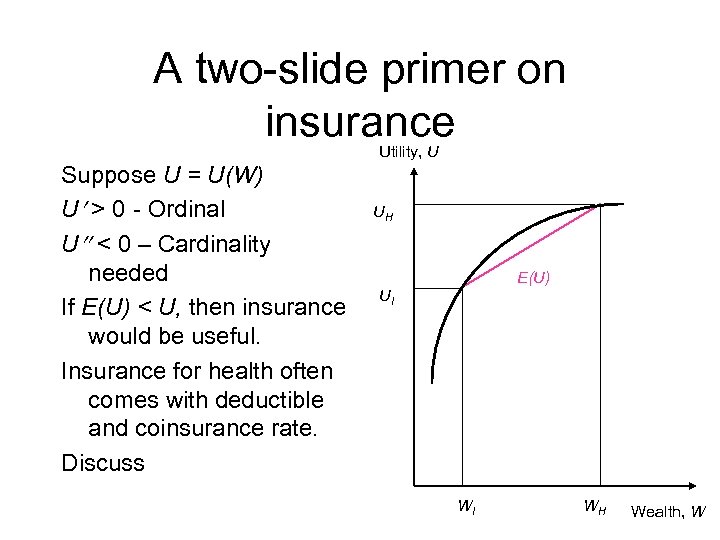
A two-slide primer on insurance Utility, U Suppose U = U(W) U > 0 - Ordinal U < 0 – Cardinality needed If E(U) < U, then insurance would be useful. Insurance for health often comes with deductible and coinsurance rate. Discuss UH E(U) UI WI WH Wealth, W
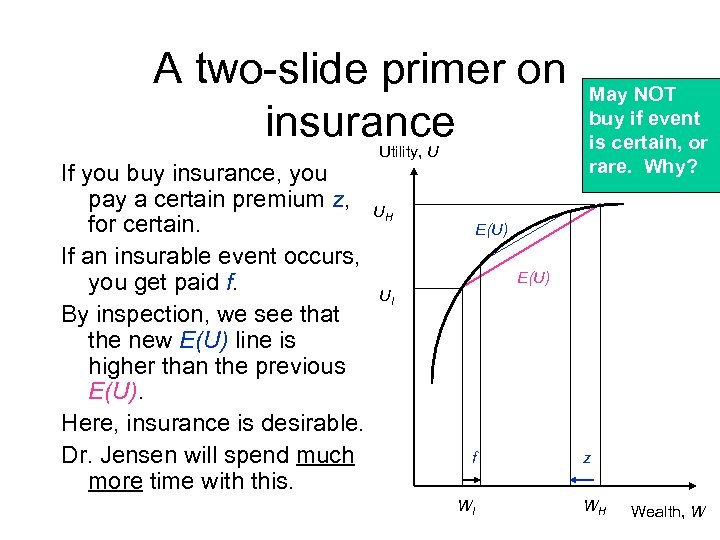
A two-slide primer on insurance If you buy insurance, you pay a certain premium z, for certain. If an insurable event occurs, you get paid f. By inspection, we see that the new E(U) line is higher than the previous E(U). Here, insurance is desirable. Dr. Jensen will spend much more time with this. Utility, U UH May NOT buy if event is certain, or rare. Why? E(U) UI f WI z WH Wealth, W
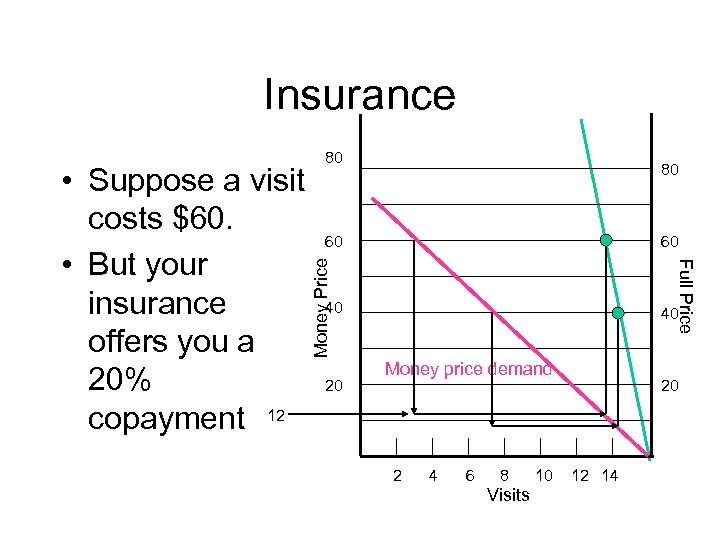
Insurance 80 60 Money Price 60 Full Price • Suppose a visit costs $60. • But your insurance offers you a 20% copayment 12 80 40 20 40 Money price demand 2 4 6 8 Visits 10 20 12 14
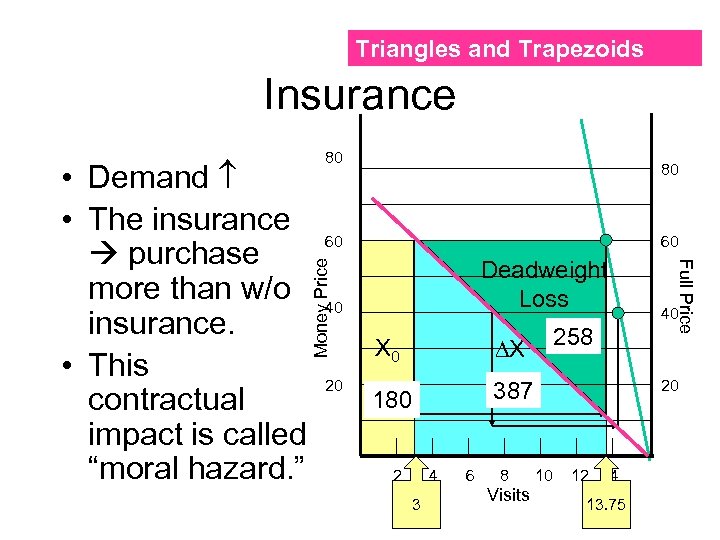
Triangles and Trapezoids Insurance 80 Money Price 60 60 Deadweight Loss 40 20 X 0 180 258 X 387 2 4 3 6 8 Visits Full Price • Demand • The insurance purchase more than w/o insurance. • This contractual impact is called “moral hazard. ” 80 40 20 10 12 14 13. 75
Put Together – A Simple Model Goods Where: M = Medical care w/ price pm z = all else w/ price 1 r = insurer’s share of payment; consumer’s coinsurance rate is 1 – r. y = income
A Simple Model (2) Time Where: T = Total time t = time cost per unit of medical care Tw = Time spent working Income Where: w = wage rate V = dividend income
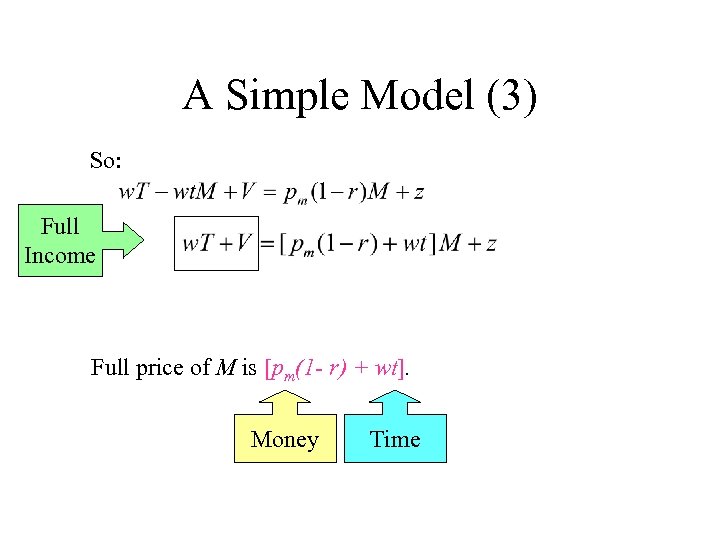
A Simple Model (3) So: Full Income Full price of M is [pm(1 - r) + wt]. Money Time
A Simple Model (4) Maximizing Utility Ultimate Constraint In problem sets, USE this condition to solve!
Another perspective First Order Conditions Implies that time cost of z = 0 If we ignore time costs, RHS will be too small. We’ll buy too much M.
Impact of a pure income increase V? watch carefully Some Comparative Statics 0 Cramer’s Rule Put in 1 everywhere you see d. V, 0 elsewhere. 0 -1 0 1 Remember: = Uz. Positive!!!
Some Comparative Statics Impact of an increase in pm? (1 -r) 0 M(1 -r) 1 1 Remember: = Uz.
r=insurer’s share What do we get?
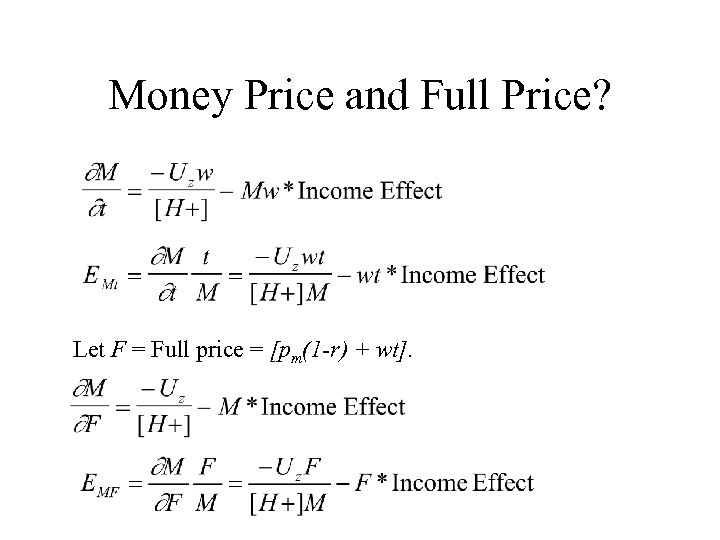
Money Price and Full Price? Let F = Full price = [pm(1 -r) + wt].
![If you look at things closely: Where, F = [pm(1 -r) + wt]. Compare](https://present5.com/presentation/5006c4795da62e724fadb160d69dbefd/image-17.jpg "If you look at things closely: Where, F = [pm(1 -r) + wt]. Compare")
If you look at things closely: Where, F = [pm(1 -r) + wt]. Compare elasticities.
Change in w?
What do we get? Price Effect! Negative Income Effect! Positive
What do we do with this? • Look at share of health care for individual or national budget. s = pq/y. This is an identity, but if we get behavioral, we have: s = p q (p, y) /y. ds/dp = (p/y)( q/ p) + q/y. = (p/y) ( q/ p)(p/q)(q/p) + q/y = (Ep + 1) (q/y). What does this mean? We can show that: (ds/dp)(p/s) = (Ep + 1). Figure it out.
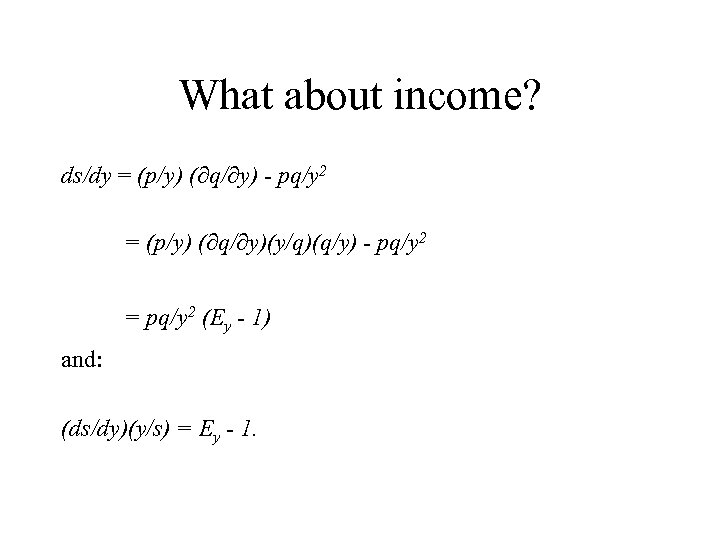
What about income? ds/dy = (p/y) ( q/ y) - pq/y 2 = (p/y) ( q/ y)(y/q)(q/y) - pq/y 2 = pq/y 2 (Ey - 1) and: (ds/dy)(y/s) = Ey - 1.
Measuring Demand • • Individual Services Firm services (germane to anti-trust) Market demand -- very difficult to handle. Students will collect some data and say, “I’m estimating a demand (or a supply) regression. ”
Identification price Demand: Qd = a - b. P + c. N + d. Y, where N = population, Y = income. Supply: Qs = e + f. P First question: Both are related to P. How do you know which one you are estimating? Solve as P =[(a-e)/(b+f) + c. N/(b+f) + d. Y/(b+f)] S D quantity
![P =[(a-e)/(b+f) + c. N/(b+f) + d. Y/(b+f)] Identification D price When we substitute](https://present5.com/presentation/5006c4795da62e724fadb160d69dbefd/image-24.jpg "P =[(a-e)/(b+f) + c. N/(b+f) + d. Y/(b+f)] Identification D price When we substitute")
P =[(a-e)/(b+f) + c. N/(b+f) + d. Y/(b+f)] Identification D price When we substitute into either: Qd = a - b. P + c. N + d. Y or: Qs = e + f. P, You get: It’s easy to see S that they’re not the same! Or: quantity
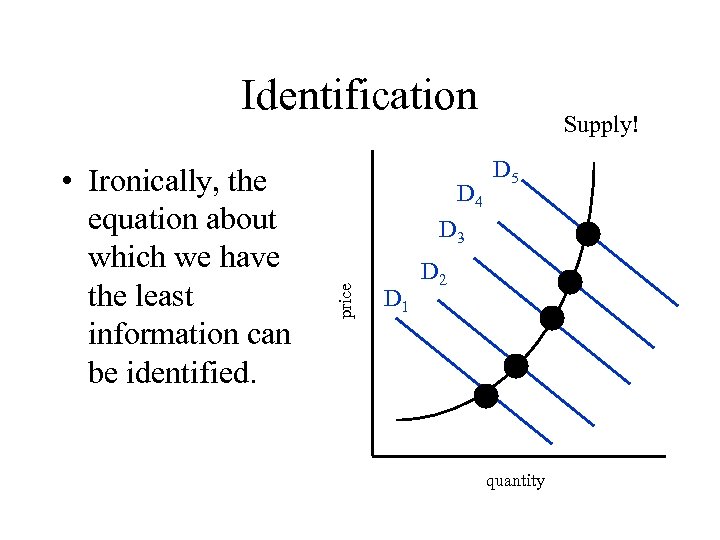
Identification D 4 D 5 D 3 price • Ironically, the equation about which we have the least information can be identified. Supply! D 1 D 2 quantity
Скачать презентацию Due Monday 10 2 Problem Set 1 Demand Some
5006c4795da62e724fadb160d69dbefd.ppt