Dual lookups in Pattern Databases Ariel Felner Ben-Gurion

Dual lookups in Pattern Databases Ariel Felner, Ben-Gurion Univ. Israel Uzi Zahavi, Bar-Ilan Univ. Israel Jonathan Schaeffer, Univ. of Alberta, Canada Robert C. Holte, Univ. of Alberta, Canada 1

Overview • • • Heuristic search and A* Test domains Pattern databases Dual lookups in pattern databases Experimental results 2

A* • Best-first search with a cost function of f(n)=g(n)+h(n) • g(n): actual distance from the initial state to n • h(n): estimated remained distance from n to the goal state. • h(n) is admissible if it is always underestimating • Examples of h: Air distance, Manhattan Distance 3

Attributes of A* • If h(n) is admissible then A* is guaranteed to return an optimal (shortest) solution • A* is admissible, complete and optimally effective. [Pearl & Dechter 84] • IDA* is a linear space version of A* [Korf 85] which uses DFS iterations. 4

Domains • • • 15 puzzle 10^13 states First solved by [Korf 85] with IDA* and Manhattan distance Takes 53 seconds 24 puzzle 10^24 states First solved by [Korf 96] Takes 2 days 5

Domains • • Rubik’s cube 10^19 states First solved by [Korf 97] Takes 2 days to solve 6

(n, k) Top Spin Puzzle • n tokens arranged in a ring • States: any possible permutation of the tokens • Operators: Any k consecutive tokens can be reversed • The (17, 4) version has 10^13 states • The (20, 4) version has 10^18 states 7

How to improve search? • • • Enhanced algorithms: Perimeter-search [Delinberg and Nilson 95] RBFS [Korf 93] Frontier-search [Korf and Zang 2003] Breadth-first heuristic search [Zhou and Hansen 04] They all try to better explore the search tree. • Better heuristics: more parts of the search tree will be pruned. 8

Subproblems-Abstractions • Many problems can be abstracted into subproblems that must be also solved. • A solution to the subproblem is a lower bound on the entire problem. • Example: Rubik’s cube [Korf 97] • Problem: 3 x 3 x 3 Rubik’s cube Subproblem: 2 x 2 x 2 Corner cubies. 9

Pattern Databases heuristics • A pattern database [Culbreson & Schaeffer 96] is a lookup table that stores solutions to all configurations of the subproblem / abstraction / pattern. • This table is used as a heuristic during the search. • Example: Rubik’s cube. • Has 10^19 States. • The corner cubies subproblem has 88 Million states • A table with 88 Million entries fits in memory [Korf 97]. Search space Mapping/Projection Pattern space 10

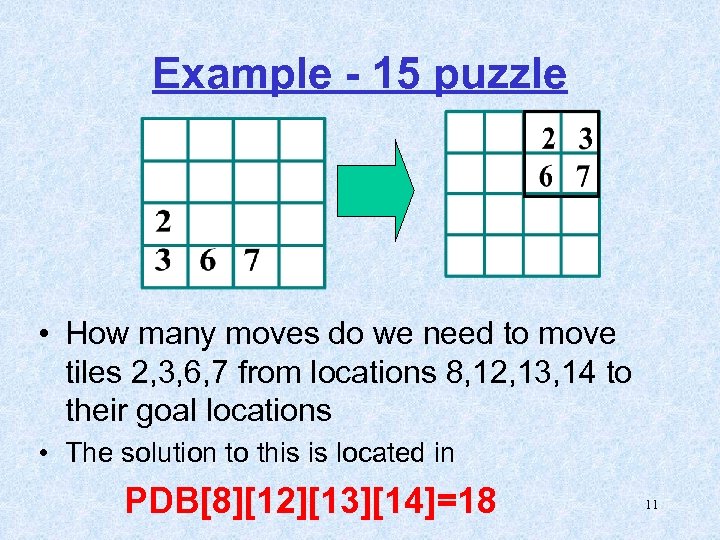
Example - 15 puzzle • How many moves do we need to move tiles 2, 3, 6, 7 from locations 8, 12, 13, 14 to their goal locations • The solution to this is located in PDB[8][12][13][14]=18 11

Disjoint Additive PDBs (DADB) • If you have many PDBS, take their maximum 7 -8 • Values of disjoint databases can be added and are still admissible [Korf & Felner: AIJ-02, Felner, Korf & Hanan: JAIR-04] 12

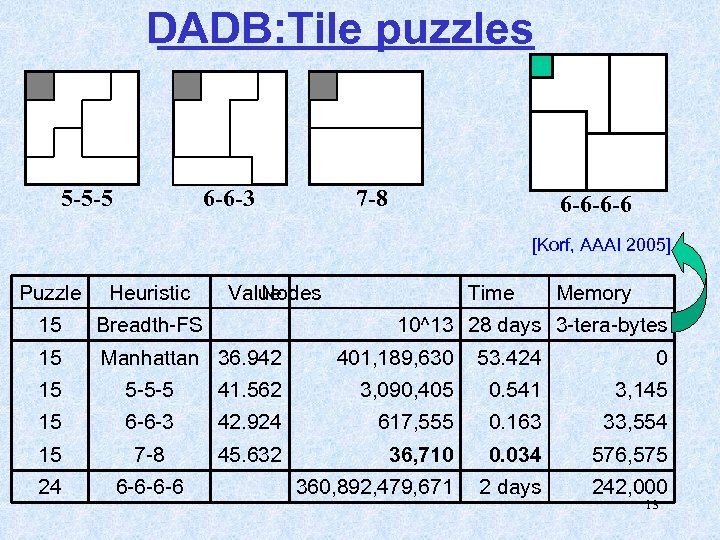
DADB: Tile puzzles 5 -5 -5 6 -6 -3 7 -8 6 -6 -6 -6 [Korf, AAAI 2005] Puzzle Heuristic Value Nodes 15 Breadth-FS 15 Manhattan 36. 942 Time Memory 10^13 28 days 3 -tera-bytes 401, 189, 630 53. 424 0 15 5 -5 -5 41. 562 3, 090, 405 0. 541 3, 145 15 6 -6 -3 42. 924 617, 555 0. 163 33, 554 15 7 -8 45. 632 36, 710 0. 034 576, 575 24 6 -6 -6 -6 360, 892, 479, 671 2 days 242, 000 13

Symmetries in PDBs • Symmetric lookups were already performed by the first PDB paper of [Culberson & Schaeffer 96] • examples – Tile puzzles: reflect the tiles about the main diagonal. – Rubik’s cube: rotate the cube • We can take the maximum among the different lookups • These are all geometrical symmetries • We suggest a new type of symmetry!! 7 8 14

Regular and dual representation • Regular representation of a problem: • Variables – objects (tiles, cubies etc, ) • Values – locations • Dual representation: • Variables – locations • Values – objects 15

Regular vs. Dual lookups in PDBs • Regular question: Where are tiles {2, 3, 6, 7} and how many moves are needed to gather them to their goal locations? • Dual question: Who are the tiles in locations {2, 3, 6, 7} and how many moves are needed to distribute them to their goal locations? 16

Regular and dual lookups • Regular lookup: PDB[8, 12, 13, 14] • Dual lookup: PDB[9, 5, 12, 15] 17

Regular and dual in Top. Spin • Regular lookup for C : PDB[1, 2, 3, 7, 6] • Dual lookup for C: PDB[1, 2, 3, 8, 9] 18

Dual lookups • Dual lookups are possible when there is a symmetry between locations and objects: – Each object is in only one location and each location occupies only one object. • Good examples: Top. Spin, Rubik’s cube • Bad example: Towers of Hanoi • Problematic example: Tile Puzzles 19

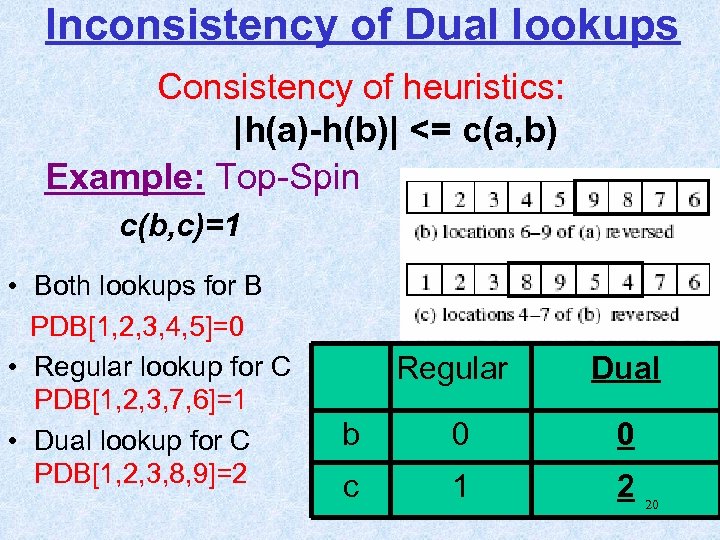
Inconsistency of Dual lookups Consistency of heuristics: |h(a)-h(b)| <= c(a, b) Example: Top-Spin c(b, c)=1 • Both lookups for B PDB[1, 2, 3, 4, 5]=0 • Regular lookup for C PDB[1, 2, 3, 7, 6]=1 • Dual lookup for C PDB[1, 2, 3, 8, 9]=2 Regular Dual b 0 0 c 1 2 20

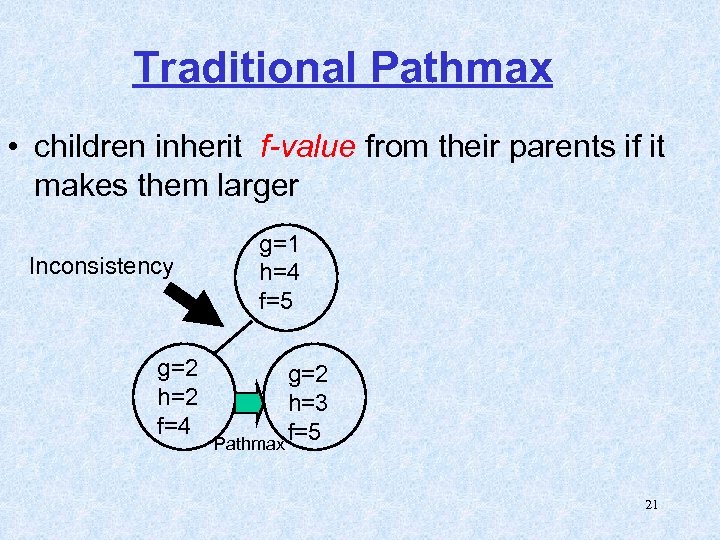
Traditional Pathmax • children inherit f-value from their parents if it makes them larger Inconsistency g=2 h=2 f=4 g=1 h=4 f=5 g=2 h=3 f=5 Pathmax 21

Bidirectional pathmax (BPMX) h-values 2 5 h-values 4 BPMX 1 5 3 • Bidirectional pathmax: h-values are propagated in both directions decreasing by 1 in each edge. – If the IDA* threshold is 2 then with BPMX the right child will not even be generated!! 22

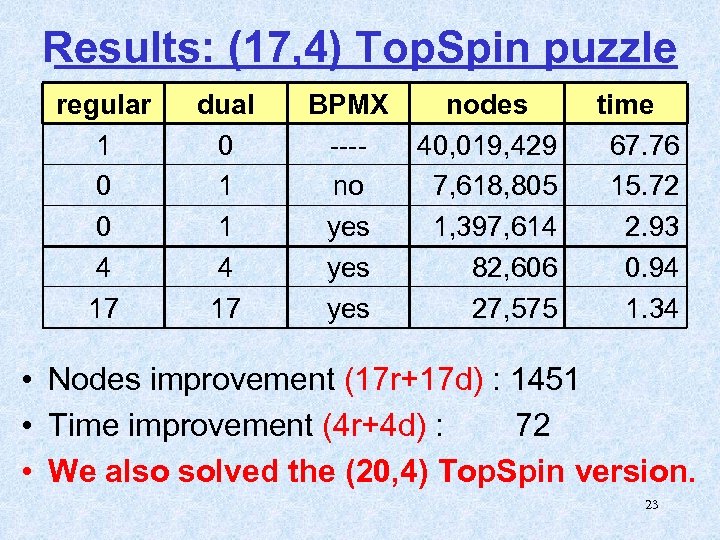
Results: (17, 4) Top. Spin puzzle regular 1 0 0 4 17 dual 0 1 1 4 17 BPMX ---no yes yes nodes 40, 019, 429 7, 618, 805 1, 397, 614 82, 606 27, 575 time 67. 76 15. 72 2. 93 0. 94 1. 34 • Nodes improvement (17 r+17 d) : 1451 • Time improvement (4 r+4 d) : 72 • We also solved the (20, 4) Top. Spin version. 23

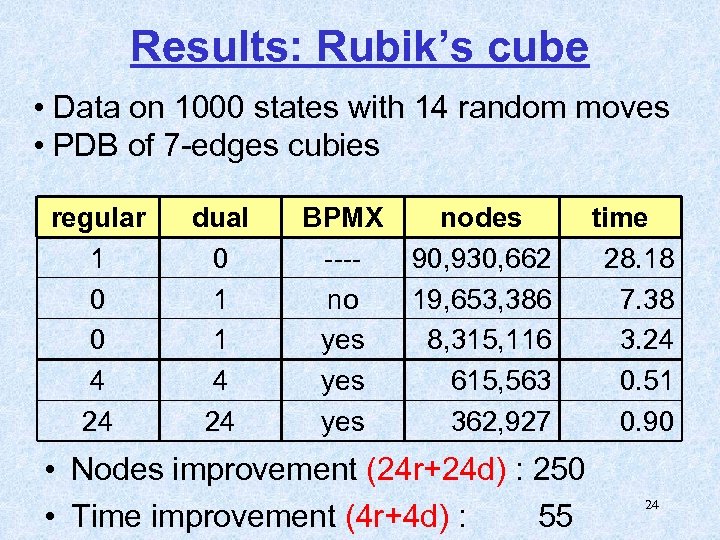
Results: Rubik’s cube • Data on 1000 states with 14 random moves • PDB of 7 -edges cubies regular 1 0 0 4 24 dual 0 1 1 4 24 BPMX ---no yes yes nodes 90, 930, 662 19, 653, 386 8, 315, 116 615, 563 362, 927 • Nodes improvement (24 r+24 d) : 250 • Time improvement (4 r+4 d) : 55 time 28. 18 7. 38 3. 24 0. 51 0. 90 24

Results: Rubik’s cube • With duals we improved Korf’s results on random instances by a factor of 1. 5 using exactly the same PDBs. 25

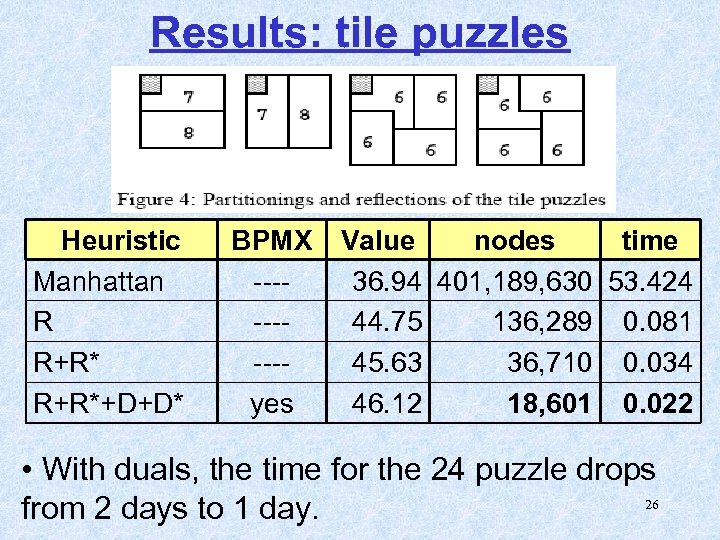
Results: tile puzzles Heuristic Manhattan R R+R*+D+D* BPMX -----yes Value nodes time 36. 94 401, 189, 630 53. 424 44. 75 136, 289 0. 081 45. 63 36, 710 0. 034 46. 12 18, 601 0. 022 • With duals, the time for the 24 puzzle drops 26 from 2 days to 1 day.

Discussion • Results for the Top. Spin and Rubik’s cube are better than those of the tile puzzles • Dual PDB lookups and BPMX cutoffs are more effective if each operators changes larger part of the states. • This is because the identity of the objects being queried in consecutive states are dramatically changed 27

Summary • Dual PDB lookups • BPMX cutoffs for inconsistent heuristics • State of the art solvers. 28

Future work • • Duality in search spaces Which and how many symmetries to use Other sources of inconsistencies Better ways for propagating inconsistencies 29