3da0f27c6c7f124a376fa22d9e20288f.ppt
- Количество слайдов: 23

Dual Analysis for Proving Safety and Finding Bugs Corneliu Popeea Technische Universität München Wei-Ngan Chin National University of Singapore Symposium on Applied Computing – SAC 2010, Sierre, Switzerland

Why do Program Analysis? Programs have bugs Program analysis for • proving safety • finding bugs 2

Automated Approaches • Program testing: – detects presence of bugs – examines some paths, not all (under-approximation of the program semantics) – compromises on program safety • Verification: – examines all paths (over-approximation of the program semantics) – may report false bugs 3

Combination of Testing and Verification • Search for both bugs and safety proofs • Combination of under- and over-approximation • Projects at Microsoft Research – Synergy, Smash: analysis of Windows device drivers 4

Our Methodology • Extend a static analyzer aimed at proving safety to discover (true) bugs – based only on over-approximation analysis – dual simultaneous analyses 5
![Quicksort Example void quicksort (float a[], int l, int h) { if (l < Quicksort Example void quicksort (float a[], int l, int h) { if (l <](https://present5.com/presentation/3da0f27c6c7f124a376fa22d9e20288f/image-6.jpg)
Quicksort Example void quicksort (float a[], int l, int h) { if (l < h) { int p = partition (a, l, h); quicksort (a, l, p-1); quicksort (a, p+1, h); }} int partition (…) { … v = a[l]; … a[m] = v; …} WANTED 2 conditions on inputs a, I, h Never. Bug - guarantees safety of bound checks Must. Bug - guarantees execution triggers a bug 6

Concrete Semantics and Abstraction • Three possible outcomes for a program execution: ok - for a safe/successful execution err - for an unsafe execution (due to a failed assertion) loop - for a non-terminating execution • Compute over-approximations for inputs leading to: OK - all possibly safe executions ERR - all possibly unsafe executions OK ERR • Example: OK=true, ERR=true 7

Forward Reasoning Rules • Formulated using Hoare-style triples: • Rule for function call: • Summaries of recursive functions: – computed by abstract interpretation 8

Partial Correctness and Bug Finding • NEVER_BUG = OK Æ : ERR Partial correctness Any input satisfying this condition is guaranteed to lead to ok or loop. Bug finding • MUST_BUG = ERR Æ : OK Any input satisfying this condition is guaranteed to lead to err or loop. • MAY_BUG = OK Æ ERR Any input satisfying this condition may lead to either ok , err or loop. OK ERR NEVER BUG MAY BUG MUST BUG 9
![Quicksort Example void quicksort (float a[], int l, int h) { … } Compute Quicksort Example void quicksort (float a[], int l, int h) { … } Compute](https://present5.com/presentation/3da0f27c6c7f124a376fa22d9e20288f/image-10.jpg)
Quicksort Example void quicksort (float a[], int l, int h) { … } Compute OK and ERR using a disjunctive abstract domain: Characterization of quicksort inputs: NEVER_BUG = OK MUST_BUG = ERR 10

Detect Non-termination • Some inputs may be outside both OK and ERR. LOOP = : OK Æ : ERR Any input satisfying this condition is guaranteed to lead to loop. • Example: void ex_fig 9() { int x, y; x: =0; y: =0; l 5: while (y>=0) {y: =y+x; } l 6: assert(false); } OK LOOP ERR • Loop summary: {OK: (x<0 Ç y<0), ERR: false, }LOOP: (x¸ 0 Æ y¸ 0)} • Function summary: {OK: false, ERR. l 5. LOOP: true, ERR. l 6: false} 11

Dualyzer: Prototype Implementation • Written in the Haskell language: – uses a Presburger arithmetic solver: Omega library – disjunctive fixed-point analyzer • Objectives: – prove program safety + confirm true bugs • Test programs: – small programs: binary search, queens, quick sort – numerical benchmarks: Fast Fourier Transform, LU decomposition, Linpack 12
![Dualyzer and Blast [Henzinger-Jhala-et-al POPL 02] • Correct programs: can prove safety of bound Dualyzer and Blast [Henzinger-Jhala-et-al POPL 02] • Correct programs: can prove safety of bound](https://present5.com/presentation/3da0f27c6c7f124a376fa22d9e20288f/image-13.jpg)
Dualyzer and Blast [Henzinger-Jhala-et-al POPL 02] • Correct programs: can prove safety of bound checks? Correct Programs bsearch bsort initarr queens quick-sort sentinel FFT LU SOR Linpack Blast Proved? (secs) * 0. 1 √ 1. 1 √ 3. 4 √ * * √ √ * 28 1. 3 0. 5 7. 2 2. 1 408 • Faulty programs: can identify true bugs? Dualyzer Proved? (secs) √ 3. 1 √ 0. 8 √ 0. 2 √ 1. 4 √ * √ √ 1. 5 0. 1 13. 5 14. 3 3. 5 38. 9 Faulty Programs Dualyzer May Must (secs) bsort 0 1 2. 44 initarr 0 1 1. 12 quick-sort 0 1 2. 24 sentinel 0 1 1. 31 13
![Verisec Benchmark [Ku-Hart-Chechik-Lie ASE 07] • Small challenging testcases: – actual vulnerabilities from CVE Verisec Benchmark [Ku-Hart-Chechik-Lie ASE 07] • Small challenging testcases: – actual vulnerabilities from CVE](https://present5.com/presentation/3da0f27c6c7f124a376fa22d9e20288f/image-14.jpg)
Verisec Benchmark [Ku-Hart-Chechik-Lie ASE 07] • Small challenging testcases: – actual vulnerabilities from CVE database – corrected versions of these testcases • Dualyzer found 2 unknown bugs in the corrected testcases: – off-by-one buffer error [Spam. Assassin testcase] – non-termination bug [Samba testcase] 14
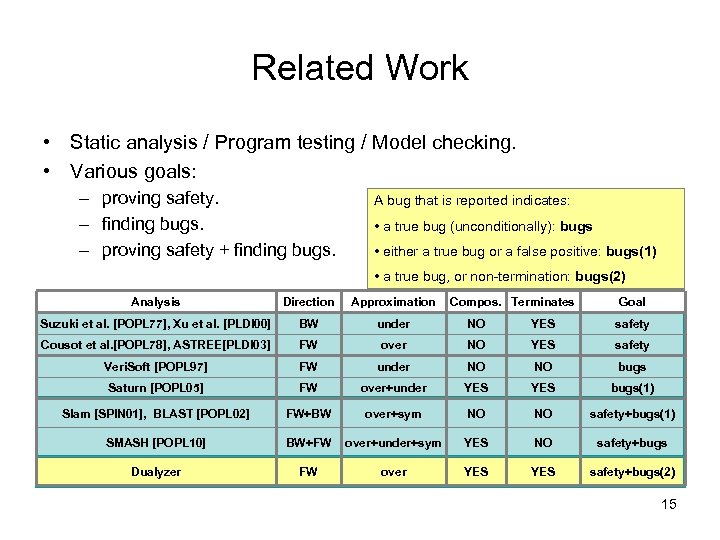
Related Work • Static analysis / Program testing / Model checking. • Various goals: – proving safety. – finding bugs. – proving safety + finding bugs. A bug that is reported indicates: • a true bug (unconditionally): bugs • either a true bug or a false positive: bugs(1) • a true bug, or non-termination: bugs(2) Analysis Direction Approximation Compos. Terminates Goal Suzuki et al. [POPL 77], Xu et al. [PLDI 00] BW under NO YES safety Cousot et al. [POPL 78], ASTREE[PLDI 03] FW over NO YES safety Veri. Soft [POPL 97] FW under NO NO bugs Saturn [POPL 05] FW over+under YES bugs(1) Slam [SPIN 01], BLAST [POPL 02] FW+BW over+sym NO NO safety+bugs(1) SMASH [POPL 10] BW+FW over+under+sym YES NO safety+bugs Dualyzer FW over YES safety+bugs(2) 15

Conclusion • Dual analyses based on over-approximation – prove program safety – find bugs • Find non-termination inputs • Prototype implementation 16

Thank you for attention! Questions?

Additional slides follow 18
![Example void g(int[] a, ref int x) { if (x<=0) then () else { Example void g(int[] a, ref int x) { if (x<=0) then () else {](https://present5.com/presentation/3da0f27c6c7f124a376fa22d9e20288f/image-19.jpg)
Example void g(int[] a, ref int x) { if (x<=0) then () else { a[x]: =0; //assert(0 <= x < a) x: =x-1; g(a, x) }} 19
![Constraint Abstractions - Dual Analysis void g(int[] a, ref int x) { if (x<=0) Constraint Abstractions - Dual Analysis void g(int[] a, ref int x) { if (x<=0)](https://present5.com/presentation/3da0f27c6c7f124a376fa22d9e20288f/image-20.jpg)
Constraint Abstractions - Dual Analysis void g(int[] a, ref int x) { if (x<=0) then () else { a[x]: =0; x: =x-1; g(a, x) }} For general recursion, the ERR cons-abs. may depend on OK. • Constraint abstractions: g. OK(a, x, x') = (x· 0 Æ x'=x) Ç (x>0 Æ 0·x<a Æ 9 x 1¢(x 1=x-1Æ g. OK(a, x 1, x'))) g. ERR(a, x) = x>0 Æ (x<0 Ç x¸a Ç 0·x<a Æ 9 x 1¢(x 1=x-1 Æ g. ERR(a, x 1))) • Results of fixpoint approximation: g. OK(a, x, x') = (x· 0Æx'=x) Ç (1·x < a Æx'=0) g. ERR(a, x) = (x>0 Æ x¸a) OK ERR • Function summary: {g. OK, g. ERR}. 20

Precise Error Tracing • Report the label of calls that lead to a bug void foo(int x, int y) { if x=y then { l 3: error } else () } {OK: x y, ERR. l 3: x=y} void goo(int x) { l 1: foo(x, x+1); l 2: foo(x, 3); } {OK: x 3, ERR. l 1. l 3: false, ERR. l 2. l 3: x=3} OK ERR. l 2. l 3 ERR. l 1. l 3 21
![Examples from SYNERGY [Gulavani-et-al FSE 06] Synergy: software model checker + testing – discovers Examples from SYNERGY [Gulavani-et-al FSE 06] Synergy: software model checker + testing – discovers](https://present5.com/presentation/3da0f27c6c7f124a376fa22d9e20288f/image-22.jpg)
Examples from SYNERGY [Gulavani-et-al FSE 06] Synergy: software model checker + testing – discovers a true BUG; – proves that the program is SAFE; – times-out during refinement loop (ABORT). Programs SYNERGY ex_fig 1 ex_fig 3 ex_fig 4 ex_fig 6 ex_fig 7 ex_fig 8 ex_fig 9 BUG SAFE ABORT Dualyzer May Must 0 1 0 0 0 1(LOOP) 22
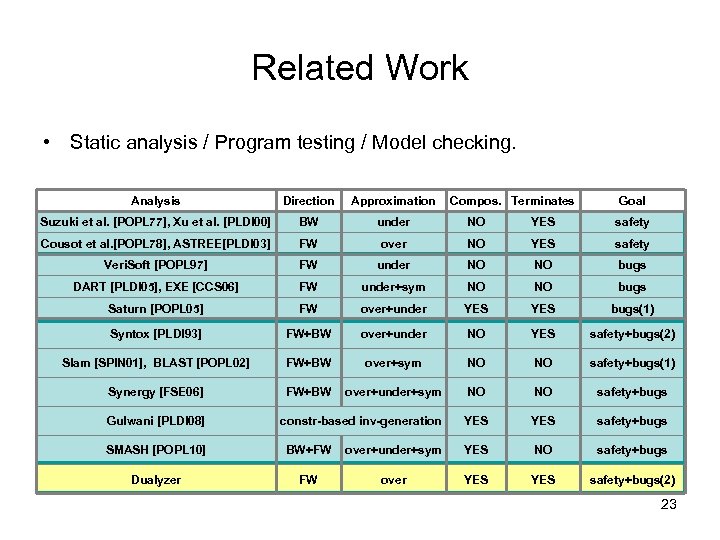
Related Work • Static analysis / Program testing / Model checking. Analysis Direction Approximation Suzuki et al. [POPL 77], Xu et al. [PLDI 00] BW under NO YES safety Cousot et al. [POPL 78], ASTREE[PLDI 03] FW over NO YES safety Veri. Soft [POPL 97] FW under NO NO bugs DART [PLDI 05], EXE [CCS 06] FW under+sym NO NO bugs Saturn [POPL 05] FW over+under YES bugs(1) Syntox [PLDI 93] FW+BW over+under NO YES safety+bugs(2) Slam [SPIN 01], BLAST [POPL 02] FW+BW over+sym NO NO safety+bugs(1) Synergy [FSE 06] FW+BW over+under+sym NO NO safety+bugs constr-based inv-generation YES safety+bugs Gulwani [PLDI 08] Compos. Terminates Goal SMASH [POPL 10] BW+FW over+under+sym YES NO safety+bugs Dualyzer FW over YES safety+bugs(2) 23
3da0f27c6c7f124a376fa22d9e20288f.ppt