DREAM IDEA PLAN IMPLEMENTATION 1 Linear-Control-Systems Present

DREAM IDEA PLAN IMPLEMENTATION 1

Linear-Control-Systems Present to: Amirkabir University of Technology (Tehran Polytechnic) & Semnan University Dr. Kourosh Kiani Email: kkiani 2004@yahoo. com Email: Kourosh. kiani@aut. ac. ir Web: aut. ac. com 2

Lecture 13 3

PID Control 4

PID Tuning n n Controller tuning---the process of selecting the controller parameters to meet given performance specifications PID tuning rules---selecting controller parameter values based on experimental step responses of the controlled plant The first PID tuning rules proposed by Ziegler and Nichols in 1942 Our exposition based on K. Ogata, Modern Control Engineering, Prentice Hall, Fourth Edition, 2002, Chapter 10 5

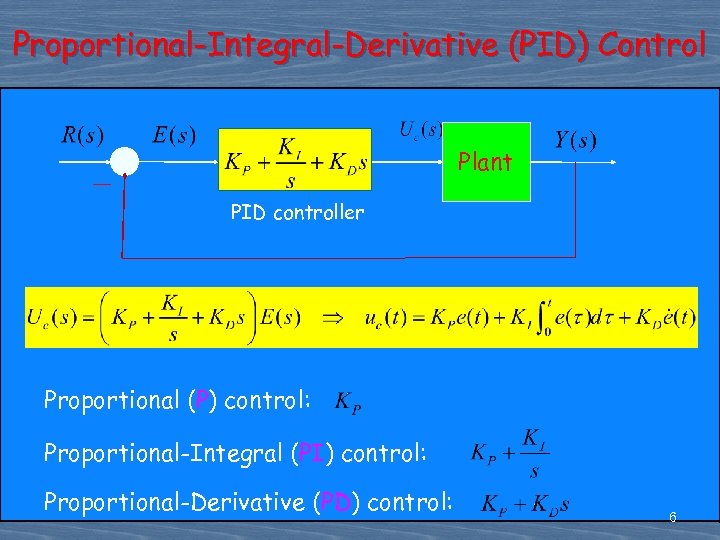Proportional-Integral-Derivative (PID) Control Plant PID controller Proportional (P) control: Proportional-Integral (PI) control: Proportional-Derivative (PD) control: 6

More than half of the industrial controllers in use today utilize PID or modified PID control schemes. When the mathematical model of the plant is unknown and therefore analytical design cannot be used, PID control proves to be most useful. Many different types of tuning rules have been developed to adjust the parameters of PID controllers on-site. 7

Ziegler-Nichols Rules for Tuning PID Controllers Ziegler and Nichols proposed rules for determining values of the proportional gain Kp, integral time Ti and derivative time Td based on the transient response of a given plant. There are two methods called Ziegler-Nichols tuning rules: the first method and the second method. 8

First method. --Obtain the response of the plant to a unit-step input --If the plant involves neither integrator nor dominant complex-conjugate poles, then it step response exhibits an S-shape curve , the first method can be applied. unit-step input Plant S-shape response The S-shape curve may be characterized by two constants: Delay time L and Time constant T 9

PID Tuning---First Method Start with obtaining the step response 10

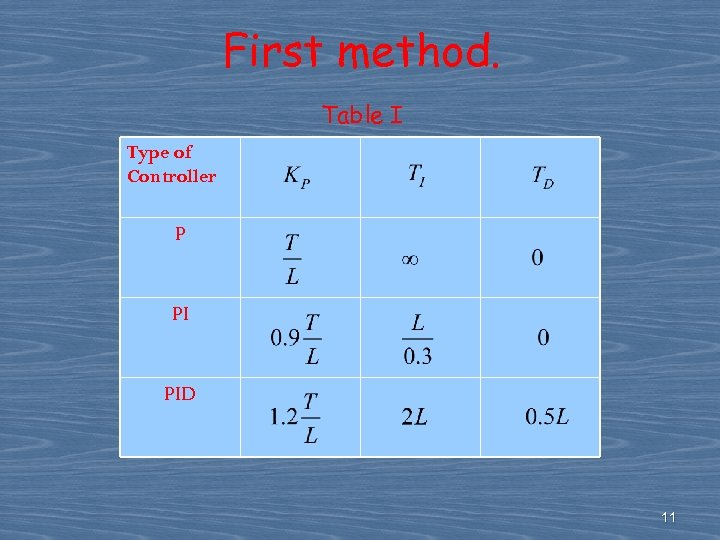First method. Table I Type of Controller P PI PID 11

Transfer Function of PID Controller Tuned Using the First Method 12

Second method. --Set and use the proportional control only --Increase from 0 to ∞ to a critical value at which the output first exhibits sustained oscillations --If the output does not exhibit sustained oscillations for whatever value may take, then this method does not apply. Plant 13

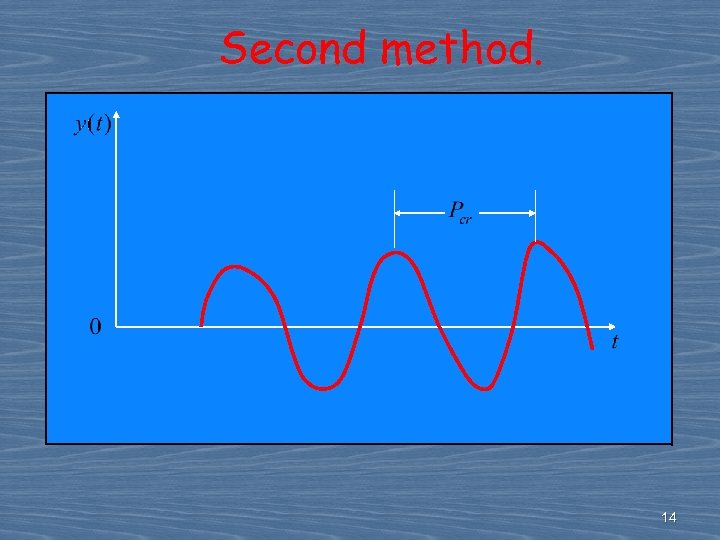Second method. 14

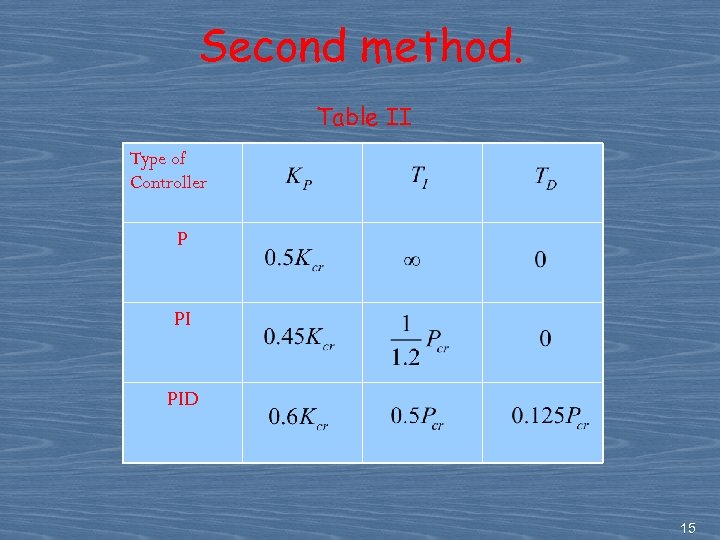Second method. Table II Type of Controller P PI PID 15

Transfer Function of PID Controller Tuned Using the Second Method 16

Comments Ziegler-Nichols tuning rules have been widely used to tune PID controllers in process control systems where the plant dynamics are not precisely known. If the plant dynamics are known, many analytical and graphical approaches to the design of PID controllers are available, in addition to Ziegler. Nichols tuning rules 17

Example Consider the following control system PID controller Plant Design a PID controller to make the maximum overshoot of the system to be approximately 25% or less. Solution. We start design the PID controller by applying Ziegler-Nichols rules. Here the transfer function of the plant is known, we can use analytical method instead of experimental method. 18

PID controller Plant The PID controller has the transfer function Since the plant has a integrator, we use the second method. By setting , we obtain the closed-loop TF: 19

PID controller Plant The value of Kp that makes the system marginally stable so that sustained oscillation occurs can be obtained by use of Routh’s stability criterion. The CE of the closed-loop system is The Routh’s array When Kp=30, the closed-loop system is marginally stable. Thus the critical gain 20

PID controller Plant With Kp set to Kcr(=30), the CE becomes To find the frequency of the sustained oscillation, we substitute s=jw into the CE as follows: or Hence the period of the sustained oscillation is 21

PID controller Plant With Table II, we determine the parameters of the PID controller as follows: The transfer function of the PID controller is thus 22

PID controller Plant The closed-loop transfer function with the PID controller is Now let us examine the unit-step response of the closedloop system to see if it exhibits approximately 25% maximum overshoot. >>num = [6. 3223 18 12. 811]; >>den = [1 6 11. 3223 18 12. 811]; >>step(num, den) >>grid 23

The maximum overshoot is about 62% and is excessive with respect to the requirement of 25%. 24

The amount of maximum overshoot can be reduced by fine tuning the parameters of the PID controller. Such fine tuning can be made on the computer. Move the pole locations The maximum overshoot is reduced to 18%. Increase the gain The speed of response is increased and the maximum overshoot is also increased to 28%. 25

The parameters of the PID controller after fine tuning Compared with the parameters obtained by Ziegler. Nichols’ second method The new ones are approximately twice the values suggested by Ziegler-Nichols’s method. Note that the Ziegler-Nichols’ tuning rule has provided a starting point for fine tuning. 26

Example ---PID Controller for DC Motor n n n Plant---Armature-controlled DC motor; MOTOMATIC system produced by Electro. Craft Corporation Design a Type A PID controller and simulate the behavior of the closed-loop system; plot the closed-loop system step response Fine tune the controller parameters so that the max overshoot is 25% or less 27

Modeling the Armature Controlled DC Motor 28

Transfer Function of the DC Motor System n Transfer function of the DC motor where C(s) is the angular displacement of the motor shaft and U(s) is the armature voltage 29

Tuning the Controller Using the Second Method of Ziegler and Nichols n Use the Routh-Hurwitz stability test; n Determine n Compute the controller parameters 30

Generating the Step Response t=0: 0. 00005: . 017; K_cr=12. 28; P_cr=135; K=0. 075*K_cr*P_cr; a=4/P_cr; num 1=K*[1 2*a a^2]; den 1=[0 1 0]; tf 1=tf(num 1, den 1); num 2=[0 0 0 0. 1464]; den 2=[7. 89 e-007 8. 25 e-004 0. 00172 0]; tf 2=tf(num 2, den 2); tf 3=tf 1*tf 2; sys=feedback(tf 3, 1); y=step(sys, t); m=max(y); Plot(t, y); 31

32

Example 2 (Based on Ex. 10 -3 in Ogata, 2002) n n Use a computational approach to generate an optimal set of the DC motor PID controller’s parameters Generate the step response of the closedloop system 33 33

Optimizing PID Parameters t=0: 0. 0002: 0. 02; for K=5: -0. 2: 2 %Outer loop to vary the values of %the gain K for a=1: -0. 01: 0. 01; %Outer loop to vary the %values of the parameter a num 1=K*[1 2*a a^2]; den 1=[0 1 0]; tf 1=tf(num 1, den 1); num 2=[0 0 0 0. 1464]; den 2=[7. 89 e-007 8. 25 e-004 0. 00172 0]; tf 2=tf(num 2, den 2); tf 3=tf 1*tf 2; sys=feedback(tf 3, 1); y=step(sys, t); m=max(y); if m<1. 1 & m>1. 05; plot(t, y); grid; sol=[K; a; m] break % Breaks the inner loop end if m<1. 1 & m>1. 05; break; %Breaks the outer loop end 34

sol=[K a m]=4. 20 1. 09 35

Tips for Designing a PID Controller 1. Obtain an open-loop response and determine what needs to be improved 2. Add a proportional control to improve the rise time 3. Add a derivative control to improve the overshoot 4. Add an integral control to eliminate the steady-state error 5. Adjust each of Kp, Ki, and Kd until you obtain a desired overall response. Lastly, please keep in mind that you do not need to implement all three controllers (proportional, derivative, and integral) into a single system, if not necessary. For example, if a PI controller gives a good enough response (like the above example), then you don't need to implement derivative controller to the system. Keep the controller as simple as 36 possible.

37

Transfer function: 38

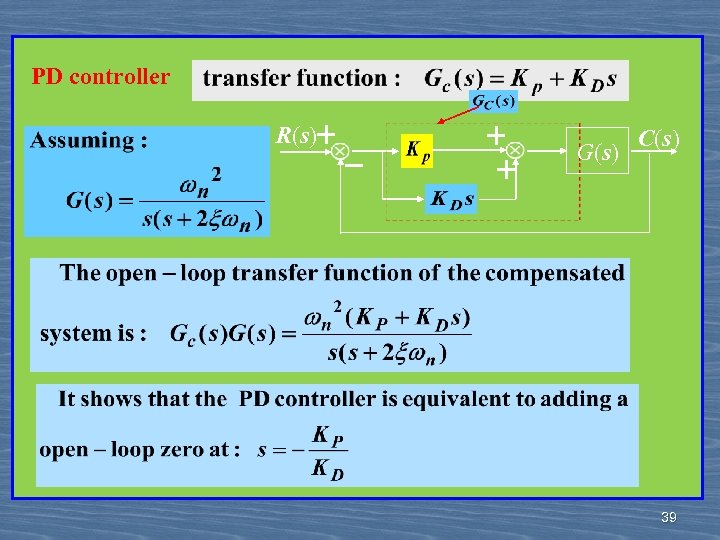PD controller R(s)＋ － ＋ ＋ G(s) C(s) 39

Effects of PD controller: 1) PD controller does not alter the system type; 2) PD controller improve the system’s stability (to increase damping and reduce maximum overshoot); 3) PD controller reduce the rise time and settling time; 4) PD controller increase BW(Band Width) 40 40

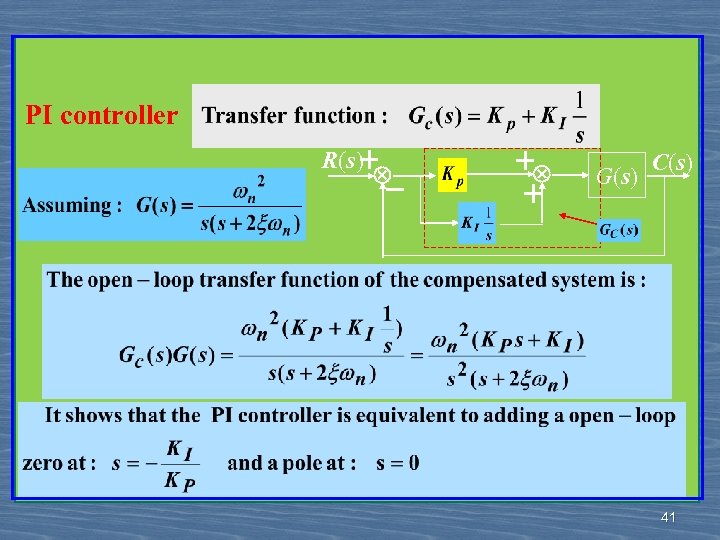PI controller R(s) ＋ － ＋ ＋ G(s) C(s) 41

Effects of PI controller: 1) Increase the system’s type－clear the steady-state error ; 2) reduce BW(Band Width) beneficial to the noise limiting , not beneficial to the system’s stability. 42

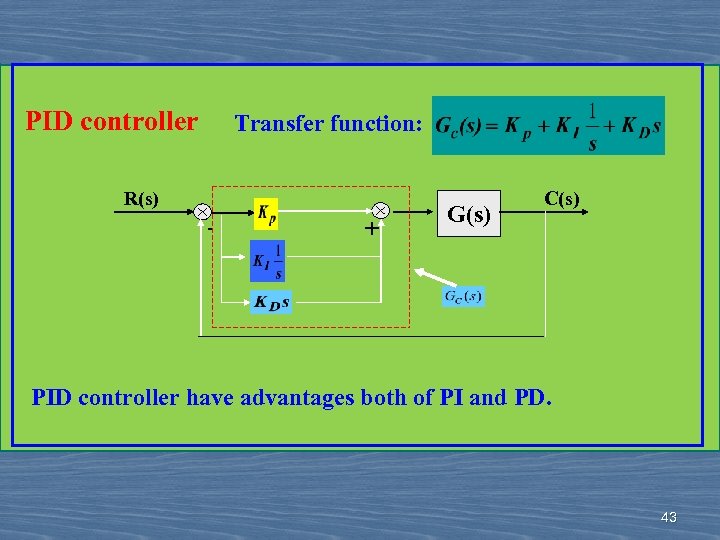PID controller Transfer function: R(s) - + G(s) C(s) PID controller have advantages both of PI and PD. 43

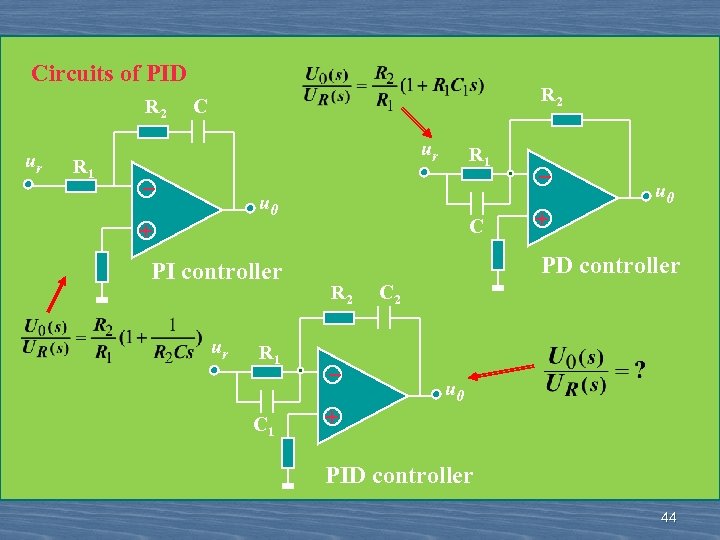Circuits of PID R 2 ur R 1 R 2 C ur _ R 1 u 0 + PI controller ur R 1 C _ + u 0 PD controller R 2 C 2 _ + u 0 PID controller 44

Effect of Control Actions n n n Proportional Action n Adjustable gain (amplifier) Integral Action n Eliminates bias (steady-state error) n Can cause oscillations Derivative Action (“rate control”) n Effective in transient periods n Provides faster response (higher sensitivity) n Never used alone 45

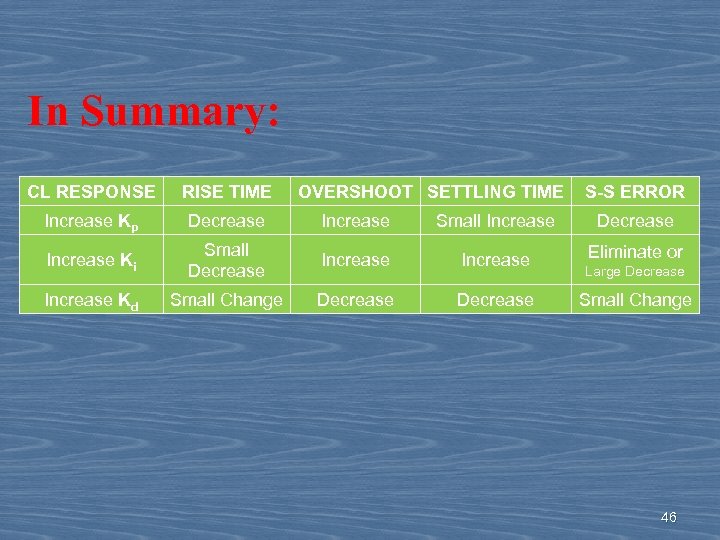In Summary: CL RESPONSE RISE TIME OVERSHOOT SETTLING TIME S-S ERROR Increase Kp Decrease Increase Small Increase Decrease Increase Ki Small Decrease Increase Eliminate or Increase Kd Small Change Decrease Large Decrease Small Change 46

Questions? Discussion? Suggestions ? 47

48