Double feature Yuri Levin Leiden 1 The theory

Double feature: Yuri Levin, Leiden 1. The theory of fast oscillations during magnetar giant flares 2. Measuring gravitational waves using Pulsar Timing Arrays

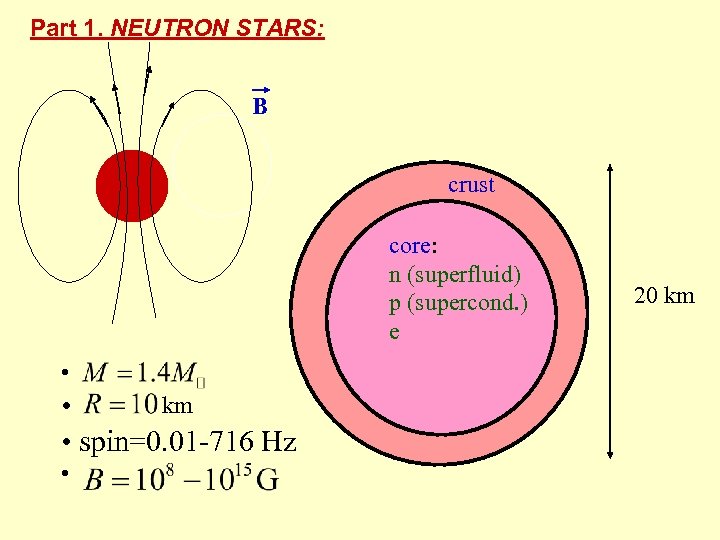
Part 1. NEUTRON STARS: B crust core: n (superfluid) p (supercond. ) e • km • • spin=0. 01 -716 Hz • 20 km

Physics preliminaries: magnetic fields in non-resistive media Field lines: B 1. Are frozen into the medium 2. Possess tension and pressure ~B 2 Alfven waves!

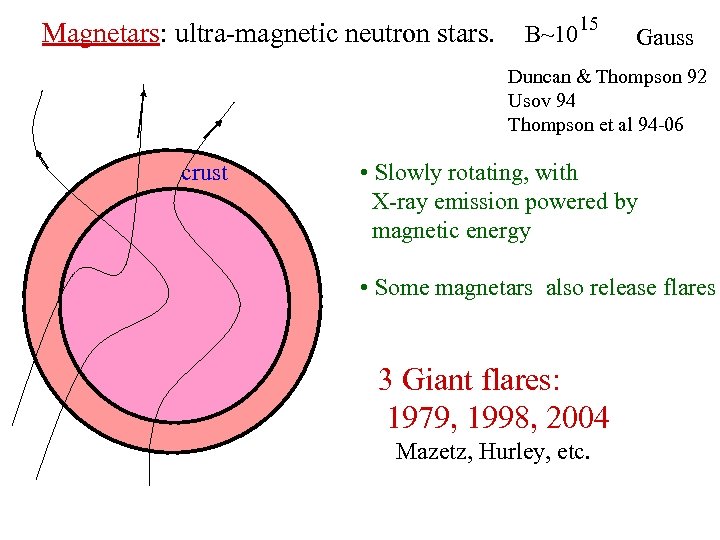
Magnetars: ultra-magnetic neutron stars. B~1015 Gauss Duncan & Thompson 92 Usov 94 Thompson et al 94 -06 crust • Slowly rotating, with X-ray emission powered by magnetic energy • Some magnetars also release flares 3 Giant flares: 1979, 1998, 2004 Mazetz, Hurley, etc.

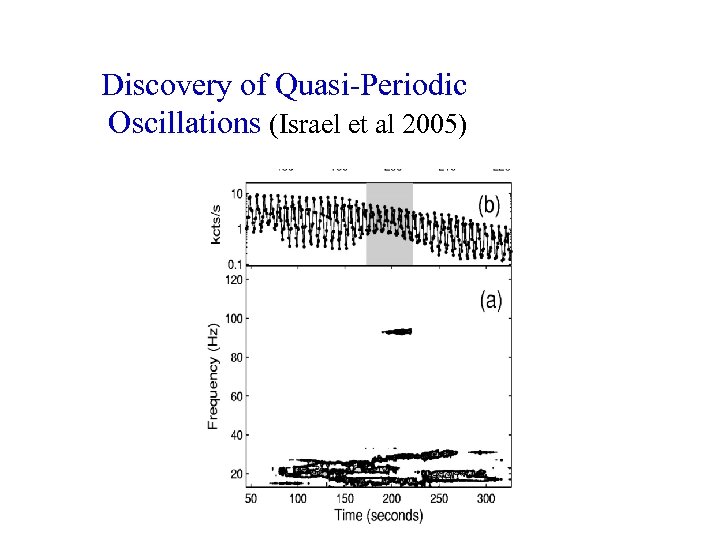
Discovery of Quasi-Periodic Oscillations (Israel et al 2005)

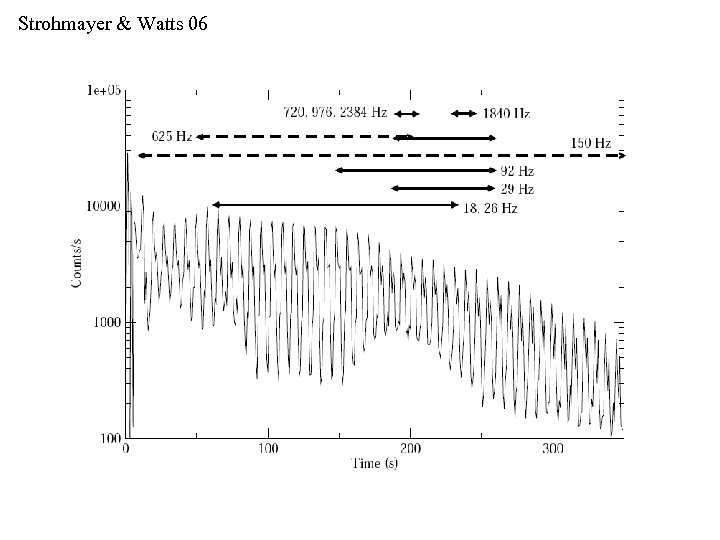
Strohmayer & Watts 06

Oscilations at several frequencies: 18, 30, 40, 90, 625, etc. , Hz. Israel et al 05 Barat et al 83 Watts & Strohmayer 06 Strohmayer & Watts 06 Interpretation 0: torsional vibration of the neutron star crust (starquake!) Duncan, et al 98 -06 Three caveats: • 18 Hz does not work • QPOs highly intermittent • Physics does not work Key issue: high B-field

Torsional vibration of the whole star L. 06, L. 07, MNRAS also Glampedakis et 06 1. Magnetically coupling to the core on 0. 01 -0. 1 second timescale. Pure crustal modes don’t exist. 2. Alfven continuum in the core. Initial crustal modes decay in <second What happens then? crust • Normal-mode analysis: global torsional mode most likely doesn’t exist

Crust-core dynamics: 1. Magnetically coupling to the core on 0. 01 -0. 1 second timescale. Pure crustal modes don’t exist. 2. Alfven continuum in the core. Initial crustal displacements decay in <second What happens then? crust • Normal-mode analysis: global torsional mode likely don’t exist • Resonant absorption, cf. solar corona (Ionson 78, Hollweg 87, Steinolfson 85, etc…. . ) Resonant Layer

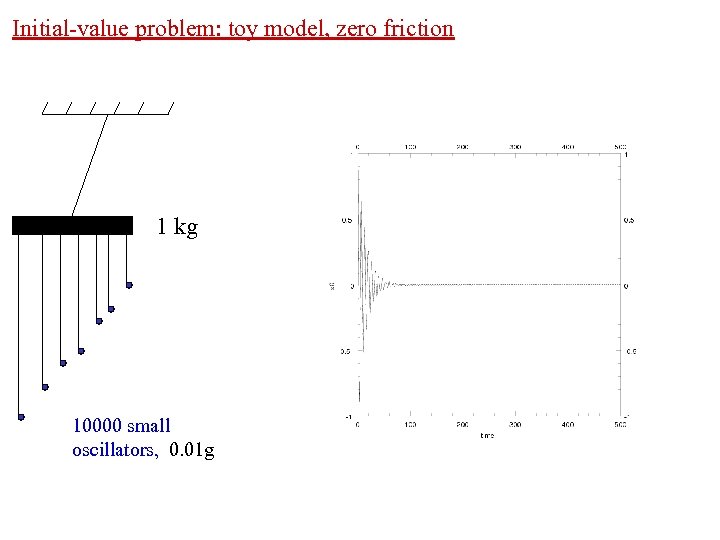
Initial-value problem: toy model, zero friction 1 kg 10000 small oscillators, 0. 01 g

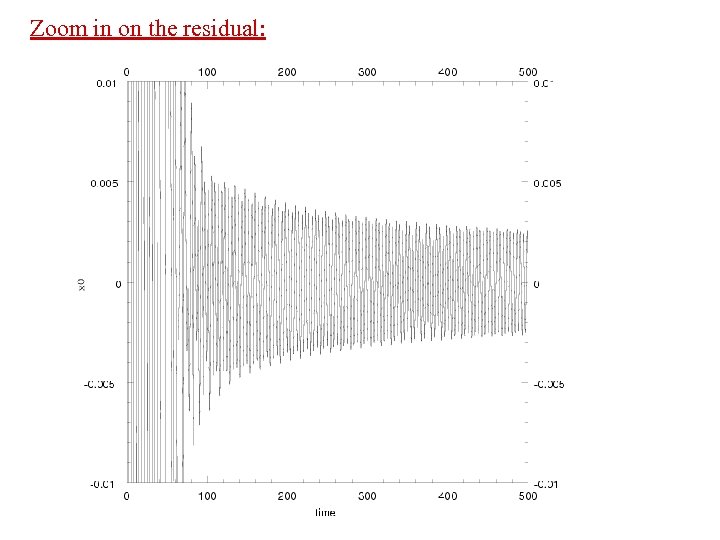
Zoom in on the residual:

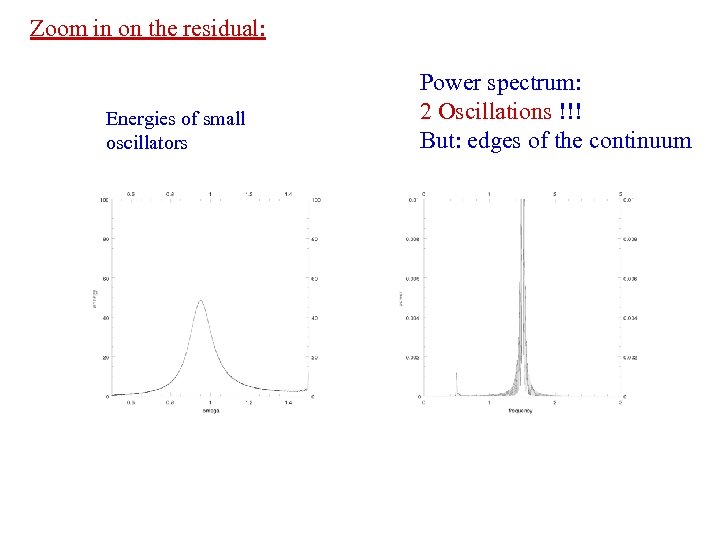
Zoom in on the residual: Energies of small oscillators Power spectrum: 2 Oscillations !!! But: edges of the continuum

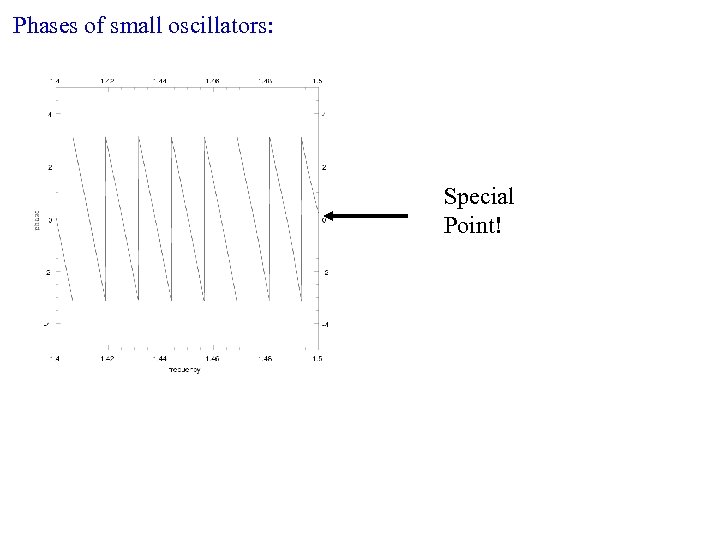
Phases of small oscillators: Special Point!

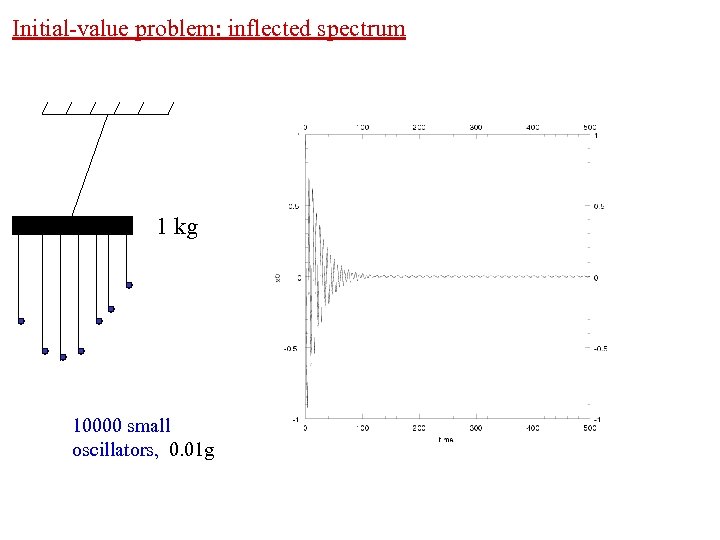
Initial-value problem: inflected spectrum 1 kg 10000 small oscillators, 0. 01 g

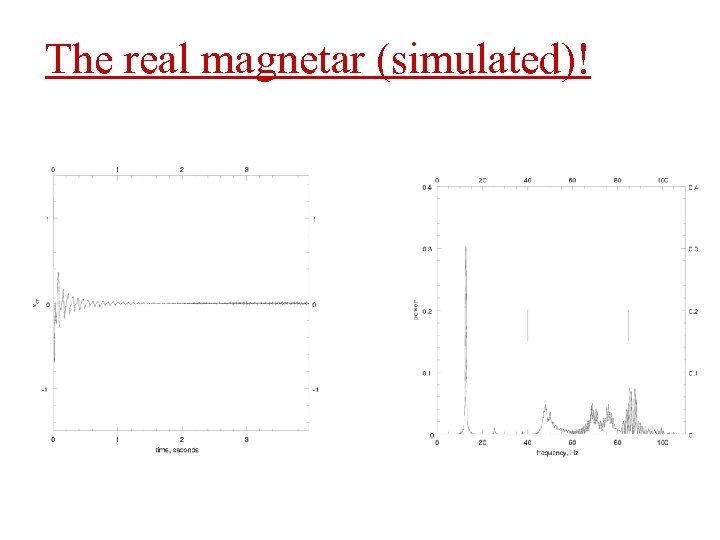
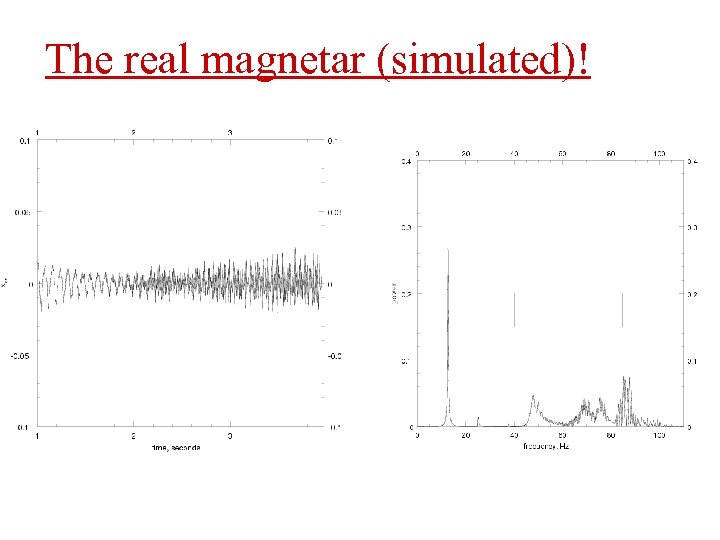
The real magnetar (simulated)!

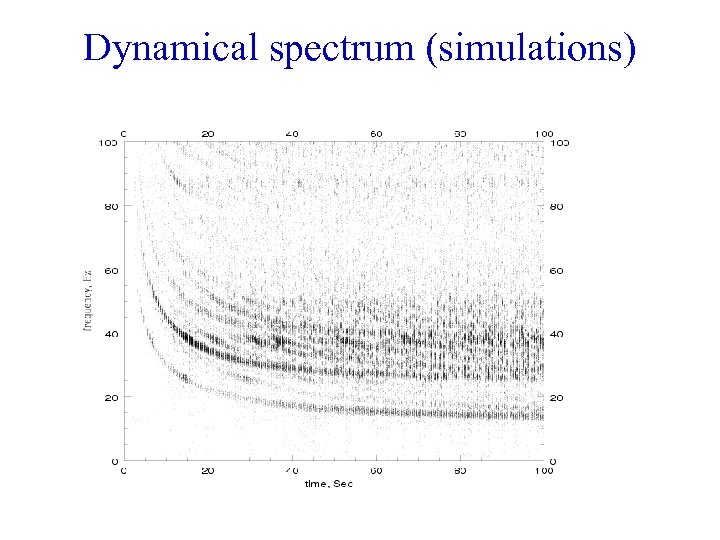
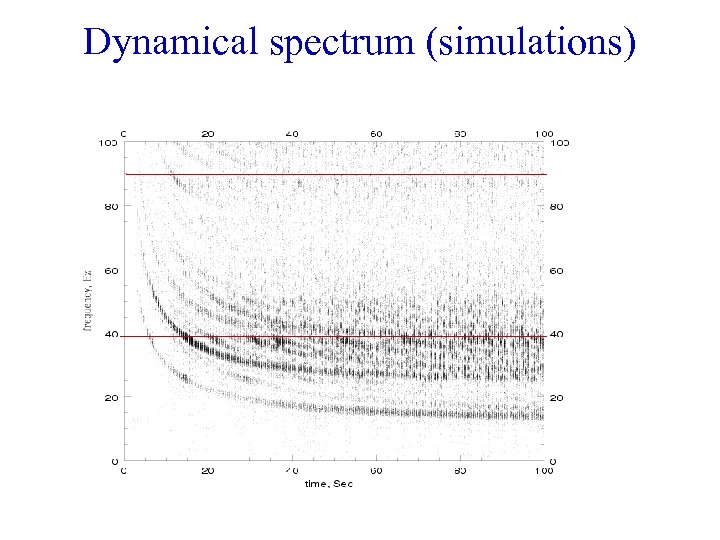
Dynamical spectrum (simulations)

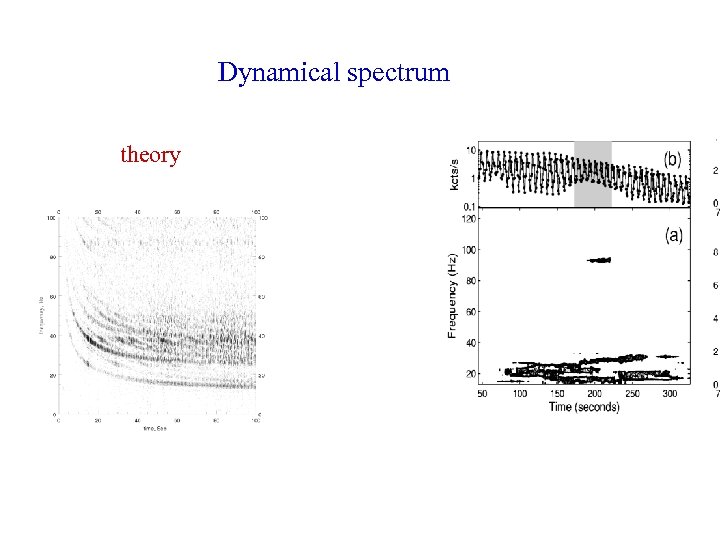
Dynamical spectrum theory

Asteroseismology? • Low-frequency QPOs (18 Hz) probe Alfven speed in the core. 15 • For B=10 G, need to decouple 90% of the core material from the wave. Neutron superfluidity!

Conclusions: main features of Quasi-Periodic Oscillations 1. Steady QPOs---special points of the Alfven continuum, 2. Intermittent QPOs everywhere, but enhanced near crustal frequencies. 3. Qualitative agreement between theory and observations 4. Powerful probe of the Alfven speed in the interior of magnetars 5. Open issue: magnetosphere

Part 2 Measuring gravitational waves using Pulsar Timing Arrays.

Galaxy formation: White & Rees 78 Universe becomes matter-dominated at z=10000. Gravitational instability becomes effective. Small halos collapse first, small galaxies form first Smaler galaxies merge to form large spirals and ellipticals.

Merging Galaxies Snijders & van der Werf 06 Merging SBHs? Komossa et al 02 (Chandra)

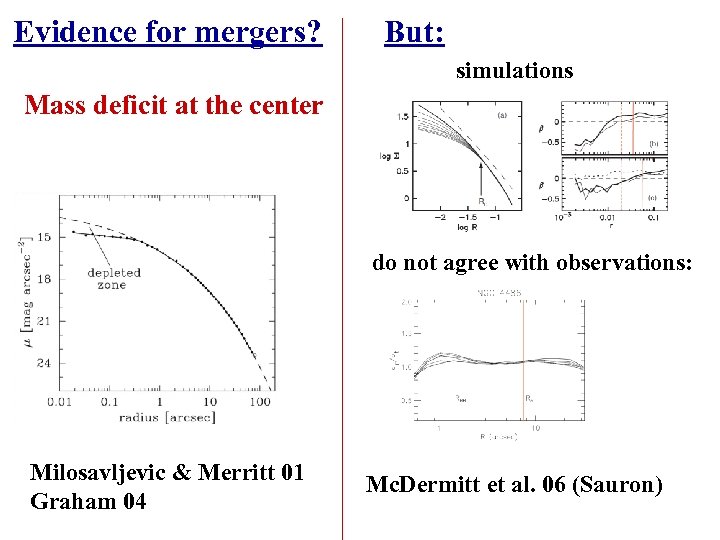
Evidence for mergers? But: simulations Mass deficit at the center do not agree with observations: Milosavljevic & Merritt 01 Graham 04 Mc. Dermitt et al. 06 (Sauron)

Q: What to do? A: Measure gravitational waves!

LISA: the ESA/NASA space mission to detect gravitational waves. Binary black hole mergers Out to z=3 is one of the main targets Launch date 1915+. .

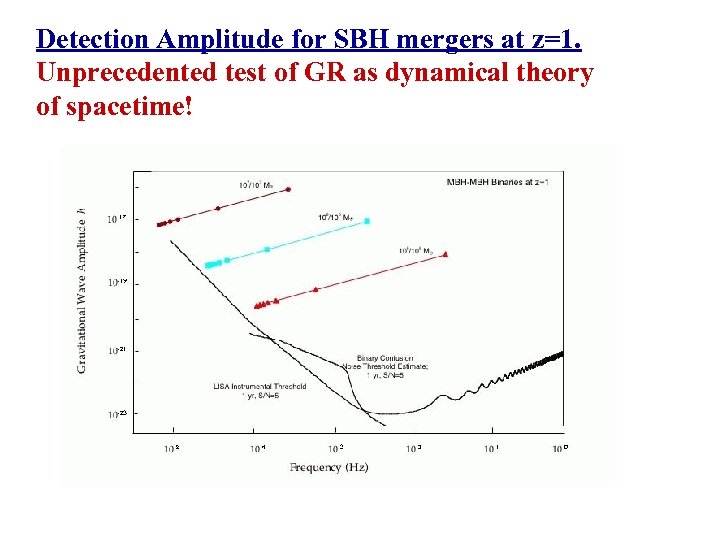
Detection Amplitude for SBH mergers at z=1. Unprecedented test of GR as dynamical theory of spacetime!

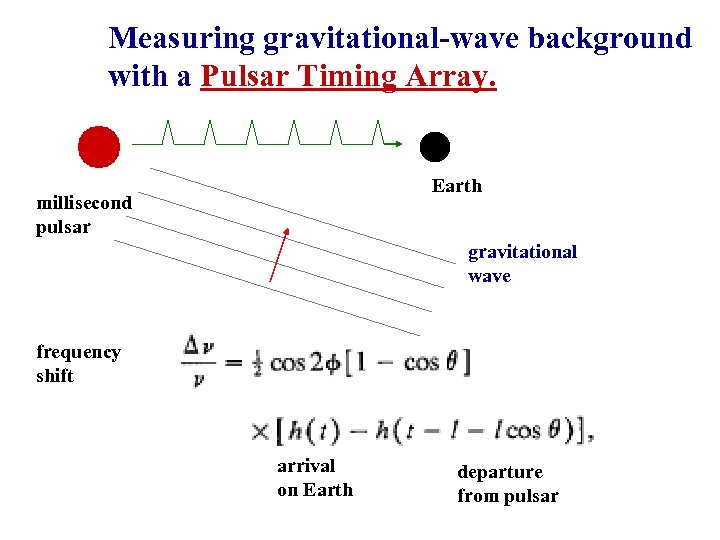
Measuring gravitational-wave background with a Pulsar Timing Array. Earth millisecond pulsar gravitational wave frequency shift arrival on Earth departure from pulsar

Millisecond pulsars: • Excellent clocks. Current precision 1 microsecond, projected precision ~100 -200 ns. • Intrinsic noise unknown and uncorrelated. GW noise uknown but correlated. Thus need to look for correlations between different pulsars. Many systematic effects with correlations: local noisy clocks, ephemeris errors, etc. However, GW signature is unique! 2 Pulsar Timing Arrays: Australia (20 pulsars) Europe (~20) Manchester Kramer+ Stappers

John Rowe animation/ATNF, CSIRO

Contributions to timing residuals: • Gravitational waves!! • Pulsar timing noises • Quadratic spindowns • Variations in the ISM • Clock noises • Earth ephemeris errors • Changes of equipment • Human errors • Our work so far Optimistic esimate: ~5000 timing residuals from all pulsars.

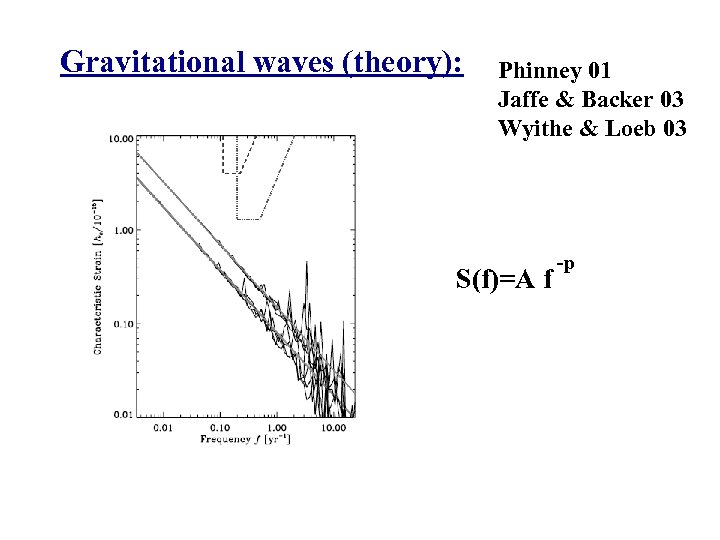
Gravitational waves (theory): Phinney 01 Jaffe & Backer 03 Wyithe & Loeb 03 S(f)=A f -p

Current algorithm Jenet et al. 05 • <δt a δt b> = const·[6 x log(x)-x+2], GW pulsar a pulsar b x=cos(ab) Look for correlation of this form! But: statistical significance? Parameter extraction?

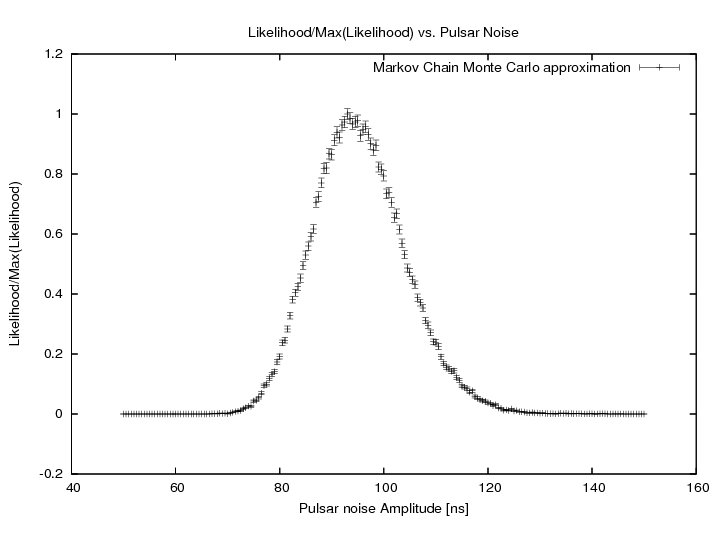
Leiden+CITA effort: Gravitational-Wave signal extraction van Haasteren, L. , Mc. Donald (CITA), Lu (CITA), soon tbs Bayesian approach: • Parametrize simultaneously GW background and pulsar noises (42 parameters) • Parametrize quadratic spindowns (60 parameters) • derive P(parameters|data), where data=5000 timing residuals • marginalize numerically over pulsar noises and analytically over the spindowns

Advantages • No loss of information-optimal detection • Measures the amplitude AND the slope of GWB • Natural treatment of known systematic errors • Allows unevenly sampled data

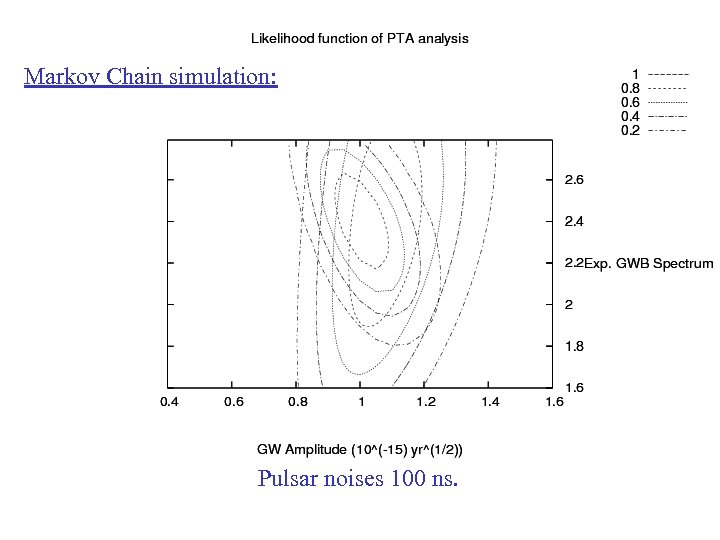
Markov Chain simulation: Pulsar noises 100 ns.

Conclusions part 2: • SBH binaries predicted but not yet observed • Gravitational-wave detection by LISA and Pulsar-Timing Arrays is likely within 1 -1. 5 decade.

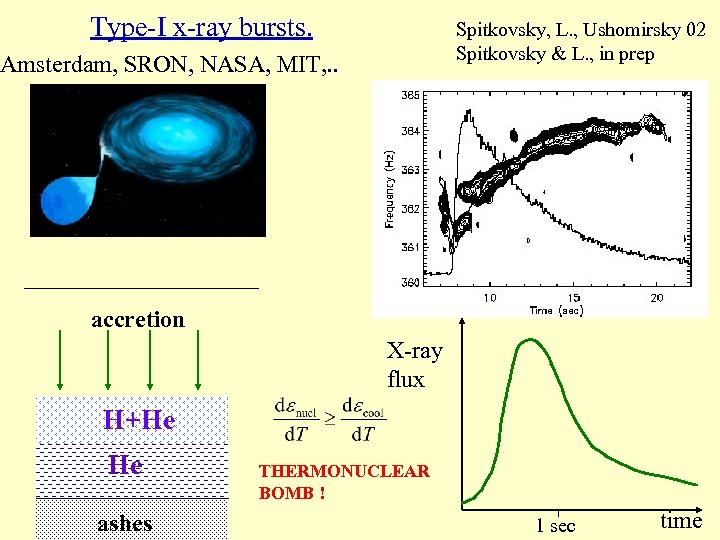
Type-I x-ray bursts. Spitkovsky, L. , Ushomirsky 02 Spitkovsky & L. , in prep Amsterdam, SRON, NASA, MIT, . . accretion X-ray flux H+He He ashes THERMONUCLEAR BOMB ! 1 sec time

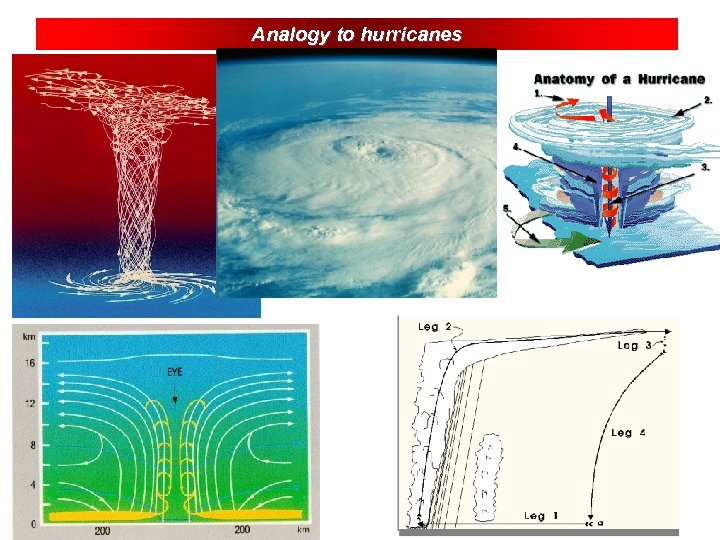
Analogy to hurricanes

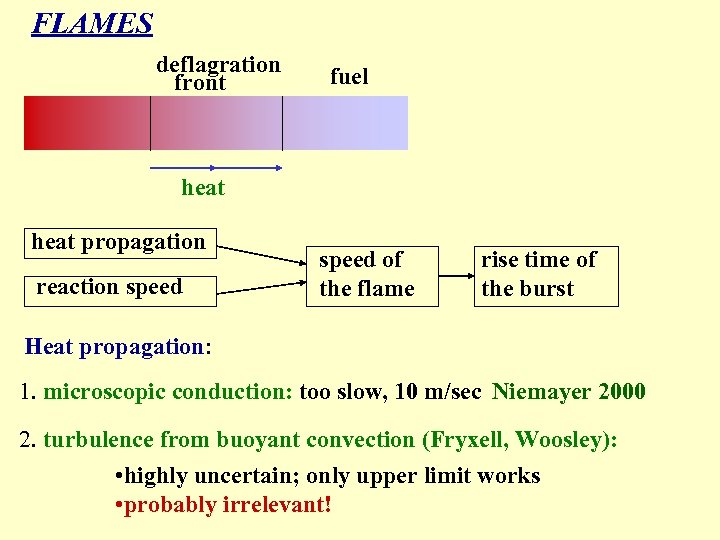
FLAMES deflagration front fuel heat propagation reaction speed of the flame rise time of the burst Heat propagation: 1. microscopic conduction: too slow, 10 m/sec Niemayer 2000 2. turbulence from buoyant convection (Fryxell, Woosley): • highly uncertain; only upper limit works • probably irrelevant!

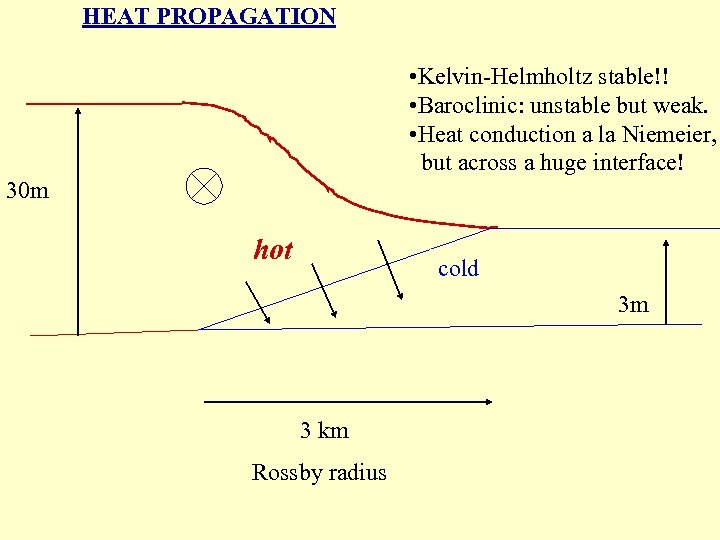
HEAT PROPAGATION • Kelvin-Helmholtz stable!! • Baroclinic: unstable but weak. • Heat conduction a la Niemeier, but across a huge interface! 30 m hot cold 3 m 3 km Rossby radius

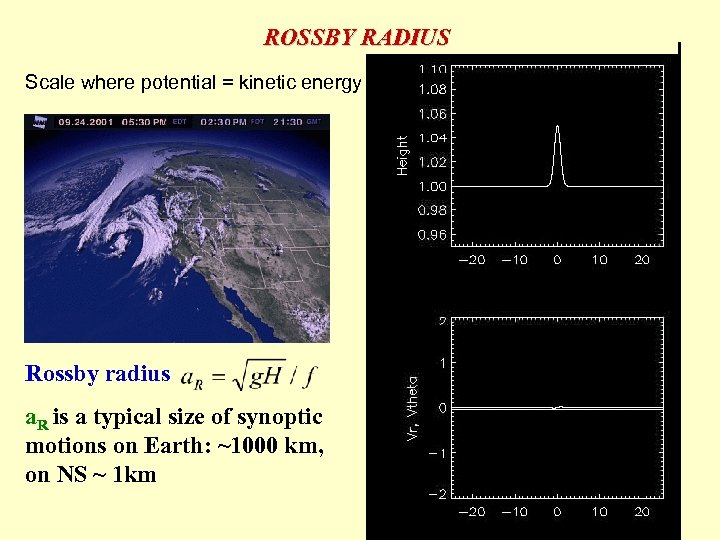
ROSSBY RADIUS Scale where potential = kinetic energy Rossby radius a. R is a typical size of synoptic motions on Earth: ~1000 km, on NS ~ 1 km

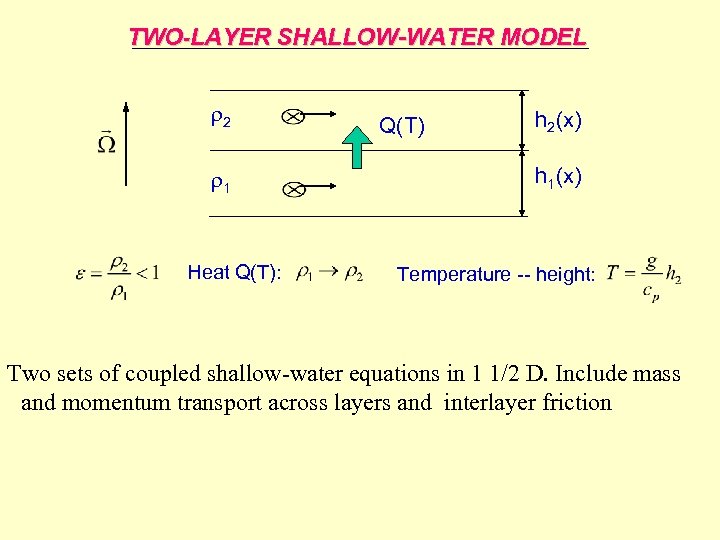
TWO-LAYER SHALLOW-WATER MODEL 2 1 Heat Q(T): Q(T) h 2(x) h 1(x) Temperature -- height: Two sets of coupled shallow-water equations in 1 1/2 D. Include mass and momentum transport across layers and interlayer friction

Burst QPOs from ocean Rossby waves? + QPO coherence, + QPOs in the tail Heyl 2004, Lee 2005, Piro & Bildsten 2005, Narayan & Cooper 2007 - Typically, waves go too fast. - Not clear how to excite them. - What happens during the burst rise (i. e. , spreading hot spot)?

Conclusions: 1. Good prospects to understand magnetar QPOs and 2. to learn about neutron-star interior 2. Good prospects to understand type-I burst deflagration, but QPO behaviour, etc. , very difficult to understand

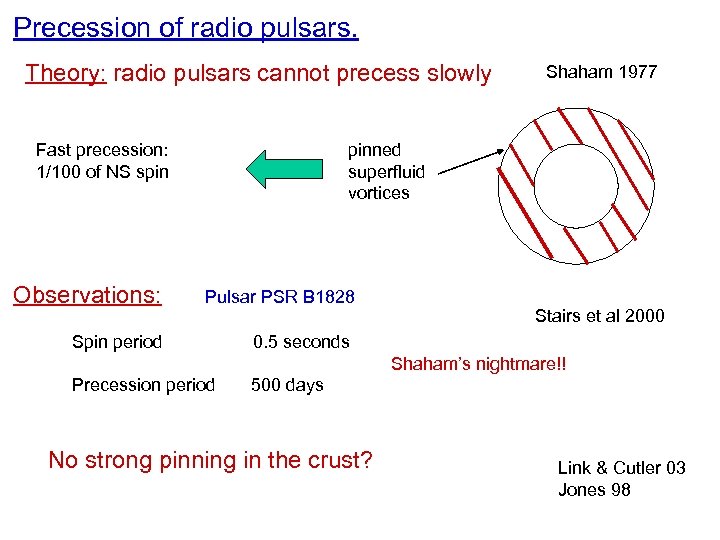
Precession of radio pulsars. Theory: radio pulsars cannot precess slowly Fast precession: 1/100 of NS spin Observations: Shaham 1977 pinned superfluid vortices Pulsar PSR B 1828 Spin period Stairs et al 2000 0. 5 seconds Shaham’s nightmare!! Precession period 500 days No strong pinning in the crust? Link & Cutler 03 Jones 98

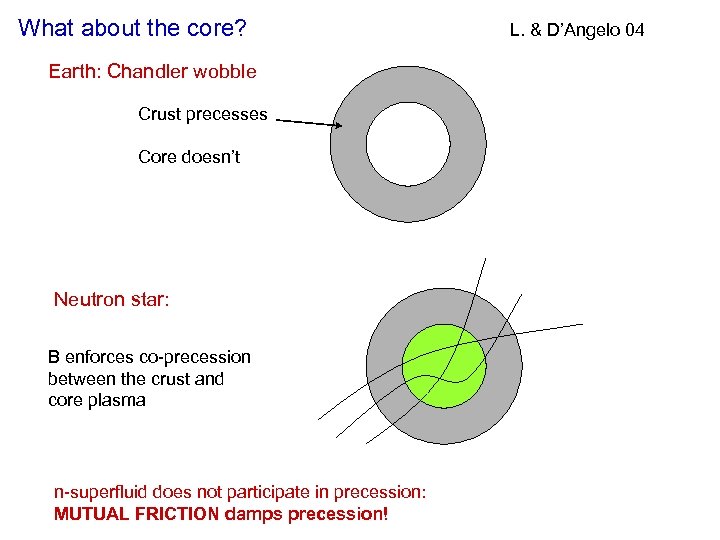
What about the core? Earth: Chandler wobble Crust precesses Core doesn’t Neutron star: B enforces co-precession between the crust and core plasma n-superfluid does not participate in precession: MUTUAL FRICTION damps precession! L. & D’Angelo 04

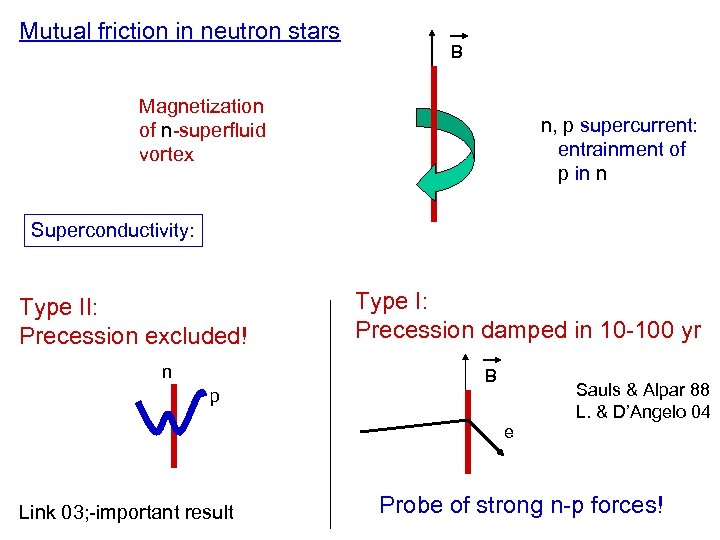
Mutual friction in neutron stars B Magnetization of n-superfluid vortex n, p supercurrent: entrainment of p in n Superconductivity: Type II: Precession excluded! n p Type I: Precession damped in 10 -100 yr B Sauls & Alpar 88 L. & D’Angelo 04 e Link 03; -important result Probe of strong n-p forces!

Spitkovsky

Formation of a neutron star: Burrows, Livne, et al. 2006