Скачать презентацию ДОСТАВКА ГРУЗА В КРОТЧАЙШИЙ СРОК Введение В Скачать презентацию ДОСТАВКА ГРУЗА В КРОТЧАЙШИЙ СРОК Введение В

Кокотеев курсовая защита.pptx

  • Количество слайдов: 15

ДОСТАВКА ГРУЗА В КРОТЧАЙШИЙ СРОК ДОСТАВКА ГРУЗА В КРОТЧАЙШИЙ СРОК

Введение В практической деятельности могут возникнуть ситуации, когда нас в первую очередь интересуют не Введение В практической деятельности могут возникнуть ситуации, когда нас в первую очередь интересуют не затраты на перевозку груза (их минимизация), а время доставки этих грузов потребителям. Например, при подготовке крупных военных операций, когда необходимо в кратчайший срок сосредоточить ресурсы в намеченных пунктах или при стихийных бедствиях, возникает задача обеспечения пострадавших районов различными ресурсами в кратчайший срок.

Специальный алгоритм 1. Любым способом строим один из опорных планов. 2. Определяем наибольший элемент Специальный алгоритм 1. Любым способом строим один из опорных планов. 2. Определяем наибольший элемент t' из всех tij, соответствующих занятым клеткам, и все клетки с элементами tij ≥ t' (это могут быть лишь свободные клетки) вычеркиваются.

Специальный алгоритм 3. Начиная с клетки с наибольшим временем доставки t' строим разгрузочный цикл Специальный алгоритм 3. Начиная с клетки с наибольшим временем доставки t' строим разгрузочный цикл так, чтобы клетки с нечетными номерами (считая первой разгружаемую клетку с элементом t') были занятыми. Одна из вершин разгрузочного цикла будет свободной. В общем случае построение разгрузочного цикла неоднозначно. 4. Сделав в свободную вершину цикла поставку p, проводим компенсации по вершинам цикла, определяем величину р (так же, как в методе потенциалов), строим новый план.

Специальный алгоритм 5. Переходим ко второму пункту алгоритма, естественно, не учитывая ранее вычеркнутые клетки. Специальный алгоритм 5. Переходим ко второму пункту алгоритма, естественно, не учитывая ранее вычеркнутые клетки. 6. Алгоритмом пользуемся до тех пор, пока построение разгрузочного цикла становится невозможным. 7. Последний полученный план является оптимальным, наибольшее время, соответствующее занятой клетке в этом плане, определяет наименьшее время по доставке грузов всем потребителям.

Пример Определить оптимальный план перевозок из условия доставки груза в кратчайший срок. Известны ресурсы Пример Определить оптимальный план перевозок из условия доставки груза в кратчайший срок. Известны ресурсы аi. 30; 35; 40, потребности bk: 20; 34; 16; 10; 25 и матрица где tik — время, затрачиваемое на перевозку груза из i го пункта отправления в k й пункт назначения.

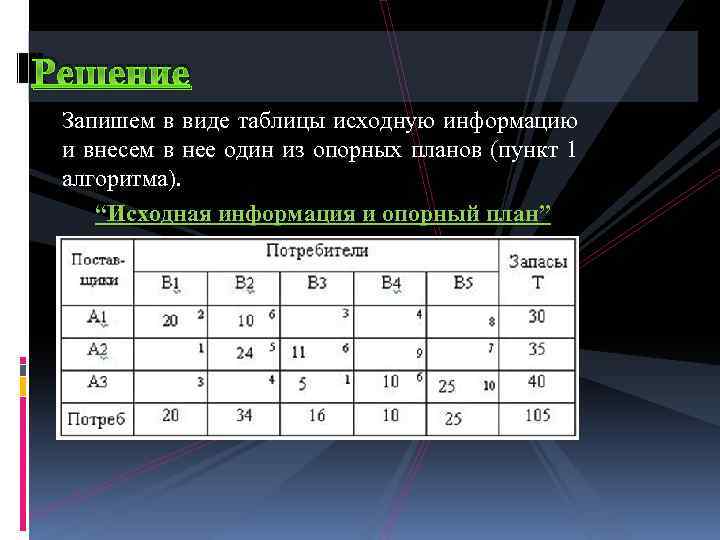Решение Запишем в виде таблицы исходную информацию и внесем в нее один из опорных Решение Запишем в виде таблицы исходную информацию и внесем в нее один из опорных планов (пункт 1 алгоритма). “Исходная информация и опорный план”

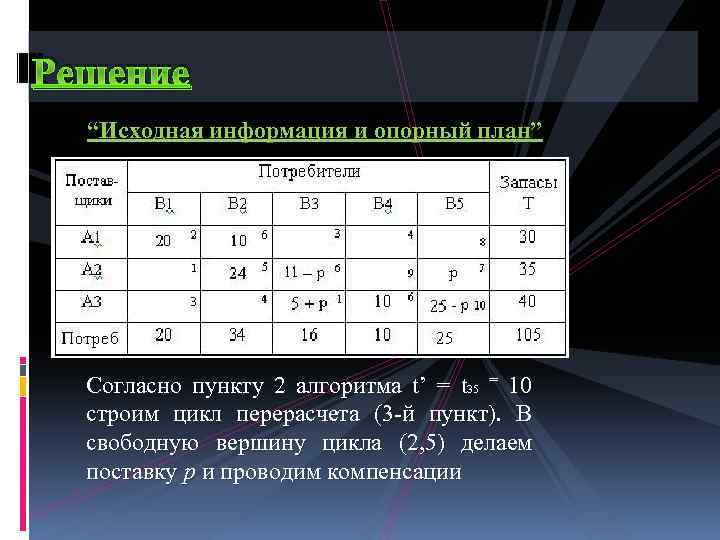Решение “Исходная информация и опорный план” Согласно пункту 2 алгоритма t’ = t 35 Решение “Исходная информация и опорный план” Согласно пункту 2 алгоритма t’ = t 35 = 10 строим цикл перерасчета (3 й пункт). В свободную вершину цикла (2, 5) делаем поставку p и проводим компенсации

Решение “Исходная информация и опорный план” по вершинам цикла, затем определяем величину p: p=11. Решение “Исходная информация и опорный план” по вершинам цикла, затем определяем величину p: p=11.

Решение Строим новый план и переходим к пункту 2 алгоритма. “Промежуточный план распределения” Решение Строим новый план и переходим к пункту 2 алгоритма. “Промежуточный план распределения”

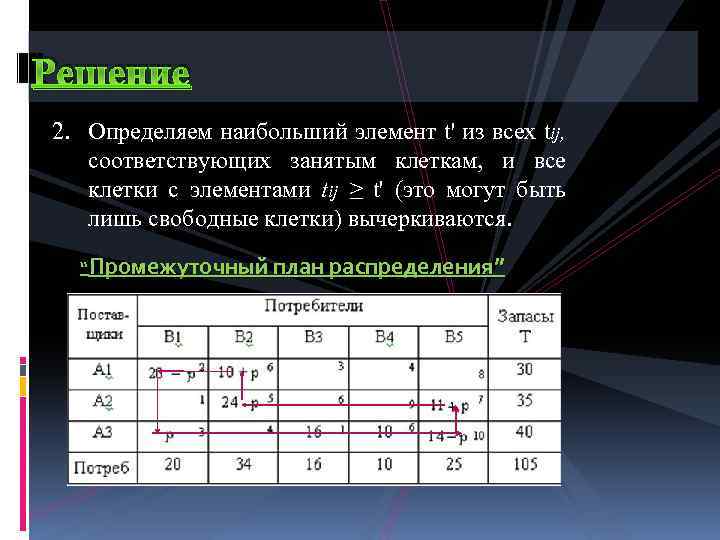Решение 2. Определяем наибольший элемент t' из всех tij, соответствующих занятым клеткам, и все Решение 2. Определяем наибольший элемент t' из всех tij, соответствующих занятым клеткам, и все клетки с элементами tij ≥ t' (это могут быть лишь свободные клетки) вычеркиваются. “Промежуточный план распределения”

Решение В новой таблице t' = t 35 =10 (клетка 3, 5 оказалась не Решение В новой таблице t' = t 35 =10 (клетка 3, 5 оказалась не полно стью разгруженной). Из анализа нового цикла пересчета заключаем: p = 14 “Промежуточный план распределения”

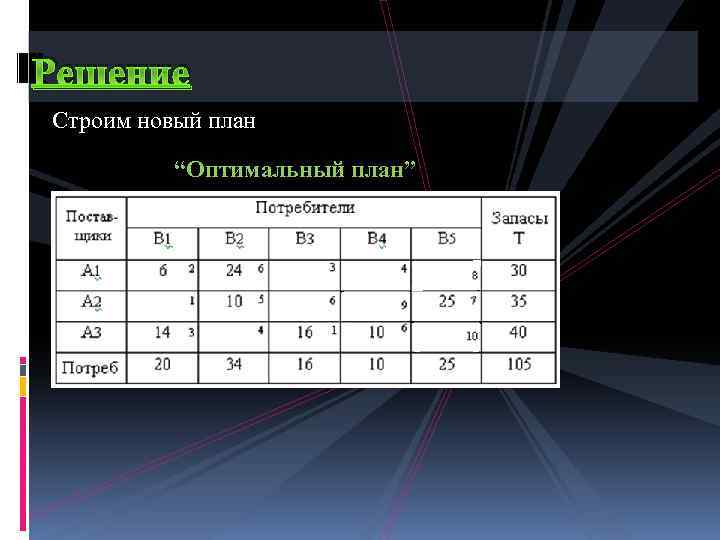Решение Строим новый план “Оптимальный план” Решение Строим новый план “Оптимальный план”

Решение “Оптимальный план” t' = t 25 ≥ 7, вычеркиваем все свободные клетки, для Решение “Оптимальный план” t' = t 25 ≥ 7, вычеркиваем все свободные клетки, для которых tij ≥ 7. Для дальнейшего улучшения плана необходимо разгрузить клетку (2, 5), но построение разгрузочного цикла для этой клетки невозможно.

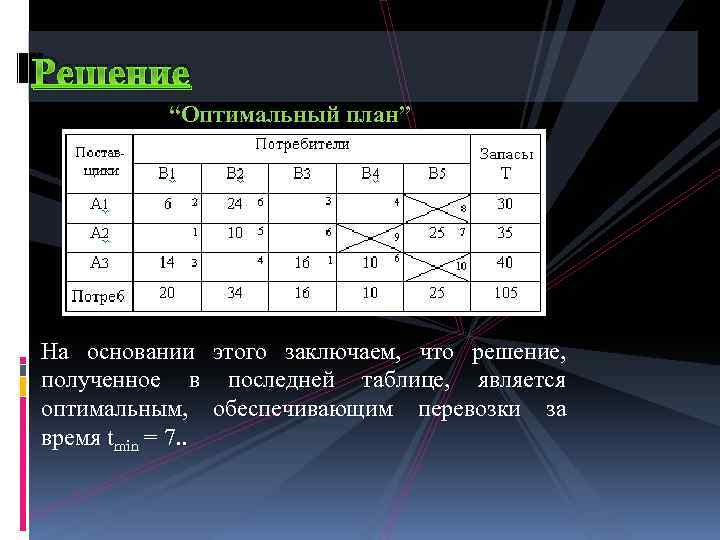Решение “Оптимальный план” На основании этого заключаем, что решение, полученное в последней таблице, является Решение “Оптимальный план” На основании этого заключаем, что решение, полученное в последней таблице, является оптимальным, обеспечивающим перевозки за время tmin = 7. .