Доминов Никита КИТ-63 АВТОМАТНЫЕ ОСНОВЫ КОМПЬЮТЕРНОЙ СХЕМОТЕХНИКИ

Доминов Никита КИТ-63 АВТОМАТНЫЕ ОСНОВЫ КОМПЬЮТЕРНОЙ СХЕМОТЕХНИКИ

Автоматом называют определённую систему, которая имеет nвходов и m-выходов и которая производит определённое преобразование множества входных сигналов A = {a 1, a 2, …, an} в множество выходных сигналов B = {b 1, b 2, …, bn}. Такой автомат можно задать шестикомпонентным вектором:

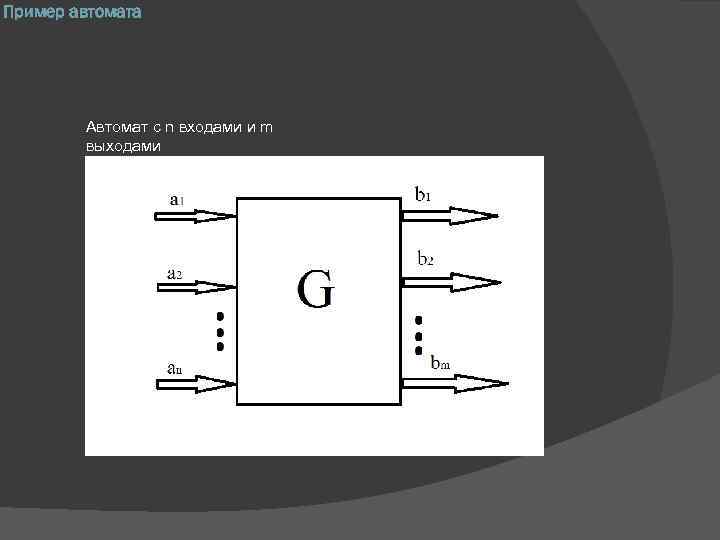Пример автомата Автомат с n входами и m выходами

Способы задавания автоматов табличный графический С помощью матрицы переходов

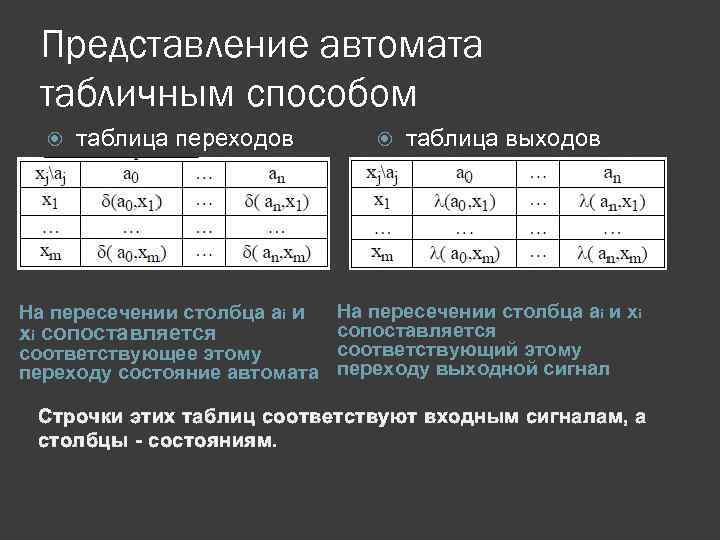Представление автомата табличным способом таблица переходов таблица выходов На пересечении столбца ai и xi сопоставляется соответствующий этому соответствующее этому переходу состояние автомата переходу выходной сигнал Строчки этих таблиц соответствуют входным сигналам, а столбцы - состояниям.

Совмещенная таблица переходов и выходов автомата Мили:

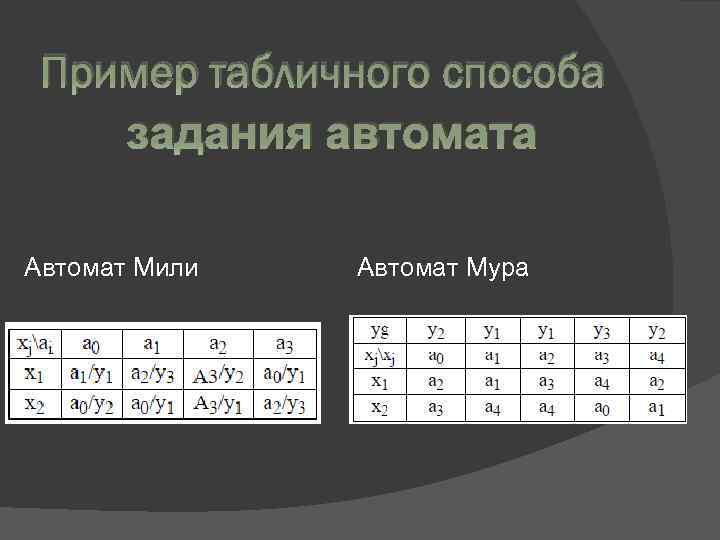Пример табличного способа задания автомата Автомат Мили Автомат Мура

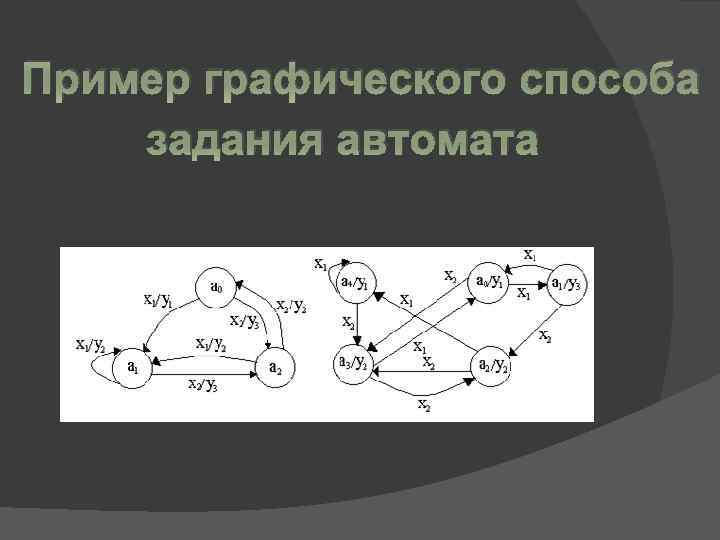Пример графического способа задания автомата

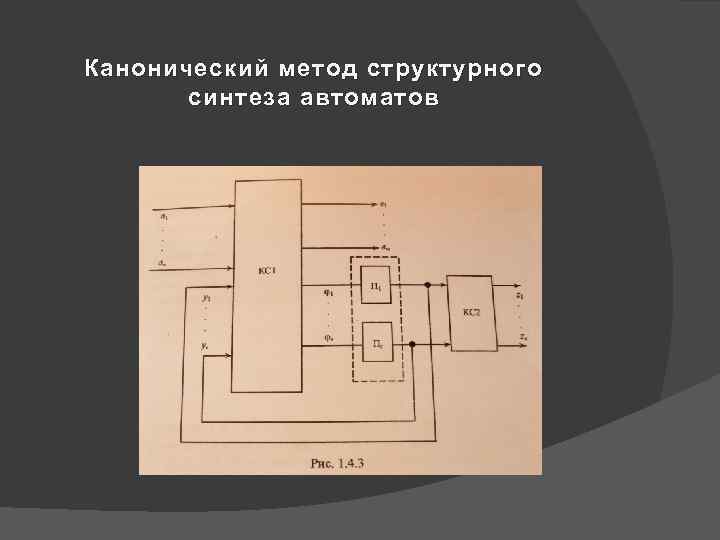Канонический метод структурного синтеза автоматов

Память автомата состоит из выбранных автоматов памяти - элементарных автоматов Мура П 1, …, Пr. После выбора элементов памяти каждое состояние абстрактного С-автомата кодируется в структурном автомате. Если все автоматы П 1, . . Пr одинаковые, то их число будет равняться: n = ] logθM [ Где: Θ - число состояний элементарного автомата памяти; M - число состояний абстрактного С-автомата; ][ - показатель того, что берётся наибольшее целое число от результата логарифма.

Синтез структурного автомата Мура на D -триггерах Основные этапы синтеза автомата: 1) Находим количество элементов памяти R >=]Log 2 M[, и кодируем состояния абстрактного автомата. 2) Кодируем входные и выходные сигналы. 3) Структурный автомат представляем обобщенной схемой. 4) Составляем закодированную таблицу выходов автомата и по ней записываем уравнения выходов. 5) Составляем закодированную таблицу переходов автомата и по ней записываем уравнения для функций возбуждения. 6) Уравнения функций возбуждения и выходов минимизируются (по картам Карно, например) и по ним строится схема в заданном функционально - логическом базисе ({И, ИЛИ, НЕ}, {И-НЕ}, {ИЛИ-НЕ} ).

Рассмотрим синтез структурного автомата Мура на D -триггерах в элементном базисе {И, ИЛИ, НЕ}. 1) Находим количество элементов памяти R = 2 и кодируем состояния абстрактного автомата. 2) Кодируем входные и выходные сигналы абстрактного автомата.

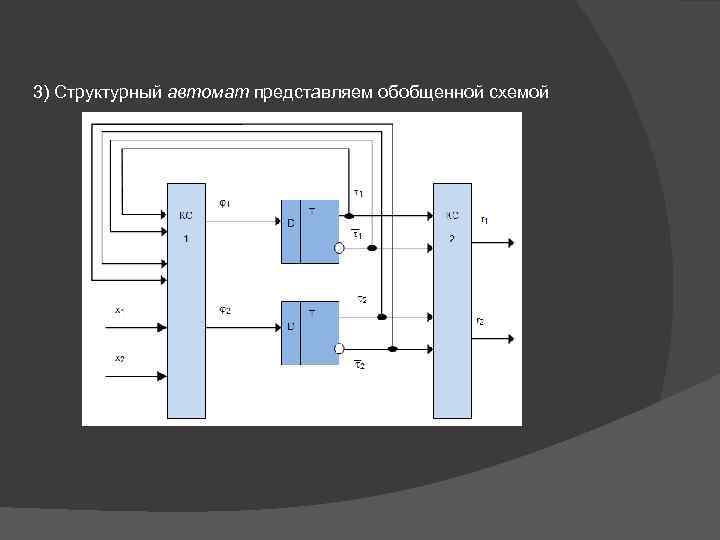3) Структурный автомат представляем обобщенной схемой

4) Представляем, используя коды состояний, входных и выходных сигналов Функция выхода r 1, зависящая для автомата Мура только от состояния, принимает единичное значение на единственном наборе 10, т. е. Функция выхода r 2, принимает единичное значение так же на единственном наборе равном 01, то есть Таким образом, уравнения выходов:

5) Записываем уравнения для функций возбуждения. Так как в D -триггере функция возбуждения совпадает с состоянием перехода, то функцию возбуждения можно записать по п 4. Находим единичные состояния первого триггера. Их всего пять. Функция возбуждения зависит от входных сигналов и состояния автомата, из которого был переключен данный триггер : Первое единичное значение функция возбуждения принимает при переходе из состояния а 0, закодированного как 00, то есть , при поступлении единичных входных сигналов . Аналогично находим остальные термы и записываем функцию возбуждения первого триггера: Для второго триггера состояний перехода, в которых он принимает единичные значения, четыре. Они выделены темно красным цветом. По ним записана функцию возбуждения второго триггера:

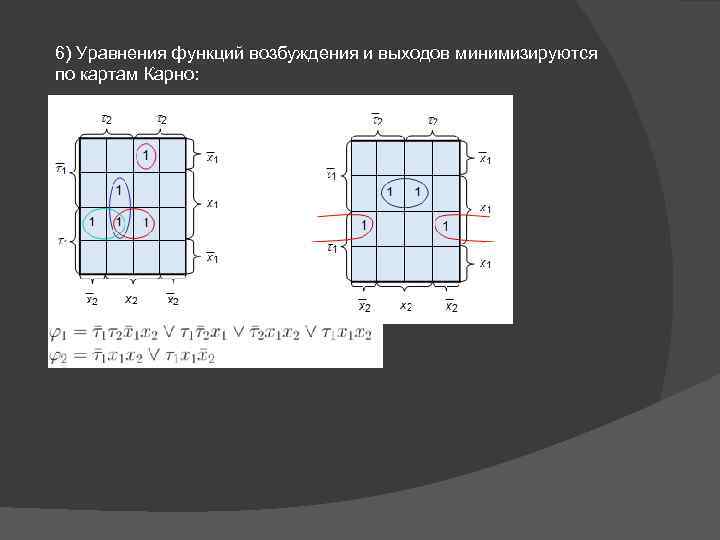6) Уравнения функций возбуждения и выходов минимизируются по картам Карно:

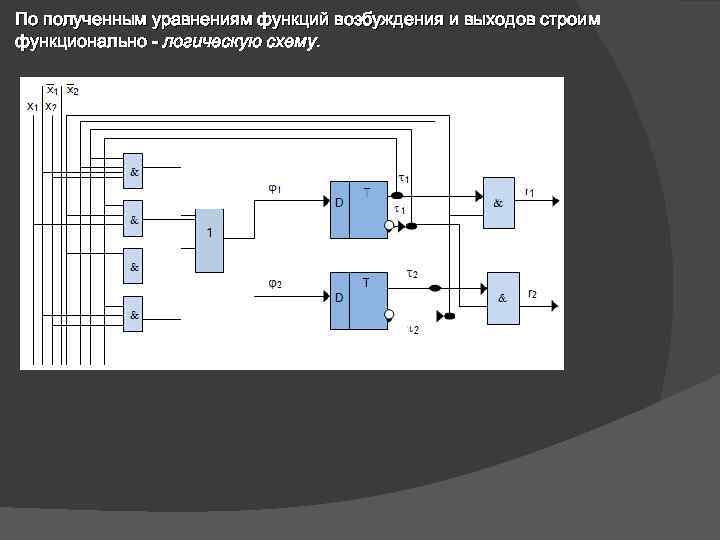По полученным уравнениям функций возбуждения и выходов строим функционально - логическую схему.