контрольная работа по логике_14_мая.pptx
- Количество слайдов: 21

Домашняя контрольная работа по теме «Логика»

• Для успешного выполнения контрольной работы вам нужно знать: - правила составления логических выражений, - правила построения таблиц истинности, - законы логики.

Рекомендации: ознакомьтесь с решением задач и выполните по аналогии предложенные задания. Переписывать условия задач не надо, укажите только номер задания и полное решение. Всего надо решить 5 задач. При решении задач средствами алгебры логики обычно используется следующая схема решения: • изучается условие задачи; • вводится система обозначений для логических высказываний; • конструируется логическая формула, описывающая логические связи между всеми высказываниями условия задачи; • определяются значения истинности этой логической формулы; • из полученных значений истинности формулы определяются значения истинности введённых логических высказываний, на основании которых делается заключение о решении.

Основные законы логики: • • • ¬¬А = А (закон двойного отрицания) ¬(А Λ В) = ¬А V ¬B ( законы ¬(А V В) = ¬А Λ ¬B Моргана) А → В = ¬А V B А Λ ¬А = 0 (закон непротиворечия) А V ¬А = 1 (закон исключенного третьего)

Основные законы логики: Законы коммутативности: • (А Λ В) ≡ (В Λ А) ; • (А V В) ≡ (В V А) ; Законы ассоциативности: • (А V В) V С ≡ А V (В V С); • (А Λ В) Λ С ≡ А Λ (В Λ С); Законы дистрибутивности: • А Λ (В V С) ≡ (А Λ В) V (А Λ С) • А V (В Λ С) ≡ (А V В) Λ (А V С)

Пример 1. Записать составное высказывание «(2· 2=5 или 2· 2=4) и (2· 2 5 или 2· 2 4)» в форме логического выражения и определить его истинность. Решение: А= « 2· 2=5» (высказывание ложно (0)) В= « 2· 2=4» (высказывание истинно (1)) «(А или В) и (А или В)» F=(A B)&(A B) Подставим значения высказываний: • F=(A B)&(A B)=(0 1)&(1 0)=1&1=1 Ответ: составное высказывание истинно.

Задача 1. • Записать составное высказывание «(2· 2=4 и 3· 3=9) или (2· 2 4 и 3· 3 9) в форме логического выражения. Определить его истинность.

Пример 2. • В нарушении правил обмена валюты подозреваются четыре работника банка А, В, С и D. Известно, что: а) если А нарушил, то и В нарушил; б) если В нарушил, то и С нарушил или А не нарушал; в) если D не нарушил, то А нарушил, а С не нарушал; г) если D нарушил, то А нарушил

Решение: Введём обозначения: А – A нарушил, В – В нарушил, С – С нарушил, D – D нарушил. Запишем каждое из высказываний а, б, в, г с помощью латинских букв и логических операций: а) А → B; б) B → C V ¬А; в) ¬D → A Λ ¬C; г) D →A Произведение всех высказываний должно быть истинным (это следует из условия задачи), то есть будет равно 1. Перемножим высказывания: ( А →B)Λ(B→ C V ¬А)Λ(¬D → A Λ ¬C)Λ (D → A) = 1 Все логические выражения соединены знаком конъюнкции, а конъюнкция нескольких выражений истинна тогда и только тогда, когда истинно каждое из выражений, то есть: А →B = 1; B →C V ¬А = 1; ¬D → A Λ ¬C = 1; D → A = 1;
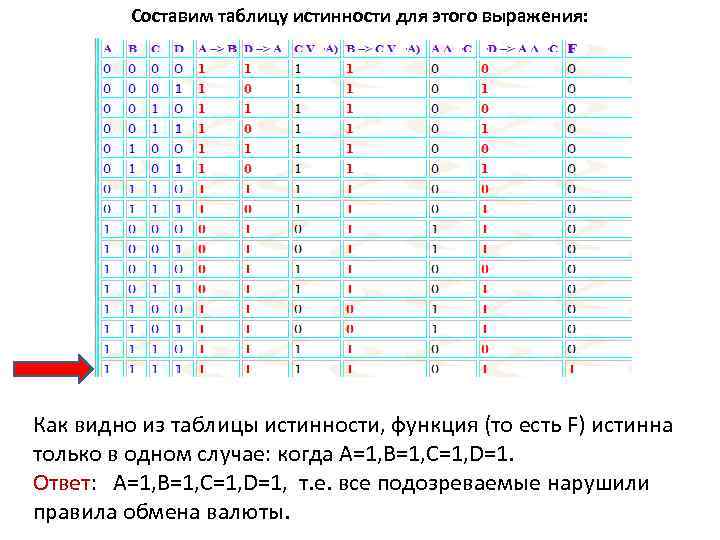
Составим таблицу истинности для этого выражения: Как видно из таблицы истинности, функция (то есть F) истинна только в одном случае: когда А=1, B=1, C=1, D=1. Ответ: А=1, B=1, C=1, D=1, т. е. все подозреваемые нарушили правила обмена валюты.

Следующие 2 задачи решите по аналогии.

Задача 2. • По обвинению в ограблении перед судом предстали Иванов, Петров, Сидоров. Следствием установлено следующее: 1) Если Иванов не виновен или Петров виновен, то Сидоров виновен. 2) Если Иванов не виновен, то Сидоров не виновен. • Виновен ли Иванов?

Задача 3. • Какие фирмы организуют выставки, если истинны два высказывания: «Фирма А организует выставку, а фирма С не организует» и «Если фирма В организует, то фирма С тоже организует» .

Равносильные логические выражения • Логические выражения, у которых последние столбцы таблиц истинности совпадают, называются равносильными. Для обозначения равносильных логических выражений используется знак «=» .

Пример 3. Докажем, что логические выражения А & B и А v В равносильны.
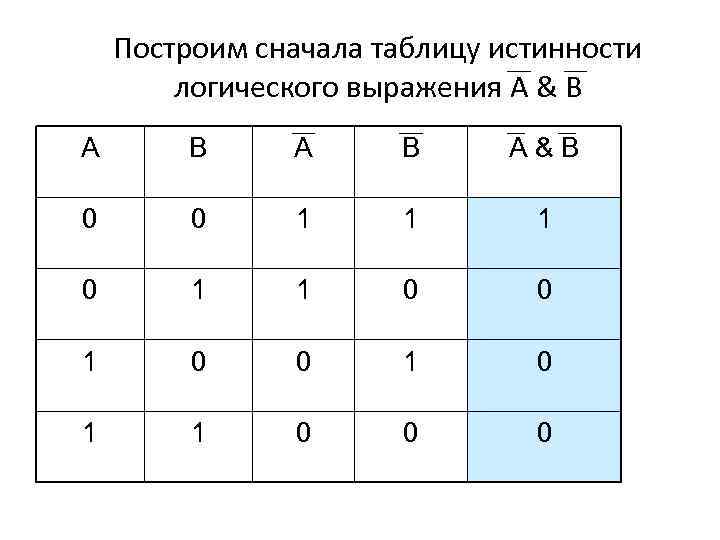
Построим сначала таблицу истинности логического выражения A & B A B A&B 0 0 1 1 1 0 0 1 0 1 1 0 0 0
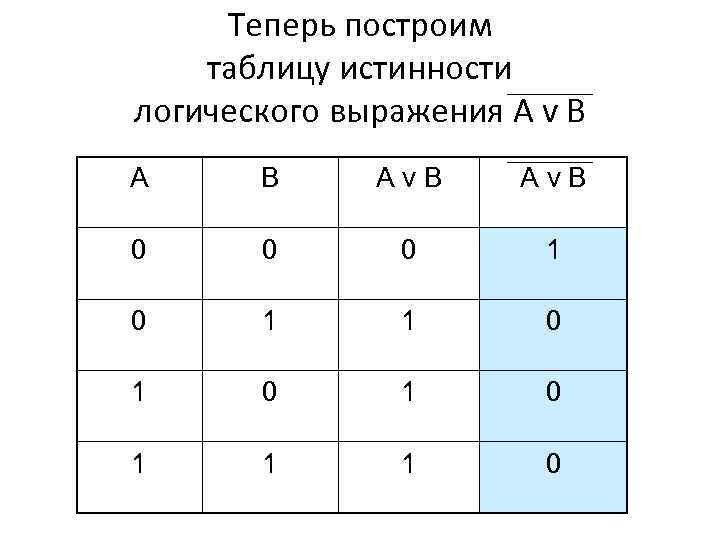
Теперь построим таблицу истинности логического выражения A v B Av. B 0 0 0 1 1 0 1 0 1 1 1 0
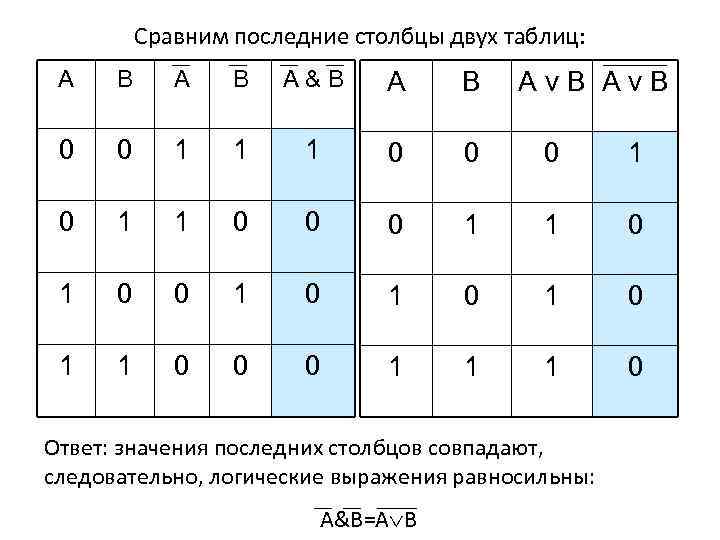
Сравним последние столбцы двух таблиц: A B A&B A B 0 0 1 1 1 0 0 0 1 1 0 0 1 0 1 1 0 0 0 1 1 1 0 Av. B Ответ: значения последних столбцов совпадают, следовательно, логические выражения равносильны: A&B=A B

Задача 4. • Доказать, используя таблицы истинности, что логические выражения A B и A&B равносильны.

Пример 4. Решение логических задач с помощью рассуждений Этим способом обычно решают несложные логические задачи. Задача: Вадим, Сергей и Михаил изучают различные иностранные языки: китайский, японский и арабский. На вопрос, какой язык изучает каждый из них, один ответил: "Вадим изучает китайский, Сергей не изучает китайский, а Михаил не изучает арабский". Впоследствии выяснилось, что в этом ответе только одно утверждение верно, а два других ложны. Какой язык изучает каждый из молодых людей? Решение. Имеется три утверждения: Вадим изучает китайский; Сергей не изучает китайский; Михаил не изучает арабский. Если верно первое утверждение, то верно и второе, так как юноши изучают разные языки. Это противоречит условию задачи, поэтому первое утверждение ложно. Если верно второе утверждение, то первое и третье должны быть ложны. При этом получается, что никто не изучает китайский. Это противоречит условию, поэтому второе утверждение тоже ложно. Остается считать верным третье утверждение, а первое и второе — ложными. Следовательно, Вадим не изучает китайский, китайский изучает Сергей. Ответ: Сергей изучает китайский язык, Михаил — японский, Вадим — арабский.

Задача 5. Один из 3 братьев поставил на скатерть кляксу. - Кто запачкал скатерть ? - спросила бабушка. - Витя не ставил кляксу, - сказал Алеша, - Это сделал Боря. - Ну а ты что скажешь? - спросила бабушка Борю. - Это Витя поставил кляксу, - сказал Боря, - а Алеша не пачкал скатерть. - Так я и знала, что вы друг на друга сваливать будете, - рассердилась бабушка. - Ну а каков твой ответ? - спросила она Витю. - Не сердись бабуля! Я знаю, что Боря не мог этого сделать. А я сегодня не готовил уроков. - сказал Витя. Оказалось, что двое мальчиков в каждом из двух своих заявлений сказали правду, а один оба раза сказал неправду. Кто поставил на скатерть кляксу?
контрольная работа по логике_14_мая.pptx