Тела вращения.Элементы тел вращения и формулы площади поверхности , объема.ppt
- Количество слайдов: 33
 Домашнее задание: • п. 125 -127 • № 1214 б, 1220 в, 1226 а, 1231 «Считай несчастным тот день и тот час, в который ты не усвоил ничего, и ничего не прибавил к своему образованию» Я. А. Коменский 2/1/2018 Логинова Н. В. МБОУ «СОШ № 16» 1
Домашнее задание: • п. 125 -127 • № 1214 б, 1220 в, 1226 а, 1231 «Считай несчастным тот день и тот час, в который ты не усвоил ничего, и ничего не прибавил к своему образованию» Я. А. Коменский 2/1/2018 Логинова Н. В. МБОУ «СОШ № 16» 1
 01. 02. 2018 Тела вращения Логинова Н. В. учитель математики МБОУ «СОШ № 16» г. Ижевска 9 класс 2
01. 02. 2018 Тела вращения Логинова Н. В. учитель математики МБОУ «СОШ № 16» г. Ижевска 9 класс 2
 ЦИЛИНДР: от греческого «валик, каток» Цилиндром называется тело, полученное при вращении прямоугольника вокруг оси, проходящей через одну из его сторон. 2/1/2018 Логинова Н. В. МБОУ «СОШ № 16» 3
ЦИЛИНДР: от греческого «валик, каток» Цилиндром называется тело, полученное при вращении прямоугольника вокруг оси, проходящей через одну из его сторон. 2/1/2018 Логинова Н. В. МБОУ «СОШ № 16» 3
 Основные определения Основаниями цилиндра называются круги, полученные в результате вращения сторон прямоугольника, смежных со стороной принадлежащей оси вращения. O 1 Н O Образующими цилиндра называются отрезки, соединяющие соответствующие точки окружностей кругов. R Радиусом цилиндра называется радиус его основания. Высотой цилиндра называется расстояние между плоскостями оснований. Осью цилиндра называется прямая, проходящая через центры оснований. 2/1/2018 Логинова Н. В. МБОУ «СОШ № 16» 4
Основные определения Основаниями цилиндра называются круги, полученные в результате вращения сторон прямоугольника, смежных со стороной принадлежащей оси вращения. O 1 Н O Образующими цилиндра называются отрезки, соединяющие соответствующие точки окружностей кругов. R Радиусом цилиндра называется радиус его основания. Высотой цилиндра называется расстояние между плоскостями оснований. Осью цилиндра называется прямая, проходящая через центры оснований. 2/1/2018 Логинова Н. В. МБОУ «СОШ № 16» 4
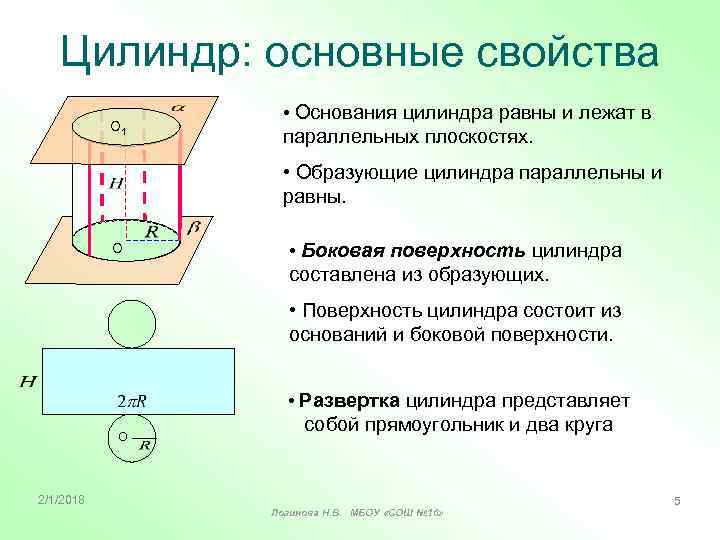 Цилиндр: основные свойства O 1 • Основания цилиндра равны и лежат в параллельных плоскостях. • Образующие цилиндра параллельны и равны. O • Боковая поверхность цилиндра составлена из образующих. • Поверхность цилиндра состоит из оснований и боковой поверхности. • Развертка цилиндра представляет O 2/1/2018 собой прямоугольник и два круга Логинова Н. В. МБОУ «СОШ № 16» 5
Цилиндр: основные свойства O 1 • Основания цилиндра равны и лежат в параллельных плоскостях. • Образующие цилиндра параллельны и равны. O • Боковая поверхность цилиндра составлена из образующих. • Поверхность цилиндра состоит из оснований и боковой поверхности. • Развертка цилиндра представляет O 2/1/2018 собой прямоугольник и два круга Логинова Н. В. МБОУ «СОШ № 16» 5
 Сечения цилиндра O 1 O 2/1/2018 Сечение цилиндра плоскостью, проходящей через ось цилиндра, называется осевым сечением. Сечение цилиндра плоскостью, перпендикулярной оси цилиндра, представляет собой круг, равный основанию. O 1 O Логинова Н. В. МБОУ «СОШ № 16» Сечение цилиндра плоскостью, параллельной оси цилиндра, представляет собой прямоугольник. Сечение цилиндра плоскостью, проходящей под углом к оси цилиндра, представляет собой эллипс. 6
Сечения цилиндра O 1 O 2/1/2018 Сечение цилиндра плоскостью, проходящей через ось цилиндра, называется осевым сечением. Сечение цилиндра плоскостью, перпендикулярной оси цилиндра, представляет собой круг, равный основанию. O 1 O Логинова Н. В. МБОУ «СОШ № 16» Сечение цилиндра плоскостью, параллельной оси цилиндра, представляет собой прямоугольник. Сечение цилиндра плоскостью, проходящей под углом к оси цилиндра, представляет собой эллипс. 6
 КОНУС: от греческого «сосновая шишка, остроконечная верхушка шлема» Конусом называется тело, полученное при вращении прямоугольного треугольника вокруг оси, содержащей его катет. 2/1/2018 Логинова Н. В. МБОУ «СОШ № 16» 7
КОНУС: от греческого «сосновая шишка, остроконечная верхушка шлема» Конусом называется тело, полученное при вращении прямоугольного треугольника вокруг оси, содержащей его катет. 2/1/2018 Логинова Н. В. МБОУ «СОШ № 16» 7
 Основные определения Основанием конуса называется круг, полученный в результате вращения катета, перпендикулярного стороне, принадлежащей оси вращения. Вершиной конуса называется точка, не А лежащая в плоскости этого круга. Радиусом конуса называется радиус его основания. Н О Образующими конуса называются отрезки, соединяющие вершину конуса с точками окружности основания. R В Высотой конуса называется перпендикуляр, опущенный из его вершины на плоскость основания. Осью прямого конуса называется прямая, содержащая его высоту. 2/1/2018 Логинова Н. В. МБОУ «СОШ № 16» 8
Основные определения Основанием конуса называется круг, полученный в результате вращения катета, перпендикулярного стороне, принадлежащей оси вращения. Вершиной конуса называется точка, не А лежащая в плоскости этого круга. Радиусом конуса называется радиус его основания. Н О Образующими конуса называются отрезки, соединяющие вершину конуса с точками окружности основания. R В Высотой конуса называется перпендикуляр, опущенный из его вершины на плоскость основания. Осью прямого конуса называется прямая, содержащая его высоту. 2/1/2018 Логинова Н. В. МБОУ «СОШ № 16» 8
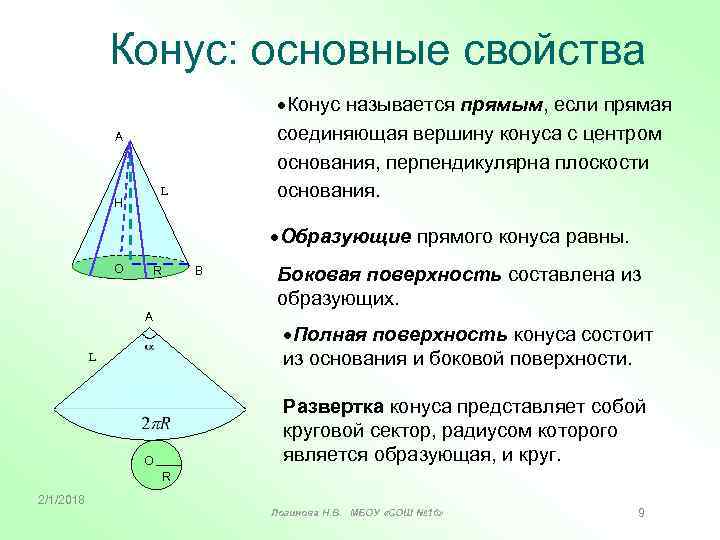 Конус: основные свойства Конус называется прямым, если прямая соединяющая вершину конуса с центром основания, перпендикулярна плоскости основания. А L Н Образующие прямого конуса равны. О R В А Боковая поверхность составлена из образующих. Полная поверхность конуса состоит из основания и боковой поверхности. L Развертка конуса представляет собой круговой сектор, радиусом которого является образующая, и круг. О R 2/1/2018 Логинова Н. В. МБОУ «СОШ № 16» 9
Конус: основные свойства Конус называется прямым, если прямая соединяющая вершину конуса с центром основания, перпендикулярна плоскости основания. А L Н Образующие прямого конуса равны. О R В А Боковая поверхность составлена из образующих. Полная поверхность конуса состоит из основания и боковой поверхности. L Развертка конуса представляет собой круговой сектор, радиусом которого является образующая, и круг. О R 2/1/2018 Логинова Н. В. МБОУ «СОШ № 16» 9
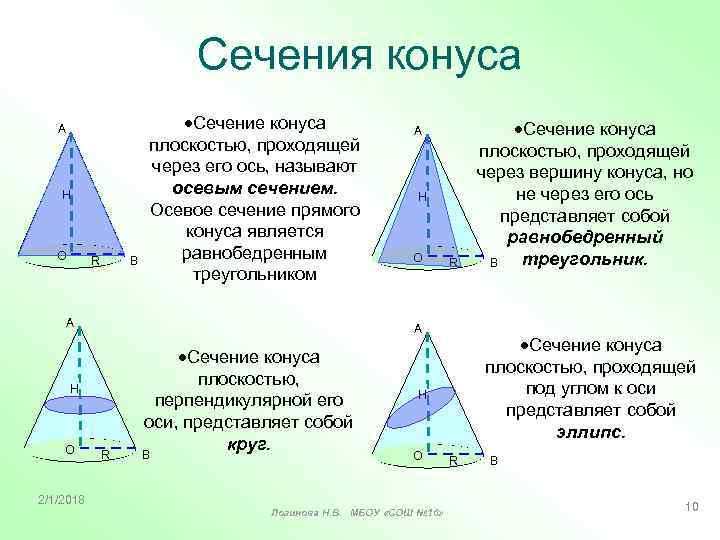 Сечения конуса А Н О R В Сечение конуса плоскостью, проходящей через его ось, называют осевым сечением. Осевое сечение прямого конуса является равнобедренным треугольником А 2/1/2018 Н О R А Н О А R Сечение конуса плоскостью, перпендикулярной его оси, представляет собой круг. В Сечение конуса плоскостью, проходящей под углом к оси представляет собой эллипс. Н О Логинова Н. В. МБОУ «СОШ № 16» Сечение конуса плоскостью, проходящей через вершину конуса, но не через его ось представляет собой равнобедренный треугольник. В R В 10
Сечения конуса А Н О R В Сечение конуса плоскостью, проходящей через его ось, называют осевым сечением. Осевое сечение прямого конуса является равнобедренным треугольником А 2/1/2018 Н О R А Н О А R Сечение конуса плоскостью, перпендикулярной его оси, представляет собой круг. В Сечение конуса плоскостью, проходящей под углом к оси представляет собой эллипс. Н О Логинова Н. В. МБОУ «СОШ № 16» Сечение конуса плоскостью, проходящей через вершину конуса, но не через его ось представляет собой равнобедренный треугольник. В R В 10
 Усеченный конус Усеченным конусом называется часть конуса, заключенная между его основанием и секущей плоскостью, параллельной плоскости основания конуса. 2/1/2018 Логинова Н. В. МБОУ «СОШ № 16» 11
Усеченный конус Усеченным конусом называется часть конуса, заключенная между его основанием и секущей плоскостью, параллельной плоскости основания конуса. 2/1/2018 Логинова Н. В. МБОУ «СОШ № 16» 11
 Основные определения Основаниями усеченного конуса называются r основание данного конуса и круг, полученный в L Н R сечении этого конуса плоскостью. Образующими называются отрезки образующих конической поверхности, расположенные между основаниями усеченного конуса. Радиусами усеченного конуса называются радиусы его оснований. Высотой называется отрезок, соединяющий центры оснований усеченного конуса. 2/1/2018 Логинова Н. В. МБОУ «СОШ № 16» 12
Основные определения Основаниями усеченного конуса называются r основание данного конуса и круг, полученный в L Н R сечении этого конуса плоскостью. Образующими называются отрезки образующих конической поверхности, расположенные между основаниями усеченного конуса. Радиусами усеченного конуса называются радиусы его оснований. Высотой называется отрезок, соединяющий центры оснований усеченного конуса. 2/1/2018 Логинова Н. В. МБОУ «СОШ № 16» 12
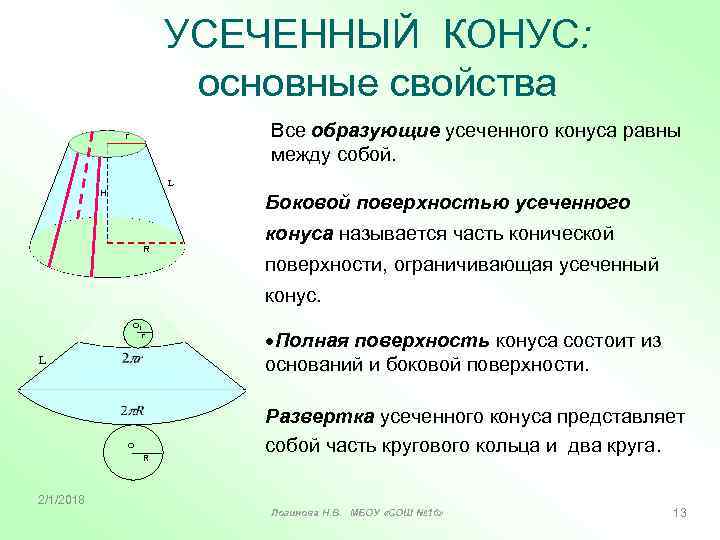 УСЕЧЕННЫЙ КОНУС: основные свойства Все образующие усеченного конуса равны между собой. r L Н Боковой поверхностью усеченного конуса называется часть конической R поверхности, ограничивающая усеченный конус. О 1 r L О R 2/1/2018 Полная поверхность конуса состоит из оснований и боковой поверхности. Развертка усеченного конуса представляет собой часть кругового кольца и два круга. Логинова Н. В. МБОУ «СОШ № 16» 13
УСЕЧЕННЫЙ КОНУС: основные свойства Все образующие усеченного конуса равны между собой. r L Н Боковой поверхностью усеченного конуса называется часть конической R поверхности, ограничивающая усеченный конус. О 1 r L О R 2/1/2018 Полная поверхность конуса состоит из оснований и боковой поверхности. Развертка усеченного конуса представляет собой часть кругового кольца и два круга. Логинова Н. В. МБОУ «СОШ № 16» 13
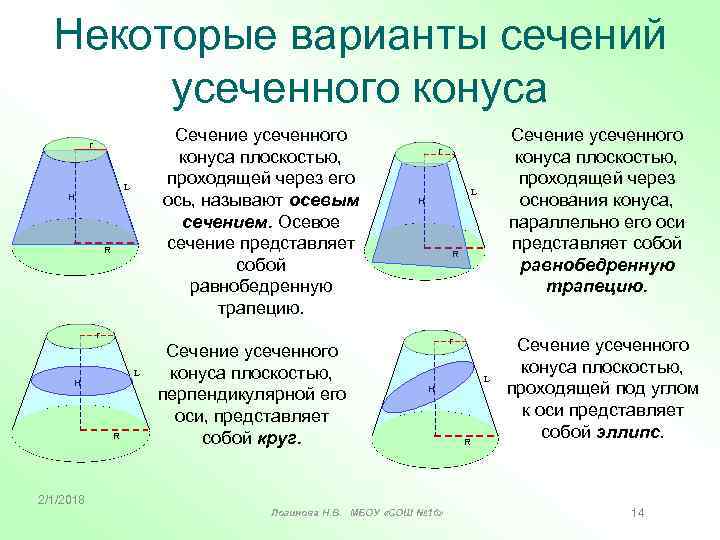 Некоторые варианты сечений усеченного конуса Сечение усеченного конуса плоскостью, проходящей через его ось, называют осевым сечением. Осевое сечение представляет собой равнобедренную трапецию. r L Н R 2/1/2018 Сечение усеченного конуса плоскостью, перпендикулярной его оси, представляет собой круг. Сечение усеченного конуса плоскостью, проходящей через основания конуса, параллельно его оси представляет собой равнобедренную трапецию. r r L Н Логинова Н. В. МБОУ «СОШ № 16» R Сечение усеченного конуса плоскостью, проходящей под углом к оси представляет собой эллипс. 14
Некоторые варианты сечений усеченного конуса Сечение усеченного конуса плоскостью, проходящей через его ось, называют осевым сечением. Осевое сечение представляет собой равнобедренную трапецию. r L Н R 2/1/2018 Сечение усеченного конуса плоскостью, перпендикулярной его оси, представляет собой круг. Сечение усеченного конуса плоскостью, проходящей через основания конуса, параллельно его оси представляет собой равнобедренную трапецию. r r L Н Логинова Н. В. МБОУ «СОШ № 16» R Сечение усеченного конуса плоскостью, проходящей под углом к оси представляет собой эллипс. 14
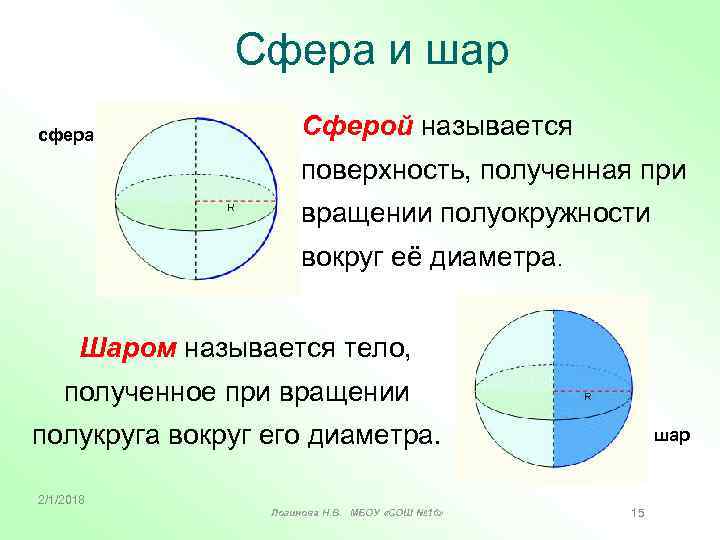 Сфера и шар сфера Сферой называется поверхность, полученная при вращении полуокружности вокруг её диаметра. Шаром называется тело, полученное при вращении полукруга вокруг его диаметра. 2/1/2018 Логинова Н. В. МБОУ «СОШ № 16» шар 15
Сфера и шар сфера Сферой называется поверхность, полученная при вращении полуокружности вокруг её диаметра. Шаром называется тело, полученное при вращении полукруга вокруг его диаметра. 2/1/2018 Логинова Н. В. МБОУ «СОШ № 16» шар 15
 Основные определения Шаром называется тело, которое состоит из всех точек пространства, находящихся на расстоянии, не большем данного, от данной точки. D R Эта точка называется центром шара, а данное расстояние называется радиусом шара. O R R R Граница шара называется шаровой поверхностью или сферой. Любой отрезок, соединяющий центр шара с точкой шаровой поверхности, называется радиусом. Отрезок, соединяющий две точки шаровой поверхности и проходящий через центр шара, называется диаметром. 2/1/2018 Логинова Н. В. МБОУ «СОШ № 16» 16
Основные определения Шаром называется тело, которое состоит из всех точек пространства, находящихся на расстоянии, не большем данного, от данной точки. D R Эта точка называется центром шара, а данное расстояние называется радиусом шара. O R R R Граница шара называется шаровой поверхностью или сферой. Любой отрезок, соединяющий центр шара с точкой шаровой поверхности, называется радиусом. Отрезок, соединяющий две точки шаровой поверхности и проходящий через центр шара, называется диаметром. 2/1/2018 Логинова Н. В. МБОУ «СОШ № 16» 16
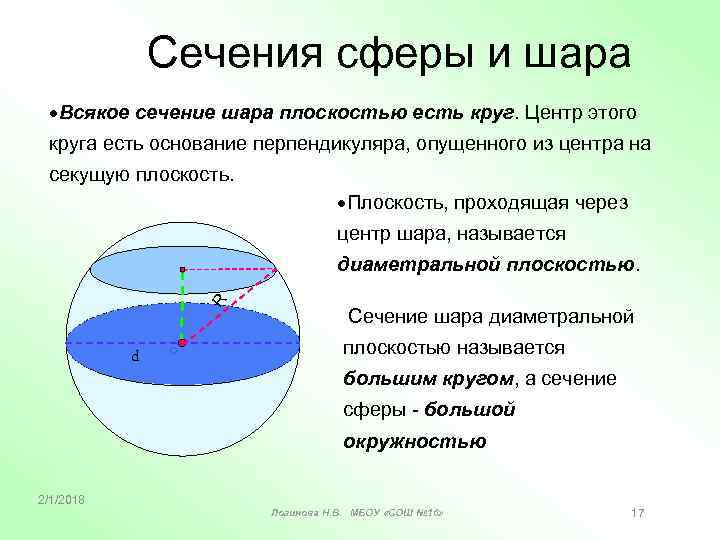 Сечения сферы и шара Всякое сечение шара плоскостью есть круг. Центр этого круга есть основание перпендикуляра, опущенного из центра на секущую плоскость. Плоскость, проходящая через центр шара, называется R диаметральной плоскостью. R d Сечение шара диаметральной плоскостью называется O большим кругом, а сечение R сферы - большой окружностью 2/1/2018 Логинова Н. В. МБОУ «СОШ № 16» 17
Сечения сферы и шара Всякое сечение шара плоскостью есть круг. Центр этого круга есть основание перпендикуляра, опущенного из центра на секущую плоскость. Плоскость, проходящая через центр шара, называется R диаметральной плоскостью. R d Сечение шара диаметральной плоскостью называется O большим кругом, а сечение R сферы - большой окружностью 2/1/2018 Логинова Н. В. МБОУ «СОШ № 16» 17
 Формулы площади поверхности и объема тел вращения Название тела Формула площади бок. площади полной поверхности Формула объема Цилиндр Конус Усеченный конус Шар Логинова Н. В. МБОУ «СОШ № 16» 2/1/2018 18
Формулы площади поверхности и объема тел вращения Название тела Формула площади бок. площади полной поверхности Формула объема Цилиндр Конус Усеченный конус Шар Логинова Н. В. МБОУ «СОШ № 16» 2/1/2018 18
 Задачи С ПРАКТИЧЕСКИМ СОДЕРЖАНИЕМ 2/1/2018 Логинова Н. В. МБОУ «СОШ № 16» 19
Задачи С ПРАКТИЧЕСКИМ СОДЕРЖАНИЕМ 2/1/2018 Логинова Н. В. МБОУ «СОШ № 16» 19
 Задача 1. Токарю надо выточить деталь в форме цилиндра высотой 5 см и объёмом около 140 см 3. Как это сделать? Показать решение 2/1/2018 Логинова Н. В. МБОУ «СОШ № 16» 20
Задача 1. Токарю надо выточить деталь в форме цилиндра высотой 5 см и объёмом около 140 см 3. Как это сделать? Показать решение 2/1/2018 Логинова Н. В. МБОУ «СОШ № 16» 20
 Задача 1. Токарю надо выточить деталь в форме цилиндра высотой 5 см и объёмом около 140 см 3. Как это сделать? Дано: цилиндр, V=140 см 3 , h =5 см Найти: R Решение 2/1/2018 Логинова Н. В. МБОУ «СОШ № 16» 21
Задача 1. Токарю надо выточить деталь в форме цилиндра высотой 5 см и объёмом около 140 см 3. Как это сделать? Дано: цилиндр, V=140 см 3 , h =5 см Найти: R Решение 2/1/2018 Логинова Н. В. МБОУ «СОШ № 16» 21
 Задача 2. Ведро имеет форму усеченного конуса, радиусы оснований которого равны 15 см и 10 см, а образующая равна 30 см. Сколько килограммов краски нужно взять для того, чтобы покрасить с обеих сторон 100 таких ведер, если на 1 квадратный метр требуется 150 г краски? R 2/1/2018 Логинова Н. В. МБОУ «СОШ № 16» 22
Задача 2. Ведро имеет форму усеченного конуса, радиусы оснований которого равны 15 см и 10 см, а образующая равна 30 см. Сколько килограммов краски нужно взять для того, чтобы покрасить с обеих сторон 100 таких ведер, если на 1 квадратный метр требуется 150 г краски? R 2/1/2018 Логинова Н. В. МБОУ «СОШ № 16» 22
 Решите задачи: № 1229 2/1/2018 № 1217 Логинова Н. В. МБОУ «СОШ № 16» № 1228 23
Решите задачи: № 1229 2/1/2018 № 1217 Логинова Н. В. МБОУ «СОШ № 16» № 1228 23
 Задача № 1229. Сколько кожи пойдет на покрытие футбольного мяча радиуса 10 см (на швы добавить 8% от площади поверхности мяча)? O 2/1/2018 R Логинова Н. В. МБОУ «СОШ № 16» 24
Задача № 1229. Сколько кожи пойдет на покрытие футбольного мяча радиуса 10 см (на швы добавить 8% от площади поверхности мяча)? O 2/1/2018 R Логинова Н. В. МБОУ «СОШ № 16» 24
 Задача № 1217. Сколько квадратных метров листовой жести пойдет на изготовление трубы длиной 4 м и диаметром 20 см, если на швы необходимо добавить 2, 5% от площади её боковой поверхности? 2/1/2018 Логинова Н. В. МБОУ «СОШ № 16» 25
Задача № 1217. Сколько квадратных метров листовой жести пойдет на изготовление трубы длиной 4 м и диаметром 20 см, если на швы необходимо добавить 2, 5% от площади её боковой поверхности? 2/1/2018 Логинова Н. В. МБОУ «СОШ № 16» 25
 Задача № 1228. Стаканчик для мороженого конической формы имеет глубину 12 см и диаметр верхней части 5 см. На него сверху положили две ложки мороженого в виде полушарий диаметром 5 см. Переполнит ли мороженое стаканчик, если оно растает? Ответ: нет 2/1/2018 Логинова Н. В. МБОУ «СОШ № 16» 26
Задача № 1228. Стаканчик для мороженого конической формы имеет глубину 12 см и диаметр верхней части 5 см. На него сверху положили две ложки мороженого в виде полушарий диаметром 5 см. Переполнит ли мороженое стаканчик, если оно растает? Ответ: нет 2/1/2018 Логинова Н. В. МБОУ «СОШ № 16» 26
 Повторим ещё раз формулы • • • Цилиндр Конус Усеченный конус Шар и сфера Формулы площади поверхности и объема тел вращения 2/1/2018 Логинова Н. В. МБОУ «СОШ № 16» 27
Повторим ещё раз формулы • • • Цилиндр Конус Усеченный конус Шар и сфера Формулы площади поверхности и объема тел вращения 2/1/2018 Логинова Н. В. МБОУ «СОШ № 16» 27
 Цилиндр: R - радиус основания; H - высота Площадь полной поверхности: Площадь боковой поверхности: O 1 H O Площадь основания: R Объем цилиндра: O 2/1/2018 Логинова Н. В. МБОУ «СОШ № 16» 28
Цилиндр: R - радиус основания; H - высота Площадь полной поверхности: Площадь боковой поверхности: O 1 H O Площадь основания: R Объем цилиндра: O 2/1/2018 Логинова Н. В. МБОУ «СОШ № 16» 28
 КОНУС: R - радиус основания; Н – высота; L - образующая Площадь полной поверхности: А Площадь боковой поверхности: L Н Площадь основания: О R В Объем конуса: 2/1/2018 Логинова Н. В. МБОУ «СОШ № 16» 29
КОНУС: R - радиус основания; Н – высота; L - образующая Площадь полной поверхности: А Площадь боковой поверхности: L Н Площадь основания: О R В Объем конуса: 2/1/2018 Логинова Н. В. МБОУ «СОШ № 16» 29
 УСЕЧЕННЫЙ КОНУС: R и r - радиусы оснований; Н – высота; L - образующая Площадь полной поверхности: Площадь боковой поверхности: r L Н R 2/1/2018 Площадь оснований: Объем усеченного конуса: Логинова Н. В. МБОУ «СОШ № 16» 30
УСЕЧЕННЫЙ КОНУС: R и r - радиусы оснований; Н – высота; L - образующая Площадь полной поверхности: Площадь боковой поверхности: r L Н R 2/1/2018 Площадь оснований: Объем усеченного конуса: Логинова Н. В. МБОУ «СОШ № 16» 30
 СФЕРА И ШАР: R - сферы; d - диаметр R Площадь поверхности сферы: d Объем шара: O R R R 2/1/2018 Логинова Н. В. МБОУ «СОШ № 16» 31
СФЕРА И ШАР: R - сферы; d - диаметр R Площадь поверхности сферы: d Объем шара: O R R R 2/1/2018 Логинова Н. В. МБОУ «СОШ № 16» 31
 Формулы площади поверхности и объема тел вращения Название тела Формула площади бок. площади полной поверхности Формула объема Цилиндр Конус Усеченный конус Шар Логинова Н. В. МБОУ «СОШ № 16» 2/1/2018 32
Формулы площади поверхности и объема тел вращения Название тела Формула площади бок. площади полной поверхности Формула объема Цилиндр Конус Усеченный конус Шар Логинова Н. В. МБОУ «СОШ № 16» 2/1/2018 32
 Спасибо за внимание! 2/1/2018 Логинова Н. В. МБОУ «СОШ № 16» 33
Спасибо за внимание! 2/1/2018 Логинова Н. В. МБОУ «СОШ № 16» 33


