Doing Mathematics as a Vehicle for Developing Secondary

Doing Mathematics as a Vehicle for Developing Secondary Preservice Math Teachers’ Knowledge of Mathematics for Teaching Gail Burrill Michigan State University Burrill@msu. edu

How much do all 3 chickens weigh? Each chicken? Kindt et al, 2006

Pedagogical Content Knowledge Lee Shulman, 1986, pp. 9 -10 For the most regularly taught topics in one’s subject area: • The most useful representations of ideas • The most powerful analogies, illustrations, examples an demonstrations • Ways of representing and formulating the subject that make it comprehensible to others • A veritable armamentarium of alternative forms of representation • Understanding of why certain concepts are easy or difficult to learn

Mathematical Knowledge for Teaching Deborah Ball & Hyman Bass, 2000 • “a kind of understanding. . not something a mathematician would have, but neither would be part of a high school social studies’ teacher’s knowledge” • “teaching is a form of mathematical work… involves a steady stream of mathematical problems that teachers must solve” • Features include: unpacked knowledge, connectedness across mathematical domains and over time (seeing mathematical horizons)

Mathematical Knowledge for teaching • Trimming- making mathematics available yet retaining mathematical integrity • Unpacking-making the math explicit • Making connections visible- within and across mathematical domains • Using visualization to scaffold learning • Considering curricular trajectories • Flexibly moving among strategies/ approaches adapted from Ferrini-Mundy et al, 2004

Secondary Preservice Program at MSU Three precursor general ed courses Year-long methods course (4 hours a week) as a senior blended with 4 hours per week in the field and 2 hours a week of teaching lab, special ed and minor Mathematics Majors Post graduate fifth year-long internship program General secondary program goals- no specific guidelines for math

Methods Course First semester: - Observing teaching - Curriculum - Designing lessons Second semester: - Equity - Assessment - Designing lessons

Goals Course Goals • Deepen and connect mathematical content knowledge with student mathematical understanding. • Analyze from a new perspective what mathematics is and what it means to learn, do and teach mathematics. • Learn to listen to and look at students’ work as a way to inform teaching, using evidence from these to make decisions. Adapted from Roneau & Taylor, 2007

Course Goals • Learn to design and implement lessons to engage students in learning (tasks, sequence, discourse, questioning, use of technology) • Learn to reflect on practice – both from a perspective as a teacher, a researcher, a learner, and from the perspective of what you see students learning • Recognize what is meant by equity and access to quality mathematics for students, parents and communities (including attention to policy) Adapted from Roneau & Taylor, 2007

Weekly math problems Quarterly problem sets • Algebra • Geometry • Number • Data and statistics Chosen to reflect the scope and depth of the area Assigned as homework, discussion managed by a pair of randomly assigned students who meet with instructors to discuss problem, solutions and misconceptions

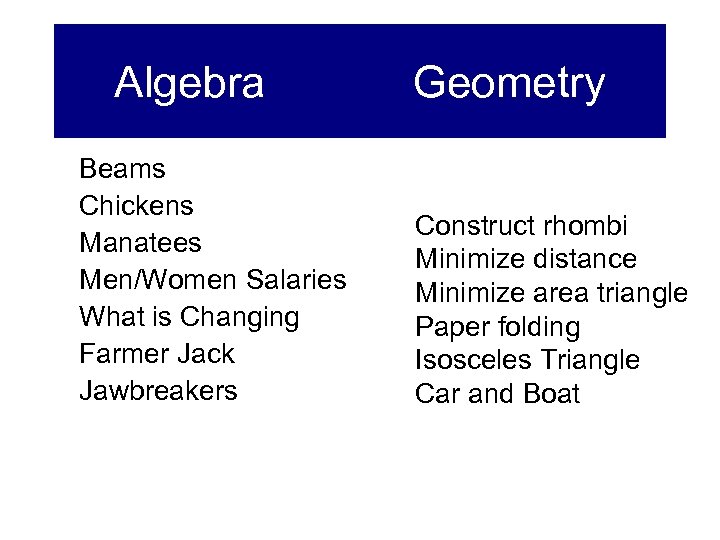Algebra Beams Chickens Manatees Men/Women Salaries What is Changing Farmer Jack Jawbreakers Geometry Construct rhombi Minimize distance Minimize area triangle Paper folding Isosceles Triangle Car and Boat

Problem characteristics Accessible by different approaches at the same level Accessible by different mathematical approaches Surface mathematical connections Usually involve a connection between symbols and some other representation Provide opportunities to surface misconceptions Lend themselves to exploiting different ways to manage student mathematical discussions Different types or nature of problems

“Different” tasks Sum is more than the parts - confidence interval Multiple interpretations that lead to thinking hard about the mathematics Patterns emerge across different problems - simulations Make concept explicit -construct rhombi Constructing own problems -What is changing?

Different mathematical approaches

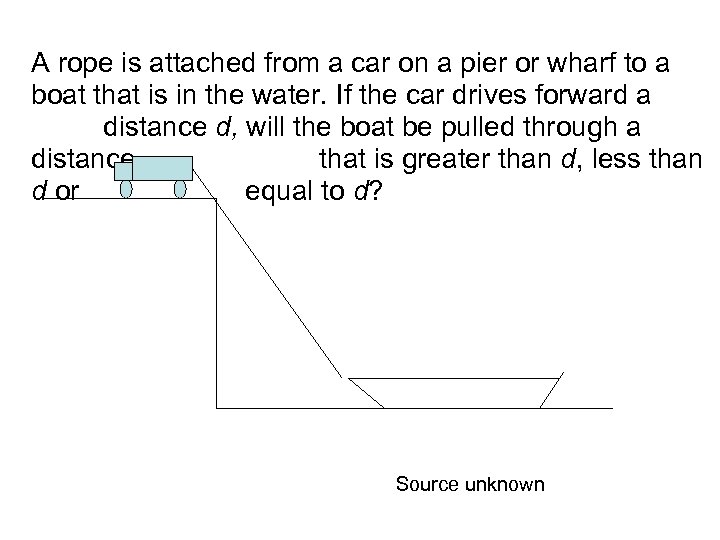A rope is attached from a car on a pier or wharf to a boat that is in the water. If the car drives forward a distance d, will the boat be pulled through a distance that is greater than d, less than d or equal to d? Source unknown

Strategies Calculus Trigonometry Pythagorean Theorem Coordinate geometry Triangle theorems

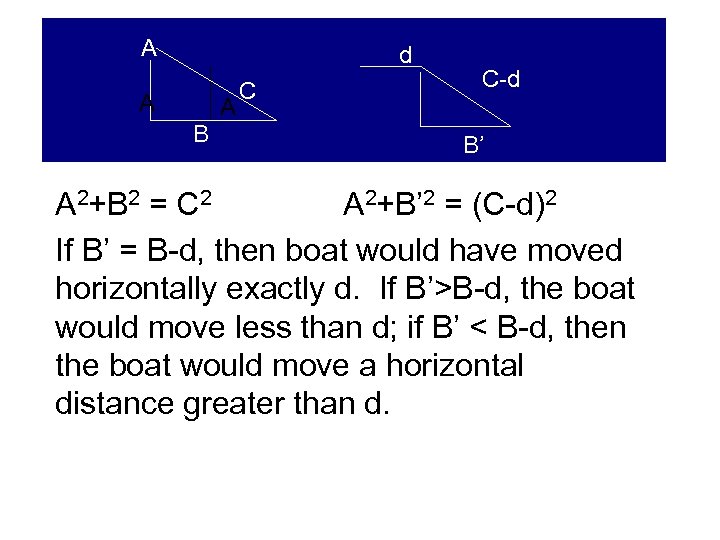A d A A B C C-d B’ A 2+B 2 = C 2 A 2+B’ 2 = (C-d)2 If B’ = B-d, then boat would have moved horizontally exactly d. If B’>B-d, the boat would move less than d; if B’ < B-d, then the boat would move a horizontal distance greater than d.

Surface mathematical connections

Making connections • How many handshakes are possible between 2 people? What about 3, 4, 5, 6, and 7 people? Try to come up with an equation for n number of people. Make a list or table of the number of possible handshakes for each amount of people. Do you know what these numbers are?

Making connections – Study the table of Pythagorean triples. – Make a conjecture about all of the Pythagorean triples that have two consecutive integers as a leg and the hypotenuse that is not true for all Pythagorean triples.

Making connections • Suppose you have a bag with two different colors of chips in it, red and blue. If you draw two chips from the bag without replacement, how many of each color chip do you need to have in the bag in order for the probability of getting two chips of the same color to equal the probability of getting two chips, one of each color.

Making connections Find the pattern if the sequence continues. Find an equation for the number of dots in the nth figure. Make a list of the number of dots for the first 6 figures. Do you know what these numbers are? ∙ ∙ ∙ Figure 1 ∙ ∙ ∙ Figure 2 ∙ ∙ ∙ Figure 3 ∙

Manage discussions

Isosceles Triangle Given the isosceles triangle ABC where AB = BC = 12. AC is 13. BD is the altitude to AC, and D is on AC. AE is the altitude to BC, and E is on BC. Find DE

Isosceles Triangle • “… students check the papers of their peers. … a great way to increase the understanding. Three indicators of understanding: communicate a concept to another person, reflect on a concept meaningfully, or apply a concept to a new situation, … When a student is asking questions of the original paper owner the two are communicating about math, conveying some understanding. The grader is reflecting about the method the first student used to solve the problem and the original student reflects about the comments and questions posed by the grader. If the methods of solving are different they have to look in detail at how someone else did the problem. ” Preservice student

Student designed problems

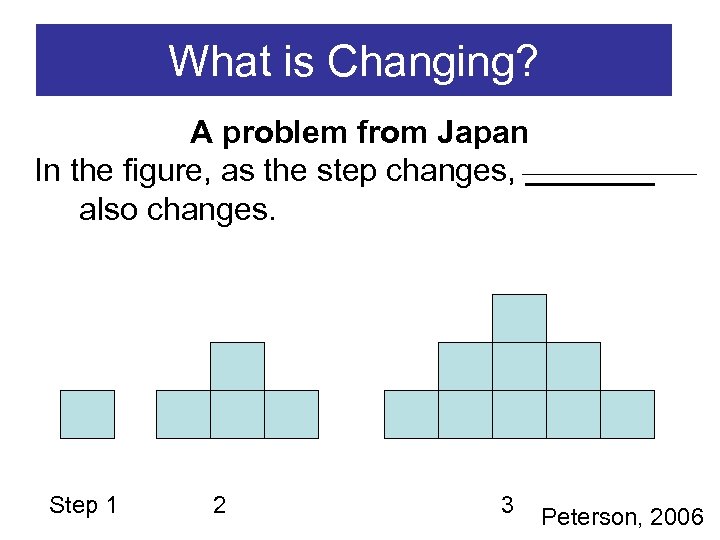What is Changing? A problem from Japan In the figure, as the step changes, also changes. Step 1 2 3 Peterson, 2006

What is changing? • • • Area Perimeter Length of longest side Number of intersections Number of right angles Sum of interior angles Number of parallel line segments Number of squares ….

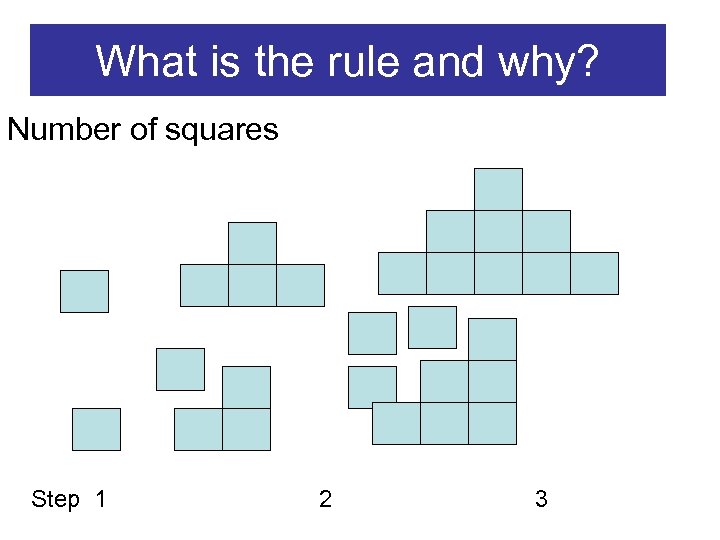What is the rule and why? Number of squares Step 1 2 3

Instruction: Managing solutions

Patterns/Reasoning & Proof • What constitutes valid justification? • Lack of connection to a geometric scheme that established a relation between the rule and the context. • Focus on particular values rather than making generalizations • Inability to generalize across contexts (Lanin, 2005) • Algebraic notation often confusing and not used (Zazskis & Liljedah, 2002)

Farmer Jack • Farmer Jack harvested 30, 000 bushels of corn over a ten-year period. He wanted to make a table showing that he was a good farmer and that his harvest had increased by the same amount each year. Create Farmer Jack’s table for the ten year period. (Burrill, 2004)

Burrill, 2004

Using Variables year 1 x 2 x+x 3 x+x+x 4 4 x 5 5 x 6 6 x 7 7 x 8 8 x 9 9 x 10 Burrill, 2004 Bushes per year 10 x Total

Burrill, 2004

Burrill, 2004

“Let d be the yearly increase and an be the amount harvested in year n. Then an+1 = an+d an = a 1 + (n-1)d. The condition is that the 10 year total harvest is 30000 bushels, thus, S 10 = ∑an = 30000 where S 10 is the total number of bushels after 10 years. Now, Sn = (n/2)(a 1+an), so S 10 = (10/2)(a 1+a 10) = 5(a 1 + a 1+ 9 d) = 30000. So 2 a 1+9 d = 6000. Any pair (a, d) where a and d are both greater than 0 will produce a suitable. There an infinite number of tables if you do not restrict the values to be positive integers. ” Burrill, 2004

Research on Functions Teaching issues • Students accept different answers to same problem rather than reject a procedure they feel is correct or explore why the difference (Sfard &Linchveski, 1994) • Form has consequences for learning (y = mx + b vs y = b + x(m); point slope form-y=y 1+ m(x-x 1) (Confrey & Smith, 1994)

A disconnect that needs explaining

Knowledge for Teaching • Unpacking the mathematical story • Making connections • Curricular knowledge • Making assumptions explicit

Knowledge for teaching?

Misconceptions • “They chose solutions that built off of one another, and the first solution was actually a misconception and the last was a general solution to the problem. JJ presented his misconception first and admitted that he “did it wrong. ” He went through his thought process and then explained how he figured out it was a misconception. After the solutions had been presented the class talked about how the misconception helps other students who also had this misconception feel justified that it wasn’t just them who had the mistake. Before this course I couldn’t think of why you would want to show a misconception to the class, but I now understand that talking about a misconception can be used to help students understand. If a student can explain what they have done wrong in a problem, it means that they have learned something. ”

Managing discussions • “As the students were writing up their solutions, the rest of the class was supposed to figure out the different solutions presented. This was discussed in class as a way to keep all the students engaged in the lesson. Watching the video, it seems this might not be the best way to keep students engaged because most of the class was no longer looking at the solutions; instead they were having side conversations with one another”. Preservice student

Defending thinking- evidence of understanding • …students were asked to do a think, pair, share discussion. The students thought individually about the problem as homework, came to class with their completed proofs, paired off and each pair discussed how they did the problem. The pairs picked one proof to put up on the board, and students walked around the room and took notes about the other proofs. • After the gallery walk the students were brought back together, and asked questions about what they didn’t get directly to the pair who wrote the proof. The teacher asked questions of them, too. ” Preservice Student

“habits of mind” Need for precision Vocabulary expression/equation construct/draw “lines are similar” Trimming division never makes bigger a 1 in recursive definitions

“habits of mind” The nature and role of proof: mix converse/statement assume what proving prove by example prove by pattern Definitions Assumptions and their consequences

“habits of mind” Doing math is a way of thinking More than routine procedures Problems out of context of unit Takes time Errors can be productive

“habits of mind” Not all math is equal underlying concepts should drive instruction Not all solutions are equal

“habits of mind” Math makes sense Chickens Ratio problem Farmer Jack

Making connections Solve each problem using at least two different approaches students might use. 1. Which is the best buy for barbecue sauce: 18 oz at 79 cents or 14 oz at 81 cents? NRC, 2001

Polya’s Ten Commandments Read faces of students Give students “know how”, attitudes of mind, habit of methodical work Let students guess before you tell them Suggest it; do not force it down their throats (Polya, 1965, p. 116)

Polya’s Ten Commandments Be interested in the subject Know about ways of learning Let students learn guessing Let students learn proving Look at features of problems that suggest solution methods (Polya, 1965, p. 116)

References • Roneau, R. & Taylor, T. (2007). Presession working grouop at Association of Mathematics Teacher Educators Annual meeting. • Ball, D. L. & Bass, H. (2000). Interweaving content and pedagogy in teaching and learning to teach: Knowing and using mathematics. In J. • Burrill, G. (2004). “Mathematical Tasks that Promote Thinking and Reasoning: The Case of Farmer Jack” in Mathematik lehren • Confery, J. & Smith, E. (1994). Exponential functions, rates of change, and the multiplicative unit. Educational Studies in Mathematics. 26: 135164. • Ferrini-Mundy, J. , Floden, R. , Mc. Crory, Burrill, G. , & Sandhow, D. (2004). Knowledge for teaching school algebra: challenges in developing in analytic framework. unpublished paper • Kazemi, E. & Franke, Megan L. (2004). Teacher learning in mathematics: using student work to promote collective inquiry. Journal of Mathematics Teacher Education, 7, 203 -235.

• Kindt, M. , Abels, M. , Meyer, M. , Pligge, M. (2006). Comparing Quantities. In Wisconsin Center for Education Research & Freudenthal Institute (Eds. ), Mathematics in context. Chicago: Encyclopedia Britannica • Lannin, John K. (2005). Generalization and justification: the challenge of introducing algebraic reasoning through patterning activities. Mathematical Thinking and Learning, 73(7), 231 -258. • National Research Council. (1999). How People Learn: Bain, mind, experience, and school. Bransford, J. D. , Brown, A. L. , & Cocking, R. R. (Eds. ). Washington, DC: National Academy Press. • Polya, G. (1965). Mathematical discovery: On understanding, learning, and teaching problem solving. • Peterson, B. (2006) Linear and Quadratic Change: A problem from Japan. The Mathematics Teacher, Vol 100, No. 3. PP. 206 -212. • Sfard, A. , & Linchevski, L. (1994). Between Arithmetic and Algebra: In the search of a missing link. The case of equations and inequalities. Rendicondi del Seminario Matematico, 52 (3), 279 -307.

• Shulman, L. S. (1986). Those who understand: Knowledge growth in teaching. Educational Researcher. 15 (2): 4 - 14. • Zazkis, R. & Liljedahl, P. (2002). Generalization of patterns: the tension between algebraic thinking and algebraic notation. Educational Studies in Mathematics 49, 379 – 402.