Doctoral Defence Characterization Modelling and Control of Mechanical

Doctoral Defence Characterization, Modelling and Control of Mechanical Systems Comprising Material and Geometrical Nonlinearities Tegoeh Tjahjowidodo Katholieke Universiteit Leuven Departement Werktuigkunde, Div. PMA Thursday 16 November 2006 Tegoeh Tjahjowidodo

Overview Introduction Geometric Nonlinearity Material Nonlinearity Control of Nonlinear Systems Application on Real System Conclusions Introduction – Nonlinearity sources – Dynamic signal classification Geometric Nonlinearity (Backlash) Material Nonlinearity (Friction) Control of Nonlinear Systems Application on a Real System Mechanical Systems with Harmonic Drive elements Conclusions Tegoeh Tjahjowidodo

Introduction Geometric Nonlinearity Material Nonlinearity Control of Nonlinear Systems Motivation: Having better understanding of a system via appropriate techniques System Identification ! Application on Real System Conclusions Identification purposes: There is no general identification method applicable – Dynamic behaviour analysis to all systems. – Design engineering – Damage detection this– Control design characteristic of the system and depends on the type of the signal involved in the identification. Tegoeh Tjahjowidodo

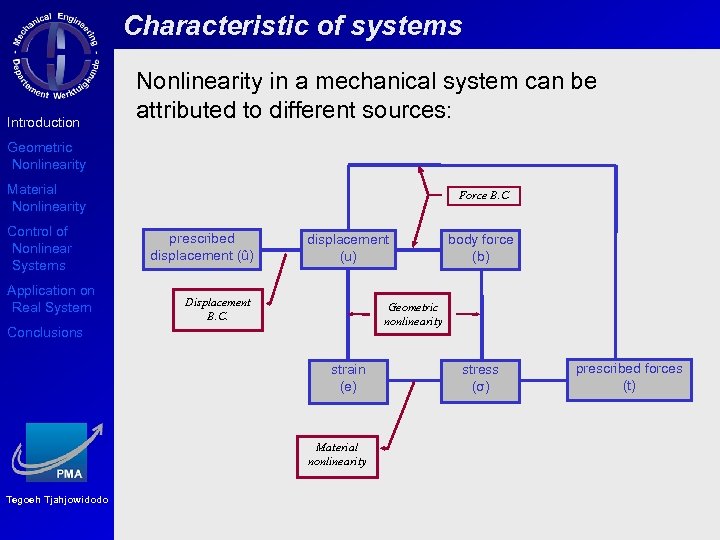Characteristic of systems Introduction Nonlinearity in a mechanical system can be attributed to different sources: Geometric Nonlinearity Material Nonlinearity Control of Nonlinear Systems Application on Real System Force B. C prescribed displacement (û) displacement (u) Displacement B. C. Geometric nonlinearity Conclusions strain (e) Material nonlinearity Tegoeh Tjahjowidodo body force (b) stress (σ) prescribed forces (t)

Geometrical and Material Nonlinearities Geometric Nonlinearity Introduction Geometric Nonlinearity Material Nonlinearity Control of Nonlinear Systems Application on Real System Conclusions – the change in geometry as the structure deforms causes a nonlinear change of the parameters in the system hardening spring, softening spring, saturation, … Material Nonlinearity – the behaviour of material depends on the current deformation frictional losses, ferromagnetism Tegoeh Tjahjowidodo

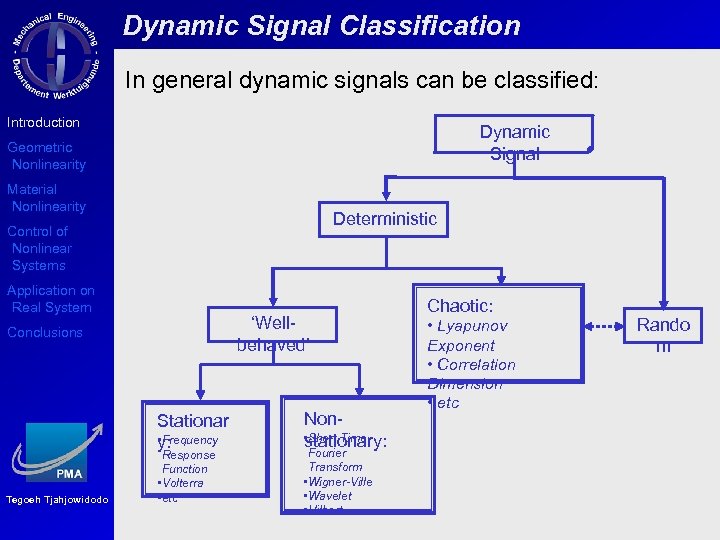Dynamic Signal Classification In general dynamic signals can be classified: Introduction Dynamic Signal Geometric Nonlinearity Material Nonlinearity Deterministic Control of Nonlinear Systems Application on Real System ‘Wellbehaved’ Conclusions Stationar • Frequency y: Tegoeh Tjahjowidodo Response Function • Volterra • etc Non • Short Time stationary: Fourier Transform • Wigner-Ville • Wavelet • Hilbert Chaotic: • Lyapunov Exponent • Correlation Dimension • etc Rando m

Geometric Nonlinearity Tegoeh Tjahjowidodo

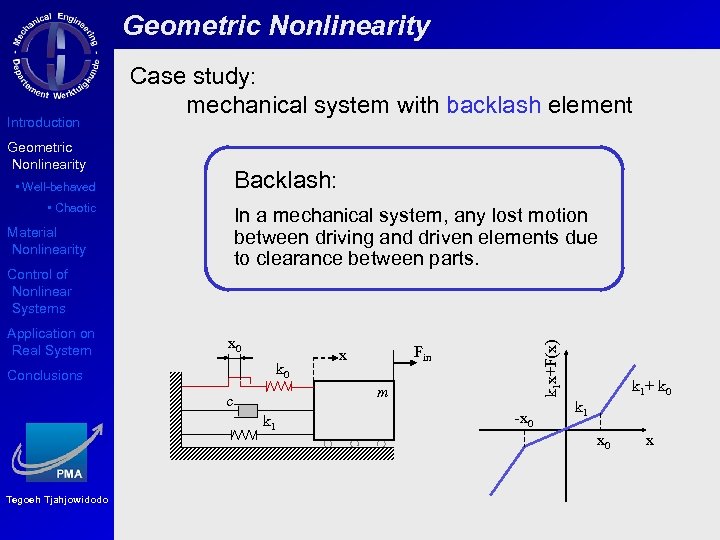Geometric Nonlinearity Backlash: • Well-behaved • Chaotic In a mechanical system, any lost motion between driving and driven elements due to clearance between parts. Material Nonlinearity Control of Nonlinear Systems Application on Real System x 0 k 0 Conclusions Fin x m c k 1 Tegoeh Tjahjowidodo k 1 x+F(x) Introduction Case study: mechanical system with backlash element -x 0 k 1+ k 0 k 1 x 0 x

Backlash Introduction Geometric Nonlinearity Two different cases might appear: • Well-behaved • Chaotic Material Nonlinearity Control of Nonlinear Systems Application on Real System Conclusions – ‘well-behaved’ response for periodic input • Skeleton identification – Hilbert transform – Wavelet analysis – chaotic response for periodic input • Chaos quantification – Lyapunov exponent • Surrogate Data Test Tegoeh Tjahjowidodo

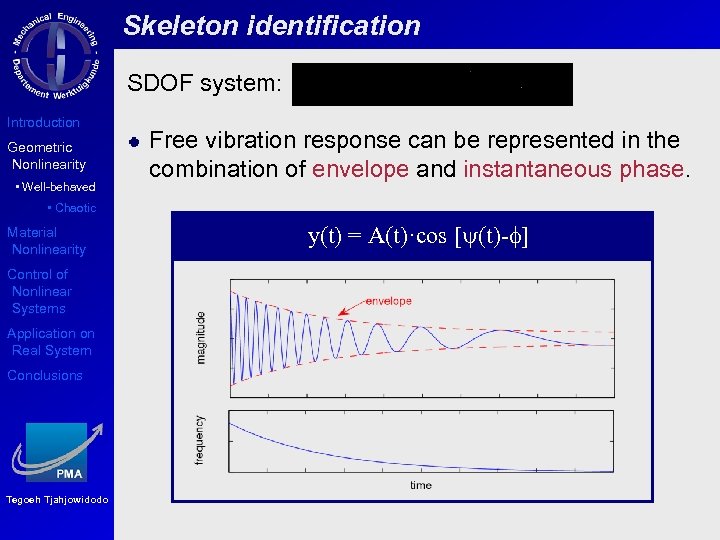Skeleton identification SDOF system: Introduction Geometric Nonlinearity • Well-behaved Free vibration response can be represented in the combination of envelope and instantaneous phase. • Chaotic Material Nonlinearity Control of Nonlinear Systems Application on Real System Conclusions Tegoeh Tjahjowidodo y(t) = A(t)·cos [y(t)-f]

Skeleton identification Introduction Geometric Nonlinearity • Well-behaved • Chaotic Material Nonlinearity Control of Nonlinear Systems Application on Real System Conclusions Tegoeh Tjahjowidodo Envelope and instantaneous phase of the free vibration response can be used as a mechanical signature of the dynamic parameters of the system (Feldman 1994 a).

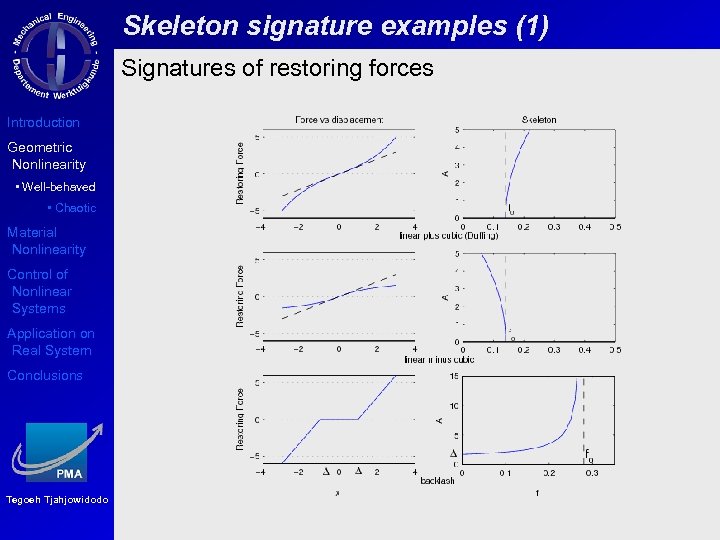Skeleton signature examples (1) Signatures of restoring forces Introduction Geometric Nonlinearity • Well-behaved • Chaotic Material Nonlinearity Control of Nonlinear Systems Application on Real System Conclusions Tegoeh Tjahjowidodo

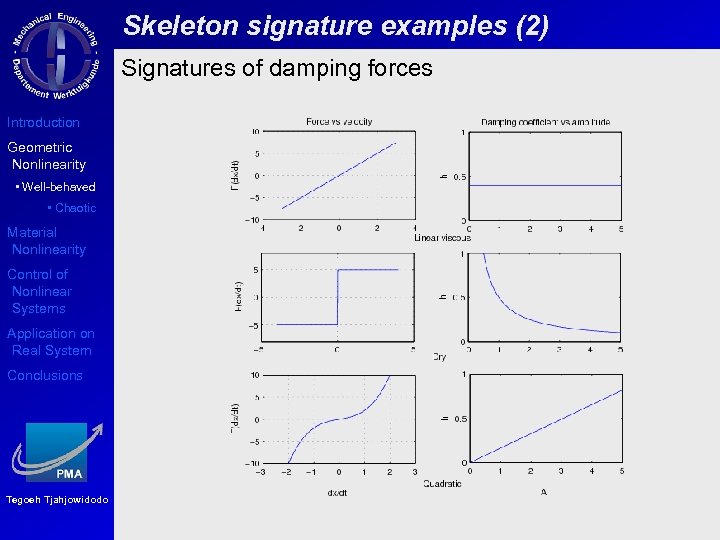Skeleton signature examples (2) Signatures of damping forces Introduction Geometric Nonlinearity • Well-behaved • Chaotic Material Nonlinearity Control of Nonlinear Systems Application on Real System Conclusions Tegoeh Tjahjowidodo

Parameters identification Feldman (1994 a) formulated parameters of the system based on the instantaneous envelope and phase: Introduction Geometric Nonlinearity • Well-behaved • Chaotic Material Nonlinearity Control of Nonlinear Systems Application on Real System Conclusions Tegoeh Tjahjowidodo Extending the method to forced vibration problem, Feldman (1994 b) proposed the following relations:

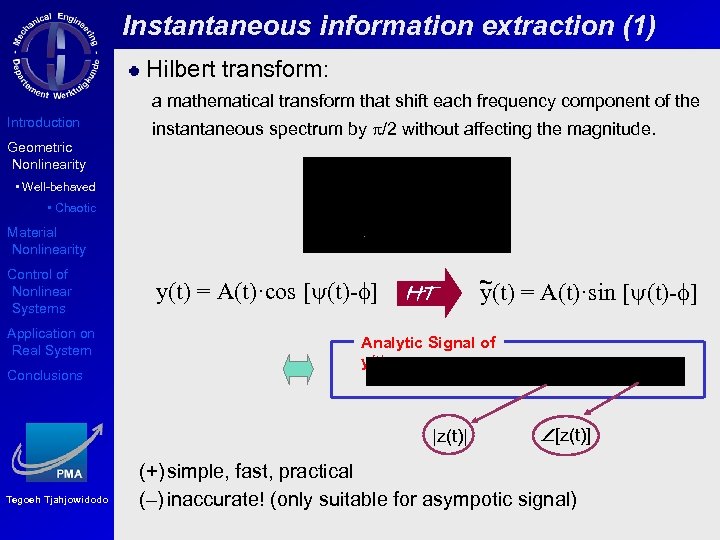Instantaneous information extraction (1) Hilbert transform: a mathematical transform that shift each frequency component of the Introduction instantaneous spectrum by p/2 without affecting the magnitude. Geometric Nonlinearity • Well-behaved • Chaotic Material Nonlinearity Control of Nonlinear Systems Application on Real System Conclusions y(t) = A(t)·cos [y(t)-f] HT Analytic Signal of y(t) |z(t)| Tegoeh Tjahjowidodo ~ = A(t)·sin [y(t)-f] y(t) [z(t)] (+) simple, fast, practical (–) inaccurate! (only suitable for asympotic signal)

Instantaneous information extraction (2) Wavelet transform: a time-frequency representation (TFR) technique Introduction Geometric Nonlinearity • Well-behaved • Chaotic Material Nonlinearity Control of Nonlinear Systems Application on Real System (Complex Morlet Wavelet) instantaneous frequency (in dilation form): envelope wavelet: Conclusions Tegoeh Tjahjowidodo (+) accurate! (–) time consuming, error at the edges, cumbersome in modulus of

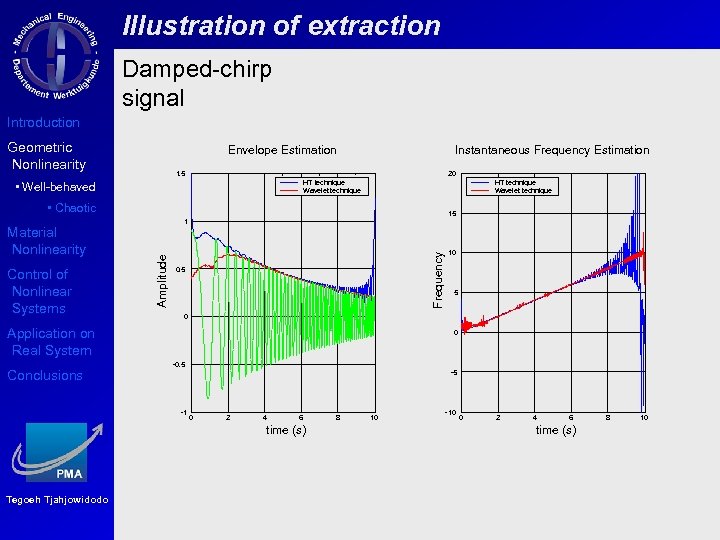Illustration of extraction Damped-chirp signal Introduction Geometric Nonlinearity Envelope Estimation Instantaneous Frequency Estimation 1. 5 20 HT technique Wavelet technique • Well-behaved HT technique Wavelet technique • Chaotic Frequency Control of Nonlinear Systems Amplitude Material Nonlinearity 15 1 0. 5 0 -0. 5 -1 -5 0 2 4 6 time (s) Tegoeh Tjahjowidodo 5 0 Application on Real System Conclusions 10 8 10 -10 0 2 4 6 time (s) 8 10

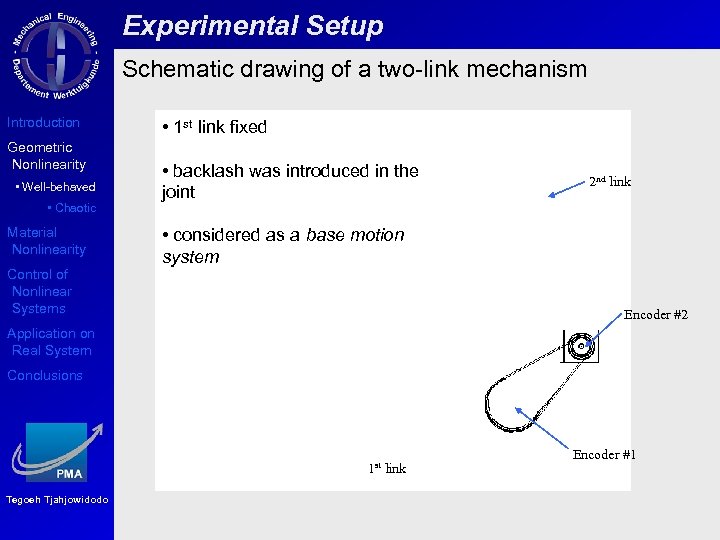Experimental Setup Schematic drawing of a two-link mechanism Introduction Geometric Nonlinearity • Well-behaved • Chaotic Material Nonlinearity Control of Nonlinear Systems • 1 st link fixed • backlash was introduced in the joint 2 nd link • considered as a base motion system Encoder #2 Application on Real System Conclusions 1 st Tegoeh Tjahjowidodo link Encoder #1

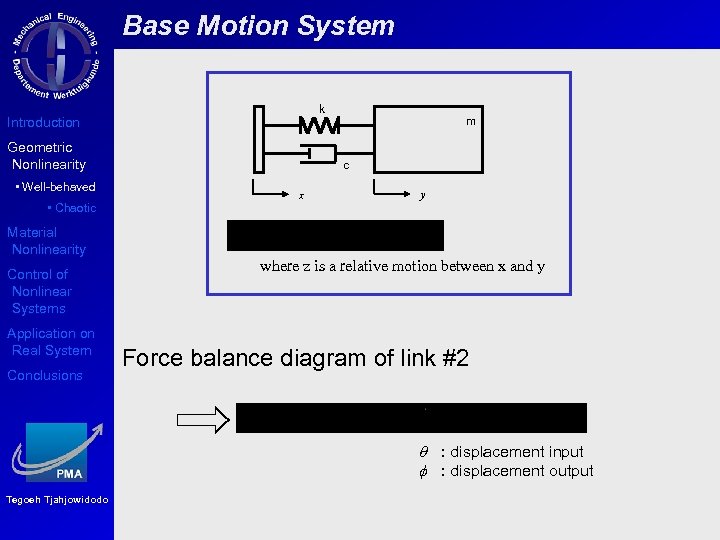Base Motion System k Introduction Geometric Nonlinearity • Well-behaved m c x y • Chaotic Material Nonlinearity Control of Nonlinear Systems Application on Real System Conclusions where z is a relative motion between x and y Force balance diagram of link #2 q : displacement input f : displacement output Tegoeh Tjahjowidodo

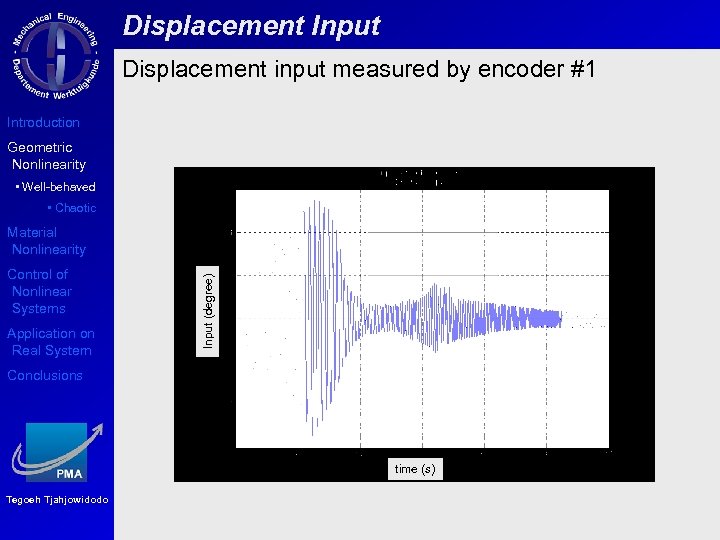Displacement Input Displacement input measured by encoder #1 Introduction Geometric Nonlinearity • Well-behaved • Chaotic Control of Nonlinear Systems Application on Real System Input (degree) Material Nonlinearity Conclusions time (s) Tegoeh Tjahjowidodo

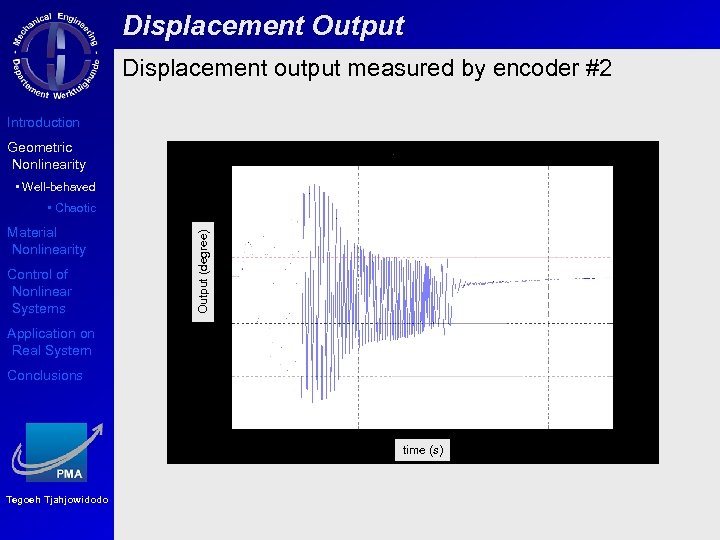Displacement Output Displacement output measured by encoder #2 Introduction Geometric Nonlinearity • Well-behaved Material Nonlinearity Control of Nonlinear Systems Output (degree) • Chaotic Application on Real System Conclusions time (s) Tegoeh Tjahjowidodo

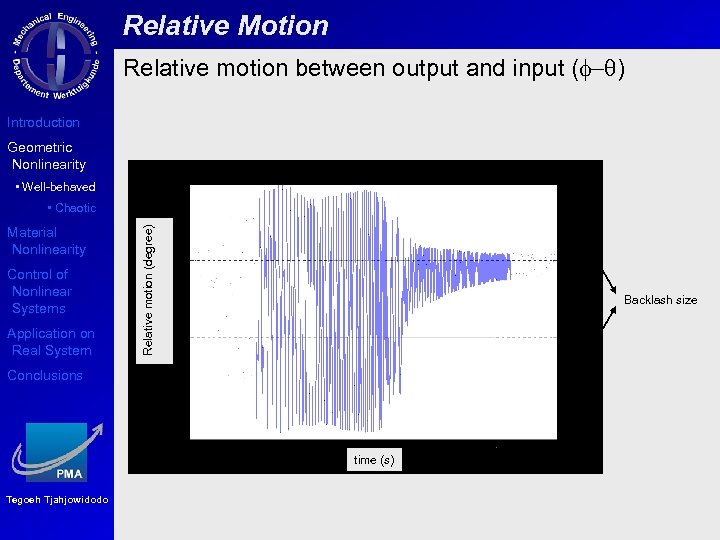Relative Motion Relative motion between output and input (f-q) Introduction Geometric Nonlinearity • Well-behaved Material Nonlinearity Control of Nonlinear Systems Application on Real System Relative motion (degree) • Chaotic Backlash size Conclusions time (s) Tegoeh Tjahjowidodo

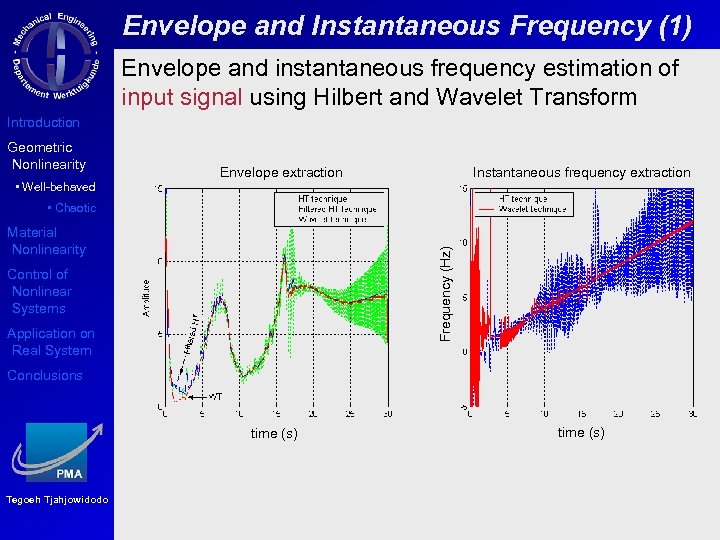Envelope and Instantaneous Frequency (1) Envelope and instantaneous frequency estimation of input signal using Hilbert and Wavelet Transform Introduction Geometric Nonlinearity • Well-behaved Instantaneous frequency extraction Envelope extraction • Chaotic Frequency (Hz) Material Nonlinearity Control of Nonlinear Systems Application on Real System Conclusions time (s) Tegoeh Tjahjowidodo time (s)

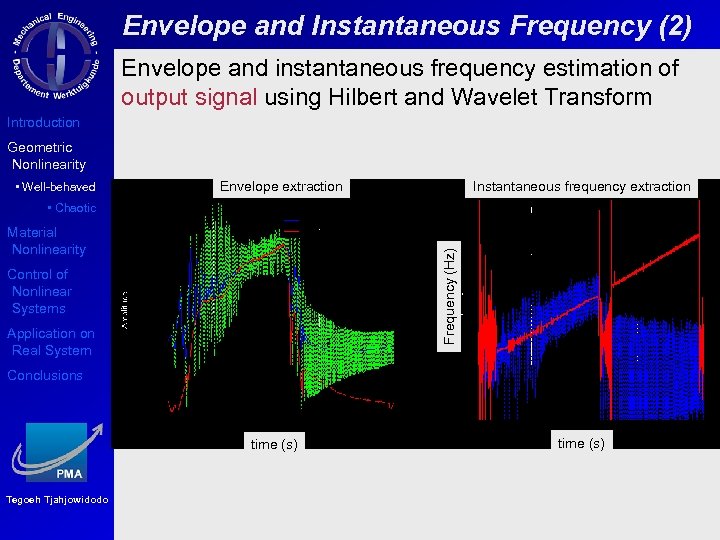Envelope and Instantaneous Frequency (2) Envelope and instantaneous frequency estimation of output signal using Hilbert and Wavelet Transform Introduction Geometric Nonlinearity • Well-behaved Instantaneous frequency extraction Envelope extraction • Chaotic Frequency (Hz) Material Nonlinearity Control of Nonlinear Systems Application on Real System Conclusions time (s) Tegoeh Tjahjowidodo time (s)

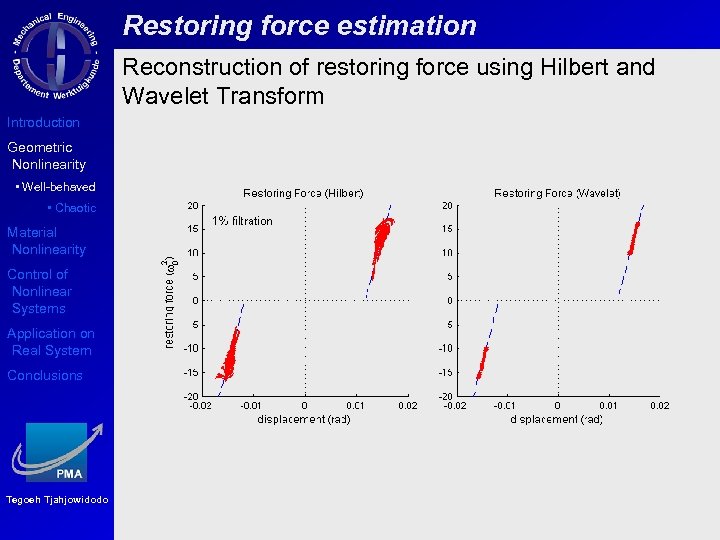Restoring force estimation Reconstruction of restoring force using Hilbert and Wavelet Transform Introduction Geometric Nonlinearity • Well-behaved • Chaotic Material Nonlinearity Control of Nonlinear Systems Application on Real System Conclusions Tegoeh Tjahjowidodo

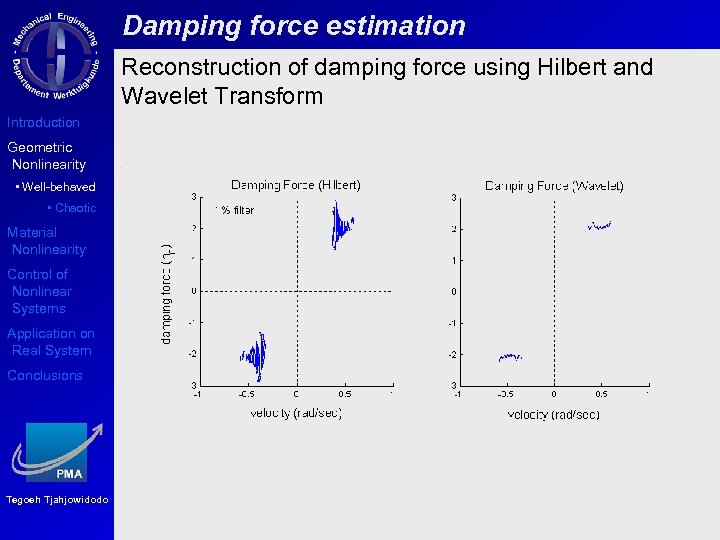Damping force estimation Reconstruction of damping force using Hilbert and Wavelet Transform Introduction Geometric Nonlinearity • Well-behaved • Chaotic Material Nonlinearity Control of Nonlinear Systems Application on Real System Conclusions Tegoeh Tjahjowidodo

Identification on Well-behaved Case Introduction Geometric Nonlinearity • Well-behaved • Chaotic Material Nonlinearity Control of Nonlinear Systems Application on Real System Conclusions Tegoeh Tjahjowidodo Wavelet transform offers better results than the Hilbert transform in skeleton method.

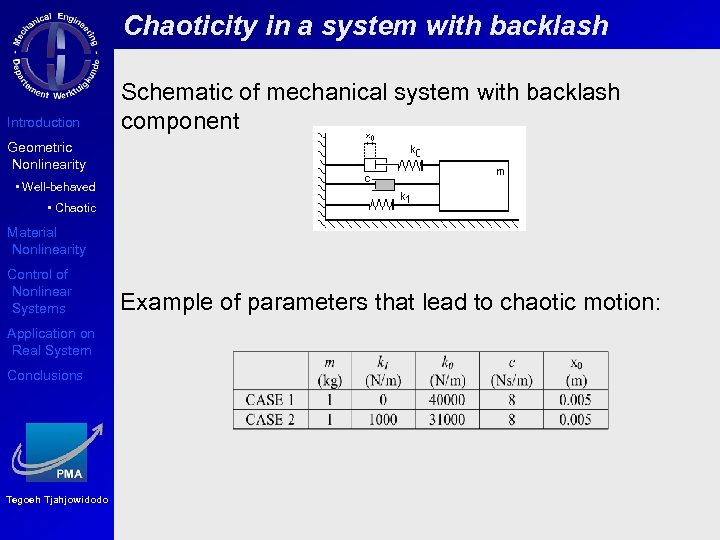Chaoticity in a system with backlash Introduction Schematic of mechanical system with backlash component Geometric Nonlinearity • Well-behaved • Chaotic Material Nonlinearity Control of Nonlinear Systems Application on Real System Conclusions Tegoeh Tjahjowidodo Example of parameters that lead to chaotic motion:

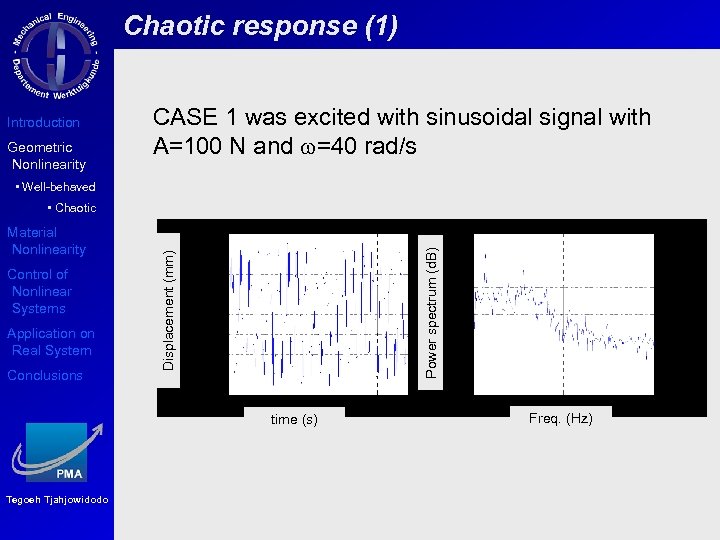Chaotic response (1) Introduction Geometric Nonlinearity CASE 1 was excited with sinusoidal signal with A=100 N and w=40 rad/s • Well-behaved Control of Nonlinear Systems Application on Real System Conclusions Displacement (mm) Material Nonlinearity Power spectrum (d. B) • Chaotic time (s) Tegoeh Tjahjowidodo Freq. (Hz)

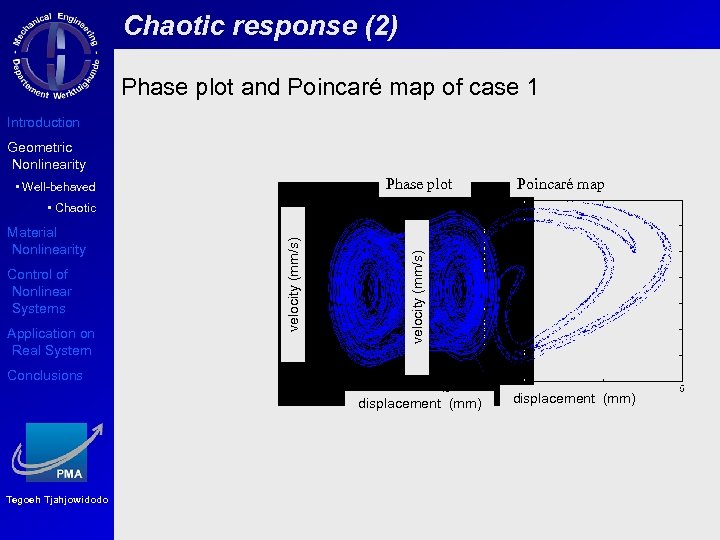Chaotic response (2) Phase plot and Poincaré map of case 1 Introduction Geometric Nonlinearity Phase plot • Well-behaved Poincaré map Control of Nonlinear Systems Application on Real System velocity (mm/s) Material Nonlinearity velocity (mm/s) • Chaotic Conclusions displacement (mm) Tegoeh Tjahjowidodo displacement (mm)

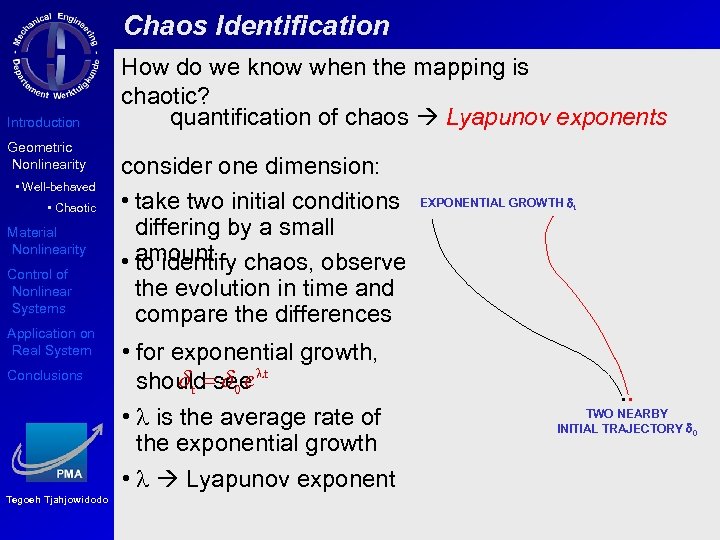Chaos Identification Introduction Geometric Nonlinearity • Well-behaved • Chaotic Material Nonlinearity Control of Nonlinear Systems Application on Real System Conclusions Tegoeh Tjahjowidodo How do we know when the mapping is chaotic? quantification of chaos Lyapunov exponents consider one dimension: • take two initial conditions differing by a small • amount chaos, observe to identify the evolution in time and compare the differences • for exponential growth, dt = d 0 e should see t • is the average rate of the exponential growth • Lyapunov exponent EXPONENTIAL GROWTH dt ▪▪ TWO NEARBY INITIAL TRAJECTORY d 0

Dimensional Analysis Introduction In order to examine the influence of each parameter on the nature of resulting response Geometric Nonlinearity • Well-behaved • Chaotic Material Nonlinearity Control of Nonlinear Systems Application on Real System where: Conclusions primes indicate differentiation with respect to . Tegoeh Tjahjowidodo

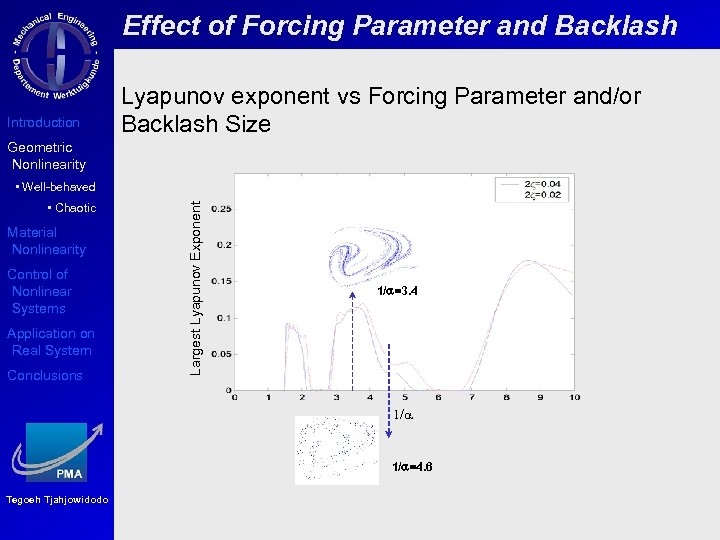Effect of Forcing Parameter and Backlash Introduction Lyapunov exponent vs Forcing Parameter and/or Backlash Size Geometric Nonlinearity • Chaotic Material Nonlinearity Control of Nonlinear Systems Application on Real System Conclusions Largest Lyapunov Exponent • Well-behaved 1/a=3. 4 1/a=4. 6 Tegoeh Tjahjowidodo

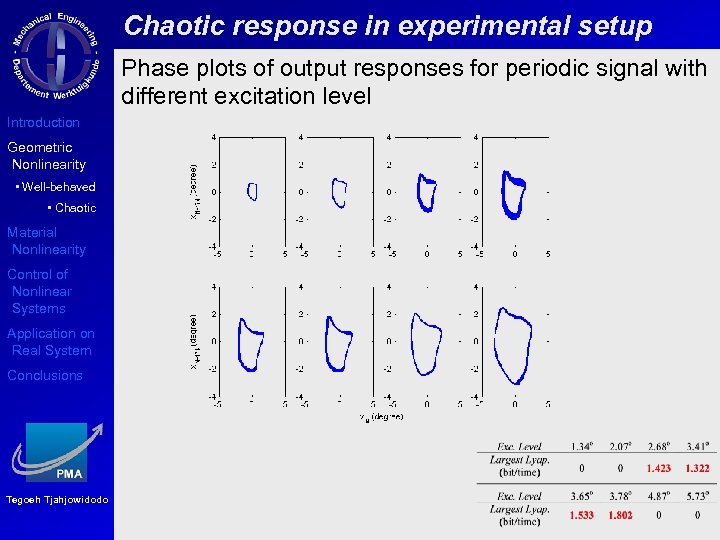Chaotic response in experimental setup Phase plots of output responses for periodic signal with different excitation level Introduction Geometric Nonlinearity • Well-behaved • Chaotic Material Nonlinearity Control of Nonlinear Systems Application on Real System Conclusions Tegoeh Tjahjowidodo

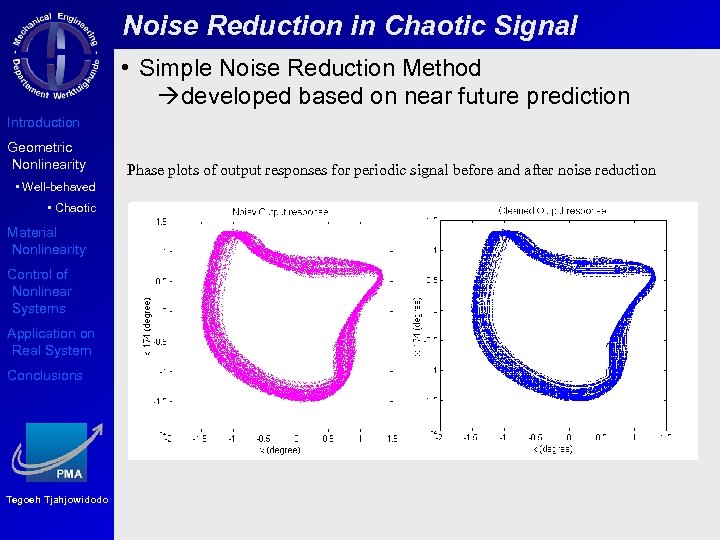Noise Reduction in Chaotic Signal • Simple Noise Reduction Method developed based on near future prediction Introduction Geometric Nonlinearity • Well-behaved • Chaotic Material Nonlinearity Control of Nonlinear Systems Application on Real System Conclusions Tegoeh Tjahjowidodo Phase plots of output responses for periodic signal before and after noise reduction

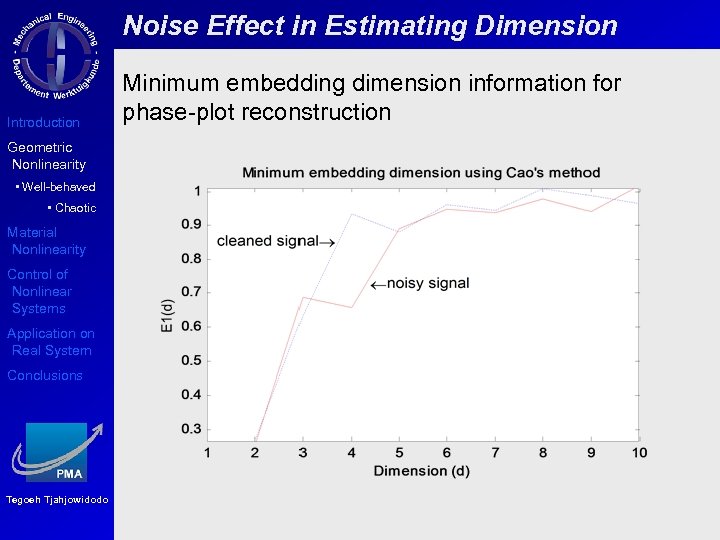Noise Effect in Estimating Dimension Introduction Geometric Nonlinearity • Well-behaved • Chaotic Material Nonlinearity Control of Nonlinear Systems Application on Real System Conclusions Tegoeh Tjahjowidodo Minimum embedding dimension information for phase-plot reconstruction

Identification on Chaotic Case Introduction Geometric Nonlinearity • Well-behaved • Chaotic Material Nonlinearity Control of Nonlinear Systems Application on Real System Conclusions Tegoeh Tjahjowidodo Observing the chaos quantifier, e. g. Lyapunov exponent, could be used, in principle, to estimate the parameter of a system.

Material Nonlinearity Tegoeh Tjahjowidodo

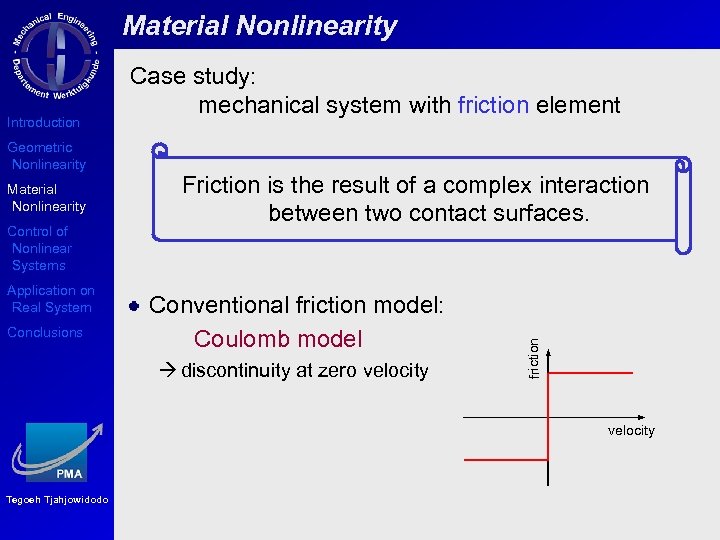Material Nonlinearity Geometric Nonlinearity Material Nonlinearity Control of Nonlinear Systems Application on Real System Conclusions Friction is the result of a complex interaction between two contact surfaces. Conventional friction model: Coulomb model discontinuity at zero velocity friction Introduction Case study: mechanical system with friction element velocity Tegoeh Tjahjowidodo

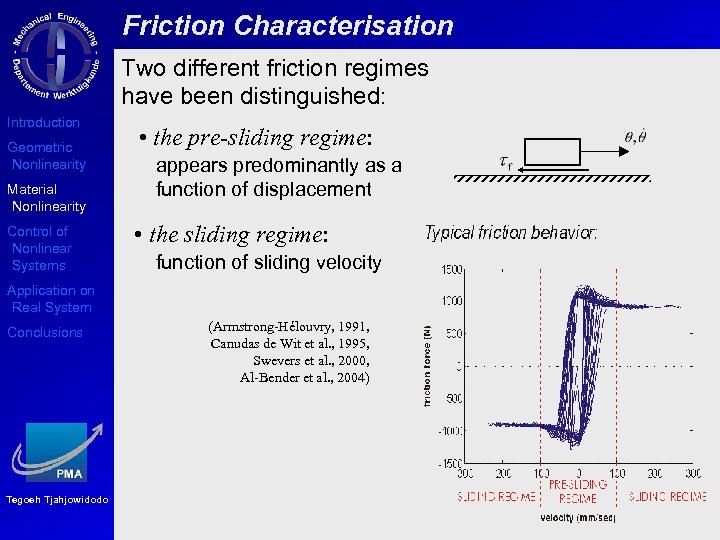Friction Characterisation Two different friction regimes have been distinguished: Introduction Geometric Nonlinearity Material Nonlinearity Control of Nonlinear Systems • the pre-sliding regime: appears predominantly as a function of displacement • the sliding regime: function of sliding velocity Application on Real System Conclusions Tegoeh Tjahjowidodo (Armstrong-Hélouvry, 1991, Canudas de Wit et al. , 1995, Swevers et al. , 2000, Al-Bender et al. , 2004)

Pre-sliding regime (1) Pre-sliding friction Introduction Geometric Nonlinearity Material Nonlinearity Friction force in pre-sliding regime not only depends on the output at some time instant in the past and the input, but also on past extremum values of the input or output as well. hysteresis with non-local memory Control of Nonlinear Systems Friction force Fm x 3 Application on Real System Conclusions 1 y(q) -qm qm 0 -y(-q) 2 4 Tegoeh Tjahjowidodo (displacement) 2 x

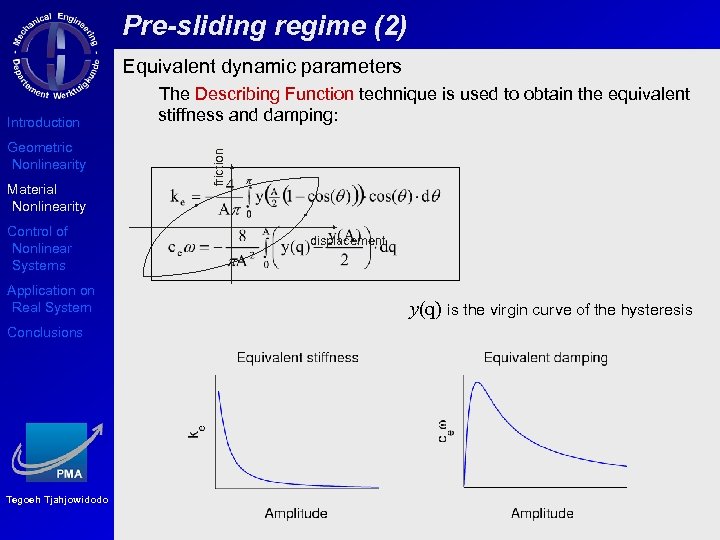Pre-sliding regime (2) Equivalent dynamic parameters Geometric Nonlinearity Material Nonlinearity Control of Nonlinear Systems Application on Real System Conclusions Tegoeh Tjahjowidodo friction Introduction The Describing Function technique is used to obtain the equivalent stiffness and damping: displacement y(q) is the virgin curve of the hysteresis

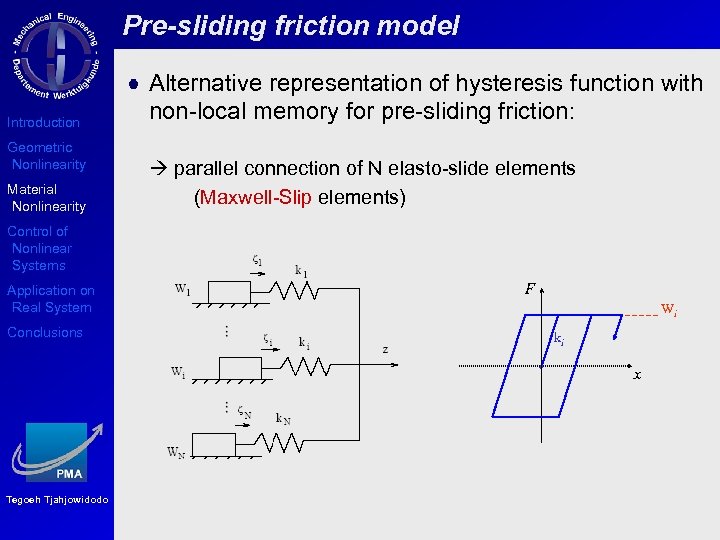Pre-sliding friction model Introduction Geometric Nonlinearity Material Nonlinearity Alternative representation of hysteresis function with non-local memory for pre-sliding friction: parallel connection of N elasto-slide elements (Maxwell-Slip elements) Control of Nonlinear Systems Application on Real System Conclusions F Wi ki x Tegoeh Tjahjowidodo

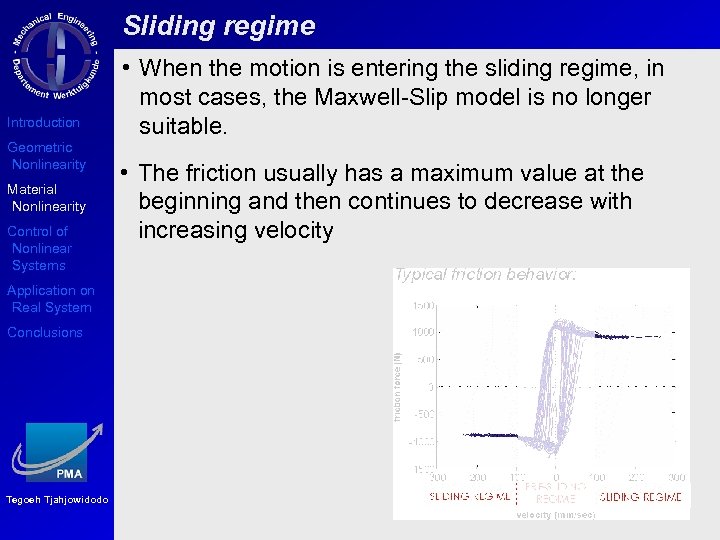Sliding regime Introduction Geometric Nonlinearity Material Nonlinearity Control of Nonlinear Systems Application on Real System Conclusions Tegoeh Tjahjowidodo • When the motion is entering the sliding regime, in most cases, the Maxwell-Slip model is no longer suitable. • The friction usually has a maximum value at the beginning and then continues to decrease with increasing velocity

GMS friction model Generalized Maxwell-Slip (GMS) model Ø developed at PMA/KULeuven Introduction Geometric Nonlinearity Material Nonlinearity – If the model is sticking: Control of Nonlinear Systems Mathematical representation of Maxwell-Slip elements Application on Real System Conclusions – If the model is slipping: Tegoeh Tjahjowidodo

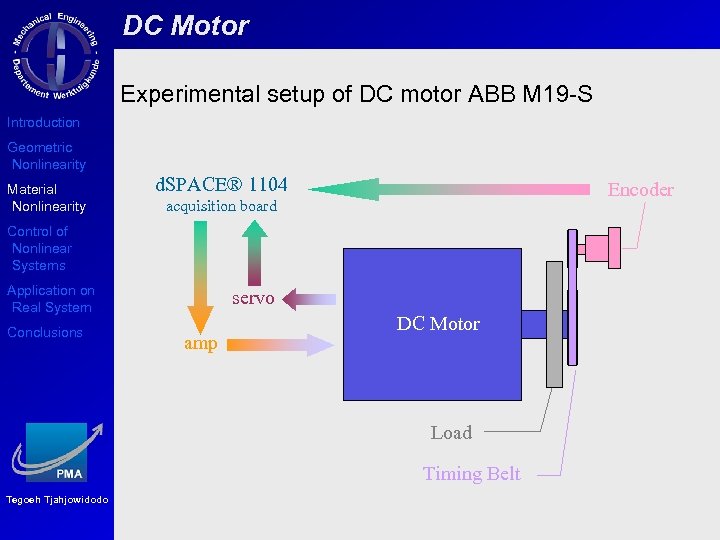DC Motor Experimental setup of DC motor ABB M 19 -S Introduction Geometric Nonlinearity Material Nonlinearity d. SPACE® 1104 Encoder acquisition board Control of Nonlinear Systems Application on Real System Conclusions servo amp DC Motor Load Timing Belt Tegoeh Tjahjowidodo

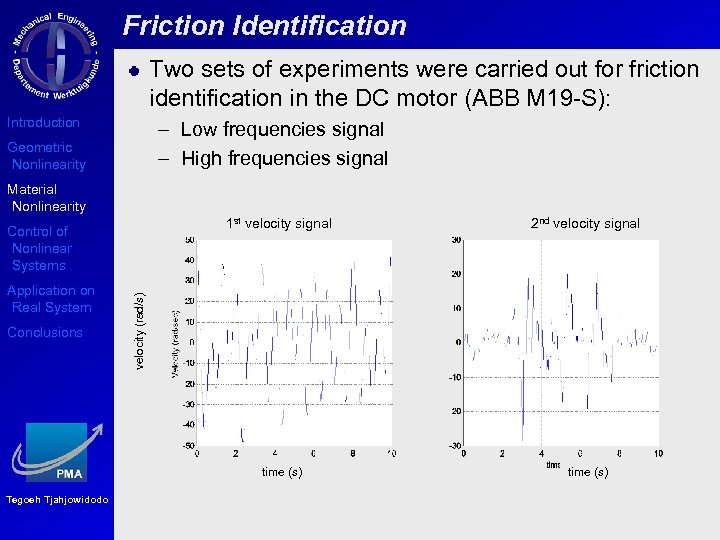Friction Identification Two sets of experiments were carried out for friction identification in the DC motor (ABB M 19 -S): Introduction – Low frequencies signal – High frequencies signal Geometric Nonlinearity Material Nonlinearity 1 st velocity signal Conclusions Tegoeh Tjahjowidodo time (s) velocity (rad/s) Application on Real System 2 nd velocity signal time (s) Control of Nonlinear Systems

Identification Strategy Introduction Geometric Nonlinearity Material Nonlinearity Control of Nonlinear Systems Application on Real System Conclusions Tegoeh Tjahjowidodo Identification technique for the physics-based model: • Genetic Algorithm • Nelder-Mead Downhill Simplex Method The optimization is based upon minimization of cost function:

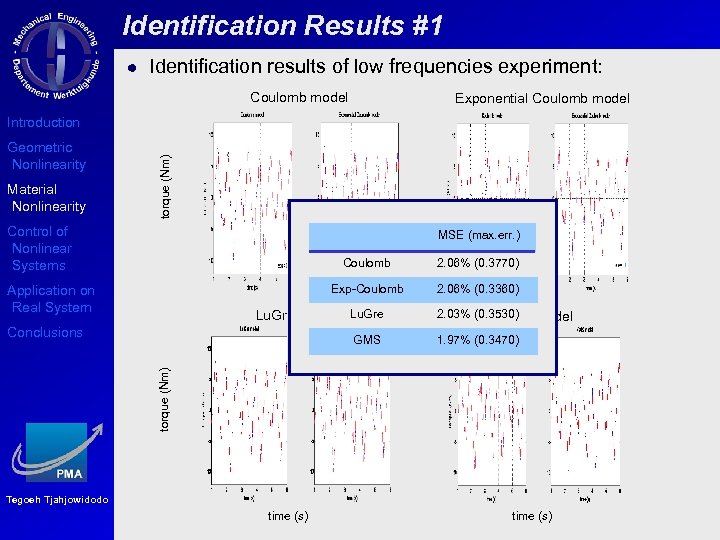Identification Results #1 Identification results of low frequencies experiment: Coulomb model Exponential Coulomb model Geometric Nonlinearity Material Nonlinearity torque (Nm) Introduction Control of Nonlinear Systems MSE (max. err. ) Coulomb Exp-Coulomb Application on Real System 2. 06% (0. 3770) 2. 06% (0. 3360) Lu. Gre model Lu. Gre Conclusions 1. 97% (0. 3470) torque (Nm) GMS 2. 03% (0. 3530) model GMS Tegoeh Tjahjowidodo time (s)

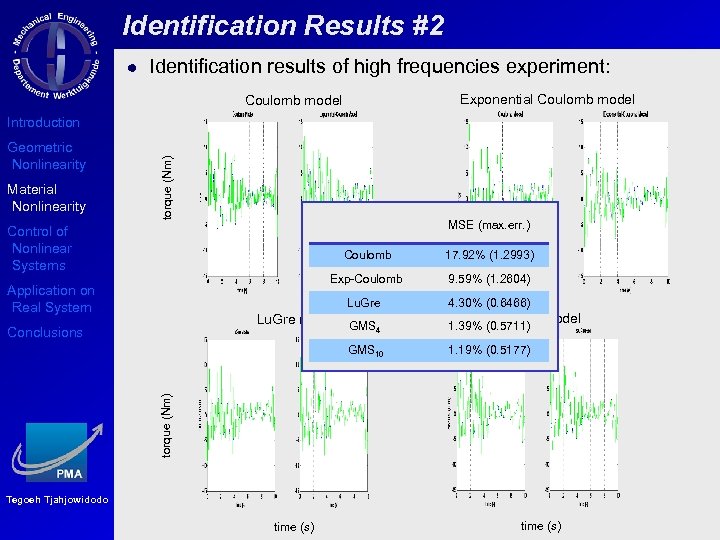Identification Results #2 Identification results of high frequencies experiment: Exponential Coulomb model Geometric Nonlinearity Material Nonlinearity torque (Nm) Introduction MSE (max. err. ) Control of Nonlinear Systems Coulomb Exp-Coulomb 4. 30% (0. 6466) Lu. Gre model GMS 4 1. 39% (0. 5711) GMS 10 1. 19% (0. 5177) GMS model torque (Nm) Conclusions 9. 59% (1. 2604) Lu. Gre Application on Real System 17. 92% (1. 2993) Tegoeh Tjahjowidodo time (s)

Identification on Material Nonlinearity Case Introduction Geometric Nonlinearity Material Nonlinearity Control of Nonlinear Systems Application on Real System Conclusions Tegoeh Tjahjowidodo Friction identification is possible to be conducted using a single experiment. However, selection of the excitation signal plays an important role for the identification step.

Control of Nonlinear Systems Tegoeh Tjahjowidodo

Overview of Controllers Model-based controllers Geometric Nonlinearity Material Nonlinearity Control of Nonlinear Systems Application on Real System Conclusions – Linear Controllers • PD controller • Cascade controller (combine position-speed loops) – Nonlinear Controllers • Discontinuous Nonlinear Proportional Feedback (DNPF) controller adds an extra compensating torque when the position error is within presliding region Control input (u) Introduction -Qh Qh Position error (e) • Gain Scheduling controller developed based on the equivalent dynamic parameters of the system. Tegoeh Tjahjowidodo

Gain Scheduling Controller (1) Introduction Geometric Nonlinearity treats two different regimes of friction in separated modes. q The first mode • when the system is moving in the sliding region • linear controller + equivalent Coulomb friction model q The second mode • when the system is moving in the pre-sliding region • adjusts proportional (kp) and derivative (kd) gain based on the equivalent dynamic parameter Material Nonlinearity Control of Nonlinear Systems Application on Real System Conclusions The corresponding gains are designed and optimized at some points (of amplitude of motion) regarding a certain performance criteria. Tegoeh Tjahjowidodo

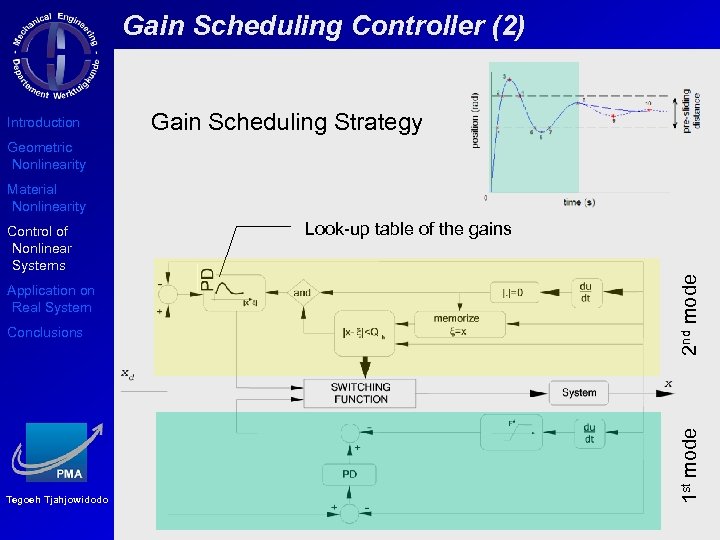Gain Scheduling Controller (2) Introduction Gain Scheduling Strategy Geometric Nonlinearity Material Nonlinearity Conclusions Tegoeh Tjahjowidodo 2 nd mode Application on Real System Look-up table of the gains 1 st mode Control of Nonlinear Systems

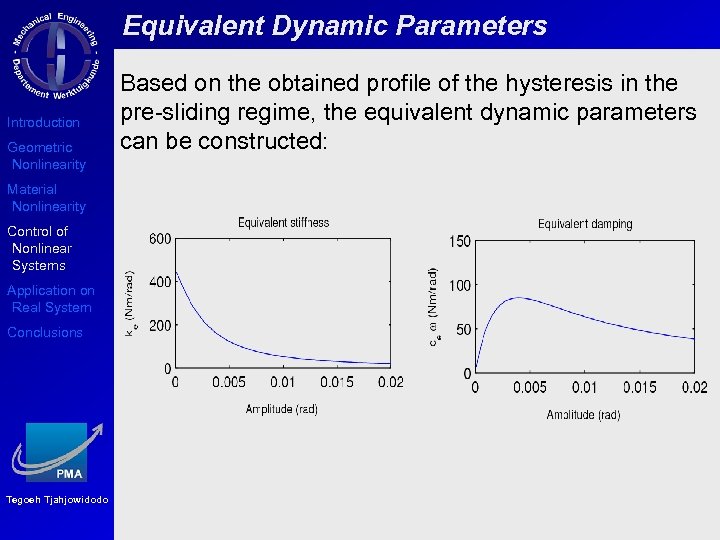Equivalent Dynamic Parameters Introduction Geometric Nonlinearity Material Nonlinearity Control of Nonlinear Systems Application on Real System Conclusions Tegoeh Tjahjowidodo Based on the obtained profile of the hysteresis in the pre-sliding regime, the equivalent dynamic parameters can be constructed:

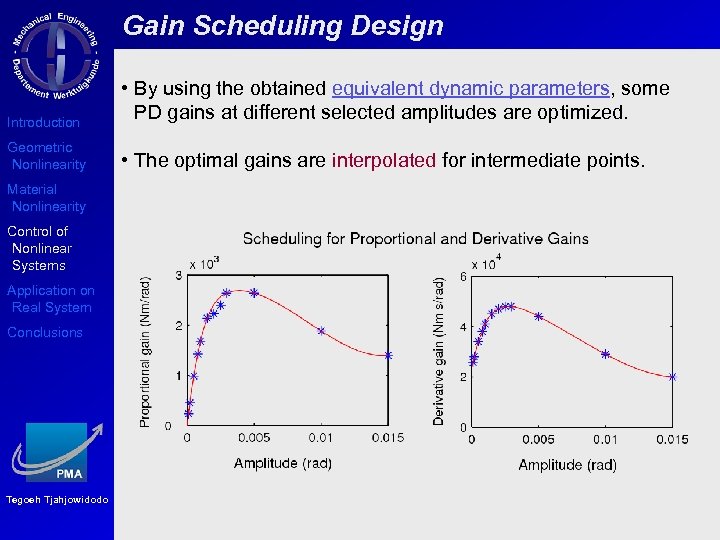Gain Scheduling Design Introduction • By using the obtained equivalent dynamic parameters, some PD gains at different selected amplitudes are optimized. Geometric Nonlinearity • The optimal gains are interpolated for intermediate points. Material Nonlinearity Control of Nonlinear Systems Application on Real System Conclusions Tegoeh Tjahjowidodo

Control Objectives Introduction Performance criteria: Geometric Nonlinearity Material Nonlinearity Control of Nonlinear Systems In the point-to-point (PTP) positioning system, a high accuracy and a short transition time are the most important performance criteria, while the path of the motion is less significant. Application on Real System Conclusions Tegoeh Tjahjowidodo High accuracy and fast response speed with no overshoots are desired.

Step Input Introduction Geometric Nonlinearity Material Nonlinearity Control of Nonlinear Systems The step responses to a 0. 4 rad step input are appraised. Application on Real System Conclusions - Tegoeh Tjahjowidodo

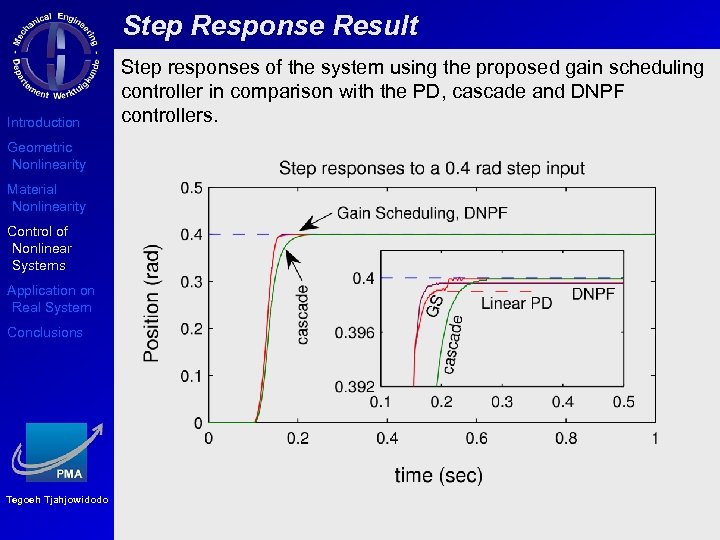Step Response Result Introduction Geometric Nonlinearity Material Nonlinearity Control of Nonlinear Systems Application on Real System Conclusions Tegoeh Tjahjowidodo Step responses of the system using the proposed gain scheduling controller in comparison with the PD, cascade and DNPF controllers.

Control of Nonlinear System Introduction Geometric Nonlinearity Material Nonlinearity Control of Nonlinear Systems Application on Real System Conclusions Tegoeh Tjahjowidodo Model based control is able to yield good results, depending on the models used and the control strategy.

Application on a Real System (Harmonic Drive) Tegoeh Tjahjowidodo

The Harmonic Drive Introduction Invented by C. Walton Musser in 1955. Geometric Nonlinearity Material Nonlinearity Control of Nonlinear Systems Application on Real System • Identification • Control Conclusions Tegoeh Tjahjowidodo Originally labeled ‘strain-wave gearing’, which employs a continuous deflection wave along a nonrigid gear to allow gradual engagement of gear teeth. Can provide very high reduction ratios in a very small package.

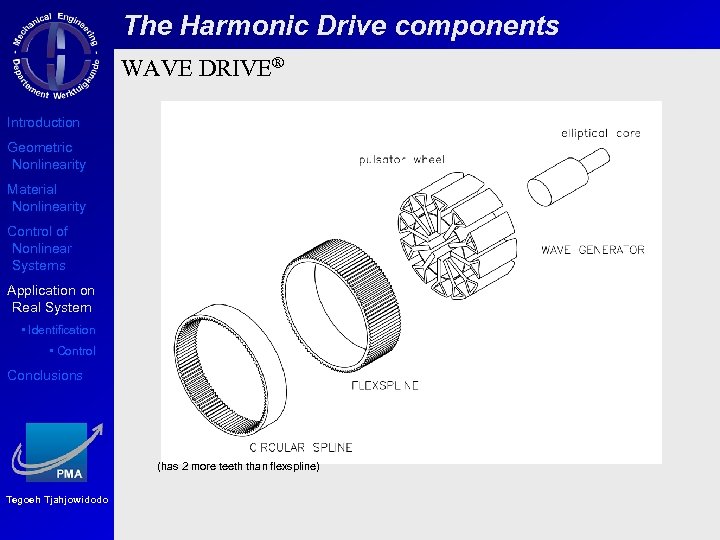The Harmonic Drive components WAVE DRIVE® Introduction Geometric Nonlinearity Material Nonlinearity Control of Nonlinear Systems Application on Real System • Identification • Control Conclusions (has 2 more teeth than flexspline) Tegoeh Tjahjowidodo

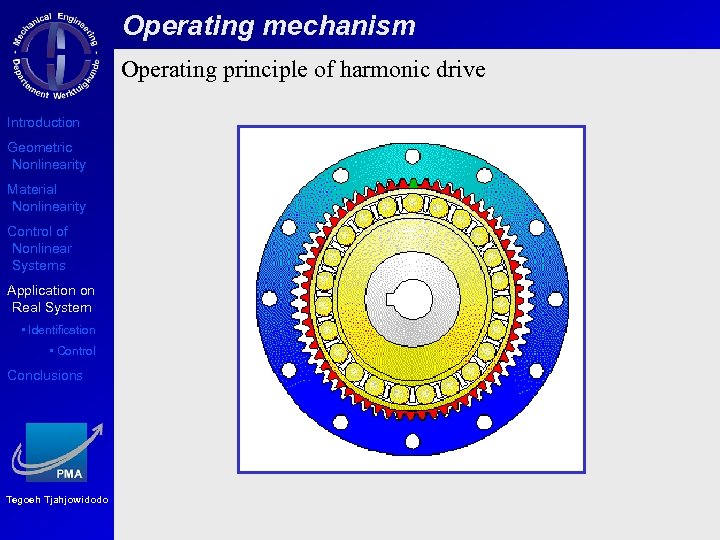Operating mechanism Operating principle of harmonic drive Introduction Geometric Nonlinearity Material Nonlinearity Control of Nonlinear Systems Application on Real System • Identification • Control Conclusions Tegoeh Tjahjowidodo

Scope of Harmonic Drive Research Introduction Geometric Nonlinearity Material Nonlinearity Control of Nonlinear Systems Application on Real System • Identification • Control Conclusions Tegoeh Tjahjowidodo Torsional Stiffness: – apparently due to deformation of the wave generator, and an increase in gear-tooth contact area with increasing load (Nye, 1991). – displays a ‘soft wind-up’ behavior, which is characterized by very low stiffness at low applied load (Kircanski, 1997). Frictional Losses: – occurs primarily at the gear-tooth interface – Friction in Harmonic Drive is strongly position dependent due to kinematic error (Kennedy, 2003). Kinematic error: – caused by a number of factors, such as tooth-placement errors, out-ofroundness in HD components, and misalignment during assembly. – The error signature can display frequency components at two cycles per wave-generator revolution (Tuttle, 1992).

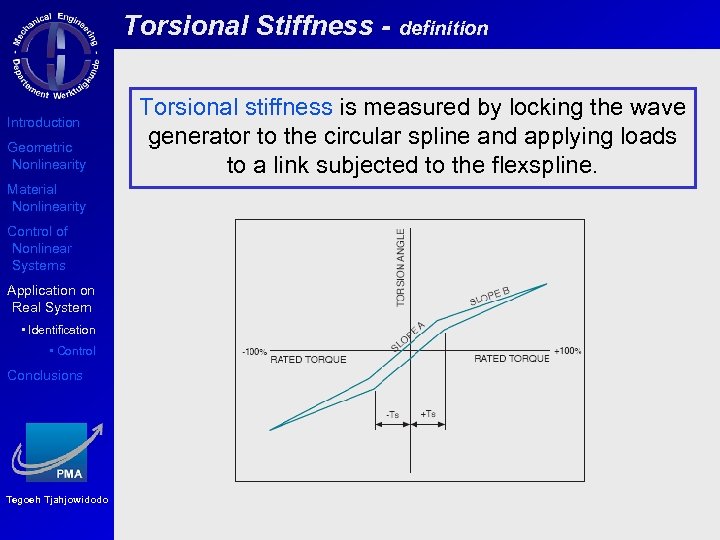Torsional Stiffness - definition Introduction Geometric Nonlinearity Material Nonlinearity Control of Nonlinear Systems Application on Real System • Identification • Control Conclusions Tegoeh Tjahjowidodo Torsional stiffness is measured by locking the wave generator to the circular spline and applying loads to a link subjected to the flexspline.

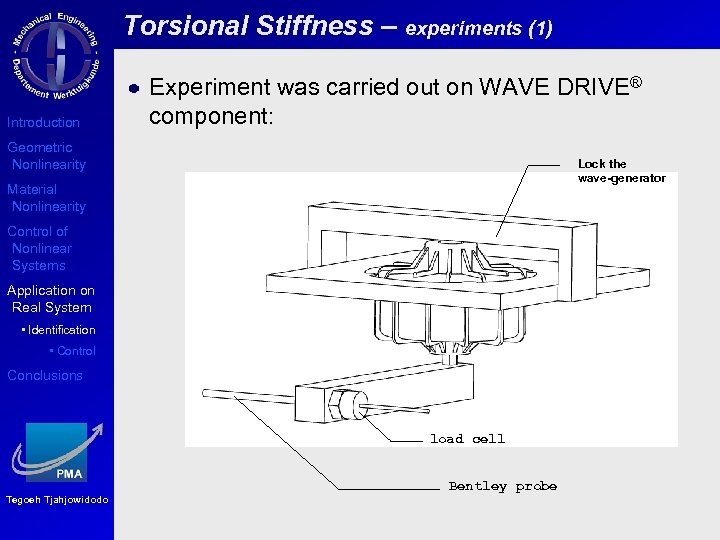Torsional Stiffness – experiments (1) Introduction Experiment was carried out on WAVE DRIVE® component: Geometric Nonlinearity Lock the wave-generator Material Nonlinearity Control of Nonlinear Systems Application on Real System • Identification • Control Conclusions load cell Tegoeh Tjahjowidodo Bentley probe

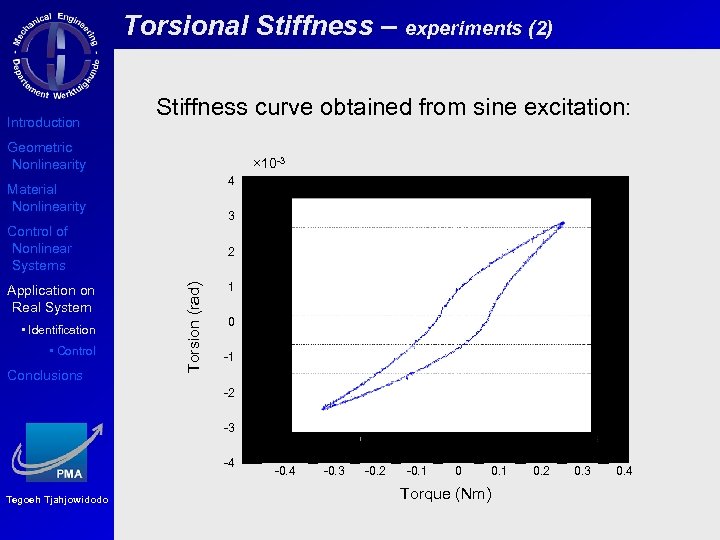Torsional Stiffness – experiments (2) Introduction Stiffness curve obtained from sine excitation: Geometric Nonlinearity × 10 -3 4 Material Nonlinearity 3 Control of Nonlinear Systems • Identification • Control Conclusions Torsion (rad) Application on Real System 2 1 0 -1 -2 -3 -4 Tegoeh Tjahjowidodo -0. 4 -0. 3 -0. 2 -0. 1 0 Torque (Nm) 0. 1 0. 2 0. 3 0. 4

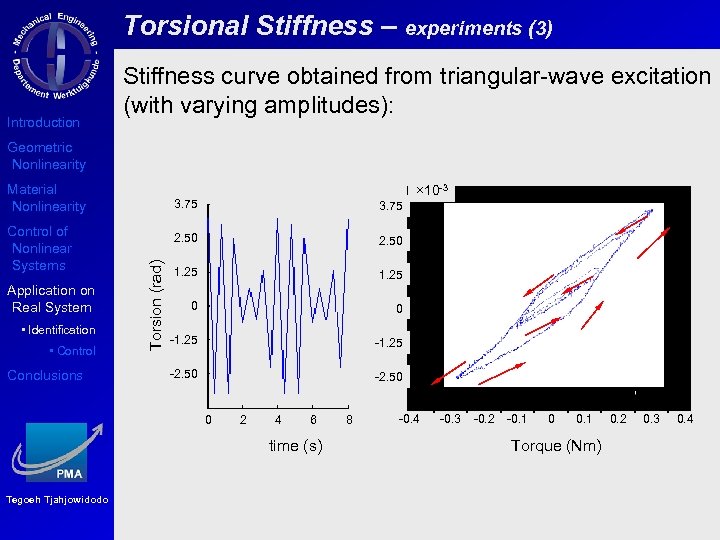Torsional Stiffness – experiments (3) Introduction Stiffness curve obtained from triangular-wave excitation (with varying amplitudes): Geometric Nonlinearity Material Nonlinearity Application on Real System • Identification • Control Conclusions 3. 75 2. 50 Torsion (rad) Control of Nonlinear Systems × 10 -3 2. 50 1. 25 0 0 -1. 25 -2. 50 0 2 4 6 time (s) Tegoeh Tjahjowidodo 8 -0. 4 -0. 3 -0. 2 -0. 1 0 0. 1 Torque (Nm) 0. 2 0. 3 0. 4

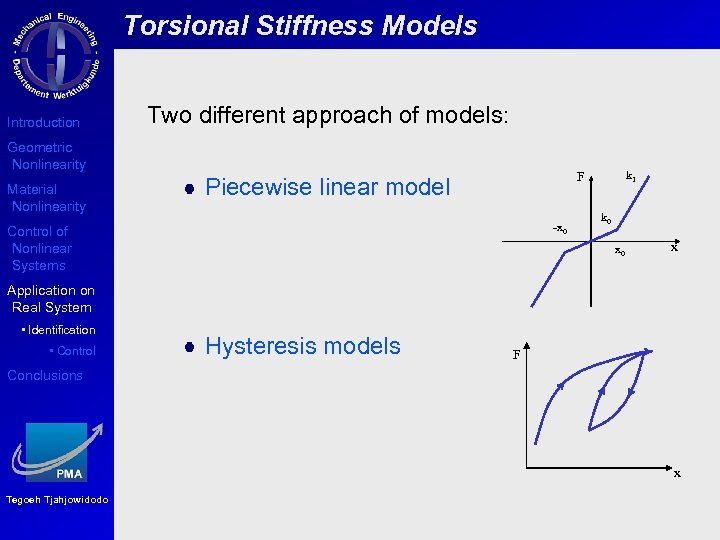Torsional Stiffness Models Introduction Two different approach of models: Geometric Nonlinearity Material Nonlinearity k 1 F Piecewise linear model -x 0 Control of Nonlinear Systems k 0 x Application on Real System • Identification • Control Hysteresis models F Conclusions x Tegoeh Tjahjowidodo

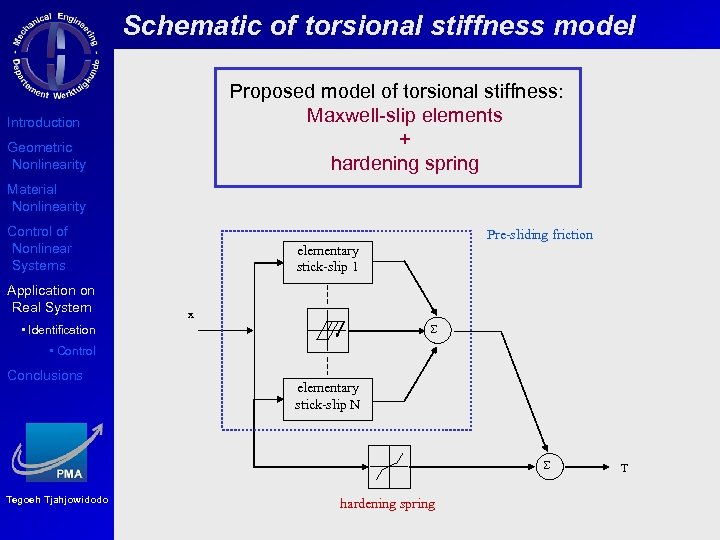Schematic of torsional stiffness model Proposed model of torsional stiffness: Maxwell-slip elements + hardening spring Introduction Geometric Nonlinearity Material Nonlinearity Control of Nonlinear Systems Application on Real System Pre-sliding friction elementary stick-slip 1 x S • Identification • Control Conclusions elementary stick-slip N S Tegoeh Tjahjowidodo hardening spring T

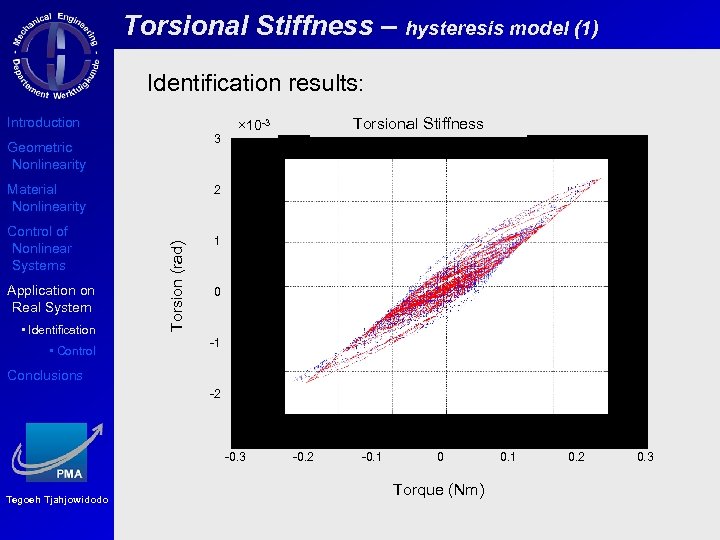Torsional Stiffness – hysteresis model (1) Identification results: Introduction 3 Geometric Nonlinearity Material Nonlinearity Application on Real System • Identification • Control 2 Torsion (rad) Control of Nonlinear Systems Torsional Stiffness × 10 -3 1 0 -1 Conclusions -2 -0. 3 Tegoeh Tjahjowidodo -0. 2 -0. 1 0 Torque (Nm) 0. 1 0. 2 0. 3

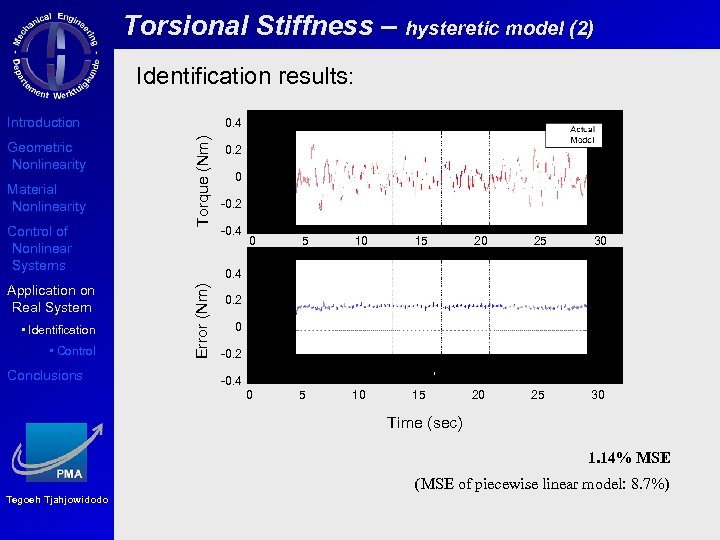Torsional Stiffness – hysteretic model (2) Identification results: Introduction Material Nonlinearity Control of Nonlinear Systems Torque (Nm) Geometric Nonlinearity 0. 4 0. 2 0 -0. 2 -0. 4 • Control Conclusions 10 15 20 25 30 5 10 15 20 25 30 0. 4 Error (Nm) • Identification 5 0 Application on Real System 0 0. 2 0 -0. 2 -0. 4 Time (sec) 1. 14% MSE (MSE of piecewise linear model: 8. 7%) Tegoeh Tjahjowidodo

Control of Mechanical System with HD System apparatus: Introduction Geometric Nonlinearity Material Nonlinearity Control of Nonlinear Systems Application on Real System • Identification • Control Conclusions Tegoeh Tjahjowidodo FHA-C mini servo actuator gear set with AC servo motor in one compact package

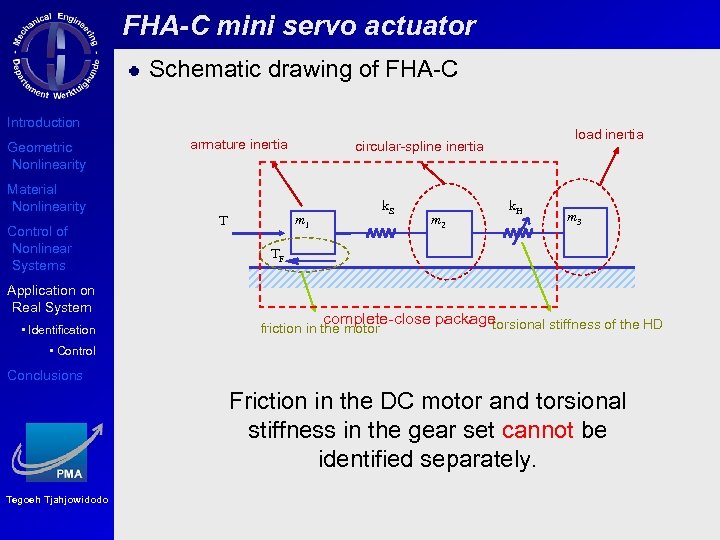FHA-C mini servo actuator Schematic drawing of FHA-C Introduction Geometric Nonlinearity Material Nonlinearity Control of Nonlinear Systems Application on Real System • Identification armature inertia k. S m 1 T load inertia circular-spline inertia m 2 k. H m 3 TF complete-close package torsional stiffness of the HD friction in the motor • Control Conclusions Friction in the DC motor and torsional stiffness in the gear set cannot be identified separately. Tegoeh Tjahjowidodo

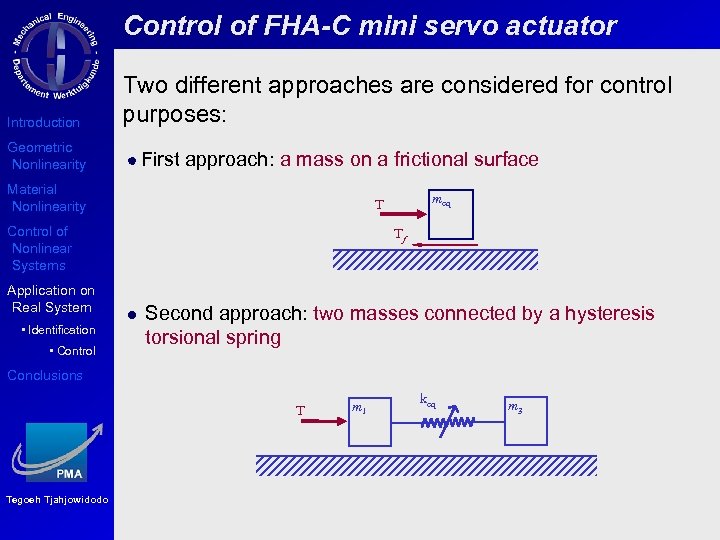Control of FHA-C mini servo actuator Introduction Geometric Nonlinearity Two different approaches are considered for control purposes: First approach: a mass on a frictional surface Material Nonlinearity Control of Nonlinear Systems Application on Real System • Identification • Control meq T Tf Second approach: two masses connected by a hysteresis torsional spring Conclusions T Tegoeh Tjahjowidodo m 1 keq m 3

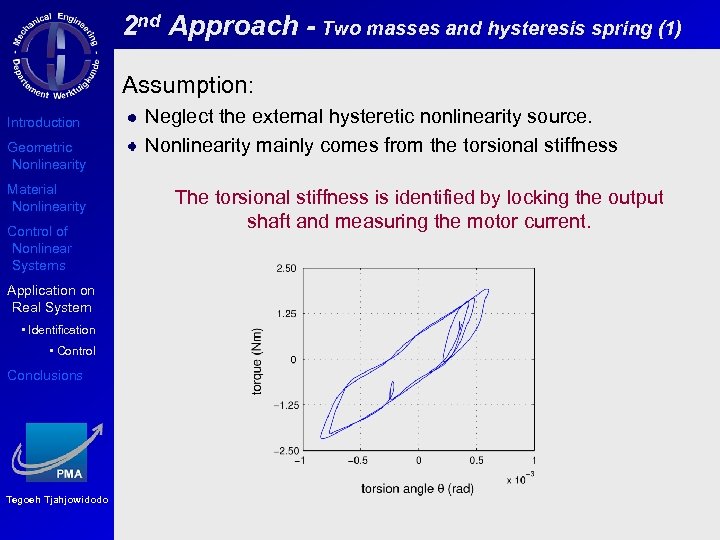2 nd Approach - Two masses and hysteresis spring (1) Assumption: Introduction Geometric Nonlinearity Material Nonlinearity Control of Nonlinear Systems Application on Real System • Identification • Control Conclusions Tegoeh Tjahjowidodo Neglect the external hysteretic nonlinearity source. Nonlinearity mainly comes from the torsional stiffness The torsional stiffness is identified by locking the output shaft and measuring the motor current.

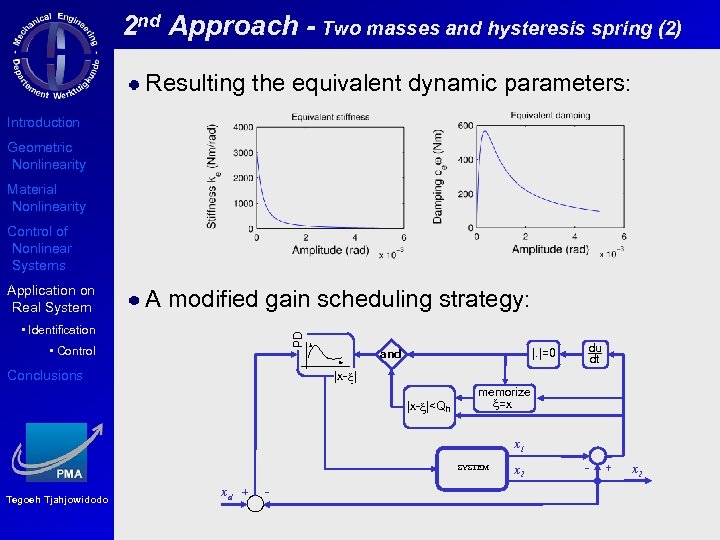2 nd Approach - Two masses and hysteresis spring (2) Resulting the equivalent dynamic parameters: Introduction Geometric Nonlinearity Material Nonlinearity Control of Nonlinear Systems Application on Real System A modified gain scheduling strategy: PD • Identification • Control Conclusions |. |=0 and du dt |x- x| |x-x|

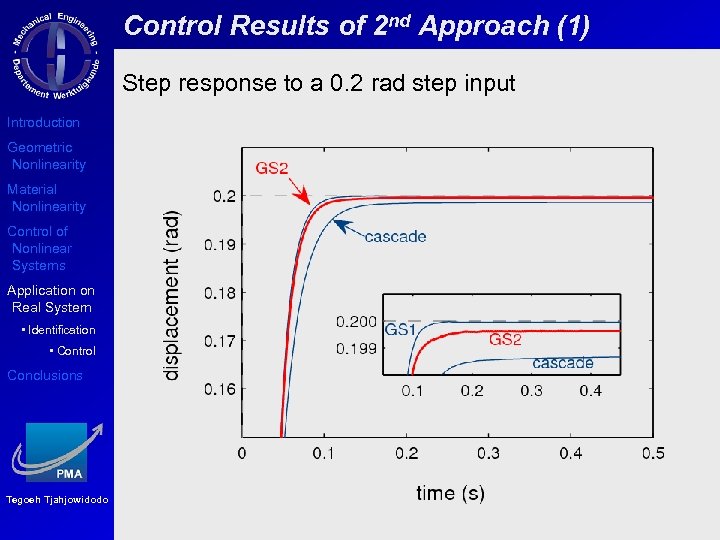Control Results of 2 nd Approach (1) Step response to a 0. 2 rad step input Introduction Geometric Nonlinearity Material Nonlinearity Control of Nonlinear Systems Application on Real System • Identification • Control Conclusions Tegoeh Tjahjowidodo

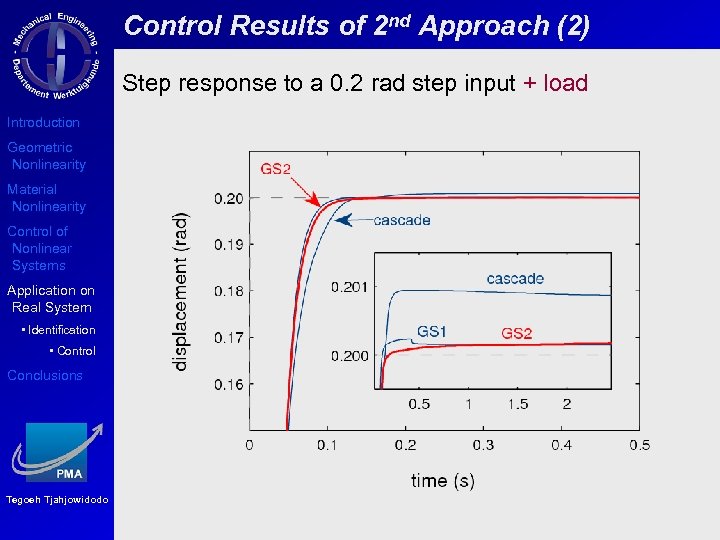Control Results of 2 nd Approach (2) Step response to a 0. 2 rad step input + load Introduction Geometric Nonlinearity Material Nonlinearity Control of Nonlinear Systems Application on Real System • Identification • Control Conclusions Tegoeh Tjahjowidodo

Application on a System with HD Introduction Geometric Nonlinearity Material Nonlinearity Control of Nonlinear Systems Application on Real System • Identification • Control Conclusions Tegoeh Tjahjowidodo A piecewise linear model together with non-local memory hysteresis resolve the difficulties in determining the model of torsional stiffness in harmonic drive.

Conclusions Introduction Geometric Nonlinearity Material Nonlinearity Control of Nonlinear Systems Application on Real System Conclusions Tegoeh Tjahjowidodo Two cases for a nonlinear system with ‘wellbehaved’ and chaotic response for a periodic input have been addressed and appropriate identification methods are developed for each. Identification of systems with material nonlinearity (friction) utilizing single experiment is feasible to be carried out. Detailed understanding of a physical system is playing an important role in achieving a controller with high performance. Identification of a system, in which the two nonlinearity sources are manifested, has been conducted successfully.

Future work Introduction Geometric Nonlinearity Material Nonlinearity Control of Nonlinear Systems Application on Real System Conclusions Tegoeh Tjahjowidodo Combining the advantages of Hilbert and wavelet transform in order to improve the skeleton techniques. Implementation of the skeleton technique for a real higher-degree-of-freedom system. Further study for the applicability of the GMS model to any friction conditions. Extension of the identification and control methods to higher-degree-of-freedom systems with two (or more) hysteresis (material) nonlinearities.

Introduction Geometric Nonlinearity Material Nonlinearity Control of Nonlinear Systems Application on Real System Conclusions Tegoeh Tjahjowidodo