Днепропетровский национальный университет железнодорожного транспорта имени академика В

Днепропетровский национальный университет железнодорожного транспорта имени академика В. Лазаряна Базы данных Кафедра Компьютерные информационные технологии, Швец Олег Михайлович

Нормализация ● ● ● Процесс нормализации Понятие функциональных зависимостей Правила вывода ФЗ Декомпозиция без потерь Первая, вторая и третья нормальные формы Нормальная форма Бойса-Кодда Databases => Normalization 2

Нормализация ● ● ● Процесс нормализации Понятие функциональных зависимостей Правила вывода ФЗ Декомпозиция без потерь Первая, вторая и третья нормальные формы Нормальная форма Бойса-Кодда Databases => Normalization 3

Процесс нормализации ● ● ● Процесс нормализации основывается на концепции нормальных форм Говорят, что отношение находится в определенной нормальной форме, если оно удовлетворяет заданному набору условий Первые три нормальные формы были описаны Э. Коддом Следующую формулу вывели Р. Бойс и Э. Кодд (НФБК – нормальная форма Бойса. Кодда) Четвёртую и пятую нормальные формы определил Р. Фейгин Databases => Normalization 4

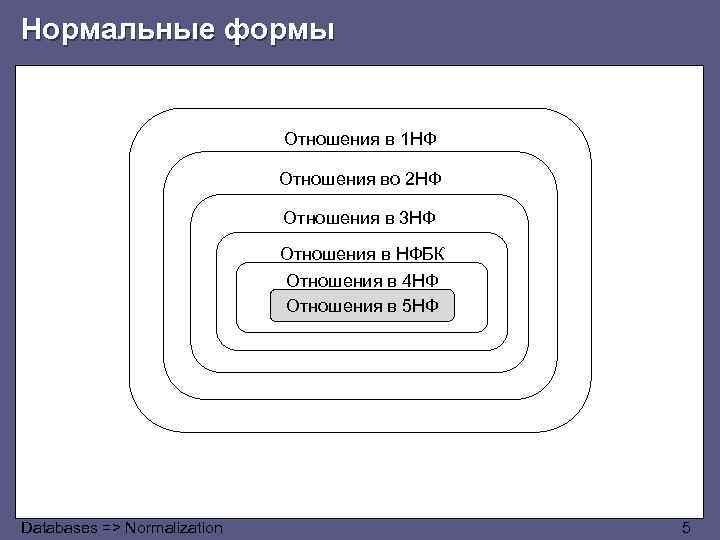Нормальные формы Отношения в 1 НФ Отношения во 2 НФ Отношения в 3 НФ Отношения в НФБК Отношения в 4 НФ Отношения в 5 НФ Databases => Normalization 5

Нормальные формы ● ● Отношение в некоторой нормальной форме предусматривает приведение его к предыдущей нормальной форме Понятия первых нормальных форм основано на функциональных зависимостях (ФЗ) и процессе декомпозиции Databases => Normalization 6

Нормализация ● ● ● Процесс нормализации Понятие функциональных зависимостей Правила вывода ФЗ Декомпозиция без потерь Первая, вторая и третья нормальные формы Нормальная форма Бойса-Кодда Databases => Normalization 7

Понятие функциональных зависимостей (ФЗ) ● ● Пусть R – переменная отношения X и Y – произвольные подмножества атрибутов R Тогда Y функционально зависит от X (X → Y, «X функционально определяет Y» ) тогда и только тогда, когда для любого допустимого значения R каждое значение X связано точно с одним значением Y X называют детерминантом ФЗ, а Y – зависимой частью ФЗ Databases => Normalization 8

Функциональные зависимости. Пример ● ● ● Пусть R – это отношение Students, X – код студента, а Y – множество всех атрибутов студента Тогда X → Y, т. к. X представляет собой первичный ключ, который уникально идентифицирует запись в таблице Students Такое утверждение будет верно и для более общего случая: если X – это потенциальный ключ, то множество всех атрибутов R всегда функционально зависит от X Databases => Normalization 9

Понятие функциональных зависимостей ● ● Однако, следует иметь в виду, что если в R имеется ФЗ, левая часть которой не включает потенциальный ключ, то R обладает избыточностью, что затрудняет обеспечение целостности данных и занимает лишние ресурсы системы Если ни один атрибут не может быть опущен из левой части, то такая функциональная зависимость называется неприводимой (точнее неприводимой слева) Databases => Normalization 10

Неприводимые ФЗ Множество функциональных зависимостей называется неприводимым тогда и только тогда, когда оно обладает тремя свойствами: ● зависимая часть каждой ФЗ содержит только один атрибут ● детерминант каждой ФЗ является неприводимым ● ни одна ФЗ из множества не может быть удалена без потери информации о связях Databases => Normalization 11

Виды ФЗ ● Выделяют два вида функциональных зависимостей: o o ● тривиальные ФЗ нетривиальные ФЗ Тривиальные ФЗ – это ФЗ, в которых правая часть (Y) является подмножеством левой части (X) o С практической точки зрения они не представляют значительного интереса, однако с точки зрения формальной теории зависимостей необходимо учитывать их наличие Нетривиальные ФЗ. Они действительно являются ограничениями целостности Databases => Normalization данных, поэтому в дальнейшем мы будем ● 12

Нормализация ● ● ● Процесс нормализации Понятие функциональных зависимостей Правила вывода ФЗ Декомпозиция без потерь Первая, вторая и третья нормальные формы Нормальная форма Бойса-Кодда Databases => Normalization 13

Правила вывода ФЗ ● ● Для определения того, в какой нормальной форме находится отношение, требуется найти все ФЗ Существуют три правила Армстронга, позволяющие из начального множества ФЗ вывести возможные ФЗ Databases => Normalization 14

Правила вывода ФЗ Пусть A, B, C – это подмножества атрибутов отношения R, AB – объединение этих подмножеств 1. Правило рефлексивности Если множество B является подмножеством множества А, то А → В (по сути, это определение тривиальной зависимости) 2. Правило дополнения Если А → B, то АС → ВС 3. Правило транзитивности Если А → B и B→C, то А → С ● В целях упрощения получения всех ФЗ можно вывести еще несколько дополнительных Databases => Normalization 15 ●

Дополнительные правила вывода ФЗ Пусть D – это еще одно произвольное подмножество множества атрибутов R 4. Правило самоопределения А → А 5. Правило декомпозиции Если А → ВС, то А → B и A → C. 6. Правило объединения Если А → В и А → С, то А → ВС 7. Правило композиции Если А → B и С → D, то АС → BD 8. Теорема всеобщего объединения Если А→ B и C → D, то А ( С – В ) → BD ● Databases => Normalization 16

Правила вывода ФЗ. Итог ● ● ● Однако, следует иметь в виду, что эти правила не обеспечивают чёткого алгоритма получения всех ФЗ Более того, такого алгоритма не существует Единственный путь – это перебор всех вариантов Databases => Normalization 17

Нормализация ● ● ● Процесс нормализации Понятие функциональных зависимостей Правила вывода ФЗ Декомпозиция без потерь Первая, вторая и третья нормальные формы Нормальная форма Бойса-Кодда Databases => Normalization 18

Декомпозиция без потерь ● ● ● Существенным аспектом процедуры нормализации является декомпозиция – разбиение отношения на производные При этом такое разбиение не должно повлечь за собой потерю информации Если отношение разбито на два без потерь, то это разбиение можно назвать обратимым, т. е. можно произвести обратное соединение Databases => Normalization 19

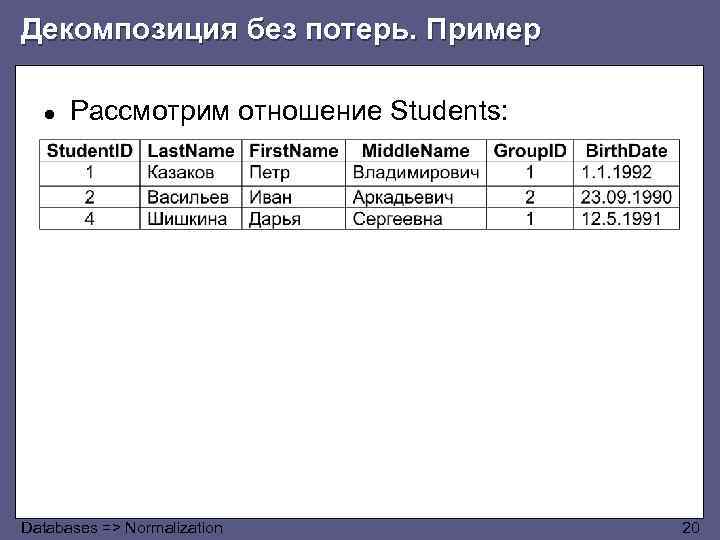Декомпозиция без потерь. Пример ● Рассмотрим отношение Students: Databases => Normalization 20

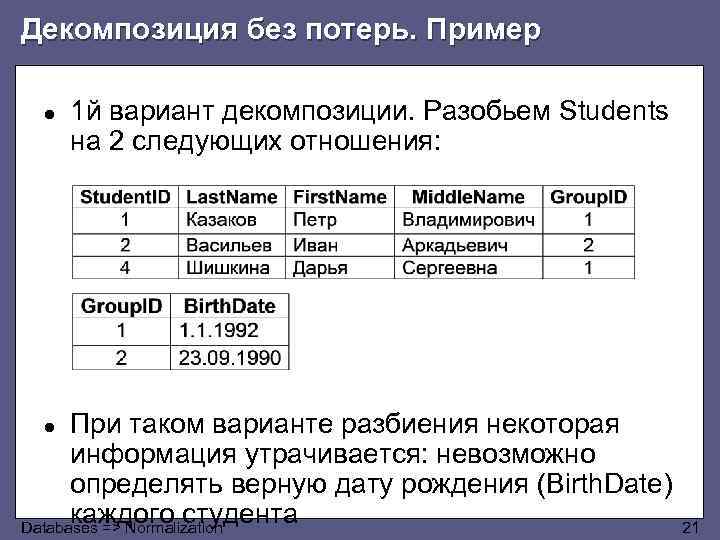Декомпозиция без потерь. Пример ● 1 й вариант декомпозиции. Разобьем Students на 2 следующих отношения: При таком варианте разбиения некоторая информация утрачивается: невозможно определять верную дату рождения (Birth. Date) каждого студента Databases => Normalization 21 ●

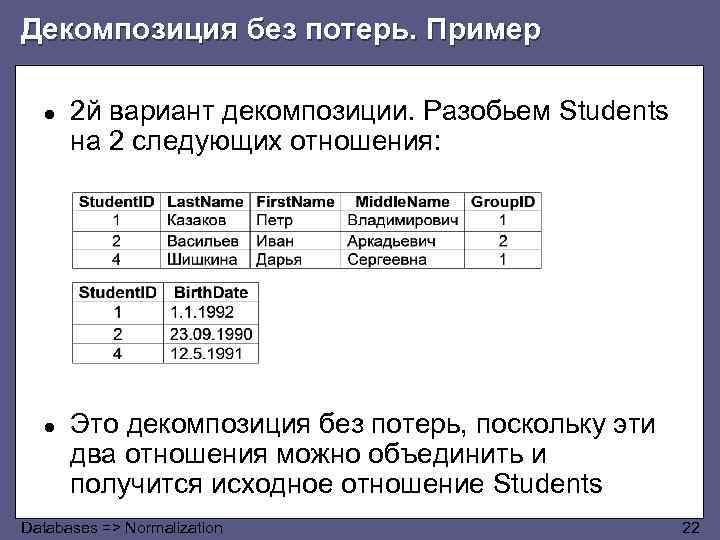Декомпозиция без потерь. Пример ● 2 й вариант декомпозиции. Разобьем Students на 2 следующих отношения: ● Это декомпозиция без потерь, поскольку эти два отношения можно объединить и получится исходное отношение Students Databases => Normalization 22

Декомпозиция без потерь ● ● Можно заметить, что процесс декомпозиции фактически представляет собой операции проекции, т. к. каждое полученное при декомпозиции отношение состоит из подмножества полей исходного отношения Чтобы гарантировать, что после декомпозиции обратное соединение отношений даст исходное, воспользуемся теоремой Хита Databases => Normalization 23

Теорема Хита ● ● Пусть R{А, B, С} – это отношение, где А, B и C – множества атрибутов этого отношения Если R удовлетворяет ФЗ А→ B, то R равна соединению ее проекций по атрибутам {А, В} и {А, С} Databases => Normalization 24

Нормализация ● ● ● Процесс нормализации Понятие функциональных зависимостей Правила вывода ФЗ Декомпозиция без потерь Первая, вторая и третья нормальные формы Нормальная форма Бойса-Кодда Databases => Normalization 25

Первая нормальная форма (1 НФ). Определение ● Отношение находится в 1 НФ тогда и только тогда, когда все используемые домены содержат только скалярные значения, т. е. значения всех полей отношения должны быть неделимы Databases => Normalization 26

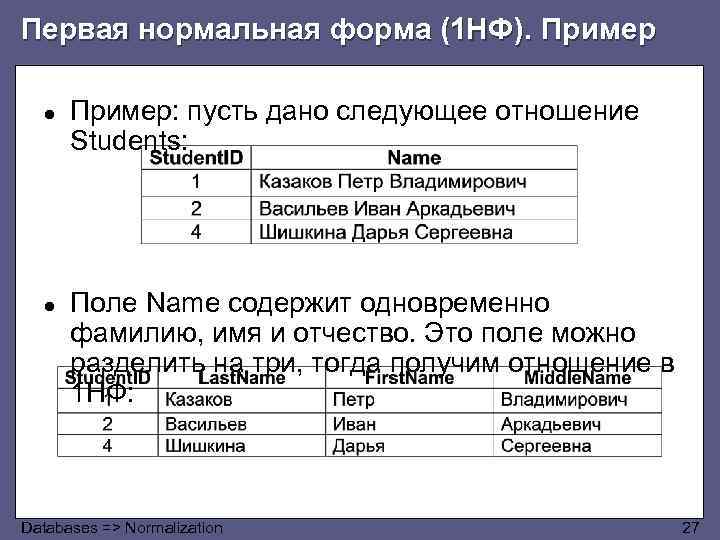Первая нормальная форма (1 НФ). Пример ● Пример: пусть дано следующее отношение Students: ● Поле Name содержит одновременно фамилию, имя и отчество. Это поле можно разделить на три, тогда получим отношение в 1 НФ: Databases => Normalization 27

Вторая нормальная форма (2 НФ). Определение ● Отношение находится во 2 НФ тогда и только тогда, когда оно находится в 1 НФ и каждый неключевой атрибут неприводимо зависит от первичного ключа Databases => Normalization 28

Вторая нормальная форма (2 НФ). Пример ● Рассмотрим следующее отношение: ● Первичным ключом здесь будет: {Student. ID, Course} Проанализируем ФЗ этого отношения, где детерминантом является первичный ключ, а в правой части неключевой атрибут ● Databases => Normalization 29

Вторая нормальная форма (2 НФ). Пример ● ● Продолжение примера: рассмотрим следующую ФЗ: {Student. ID, Course} → {Last. Name} Очевидно, что она является приводимой, т. к. фамилия зависит только от Student. ID, а значит существует ФЗ: {Student. ID} → {Last. Name} Databases => Normalization 30

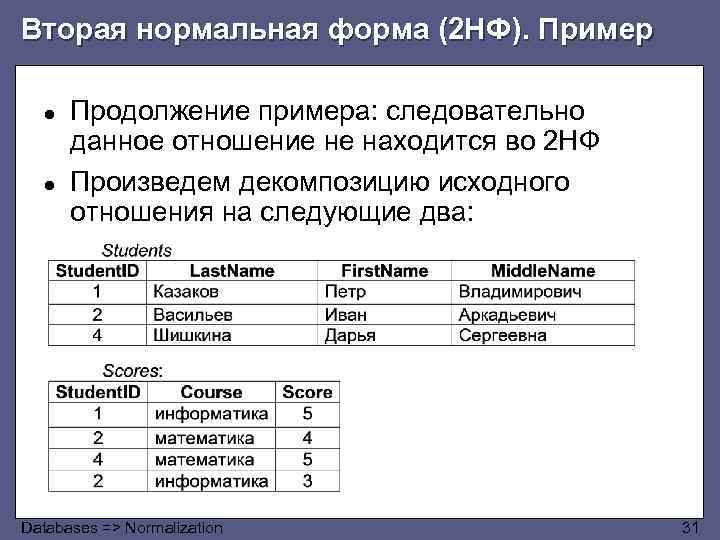Вторая нормальная форма (2 НФ). Пример ● ● Продолжение примера: следовательно данное отношение не находится во 2 НФ Произведем декомпозицию исходного отношения на следующие два: Databases => Normalization 31

Третья нормальная форма (3 НФ). Определение ● Отношение находится в 3 НФ тогда и только тогда, когда оно находится во 2 НФ и каждый неключевой атрибут не является транзитивно зависимым от первичного ключа (это означает, что в отношении отсутствуют какиелибо взаимные зависимости) Databases => Normalization 32

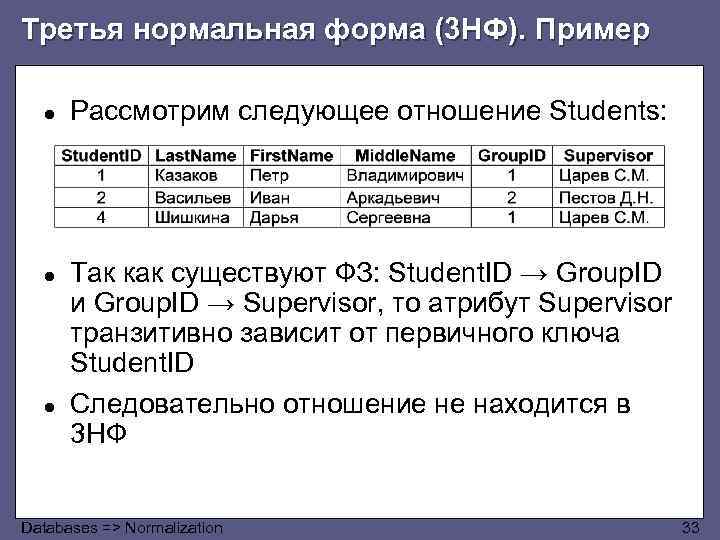Третья нормальная форма (3 НФ). Пример ● Рассмотрим следующее отношение Students: ● Так как существуют ФЗ: Student. ID → Group. ID и Group. ID → Supervisor, то атрибут Supervisor транзитивно зависит от первичного ключа Student. ID Следовательно отношение не находится в 3 НФ ● Databases => Normalization 33

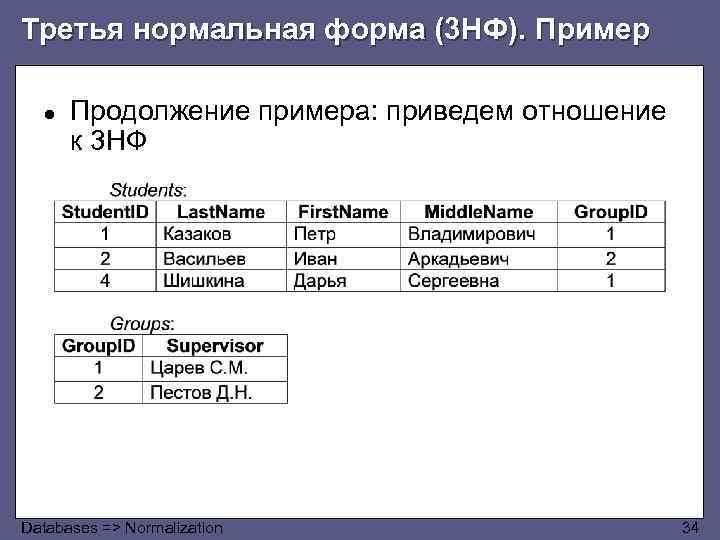Третья нормальная форма (3 НФ). Пример ● Продолжение примера: приведем отношение к 3 НФ Databases => Normalization 34

Нормализация ● ● ● Процесс нормализации Понятие функциональных зависимостей Правила вывода ФЗ Декомпозиция без потерь Первая, вторая и третья нормальные формы Нормальная форма Бойса-Кодда Databases => Normalization 35

Нормальная форма Бойса-Кодда ● ● Нормальная форма Бойса-Кодда (НФБК) – это уточнение третьей нормальной формы При определении 3 НФ было сделано допущение о том, что отношение имеет только один потенциальный ключ, который и является первичным Databases => Normalization 36

Нормальная форма Бойса-Кодда ● В более общем случае первоначальное определение, данное Э. Коддом для ЗНФ, оказывается не во всех случаях удовлетворительным. В частности, оно неадекватно при выполнении следующих условий: o o o отношение имеет два (или больше) потенциальных ключа эти потенциальные ключи являются составными они перекрываются (т. е. имеют по крайней мере один общий атрибут) Поэтому позже исходное определение ЗНФ было заменено более строгим определением Бойса-Кодда Databases => Normalization 37 ●

Нормальная форма Бойса-Кодда. Определение ● Отношение находится в нормальной форме Бойса-Кодда тогда и только тогда, когда каждая ее нетривиальная и неприводимая слева функциональная зависимость имеет в качестве своего детерминанта некоторый потенциальный ключ Databases => Normalization 38

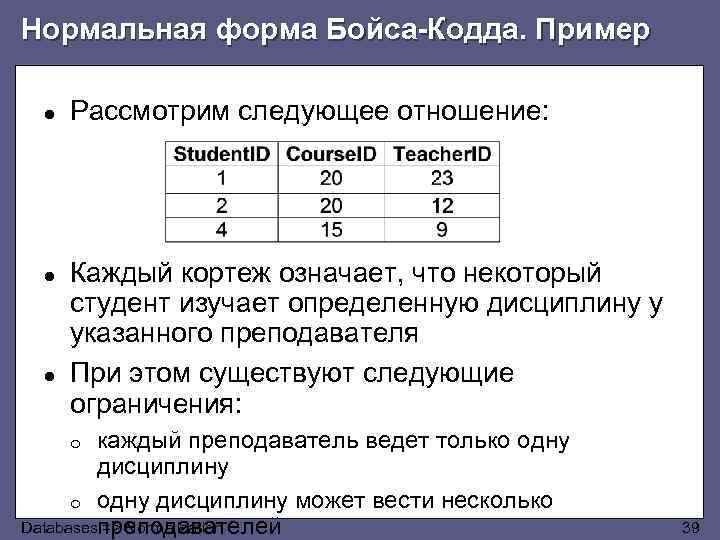Нормальная форма Бойса-Кодда. Пример ● Рассмотрим следующее отношение: ● Каждый кортеж означает, что некоторый студент изучает определенную дисциплину у указанного преподавателя При этом существуют следующие ограничения: ● каждый преподаватель ведет только одну дисциплину o одну дисциплину может вести несколько Databases => Normalization преподавателей o 39

Нормальная форма Бойса-Кодда. Пример ● ● ● Продолжение примера: в данном отношении есть два потенциальных ключа {Student. ID, Course. ID} и {Student. ID, Teacher. ID} Оба ключа являются составными и они имеют общий атрибут Student. ID, т. е. перекрываются Таким образом выполнены все три условия, которые могут привести к ситуации, когда отношение может находиться в 3 НФ, но не находится в НФБК Databases => Normalization 40

Нормальная форма Бойса-Кодда. Пример ● Продолжение примера: очевидно, что отношение находится в 3 НФ: o o o ● значения всех атрибутов неделимы (1 НФ) каждый неключевой атрибут неприводимо зависит от первичного ключа (2 НФ) все неключевые атрибуты нетранзитивно зависят от потенциального ключа (3 НФ) Однако, в данном отношении существует ФЗ Teacher. ID → Course. ID и Teacher. ID при этом не является потенциальным ключом, следовательно отношение не находится в НФБК Databases => Normalization 41

Нормальная форма Бойса-Кодда. Пример Продолжение примера: если произвести декомпозицию этого отношения на два: {Student. ID, Course. ID} и {Course. ID, Teacher. ID}, то потеряем информацию о том, какой именно преподаватель ведет дисциплину для конкретного студента ● Это объясняется тем, что исходное отношение является атомарным, т. е. его нельзя разбить на две независимые проекции ● Таким образом, в процессе нормализации не всегда есть смысл стремиться к атомарным отношениям, но, тем не менее, для основных объектов базы данных рекомендуется Databases => Normalization 42 добиваться атомарности ●

Нормальная форма Бойса-Кодда ● ● ● Если отношение находится только в 1 НФ, но не находится во 2 НФ и 3 НФ, то можно говорить об избыточности информации Избыточность не только увеличивает объём и трудоёмкость заполнения базы данных, но и может привести к аномалиям обновления Аномалии могут приводить к трудностям при вставке, обновлении и удалении, а главное к искажению или потере информации Databases => Normalization 43