DNA Chips and Their Analysis Comp Genomics Lecture

DNA Chips and Their Analysis Comp. Genomics: Lecture 13 based on many sources, primarily Zohar Yakhini

DNA Microarras: Basics • • What are they. Types of arrays (c. DNA arrays, oligo arrays). What is measured using DNA microarrays. How are the measurements done?

DNA Microarras: Computational Questions • • • Design of arrays. Techniques for analyzing experiments. Detecting differential expression. Similar expression: Clustering. Other analysis techniques (mmmmmany). Machine learning techniques, and applications for advanced diagnosis.

What is a DNA Microarray (I) • A surface (nylon, glass, or plastic). • Containing hundreds to thousand pixels. • Each pixel has copies of a sequence of single stranded DNA (ss. DNA). • Each such sequence is called a probe.

What is a DNA Microarray (II) • An experiment with 500 -10 k elements. • Way to concurrently explore the function of multiple genes. • A snapshot of the expression level of 500 -10 k genes under given test conditions

Some Microarray Terminology • Probe: ss. DNA printed on the solid substrate (nylon or glass). These are short substrings of the genes we are going to be testing • Target: c. DNA which has been labeled and is to be washed over the probe

Back to Basics: Watson and Crick James Watson and Francis Crick discovered, in 1953, the double helix structure of DNA. From Zohar Yakhini

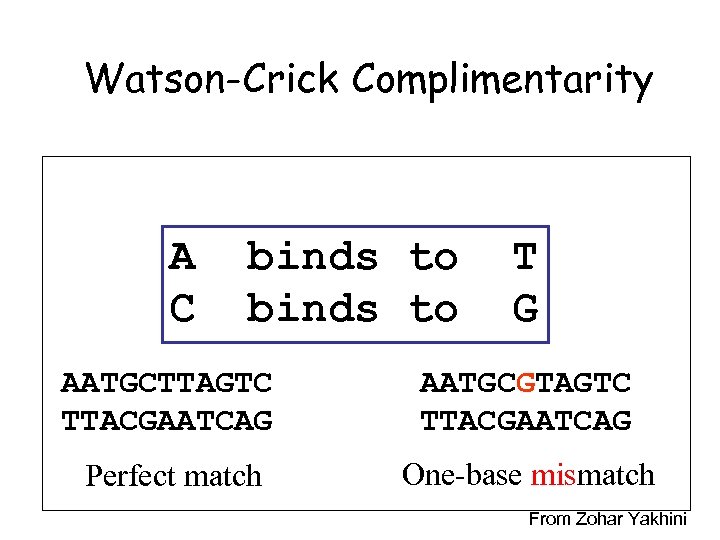Watson-Crick Complimentarity A C binds to T G AATGCTTAGTC TTACGAATCAG AATGCGTAGTC TTACGAATCAG Perfect match One-base mismatch From Zohar Yakhini

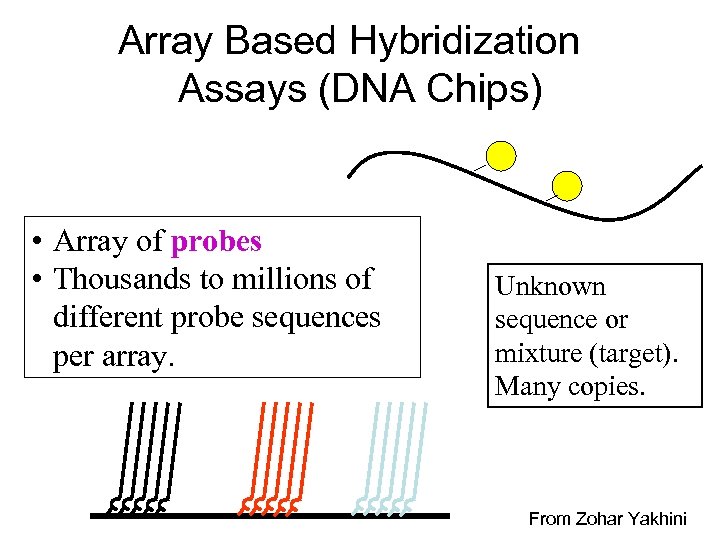Array Based Hybridization Assays (DNA Chips) • Array of probes • Thousands to millions of different probe sequences per array. Unknown sequence or mixture (target). Many copies. From Zohar Yakhini

Array Based Hyb Assays • Target hybs to WC complimentary probes only • Therefore – the fluorescence pattern is indicative of the target sequence. From Zohar Yakhini

DNA Sequencing Sanger Method • Generate all A, C, G, T – terminated prefixes of the sequence, by a polymerase reaction with terminating corresponding bases. • Run in four different gel lanes. • Reconstruct sequence from the information on the lengths of all A, C, G, T – terminated prefixes. • The need for 4 different reactions is avoided by using differentially dye labeled terminating bases. From Zohar Yakhini

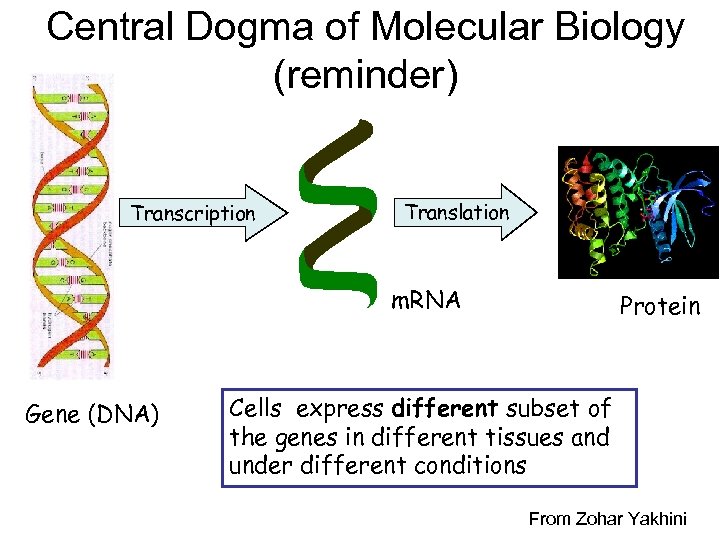Central Dogma of Molecular Biology (reminder) Transcription Translation m. RNA Gene (DNA) Protein Cells express different subset of the genes in different tissues and under different conditions From Zohar Yakhini

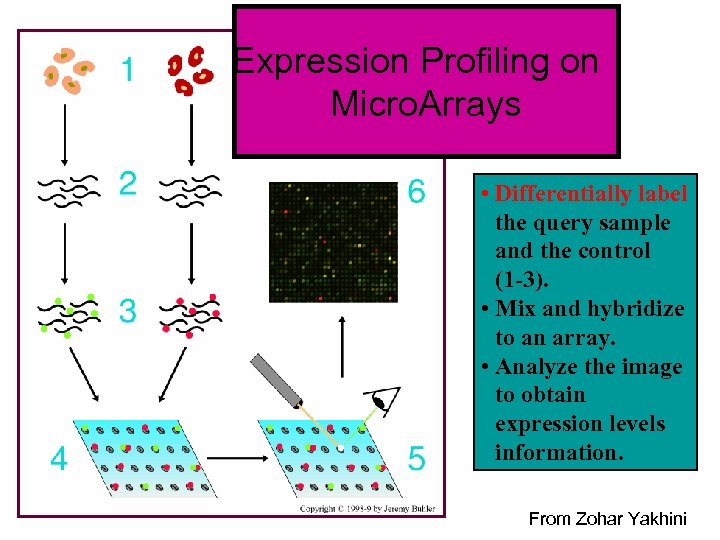
Expression Profiling on Micro. Arrays • Differentially label the query sample and the control (1 -3). • Mix and hybridize to an array. • Analyze the image to obtain expression levels information. From Zohar Yakhini

Microarray: 2 Types of Fabrication 1. c. DNA Arrays: Deposition of DNA fragments – Deposition of PCR-amplified c. DNA clones – Printing of already synthesized oligonucleotieds 2. Oligo Arrays: In Situ synthesis – Photolithography – Ink Jet Printing – Electrochemical Synthesis By Steve Hookway lecture and Sorin Draghici’s book “Data Analysis Tools for DNA Microarrays”

c. DNA Microarrays vs. Oligonucleotide Probes and Cost c. DNA Arrays • Long Sequences • Spot Unknown Sequences • More variability • Arrays cheaper Oligonucleotide Arrays • Short Sequences • Spot Known Sequences • More reliable data • Arrays typically more expensive By Steve Hookway lecture and Sorin Draghici’s book “Data Analysis Tools for DNA Microarrays”

Photolithography (Affymetrix) • Similar to process used to generate VLSI circuits • Photolithographic masks are used to add each base • If base is present, there will be a “hole” in the corresponding mask • Can create high density arrays, but sequence length is limited Photodeprotection mask C From “Data Analysis Tools for DNA Microarrays” by Sorin Draghici

Photolithography (Affymetrix) From Zohar Yakhini

Ink Jet Printing • Four cartridges are loaded with the four nucleotides: A, G, C, T • As the printer head moves across the array, the nucleotides are deposited in pixels where they are needed. • This way (many copies of) a 20 -60 base long oligo is deposited in each pixel. By Steve Hookway lecture and Sorin Draghici’s book “Data Analysis Tools for DNA Microarrays”

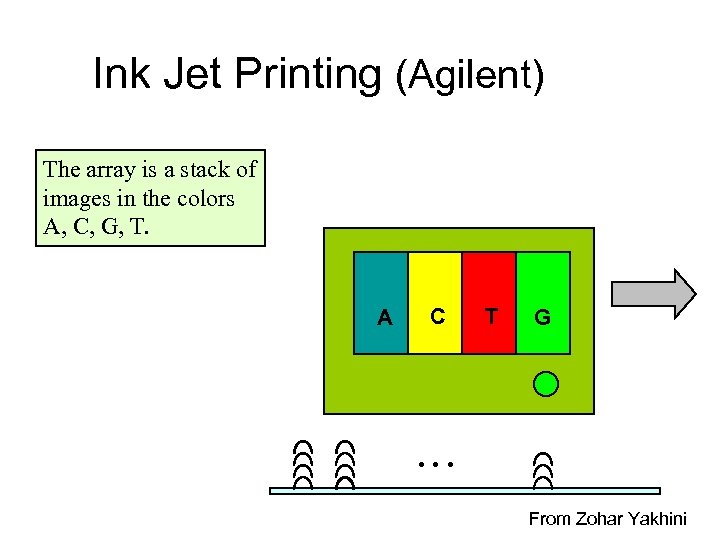Ink Jet Printing (Agilent) The array is a stack of images in the colors A, C, G, T. A C T G … From Zohar Yakhini

Inkjet Printed Microarrays Inkjet head, squirting phosphor-ammodites From Zohar Yakhini

Electrochemical Synthesis • Electrodes are embedded in the substrate to manage individual reaction sites • Electrodes are activated in necessary positions in a predetermined sequence that allows the sequences to be constructed base by base • Solutions containing specific bases are washed over the substrate while the electrodes are activated From “Data Analysis Tools for DNA Microarrays” by Sorin Draghici

Preparation of Samples • Use oligo(d. T) on a separation column to extract m. RNA from total cell populations. • Use olig(d. T) initiated polymerase to reverse transcribe RNA into fluorescence labeled c. DNA. RNA is unstable because of environment RNAdigesting enzymes. • Alternatively – use random priming for this purpose, generating a population of transcript subsequences From Zohar Yakhini

Expression Profiling on Micro. Arrays • Differentially label the query sample and the control (1 -3). • Mix and hybridize to an array. • Analyze the image to obtain expression levels information. From Zohar Yakhini

Expression Profiling: a FLASH Demo URL: http: //www. bio. davidson. edu/courses/genomics/chip. html

Expression Profiling – Probe Design Issues • Probe specificity and sensitivity. • Special designs for splice variations or other custom purposes. • Flat thermodynamics. • Generic and universal systems From Zohar Yakhini

Hybridization Probes • Sensitivity: Strong interaction between the probe and its intended target, under the assay's conditions. How much target is needed for the reaction to be detectable or quantifiable? • Specificity: No potential cross hybridization. From Zohar Yakhini

Specificity • Symbolic specificity • Statistical protection in the unknown part of the genome. Methods, software and application in collaboration with Peter Webb, Doron Lipson. From Zohar Yakhini

Reading Results: Color Coding Campbell & Heyer, 2003 • Numeric tables are difficult to read • Data is presented with a color scale • Coding scheme: – Green = repressed (less m. RNA) gene in experiment – Red = induced (more m. RNA) gene in experiment – Black = no change (1: 1 ratio) • Or – Green = control condition (e. g. aerobic) – Red = experimental condition (e. g. anaerobic) • We usually use ratio

Thermal Ink Jet Arrays, by Agilent Technologies In-Situ synthesized oligonucleotide array. 25 -60 mers. c. DNA array, Inkjet deposition

Application of Microarrays • We only know the function of about 30% of the 30, 000 genes in the Human Genome – Gene exploration – Functional Genomics • First among many high throughput genomic devices http: //www. gene-chips. com/sample 1. html By Steve Hookway lecture and Sorin Draghici’s book “Data Analysis Tools for DNA Microarrays”

A Data Mining Problem • On a given microarray, we test on the order of 10 k elements in one time • Number of microarrays used in typical experiment is no more than 100. • Insufficient sampling. • Data is obtained faster than it can be processed. • High noise. • Algorithmic approaches to work through this large data set and make sense of the data are desired.

Informative Genes in a Two Classes Experiment • Differentially expressed in the two classes. • Identifying (statistically significant) informative genes - Provides biological insight - Indicate promising research directions - Reduce data dimensionality - Diagnostic assay From Zohar Yakhini

Scoring Genes Expression pattern and pathological diagnosis information (annotation), for a single gene + a 1 + a 2 a 3 a 4 + a 5 + a 6 + a 7 a 8 a 9 + + + a 10 a 11 a 12 a 13 a 14 a 15 Permute the annotation by sorting the expression pattern (ascending, say). Informative genes Non-informative genes + + + + - - - - + + + + - - + + + + - - - + + - - + + - + - etc From Zohar Yakhini

Threshold Error Rate (TNo. M) Score Find the threshold that best separates tumors from normals, count the number of errors committed there. Ex 1: - + + - - + 6 7 # of errors = min(7, 8) = 7. Ex 2: A perfect single gene classifier gets a score of 0. + + + + - - - - 0 From Zohar Yakhini

p-Values • Relevance scores are more useful when we can compute their significance: – p-value: The probability of finding a gene with a given score if the labeling is random • p-Values allow for higher level statistical assessment of data quality. • p-Values provide a uniform platform for comparing relevance, across data sets. • p-Values enable class discovery From Zohar Yakhini

BRCA 1 Differential Expression Genes over-expressed in BRCA 1 wildtype Genes over-expressed in BRCA 1 mutants Collab with NIH NEJM 2001 Sporadic sample s 14321 With BRCA 1 -mutant expression profile BRCA 1 mutants BRCA 1 Wildtype From Zohar Yakhini

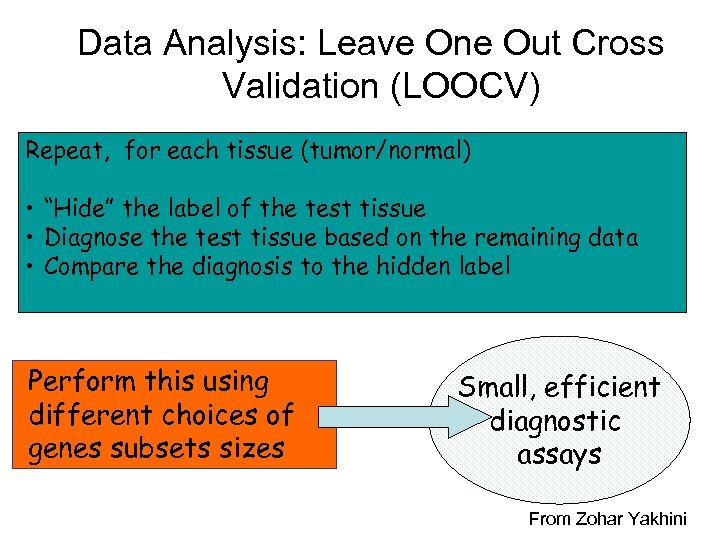Data Analysis: Leave One Out Cross Validation (LOOCV) Repeat, for each tissue (tumor/normal) • “Hide” the label of the test tissue • Diagnose the test tissue based on the remaining data • Compare the diagnosis to the hidden label Perform this using different choices of genes subsets sizes Small, efficient diagnostic assays From Zohar Yakhini

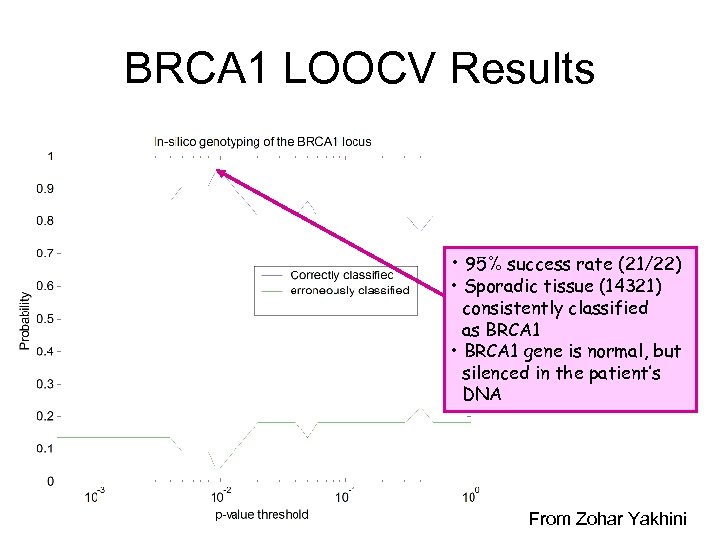BRCA 1 LOOCV Results • 95% success rate (21/22) • Sporadic tissue (14321) consistently classified as BRCA 1 • BRCA 1 gene is normal, but silenced in the patient’s DNA From Zohar Yakhini

Lung Cancer Informative Genes Data from Naftali Kaminski’s lab, at Sheba. • 24 tumors (various types and origins) • 10 normals (normal edges and normal lung pools) From Zohar Yakhini

And Now: Global Analysis of Gene Expression Data First (but not least): Clustering either of genes, or of experiments

Example data: fold change (ratios) Name 0 hours 2 hours 4 hours 6 hours 8 hours 10 hours Gene C 1 8 12 16 12 8 Gene D 1 3 4 4 3 2 Gene E 1 4 8 8 Gene F 1 1 1 0. 25 0. 1 Gene G 1 2 3 4 3 2 Gene H 1 0. 5 0. 33 0. 25 0. 33 0. 5 Gene I 1 4 8 4 1 0. 5 Gene J 1 2 1 2 Gene K 1 1 3 3 Gene L 1 2 3 4 3 2 Gene M 1 0. 33 0. 25 0. 33 Campbell & Heyer, 2003 Gene N 1 0. 125 0. 0833 0. 0625 0. 0833 0. 125 0. 5

Example data 2 Name 0 hours 2 hours 4 hours 6 hours 8 hours 10 hours Gene C 0 3 3. 58 4 3. 58 3 Gene D 0 1. 58 2 2 1. 58 1 Gene E 0 2 3 3 Gene F 0 0 0 -2 -2 -3. 32 Gene G 0 1 1. 58 2 1. 58 1 Gene H 0 -1 -1. 60 -2 -1. 60 -1 Gene I 0 2 3 2 0 -1 Gene J 0 1 0 1 Gene K 0 0 1. 58 Gene L 0 1 1. 58 2 1. 58 1 Gene M 0 -1. 60 -2 -2 -1. 60 Campbell & Heyer, 2003 Gene N 0 -3 -3. 59 -4 -3. 59 -3 -1

Pearson Correlation Coefficient, r. values in [-1, 1] interval • Gene expression over d experiments is a vector in Rd, e. g. for gene C: (0, 3, 3. 58, 4, 3. 58, 3) • Given two vectors X and Y that contain N elements, we calculate r as follows: Cho & Won, 2003

Example: Pearson Correlation Coefficient, r • X = Gene C = (0, 3. 00, 3. 58, 4, 3. 58, 3) Y = Gene D = (0, 1. 58, 2. 00, 2, 1. 58, 1) • ∑XY = (0)(0)+(3)(1. 58)+(3. 58)(2)+(4)(2)+(3. 58)(1. 58)+(3)(1) = 28. 5564 • ∑X = 3+3. 58+4+3. 58+3 = 17. 16 • ∑X 2 = 32+3. 582+42+3. 582+32 = 59. 6328 • ∑Y = 1. 58+2+2+1. 58+1 = 8. 16 • ∑Y 2 = 1. 582+22+22+1. 582+12 = 13. 9928 • N=6 • ∑XY – ∑X∑Y/N = 28. 5564 – (17. 16)(8. 16)/6 = 5. 2188 • ∑X 2 – (∑X)2/N = 59. 6328 – (17. 16)2/6 = 10. 5552 • ∑Y 2 – (∑Y)2/N = 13. 9928 – (8. 16)2/6 = 2. 8952 • r = 5. 2188 / sqrt((10. 5552)(2. 8952)) = 0. 944

Example data: Pearson correlation coefficients Gene C Gene D Gene E Gene F Gene G Gene H Gene I Gene J Gene K Gene L Gene M Gene N Gene C 1 0. 94 0. 96 -0. 40 0. 95 -0. 95 0. 41 0. 36 0. 23 0. 95 -0. 94 -1 Gene D 0. 94 1 0. 84 -0. 10 0. 94 -0. 94 0. 68 0. 24 -0. 07 0. 94 -1 -0. 94 Gene E 0. 96 0. 84 1 -0. 57 0. 89 -0. 89 0. 21 0. 30 0. 43 0. 89 -0. 84 -0. 96 Gene F -0. 40 -0. 10 -0. 57 1 -0. 35 0. 60 -0. 43 -0. 79 -0. 35 0. 10 0. 40 Gene G 0. 95 0. 94 0. 89 -0. 35 1 -1 0. 48 0. 22 0. 11 1 -0. 94 -0. 95 Gene H -0. 95 -0. 94 -0. 89 0. 35 -1 1 -0. 48 -0. 21 -0. 11 -1 0. 94 0. 95 Gene I 0. 41 0. 68 0. 21 0. 60 0. 48 -0. 48 1 0 -0. 75 0. 48 -0. 68 -0. 41 Gene J 0. 36 0. 24 0. 30 -0. 43 0. 22 -0. 21 0 0. 22 -0. 24 -0. 36 Gene K 0. 23 -0. 07 0. 43 -0. 79 0. 11 -0. 75 0 1 0. 11 0. 07 -0. 23 Gene L 0. 95 0. 94 0. 89 -0. 35 1 -1 0. 48 0. 22 0. 11 1 -0. 94 -0. 95 Gene M -0. 94 -1 -0. 84 0. 10 -0. 94 -0. 68 -0. 24 0. 07 -0. 94 1 0. 94 Gene N -1 -0. 94 -0. 96 0. 40 -0. 95 -0. 41 -0. 36 -0. 23 -0. 95 Campbell & Heyer, 2003 0. 94 1

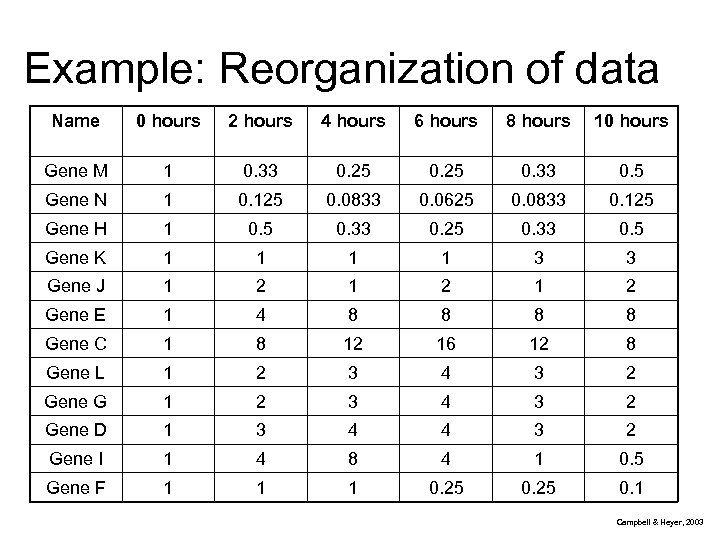Example: Reorganization of data Name 0 hours 2 hours 4 hours 6 hours 8 hours 10 hours Gene M 1 0. 33 0. 25 0. 33 0. 5 Gene N 1 0. 125 0. 0833 0. 0625 0. 0833 0. 125 Gene H 1 0. 5 0. 33 0. 25 0. 33 0. 5 Gene K 1 1 3 3 Gene J 1 2 1 2 Gene E 1 4 8 8 Gene C 1 8 12 16 12 8 Gene L 1 2 3 4 3 2 Gene G 1 2 3 4 3 2 Gene D 1 3 4 4 3 2 Gene I 1 4 8 4 1 0. 5 Gene F 1 1 1 0. 25 0. 1 Campbell & Heyer, 2003

Spearman Rank Order Coefficient • Replace each entry xi by its rank in vector x. • Then compute Pearson correlation coefficients of rank vectors. • Example: X = Gene C = (0, 3. 00, 3. 41, 4, 3. 58, 3. 01) Y = Gene D = (0, 1. 51, 2. 00, 2. 32, 1. 58, 1) • Ranks(X)= (1, 2, 4, 6, 5, 3) • Ranks(Y)= (1, 3, 5, 6, 4, 2) • Ties should be taken care of: (1) rare (2) randomize (small effect)

Grouping and Reduction • Grouping: Partition items into groups. Items in same group should be similar. Items in different groups should be dissimilar. • Grouping may help discover patterns in the data. • Reduction: reduce the complexity of data by removing redundant probes (genes).

Unsupervised Grouping: Clustering • Pattern discovery via clustering similarly expressed genes together • Techniques most often used: k-Means Clustering n Hierarchical Clustering n Biclustering n Alternative Methods: Self Organizing Maps (SOMS), plaid models, singular value decomposition (SVD), order preserving submatrices (OPSM), …… n

Clustering Overview • Different similarity measures in use: – – – – – Pearson Correlation Coefficient Cosine Coefficient Euclidean Distance Information Gain Mutual Information Signal to noise ratio Simple Matching for Nominal

Clustering Overview (cont. ) • Different Clustering Methods – Unsupervised • k-means Clustering (k nearest neighbors) • Hierarchical Clustering • Self-organizing map – Supervised • Support vector machine • Ensemble classifier ðData Mining

Clustering Limitations • Any data can be clustered, therefore we must be careful what conclusions we draw from our results • Clustering is often randomized and can and will produce different results for different runs on same data

K-means Clustering • Given a set of m data points in n-dimensional space and an integer k. • We want to find the set of k “centers” in n-dimensional space that minimizes the Euclidean (mean squared) distance from each data point to its nearest center. • No exact polynomial-time algorithms are known for this problem (no wonder, NP-hard!). “A Local Search Approximation Algorithm for k-Means Clustering” by Kanungo et. al

K-means Heuristic (Lloyd’s Algorithm) • Has been shown to converge to a locally optimal solution • But can converge to a solution arbitrarily bad compared to the optimal solution Data Points Optimal Centers Heuristic Centers K=3 • “K-means-type algorithms: A generalized convergence theorem and characterization of local optimality” by Selim and Ismail • “A Local Search Approximation Algorithm for k-Means Clustering” by Kanungo et al.

Euclidean Distance Now to find the distance between two points, say the origin and the point (3, 4): Simple and Fast! Remember this when we consider the complexity!

Finding a Centroid We use the following equation to find the n dimensional centroid point (center of mass) amid k (n dimensional) points: Example: Let’s find the midpoint between three 2 D points, say: (2, 4) (5, 2) (8, 9)

K-means Iterative Heuristic • • • Choose k initial center points “randomly” Cluster data using Euclidean distance (or other distance metric) Calculate new center points for each cluster, using only points within the cluster Re-Cluster all data using the new center points (this step could cause some data points to be placed in a different cluster) Repeat steps 3 & 4 until no data points are moved from one cluster to another (stabilization), or till some other convergence criteria is met From “Data Analysis Tools for DNA Microarrays” by Sorin Draghici

An example with 2 clusters 1. We Pick 2 centers at random 2. We cluster our data around these center points Figure Reproduced From “Data Analysis Tools for DNA Microarrays” by Sorin Draghici

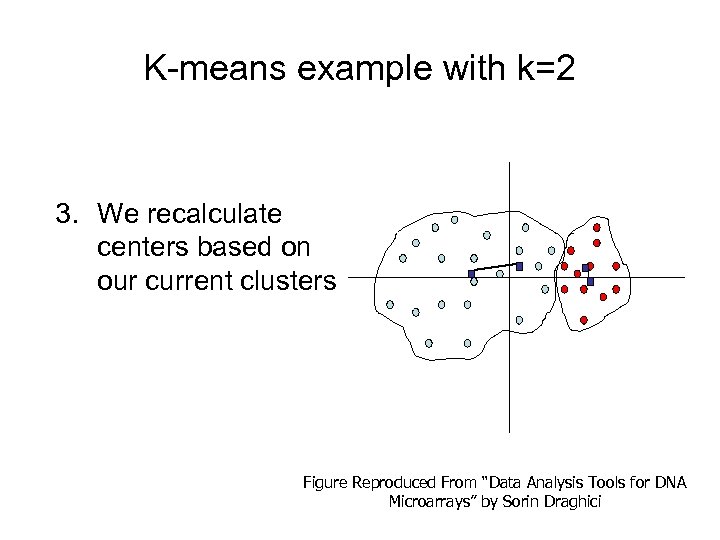K-means example with k=2 3. We recalculate centers based on our current clusters Figure Reproduced From “Data Analysis Tools for DNA Microarrays” by Sorin Draghici

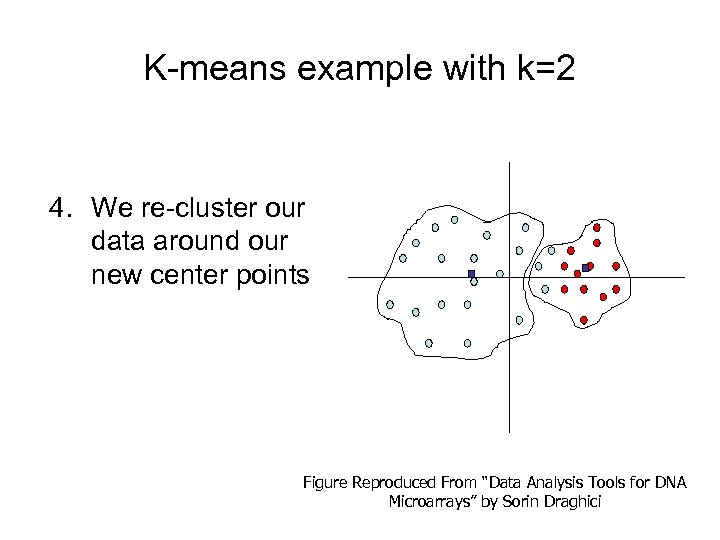K-means example with k=2 4. We re-cluster our data around our new center points Figure Reproduced From “Data Analysis Tools for DNA Microarrays” by Sorin Draghici

K-means example with k=2 5. We repeat the last two steps until no more data points are moved into a different cluster Figure Reproduced From “Data Analysis Tools for DNA Microarrays” by Sorin Draghici

Choosing k • Run algorithm on data with several different values of k • Use advance knowledge about the characteristics of your test (e. g. Cancerous vs Non-Cancerous Tissues, in case the experiments are being clustered)

Cluster Quality • Since any data can be clustered, how do we know our clusters are meaningful? – The size (diameter) of the cluster vs. the inter-cluster distance – Distance between the members of a cluster and the cluster’s center – Diameter of the smallest sphere containing the cluster From “Data Analysis Tools for DNA Microarrays” by Sorin Draghici

Cluster Quality Continued distance=20 diameter=5 distance=5 diameter=5 Quality of cluster assessed by ratio of distance to nearest cluster and cluster diameter Figure Reproduced From “Data Analysis Tools for DNA Microarrays” by Sorin Draghici

Cluster Quality Continued Quality can be assessed simply by looking at the diameter of a cluster (alone? ? ) A cluster can be formed by the heuristic even when there is no similarity between clustered patterns. This occurs because the algorithm forces k clusters to be created. From “Data Analysis Tools for DNA Microarrays” by Sorin Draghici

Characteristics of k-means Clustering • The random selection of initial center points creates the following properties – Non-Determinism – May produce clusters without patterns • One solution is to choose the centers randomly from existing patterns From “Data Analysis Tools for DNA Microarrays” by Sorin Draghici

Heuristic’s Complexity • Linear in the number of data points, N • Can be shown to have run time c. N, where c does not depend on N, but rather the number of clusters, k • (not sure about dependence on dimension, n? ) heuristic is efficient From “Data Analysis Tools for DNA Microarrays” by Sorin Draghici

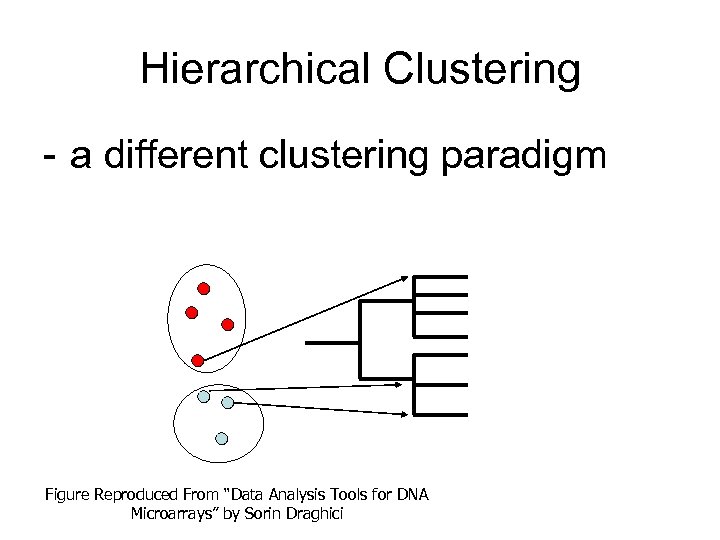Hierarchical Clustering - a different clustering paradigm Figure Reproduced From “Data Analysis Tools for DNA Microarrays” by Sorin Draghici

Hierarchical Clustering (cont. ) Gene C Gene D Gene E Gene F Gene G Gene H Gene I Gene J Gene K Gene L Gene M Gene N 0. 94 0. 96 -0. 40 0. 95 -0. 95 0. 41 0. 36 0. 23 0. 95 -0. 94 -1 0. 84 -0. 10 0. 94 -0. 94 0. 68 0. 24 -0. 07 0. 94 -1 -0. 94 -0. 57 0. 89 -0. 89 0. 21 0. 30 0. 43 0. 89 -0. 84 -0. 96 -0. 35 0. 60 -0. 43 -0. 79 -0. 35 0. 10 0. 40 -1 0. 48 0. 22 0. 11 1 -0. 94 -0. 95 -0. 48 -0. 21 -0. 11 -1 0. 94 0. 95 0 -0. 75 0. 48 -0. 68 -0. 41 0 0. 22 -0. 24 -0. 36 0. 11 0. 07 -0. 23 -0. 94 -0. 95 Campbell & Heyer, 2003 0. 94

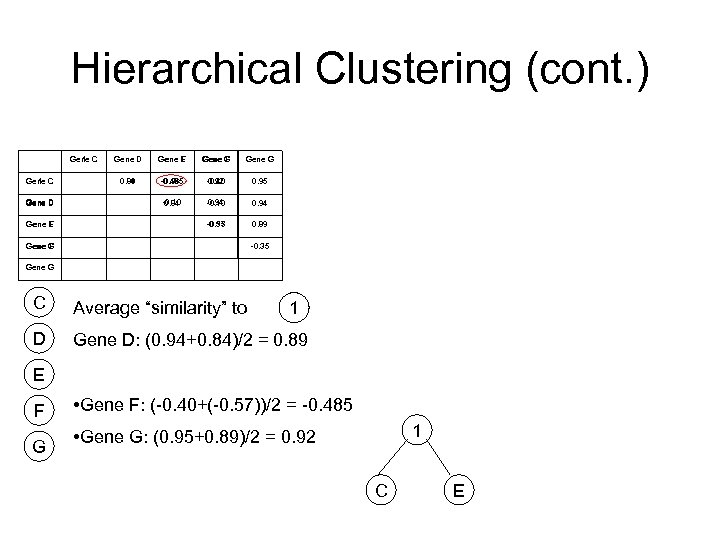Hierarchical Clustering (cont. ) Gene C 1 Gene D F Gene E Gene D Gene E F Gene G Gene F Gene G 0. 89 0. 94 -0. 485 0. 96 -0. 40 0. 92 0. 95 -0. 10 0. 84 0. 94 -0. 10 0. 94 -0. 35 -0. 57 0. 89 Gene G F -0. 35 Gene G C Average “similarity” to D Gene D: (0. 94+0. 84)/2 = 0. 89 1 E F G • Gene F: (-0. 40+(-0. 57))/2 = -0. 485 1 • Gene G: (0. 95+0. 89)/2 = 0. 92 C E

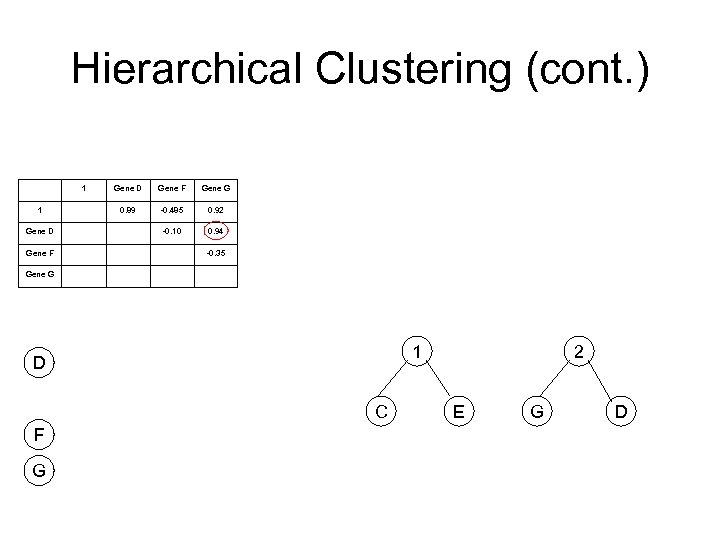Hierarchical Clustering (cont. ) 1 1 Gene D Gene F Gene G 0. 89 -0. 485 0. 92 -0. 10 0. 94 -0. 35 Gene G 1 D C F G 2 E G D

Hierarchical Clustering (cont. ) 1 1 2 2 Gene F 0. 905 -0. 485 -0. 225 3 Gene F 1 C F 2 E G D

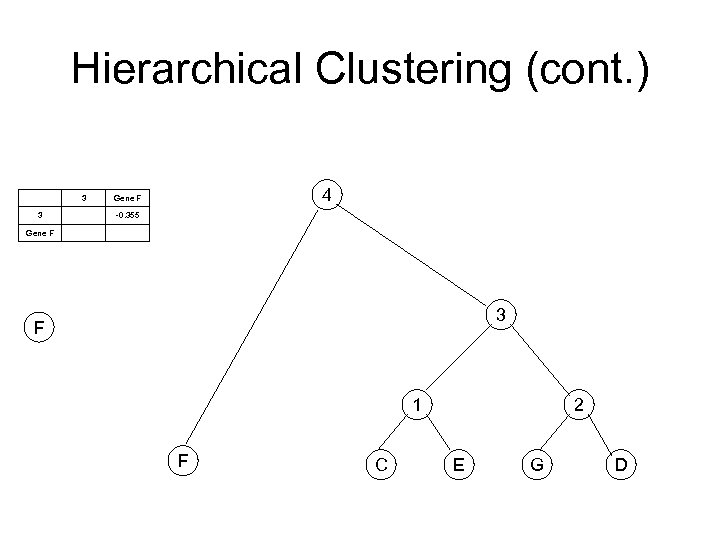Hierarchical Clustering (cont. ) 3 3 4 Gene F -0. 355 Gene F 3 F 1 F C 2 E G D

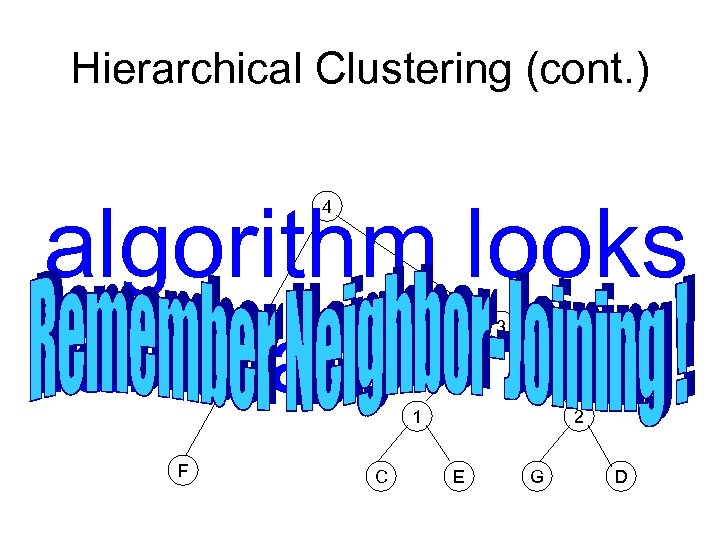Hierarchical Clustering (cont. ) algorithm looks familiar? 4 3 1 F C 2 E G D

Clustering of entire yeast genome Campbell & Heyer, 2003

Hierarchical Clustering: Yeast Gene Expression Data Eisen et al. , 1998

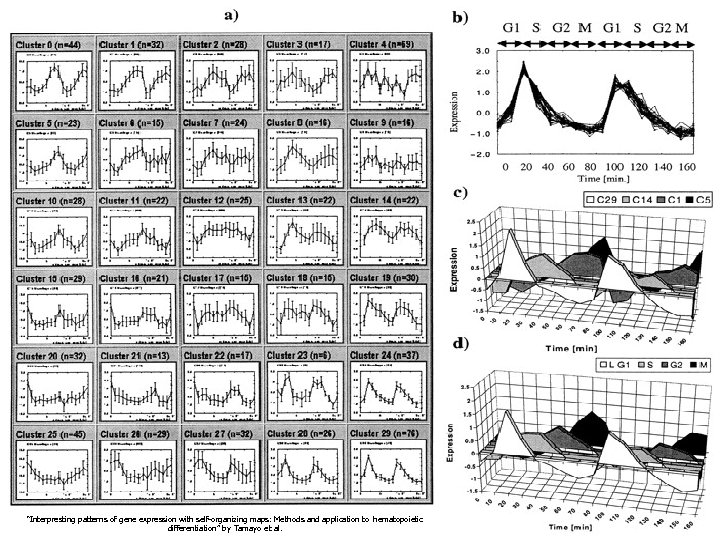A SOFM Example With Yeast “Interpresting patterns of gene expression with self-organizing maps: Methods and application to hematopoietic differentiation” by Tamayo et al.

SOM Description • Each unit of the SOM has a weighted connection to all inputs • As the algorithm progresses, neighboring units are grouped by similarity Output Layer Input Layer From “Data Analysis Tools for DNA Microarrays” by Sorin Draghici

An Example Using Color Each color in the map is associated with a weight From http: //davis. wpi. edu/~matt/courses/soms/

Cluster Analysis of Microarray Expression Data Matrices Application of cluster analysis techniques in the elucidation gene expression data

Function of Genes The features of a living organism are governed principally by its genes. If we want to fully understand living systems we must know the function of each gene. Once we know a gene’s sequence we can design experiments to find its function: The Classical Approach of Assigning a function to a Gene )"זבוב בלי רגליים (" – חרש Delete Gene X Conclusion: Gene X = left eye gene. However this approach is too slow to handle all the gene sequence information we have today (HGSP).

Microarray Analysis Microarray analysis allows the monitoring of the activities of many genes over many different conditions. Experiments are carried out on a Physical Matrix like the one below: Low Zero High C 1 C 2 C 3 C 4 C 5 C 6 C 7 G 1 G 2 G 3 G 4 G 5 G 6 G 7 Possible inference: Conditions 1. 55 1. 05 0. 5 2. 5 1. 75 0. 25 0. 1 1. 7 0. 3 2. 4 2. 9 1. 5 0. 5 1. 0 1. 55 1. 05 0. 5 2. 5 1. 75 0. 25 0. 1 1. 7 Genes 0. 3 2. 4 1. 5 0. 5 1. 0 1. 55 2. 5 1. 75 0. 25 0. 1 0. 3 1. 55 0. 5 2. 4 2. 9 1. 5 0. 5 1. 05 0. 5 2. 5 1. 75 0. 25 0. 1 To facilitate computational analysis the physical matrix which may contain 1000’s of gene’s is converted into a numerical matrix using image analysis equipment. If Gene X’s activity (expression) is affected by Condition Y (Extreme Heat), then Gene X may be involved in protecting the cellular components from extreme heat. Each Gene has its corresponding Expression Profile for a set of conditions. This Expression Profile may be thought of as a feature profile for that gene for that set of conditions (A condition feature profile).

Cluster Analysis • Cluster Analysis is an unsupervised procedure which involves grouping of objects based on their similarity in feature space. • In the Gene Expression context Genes are grouped based on the similarity of their Condition feature profile. • Cluster analysis was first applied to Gene Expression data from Brewer’s Yeast (Saccharomyces cerevisiae) by Eisen et al. (1998). Z Conditions 1. 55 1. 05 0. 5 2. 5 1. 75 0. 25 0. 1 1. 7 0. 3 2. 4 2. 9 1. 5 0. 5 1. 0 1. 55 1. 05 0. 5 2. 5 1. 75 0. 25 0. 1 1. 7 Genes 0. 3 2. 4 1. 5 0. 5 1. 0 1. 55 2. 5 1. 75 0. 25 2. 4 2. 9 1. 5 0. 5 1. 05 0. 5 2. 5 1. 75 0. 25 0. 1 B Y 0. 1 0. 3 1. 55 0. 5 A Clustering C Clusters A, B and C represent groups of related genes. X Two general conclusions can be drawn from these clusters: • Genes clustered together may be related within a biological module/system. • If there are genes of known function within a cluster these may help to class this biological/module system.

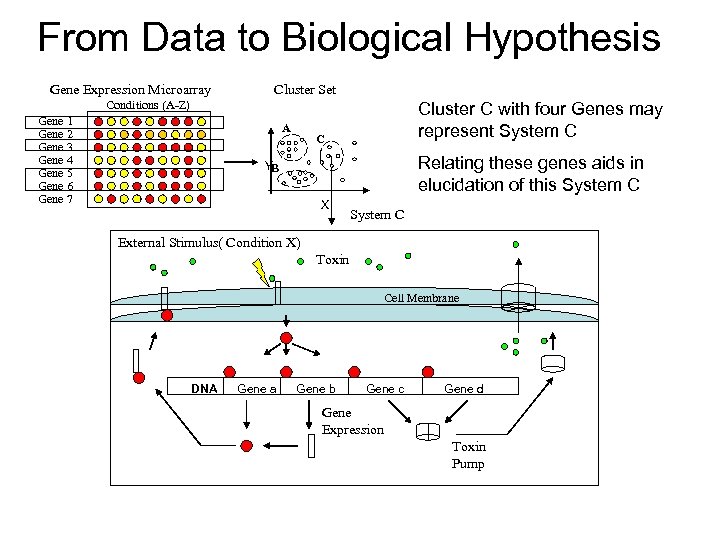From Data to Biological Hypothesis Gene Expression Microarray Cluster Set Conditions (A-Z) Gene 1 Gene 2 Gene 3 Gene 4 Gene 5 Gene 6 Gene 7 A Cluster C with four Genes may represent System C C Relating these genes aids in elucidation of this System C YB X System C External Stimulus( Condition X) Toxin Cell Membrane Regulator Protein DNA Gene a Gene b Gene c Gene d Gene Expression Toxin Pump

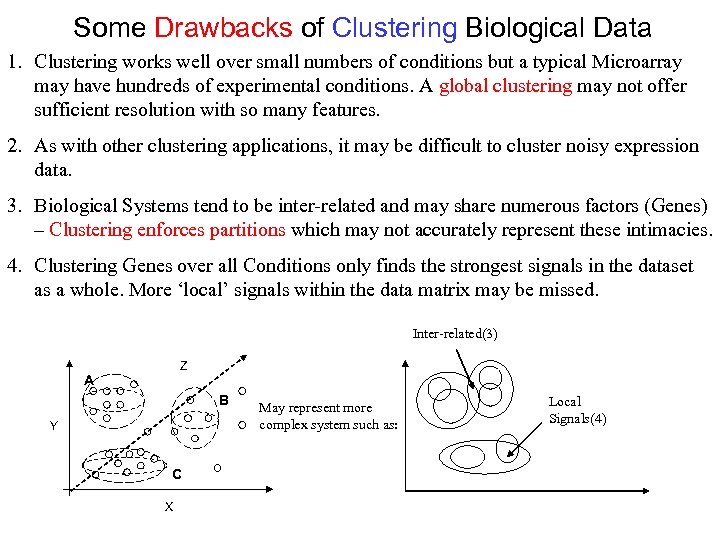Some Drawbacks of Clustering Biological Data 1. Clustering works well over small numbers of conditions but a typical Microarray may have hundreds of experimental conditions. A global clustering may not offer sufficient resolution with so many features. 2. As with other clustering applications, it may be difficult to cluster noisy expression data. 3. Biological Systems tend to be inter-related and may share numerous factors (Genes) – Clustering enforces partitions which may not accurately represent these intimacies. 4. Clustering Genes over all Conditions only finds the strongest signals in the dataset as a whole. More ‘local’ signals within the data matrix may be missed. Inter-related(3) Z A B Y C X May represent more complex system such as: Local Signals(4)

• • How do we better model more complex systems? One technique that allows detection of all signals in the data is biclustering. Instead of clustering genes over all conditions biclustering clusters genes with respect to subsets of conditions. This enables better representation of: -interrelated clusters (genes may belong more than one bicluster). -local signals (genes correlated over only a few conditions). -noisy data (allows erratic genes to belong to no cluster).

Biclustering Conditions Gene 1 Gene 2 Gene 3 Gene 4 Gene 5 Gene 6 Gene 7 Gene 8 Gene 9 A B C D E FG H Clustering A B C D E G H Gene 1 Gene 4 Gene 9 Clustering misses local signal {(B, E, F), (1, 4, 6, 7, 9)} present over subset of conditions. Biclustering A B D B E F Gene 1 Gene 4 • Technique first described by J. A. Hartigan in 1972 and termed ‘Direct Clustering’. • First Introduced to Microarray expression data by Cheng and Church(2000) F Biclustering discovers local coherences over a subset of conditions Gene 9 Gene 1 Gene 4 Gene 6 Gene 7 Gene 9 E F G H

Approaches to Biclustering Microarray Gene Expression • First applied to Gene Expression Data by Cheng and Church(2000). – Used a sub-matrix scoring technique to locate biclusters. • Tanay et al. (2000) – Modelled the expression data on Bipartite graphs and used graph techniques to find ‘complete graphs’ or biclusters. • Lazzeroni and Owen – Used matrix reordering to represent different ‘layers’ of signals (biclusters) ‘Plaid Models’ to represent multiple signals within data. • Ben-Dor et al. (2002) – “Biclusters” depending on order relations (OPSM).

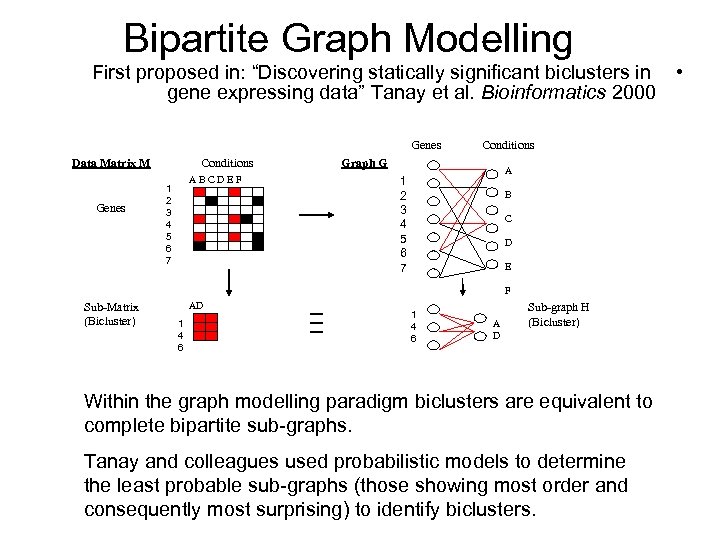Bipartite Graph Modelling First proposed in: “Discovering statically significant biclusters in • gene expressing data” Tanay et al. Bioinformatics 2000 Genes Data Matrix M Genes Conditions ABCDEF 1 2 3 4 5 6 7 Conditions Graph G A 1 2 3 4 5 6 7 B C D E F Sub-Matrix (Bicluster) AD 1 4 6 A D Sub-graph H (Bicluster) Within the graph modelling paradigm biclusters are equivalent to complete bipartite sub-graphs. Tanay and colleagues used probabilistic models to determine the least probable sub-graphs (those showing most order and consequently most surprising) to identify biclusters.

The Cheng and Church Approach The core element in this approach is the development of a scoring to prioritise sub-matrices. This scoring is based on the concept of the residue of an entry in a matrix. In the Matrix (I, J) the residue score of element In words, the residue of an entry is the value of the entry minus the row average, minus the column average, plus the average value in the matrix. This score gives an idea of how the value fits into the data in the surrounding matrix. J I i is given by: j a

The Cheng and Church Approach(2) The mean squared residue score (H) for a matrix (I, J) is then calculated : This Global H score gives an indication of how the data fits together within that matrix- whether it has some coherence or is random. A high H value signifies that the data is uncorrelated. - a matrix of equally spread random values over the range [a, b], has an expected H score of (b-a)/12. range = [0, 800] then H(I, J) = 53, 333 A low H score means that there is a correlation in the matrix - a score of H(I, J)= 0 would mean that the data in the matrix fluctuates in unison i. e. the sub-matrix is a bicluster

Worked example of H score: Matrix (M) Avg. = 6. 5 1 4 7 10 Col Avg. 2 5 8 11 3 6 9 12 Row Avg. 2 5 8 11 5. 4 6. 4 7. 4 R(1) = 1 - 2 - 5. 4 + 6. 5 = 0. 1 R(2) = 2 - 6. 4 + 6. 5 = 0. 1 : : R(12) = 12 - 11 -7. 4 + 6. 5 = 0. 1 H (M) = (0. 01 x 12)/12 = 0. 01 If 5 was replaced with 3 then the score would changed to: H(M 2) = 2. 06 If the matrix was reshuffled randomly the score would be around: H(M 3) = sqr(12 -1)/12 = 10. 08

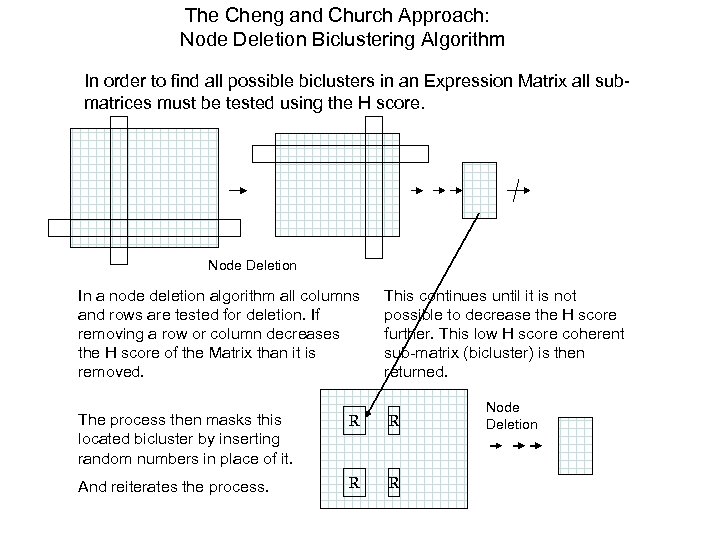The Cheng and Church Approach: Node Deletion Biclustering Algorithm In order to find all possible biclusters in an Expression Matrix all submatrices must be tested using the H score. Node Deletion In a node deletion algorithm all columns and rows are tested for deletion. If removing a row or column decreases the H score of the Matrix than it is removed. This continues until it is not possible to decrease the H score further. This low H score coherent sub-matrix (bicluster) is then returned. The process then masks this located bicluster by inserting random numbers in place of it. R R And reiterates the process. R R Node Deletion

The Cheng and Church Approach: Some results on lymphoma data (4026 96): No. of genes, no. of conditions 4, 96 10, 29 11, 25 103, 25 127, 13 13, 21 10, 57 2, 96 25, 12 9, 51 3, 96 2, 96

Conclusions: • High throughput Functional Genomics (Microarrays) requires Data Mining Applications. • Biclustering resolves Expression Data more effectively than single dimensional Cluster Analysis. • Cheng and Church Approach offers good base for future work. Future Research/Question’s: • Implement a simple H score program to facilitate study if H score concept. • Are there other alternative scorings which would better apply to gene expression data? • Have unbiclustered genes any significance? Horizontally transferred genes? • Implement full scale biclustering program and look at better adaptation to expression data sets and the biological context.

References • Basic microarray analysis: grouping and feature reduction by Soumya Raychaudhuri, Patrick D. Sutphin, Jeffery T. Chang and Russ B. Altman; Trends in Biotechnology Vol. 19 No. 5 May 2001 • Self Organizing Maps, Tom Germano, http: //davis. wpi. edu/~matt/courses/soms • “Data Analysis Tools for DNA Microarrays” by Sorin Draghici; Chapman & Hall/CRC 2003 • Self-Organizing-Feature-Maps versus Statistical Clustering Methods: A Benchmark by A. Ultsh, C. Vetter; FG Neuroinformatik & Kunstliche Intelligenz Research Report 0994

References • Interpreting patterns of gene expression with selforganizing maps: Methods and application to hematopoietic differentiation by Tamayo et al. • A Local Search Approximation Algorithm for k-Means Clustering by Kanungo et al. • K-means-type algorithms: A generalized convergence theorem and characterization of local optimality by Selim and Ismail