мат стат.pptx
- Количество слайдов: 7


Для того чтобы определиться с методами математико-статистической обработки данных нам нужно знать характер распределения. Параметры распределения – это его числовые характеристики, указывающие, где «в среднем» располагаются значения признака, насколько эти значения изменчивы и наблюдается ли преимущественное появление определенных значений признака. Помимо этого, по характеру распределения можно составить общее представление об общей характеристике выборки испытуемых по данному признаку и тому, насколько данная методика соответствует (т. е. «работает» , валидна) данной выборке.

Нормальное распределение характеризуется тем, что крайние значения признака в нем встречаются достаточно редко, а значения, близкие к средней величине достаточно часто. Нормальным такое распре деление называется потому, что оно очень часто встречалось в естест венно научных исследованиях и казалось "нормой" всякого массового случайного проявления признаков. Это распределение следует закону, открытому тремя учеными в разное время: Муавром в 1733 г. в Англии, Гауссом в 1809 г. в Германии и Лапласом в 1812 г. во Франции (Плохинский Н. А. , 1970, с. 17). График нормального распределения представляет собой привычную глазу психолога исследователя так на зываемую колообразную кривую. Параметры распределения это его числовые характеристики, указывающие, где "в среднем" располагаются значения признака, на сколько эти значения изменчивы и наблюдается ли преимущественное появление определенных значений признака. Наиболее практически важными параметрами являются математическое ожидание, дисперсия, показатели асимметрии и эксцесса. В реальных психологических исследованиях мы оперируем не па раметрами, а их приближенными значениями, так называемыми оценка ми параметров. Это объясняется ограниченностью обследованных выбо рок. Чем больше выборка, тем ближе может быть оценка параметра к его истинному значению. В дальнейшем, говоря о параметрах, мы будем иметь в виду юс оценки.
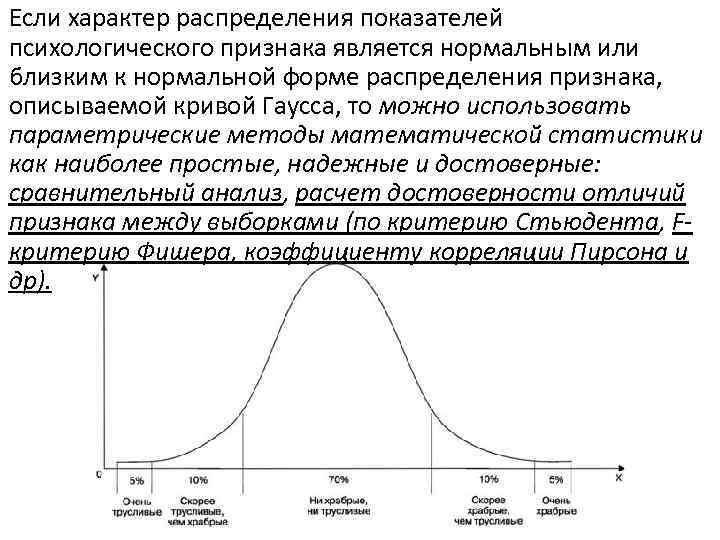
Если характер распределения показателей психологического признака является нормальным или близким к нормальной форме распределения признака, описываемой кривой Гаусса, то можно использовать параметрические методы математической статистики как наиболее простые, надежные и достоверные: сравнительный анализ, расчет достоверности отличий признака между выборками (по критерию Стьюдента, Fкритерию Фишера, коэффициенту корреляции Пирсона и др).
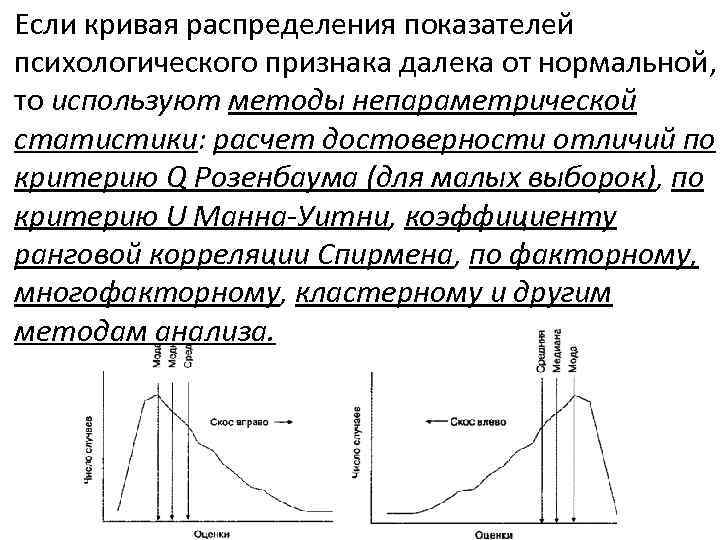
Если кривая распределения показателей психологического признака далека от нормальной, то используют методы непараметрической статистики: расчет достоверности отличий по критерию Q Розенбаума (для малых выборок), по критерию U Манна-Уитни, коэффициенту ранговой корреляции Спирмена, по факторному, многофакторному, кластерному и другим методам анализа.

- средняя арифметическая это величина, сумма отрицательных и положительных отклонений от которой равна нулю. В статистике ее обозначают буквой «М» или «X» . Чтобы ее подсчитать, надо суммировать все значения ряда и разделить сумму на количество суммированных значений; - среднее квадратичное отклонение (обозначаемое греческой буквой а (сигма) и называемое также основным, или стандартным отклонением) мера разнообразия входящих в группу объектов; она показывает, насколько в среднем отклоняется каждая варианта (конкретное значение оцениваемого параметра) от средней арифметической. Чем сильнее разбросаны варианты относительно средней, тем большим оказывается и среднее квадратичное отклонение. Разброс значений характеризует и размах, т. е. разность между наибольшим и наименьшим значением в ряду. Однако сигма полнее характеризует разброс значений относительно средней арифметической; - коэффициент вариации частное, полученное отделения сигмы на среднюю арифметическую, умноженное на 100% Коэффициент асимметрии показатель отклонения распределения в левую или правую сторону по оси абсцисс. Если правая ветвь кривой длиннее левой, говорят о правосторонней (положительной), если левая ветвь длиннее правой, говорят о левосторонней (отрицательной) асимметрии. -Эксцесс – мера остроты пика распределения случайной величины. Иной причиной больших показателей эксцесса и асимметрии может оказаться недостаточная надежность и валидность методик, используемых для данной популяции.

Спасибо за внимание!
мат стат.pptx