Diversification and the CAPM The relationship between risk

Introduction l Investors are concerned with – Risk – Returns l l What determines the required compensation for risk? It will depend on – The risks faced by investors – The tradeoff between risk and return they face © 1999 Thomas A. Rietz 2

Agenda l Concepts of risk for – A single stock – Portfolios of stocks l Risk for the diversified investor: Beta – Calculating Beta l The relationship between Beta and Return: The Capital Asset Pricing Model (CAPM) © 1999 Thomas A. Rietz 3

Overview l Investors demand compensation for risk – If investors hold “diversified” portfolios, risk can be defined through the interaction of a single investment with the rest of the portfolios through a concept called “beta” l The CAPM gives the required relationship between “beta” and the return demanded on the investment! © 1999 Thomas A. Rietz 4

Vocabulary l Expected return: l – What we expect to receive on average l Standard deviation of returns: – A measure of risk appropriate for diversified investors l Correlation – The tendency for two returns to fall above or below the expected return a the same or different times © 1999 Thomas A. Rietz Diversified investors – Investors who hold a portfolio of many investments – A measure of dispersion of actual returns l Beta l The Capital Asset Pricing Model (CAPM) – The relationship between risk and return for diversified investors 5

Measuring Expected Return l We describe what we expect to receive or the expected return: – Often estimated using historical averages (excel function: “average”).

Example: Die Throw l l Suppose you pay $300 to throw a fair die. You will be paid $100 x(The Number rolled) The probability of each outcome is 1/6. The returns are: – (100 -300)/300 = -66. 67% – (200 -300)/300 = -33. 33% …etc. l The expected return E(r) is: – 1/6 x(-66. 67%) + 1/6 x(-33. 33%) + 1/6 x 0% + 1/6 x 33. 33% + 1/6 x 66. 67% + 1/6 x 100% = 16. 67%!

Example: IEM l Suppose – You buy and AAPLi contract on the IEM for $0. 85 – You think the probability of a $1 payoff is 90% l The returns are: – (1 -0. 85)/0. 85 = 17. 65% – (0 -0. 85)/0. 85 = -100% l The expected return E(r) is: – 0. 9 x 17. 65% - 0. 1 x 100% = 5. 88%

Example: Market Returns l Recent data from the IEM shows the following average monthly returns from 5/95 to 10/99: – (http: //www. biz. uiowa. edu/iem/markets/compdata/compfund. html)

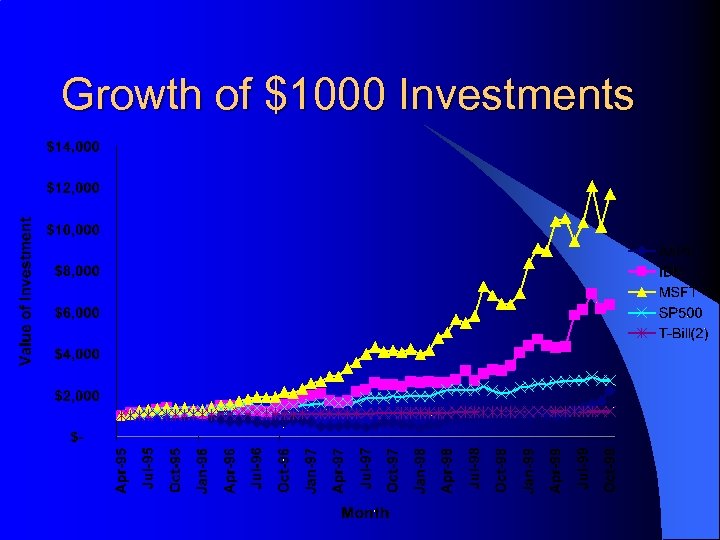
Growth of $1000 Investments

Measuring Risk: Standard Deviation and Variance l l Standard Deviation in Returns: Often estimated using historical averages (excel function: “stddev”)

Example: Die Throw l Recall the dice roll example: – – l You pay $300 to throw a fair die. You will be paid $100 x(The Number rolled) The probability of each outcome is 1/6. The expected return E(r) is 16. 67%. The standard deviation is:

Example: IEM l Suppose – You buy and AAPLi contract on the IEM for $0. 85 – You think the probability of a $1 payoff is 90% l The returns are: – (1 -0. 85)/0. 85 = 17. 65% – (0 -0. 85)/0. 85 = -100% l The expected return E(r) is: – 0. 9 x 17. 65% - 0. 1 x 100% = 5. 88% l The standard deviation is: – [0. 9 x(17. 65%)2 + 0. 1 x(-100%)2 - 5. 88%2]0. 5 = 35. 29%

Example: Market Returns l Recent data from the IEM shows the following average monthly returns & standard deviations from 5/95 to 10/99: – (http: //www. biz. uiowa. edu/iem/markets/compdata/compfund. html)

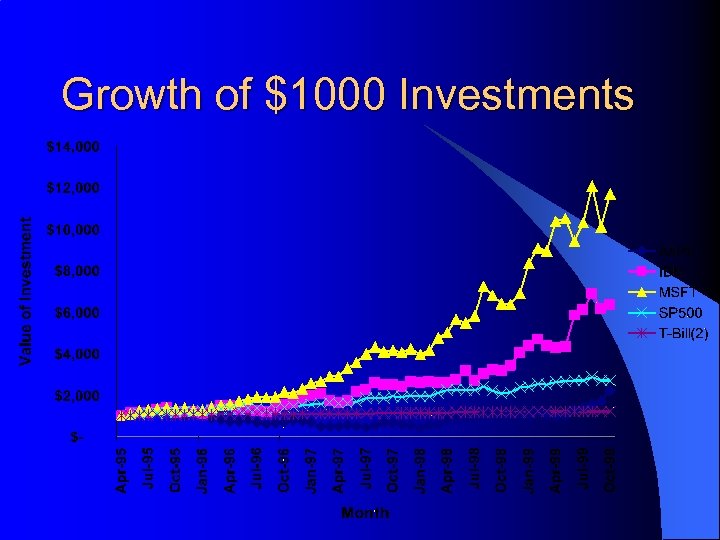
Growth of $1000 Investments

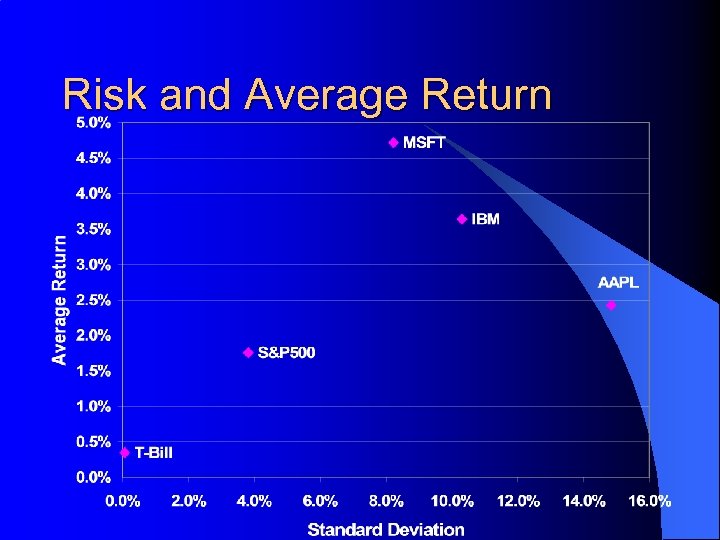
Risk and Average Return

Measures of Association l l Correlation shows the association across random variables Variables with – Positive correlation: tend to move in the same direction – Negative correlation: tend to move in opposite directions – Zero correlation: no particular tendencies to move in particular directions relative to each other

Covariance and Correlation l Covariance in returns, s. AB, is defined as: l The correlation, r. AB, is defined as: – r. AB is in the range [-1, 1] – Often estimated using historical averages (excel function: “correl”)

Notation for Two Asset and Portfolio Returns Item Actual Return Expected Return Variance Std. Dev. Asset A r. Ai E(r. A) s. A 2 s. A Correlation in Returns Covariance in Returns Asset B r. Bi E(r. B) s. B 2 s. B r. AB s. AB = s. As. Br. AB Portfolio r. Pi E(r. P) s. P 2 s. P

Example: IEM l Suppose – You buy an MSFT 090 i. H for $0. 85 and a MSFT 090 i. L contract for $0. 15. – You think the probability of $1 payoffs are 90% & 10% l The expected returns are: – 0. 9 x 17. 65% + 0. 1 x(-100%) = 5. 88% – 0. 1 x 566. 67% + 0. 9 x (-100%) = -33. 33% l The standard deviations are: – [0. 9 x(17. 65%)2 + 0. 1 x(-100%)2 - 5. 88%2]0. 5 = 35. 29% – [0. 1 x(566. 67%)2 + 0. 9 x(-100%)2 - (-33. 33%)2]0. 5 = 200% l The correlation is:

Example: Market Returns l Recent data from the IEM shows the following monthly return correlations from 5/95 to 10/99: – (http: //www. biz. uiowa. edu/iem/markets/compdata/compfund. html)

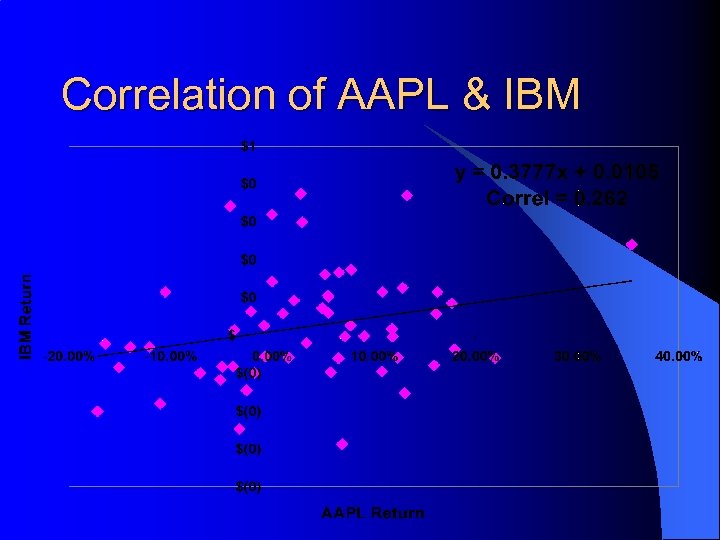
Correlation of AAPL & IBM

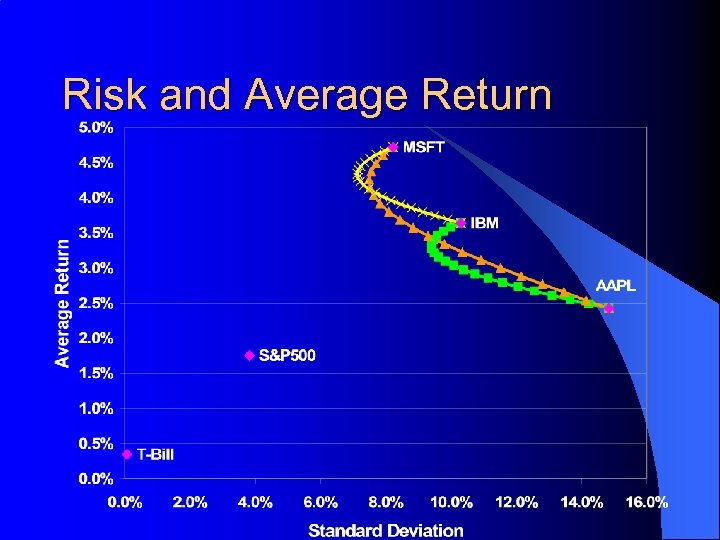
Risk and Average Return

Two Asset Portfolios: Risk l l The standard deviation is not a linear combination of the individual asset standard deviations Instead, it is given by: The standard deviation a the 50%/50%, AAPL & IBM portfolio is: The portfolio risk is lower than either individual asset’s because of diversification.

Correlations and Diversification l Suppose – E(r)A = 16% and s. A = 30% – E(r)B = 10% and s. B = 16% l Consider the E(r)P and s. P of securities A and B as w. A and r vary. . .

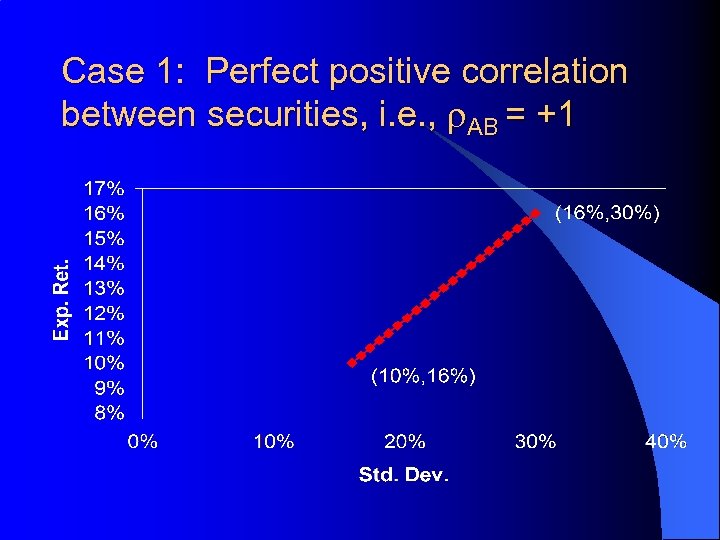
Case 1: Perfect positive correlation between securities, i. e. , r. AB = +1

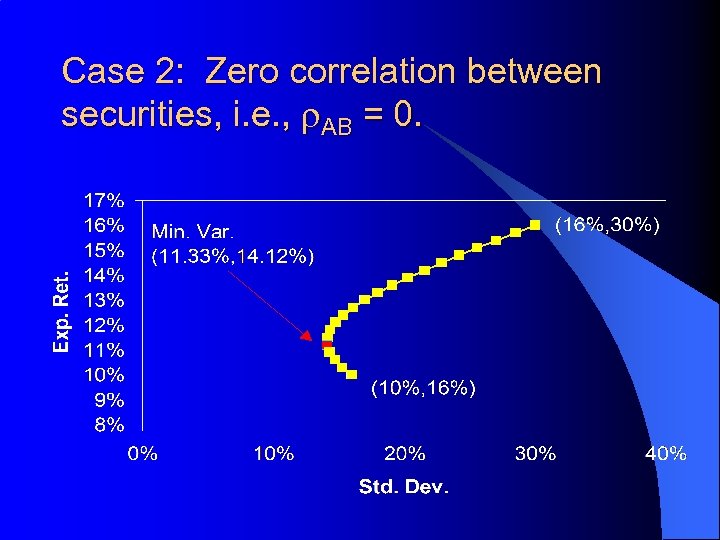
Case 2: Zero correlation between securities, i. e. , r. AB = 0.

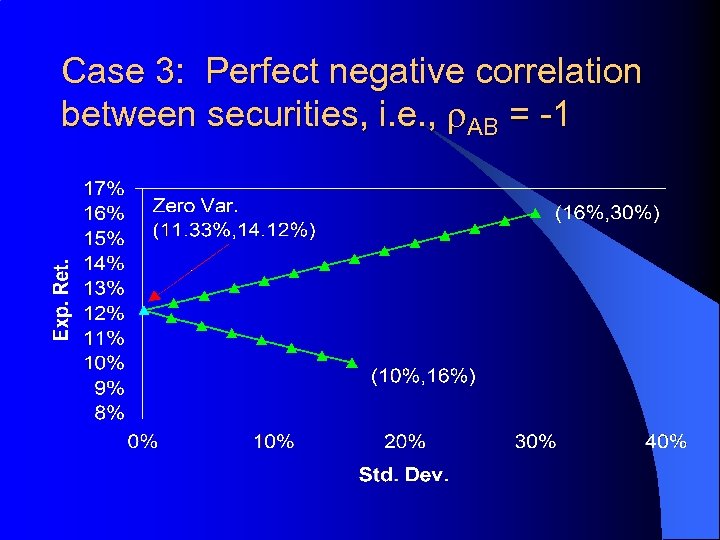
Case 3: Perfect negative correlation between securities, i. e. , r. AB = -1

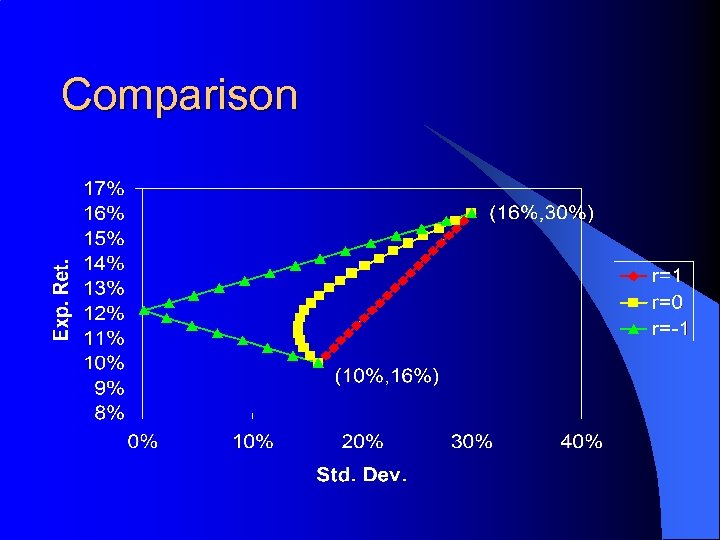
Comparison

$3 Asset Portfolios: Expected Returns and Standard Deviations l l Suppose the fractions of$

3 Asset Portfolios: Expected Returns and Standard Deviations l l Suppose the fractions of the portfolio are given by w. AAPL, w. IBM and w. MSFT. The expected return is: – E(r. P) = w. AAPLE(r. AAPL) + w. IBME(r. IBM) + w. MSFTE(r. MSFT) l The standard deviation is:

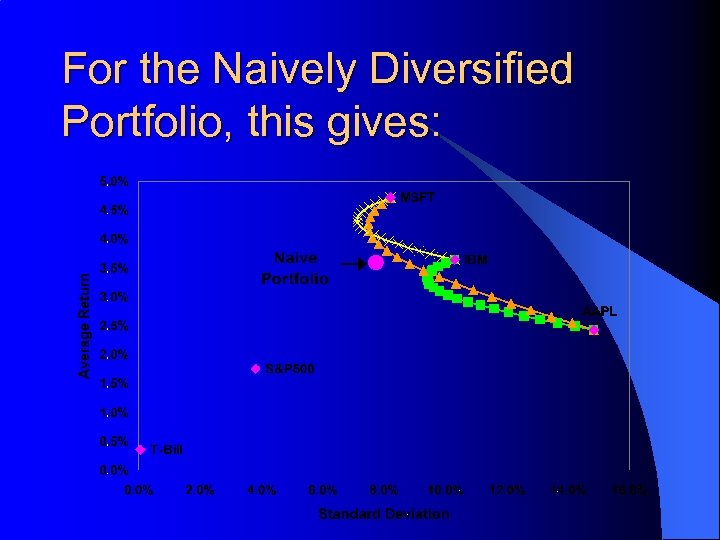
For the Naively Diversified Portfolio, this gives:

The Concept of Risk With N Risky Assets l As you increase the number of assets in a portfolio: – the variance rapidly approaches a limit, – the variance of the individual assets contributes less and less to the portfolio variance, and – the interaction terms contribute more and more. l l Eventually, an asset contributes to the risk of a portfolio not through its standard deviation but through its correlation with other assets in the portfolio. This will form the basis for CAPM.

Variance of a naively diversified portfolio of N assets l Portfolio variance consists of two parts: – 1. Non-systematic (or idiosyncratic) risk and – 2. Systematic (or covariance) risk l The market rewards only systematic risk because diversification can get rid of nonsystematic risk

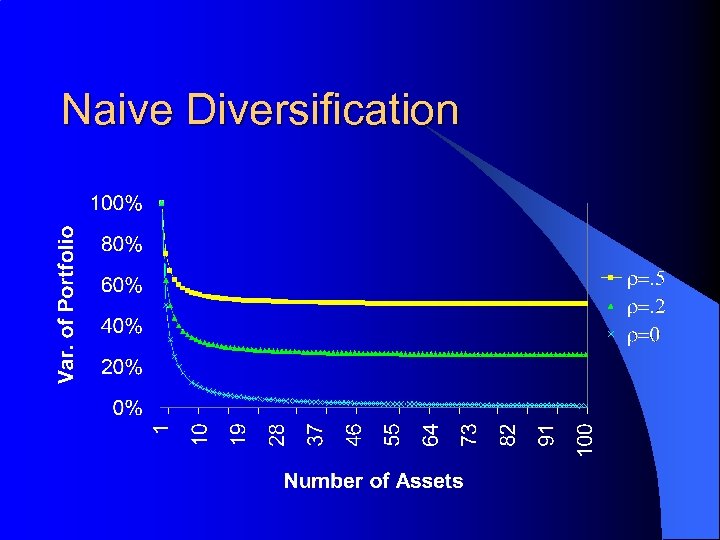
Naive Diversification

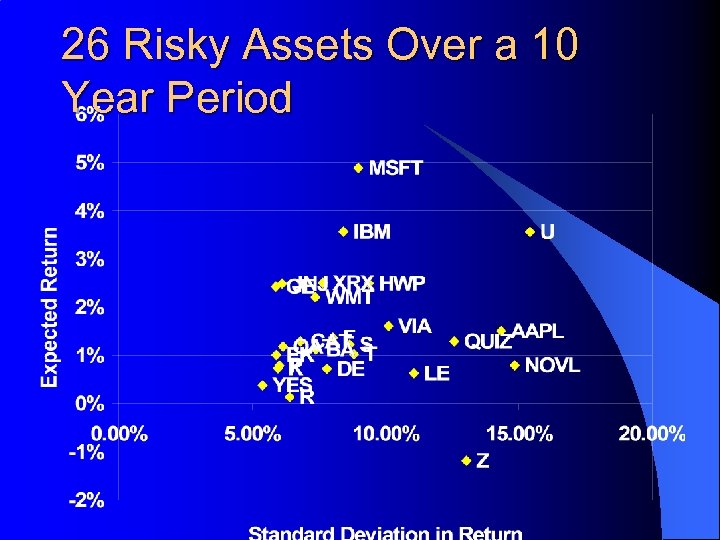
26 Risky Assets Over a 10 Year Period

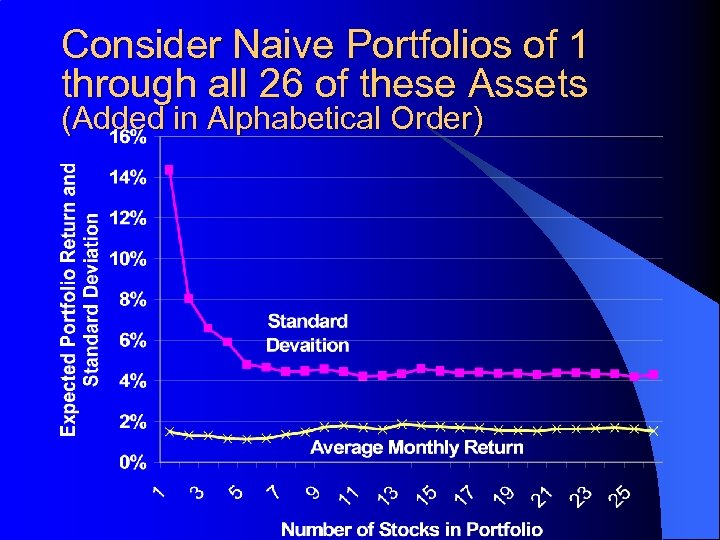
Consider Naive Portfolios of 1 through all 26 of these Assets (Added in Alphabetical Order)

The Capital Asset Pricing Model l CAPM Characteristics: – bi = sismrim/sm 2 l Asset Pricing Equation: – E(ri) = rf + bi[E(rm)-rf] l l CAPM is a model of what expected returns should be if everyone solves the same passive portfolio problem CAPM serves as a benchmark – Against which actual returns are compared – Against which other asset pricing models are compared

CAPM Assumptions l l No transactions costs No taxes Infinitely divisible assets Perfect competition – No individual can affect prices l Only expected returns and variances matter – Quadratic utility or – Normally distributed returns l l Unlimited short sales and borrowing and lending at the risk free rate of return Homogeneous expectations

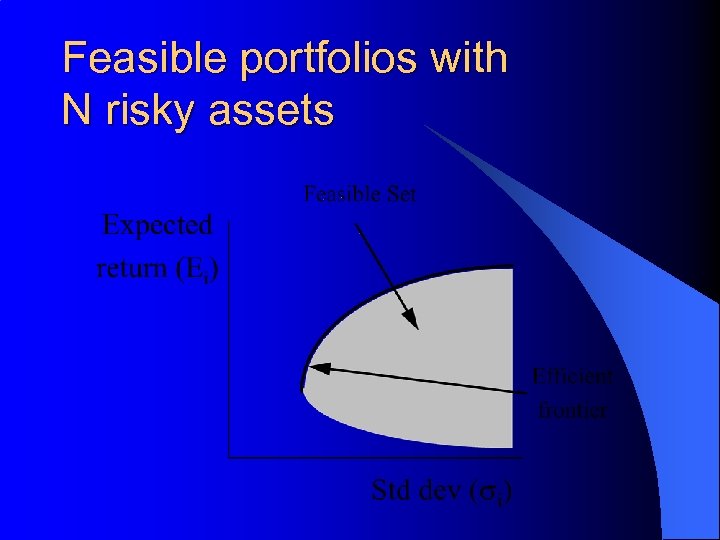
Feasible portfolios with N risky assets

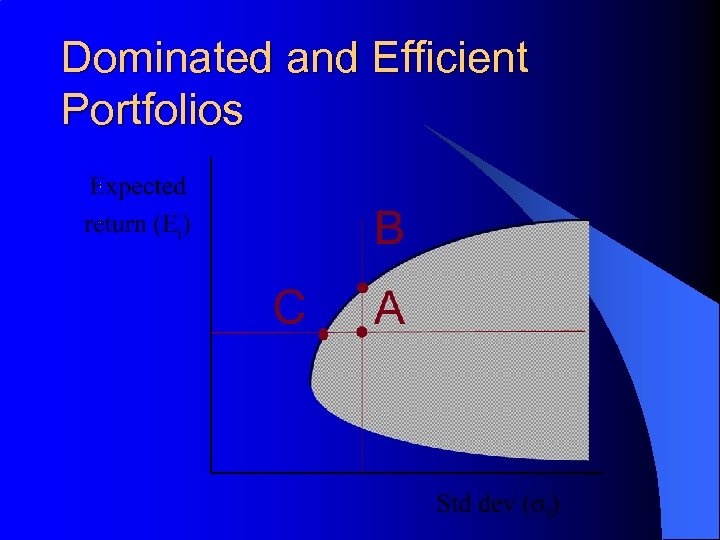
Dominated and Efficient Portfolios

How would you find the efficient frontier? 1. Find all asset expected returns and standard deviations. 2. Pick one expected return and minimize portfolio risk. 3. Pick another expected return and minimize portfolio risk. 4. Use these two portfolios to map out the efficient frontier.

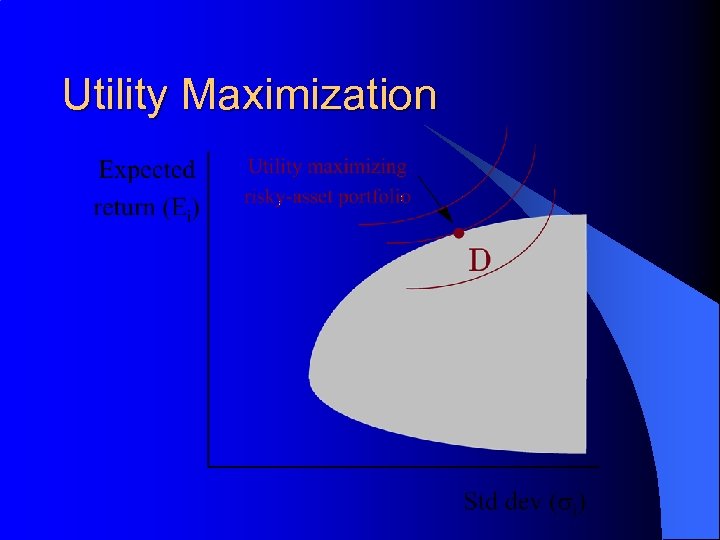
Utility Maximization

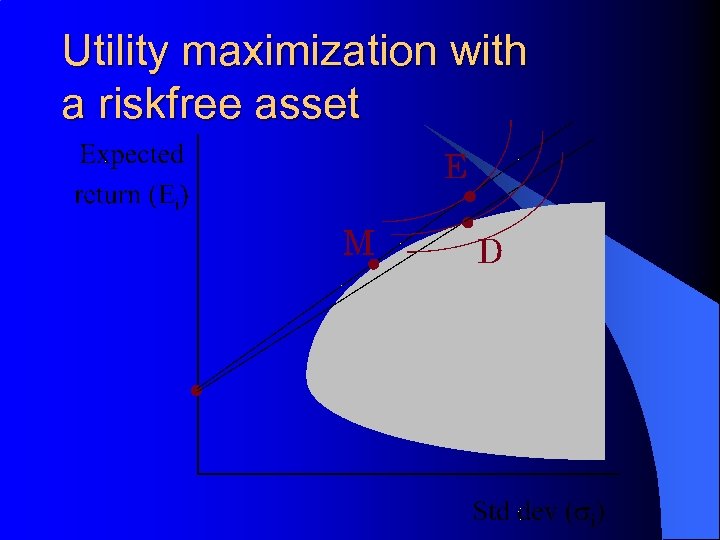
Utility maximization with a riskfree asset

Three Important Funds l l l The riskless asset has a standard deviation of zero The minimum variance portfolio lies on the boundary of the feasible set at a point where variance is minimum The market portfolio lies on the feasible set and on a tangent from the riskfree asset

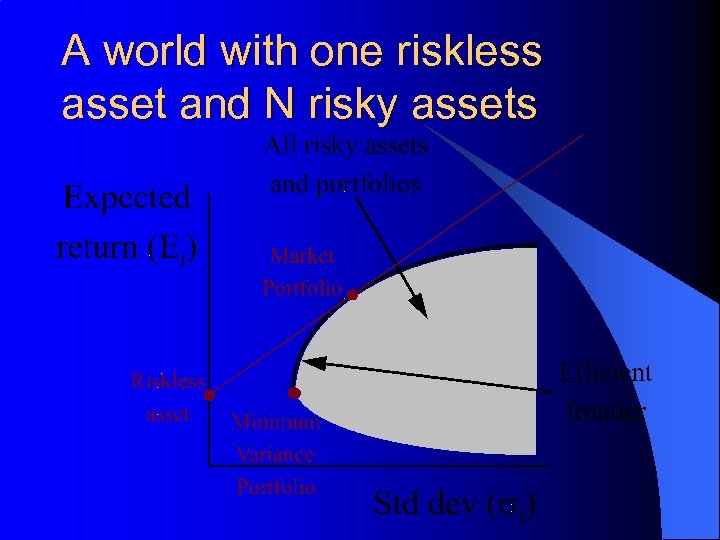
A world with one riskless asset and N risky assets

Tobin’s Two-Fund Separation l l l When the riskfree asset is introduced, All investors prefer a combination of 1) The riskfree asset and 2) The market portfolio Such combinations dominate all other assets and portfolios

The Capital Market Line l All investors face the same Capital Market Line (CML) given by:

Equilibrium Portfolio Returns l l The CML gives the expected return-risk combinations for efficient portfolios. What about inefficient portfolios? – Changing the expected return and/or risk of an individual security will effect the expected return and standard deviation of the market! l In equilibrium, what a security adds to the risk of a portfolio must be offset by what it adds in terms of expected return – Equivalent increases in risk must result in equivalent increases in returns.

How is Risk Priced? l l l Consider the variance of the market portfolio: It is the covariance with the market portfolio and not the variance of a security that matters Therefore, the CAPM prices the covariance with the market and not variance per se

The CAPM Pricing Equation! l l l The expected return on any asset can be written as: This is simply the no arbitrage condition! This is also known as the Security Market Line (SML).

Notes on Estimating b’s l l Let rit, rmt and rft denote historical returns for the time period t=1, 2, . . . , T. The are two standard ways to estimate historical b’s using regressions: – Use the Market Model: rit-rft = ai + bi(rmt-rft) + eit – Use the Characteristic Line: rit = ai + birmt + eit l l ai = ai + (1 -bi)rft and bi = bi Typical regression estimates: – Value Line (Market Model): l 5 Yrs, Weekly Data, VW NYSE as Market – Merrill Lynch (Characteristic Line): l 5 Yrs, Monthly Data, S&P 500 as Market

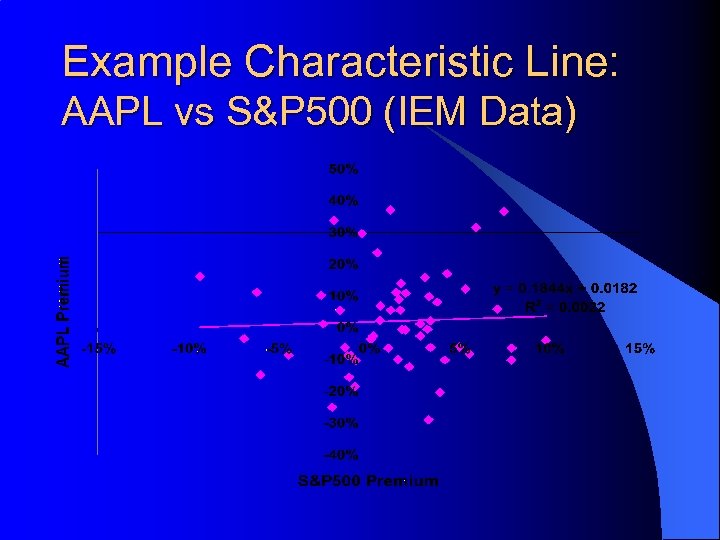
Example Characteristic Line: AAPL vs S&P 500 (IEM Data)

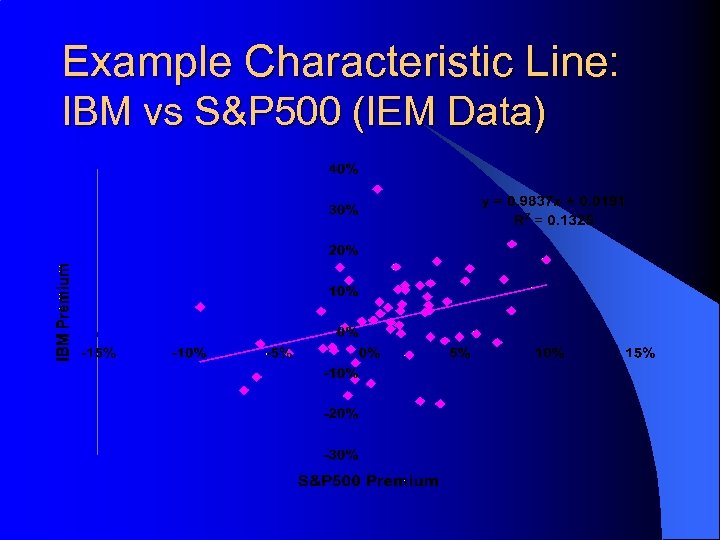
Example Characteristic Line: IBM vs S&P 500 (IEM Data)

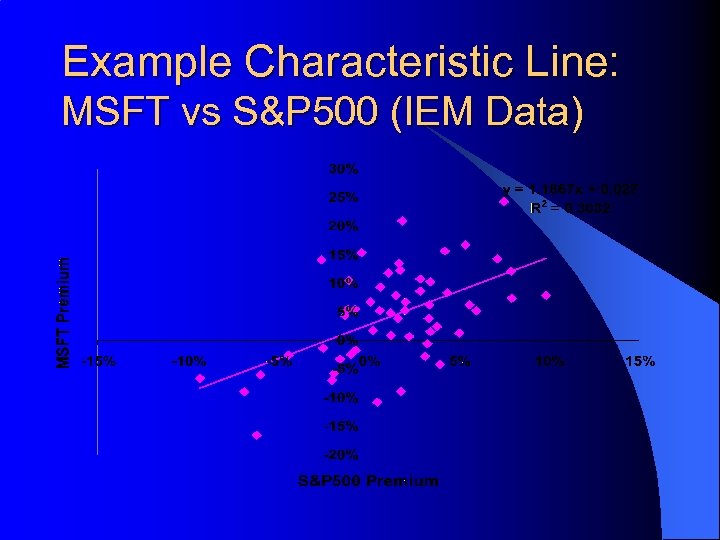
Example Characteristic Line: MSFT vs S&P 500 (IEM Data)

Notes on Estimating b’s l Betas for our companies AAPL 0. 1844 IBM MSFT SP 500 0. 9838 1. 1867 Raw: 1 Adjusted: 0. 4563 0. 9891 1. 1245 1 Avg. R: 2. 42% 3. 64% 4. 72% 1. 75%

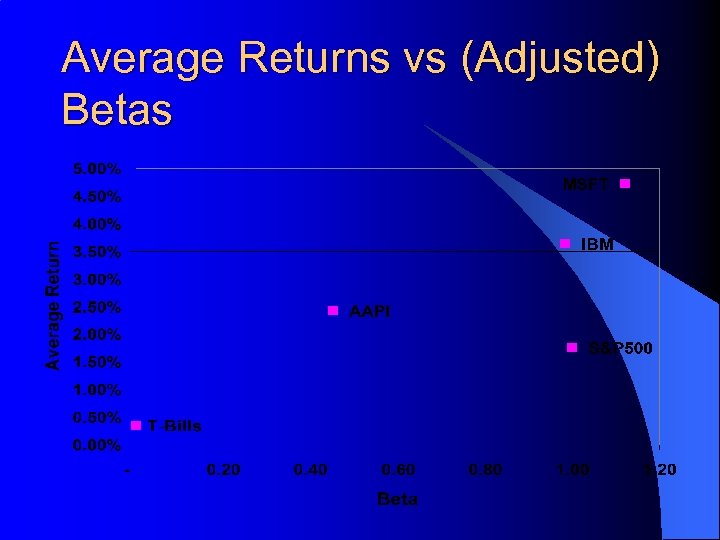
Average Returns vs (Adjusted) Betas