b97f80cd4be3143747f9464d0bbac189.ppt
- Количество слайдов: 25

Distributed Cooperative Control of Multiple Vehicle Formations Using Structural Potential Functions Reza Olfati-Saber Postdoctoral Scholar Control and Dynamical Systems California Institute of Technology Olfati@cds. caltech. edu UCLA, March 2 nd, 2002

Outline • • • Introduction Multi-vehicle Formations Past Research Coordinated Tasks – Stabilization/Tracking – Rejoin/Split/Reconfiguration Maneuvers Why Distributed Control? Formation Graphs – • • Rigidity/Foldability of Graphs Potential Functions Distributed Control Laws Simulation Results Conclusions

Introduction Definition: Multi-agent Systems are systems that consist of multiple agents or vehicles with several sensors/actuators and the capability to communicate with one another to perform coordinated tasks. Applications: – Automated highways – Air traffic control – Satellite formations – Search and rescue operations – Robots capable of playing games (e. g. soccer/capture the flag) – Formation flight of UAV’s (Unmanned Aerial Vehicles)
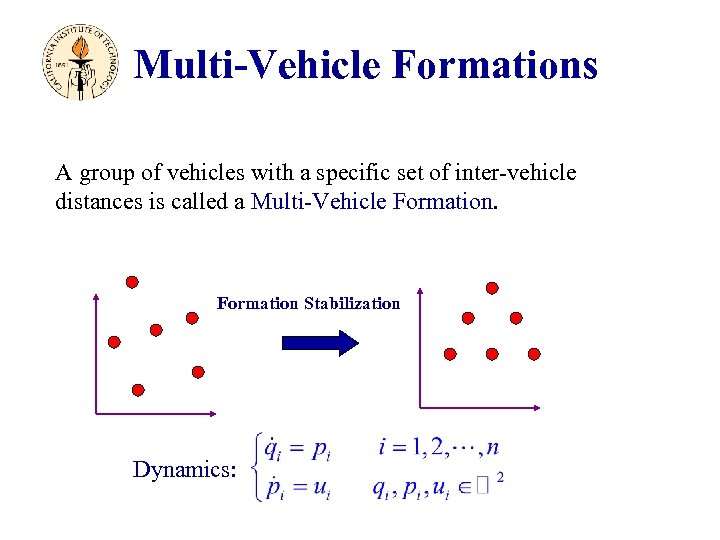
Multi-Vehicle Formations A group of vehicles with a specific set of inter-vehicle distances is called a Multi-Vehicle Formation Stabilization Dynamics:

Past Research • Robotics: navigation using artificial potential functions (Rimon and Koditschek, 1992) • Multi-vehicle Systems: – Coordinated control of groups using artificial potentials (Leonard and Fiorelli, 2001) – Information flow on graphs associated with multi-vehicle systems (Fax and Murray, 2001)

Why Distributed Control? • No vehicle knows the state/control of all other vehicles • No vehicle knows its relative configuration/velocity w. r. t. all other vehicles unless n = 2, 3 • The control law for each vehicle must be distributed so that the overall computational complexity of the problem is acceptable for large number of vehicles • A system controlled via a centeralized computer does not function if that computer breaks.
What is a Formation?

Formation Representation
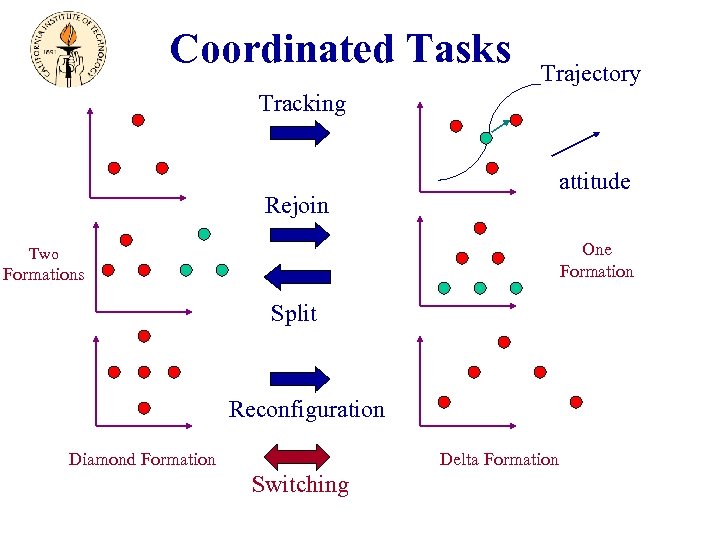
Coordinated Tasks Trajectory Tracking attitude Rejoin One Formation Two Formations Split Reconfiguration Delta Formation Diamond Formation Switching
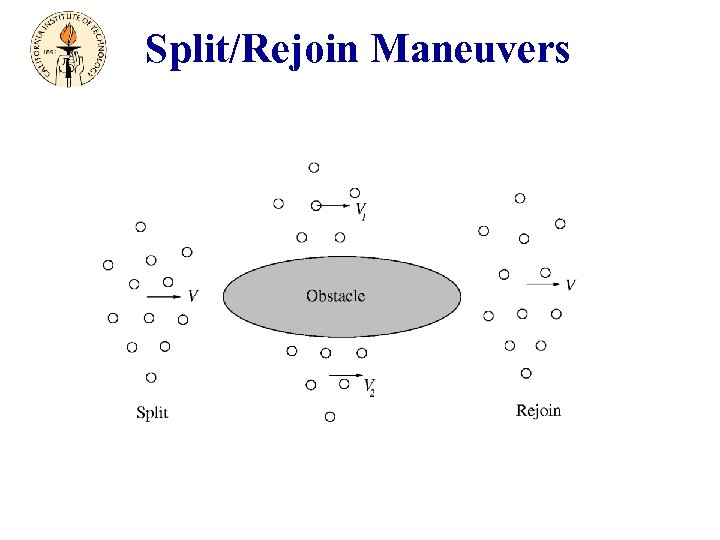
Split/Rejoin Maneuvers
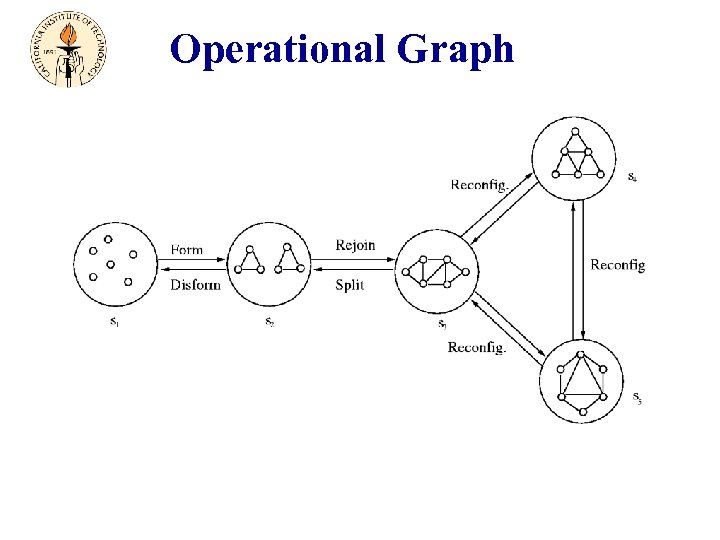
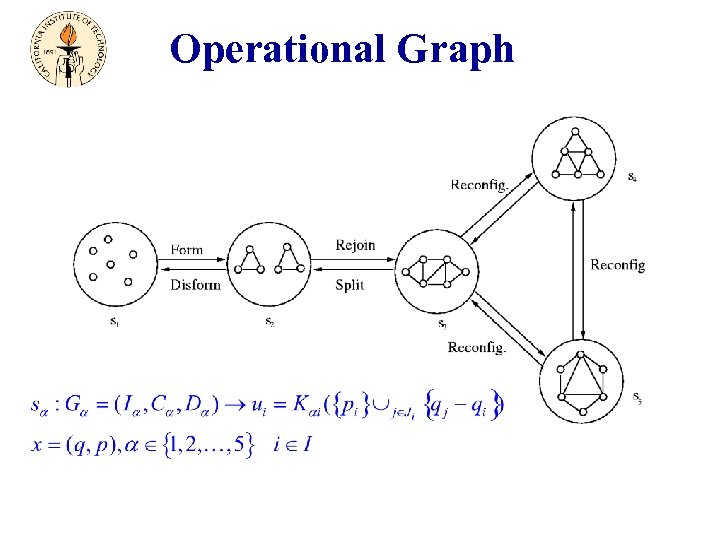
Operational Graph

Formation Graphs 1 an Edge means i) is a neighbor of ii) measures iii) knows its desired distance to 4 Formation Graph: Set of Vertices 3 2 Connectivity Matrix must be Distance Matrix

Rigidity Remark: c (or d) is called a single mobility degree of freedom of the formation graph. Definition: A planar formation graph with n nodes and 2 n-3 critical links is called a rigid formation graph. Definition: A critical link is a link that eliminates a mobility degree of freedom of a multi-body system. 1 a d 2 a 3 c b b 4

Foldability 1 Definition: The following non-redundant a a d set of equations are called structural constraints of a formation graph. 2 c b b Deviation Variable: 4 Definition: A rigid formation graph is foldable iff the set of structural constraints associated with the formation graph does not have a unique solution. 4 3
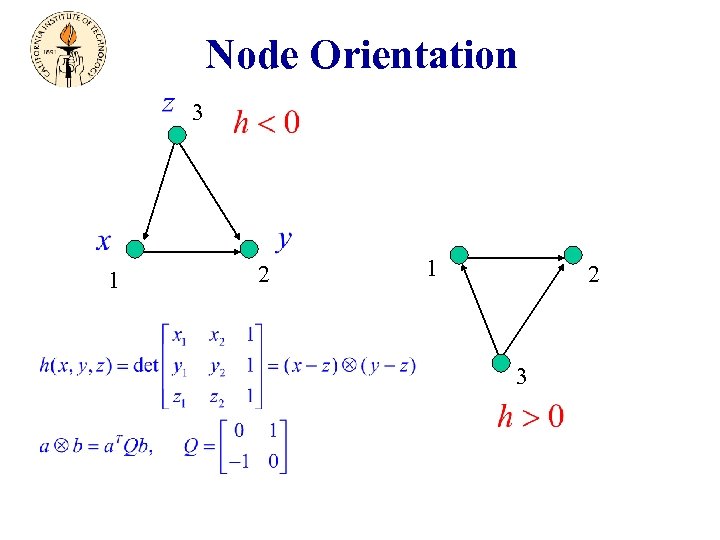
Node Orientation 3 1 2 3
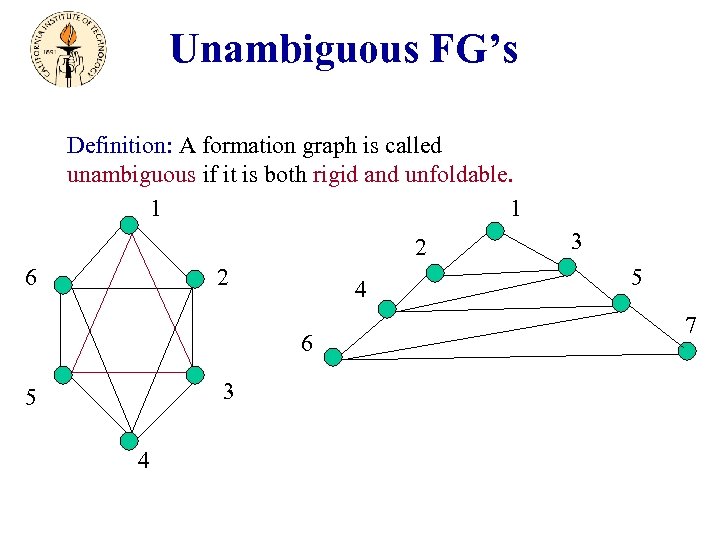
Unambiguous FG’s Definition: A formation graph is called unambiguous if it is both rigid and unfoldable. 1 1 2 6 2 4 6 3 5 4 3 5 7
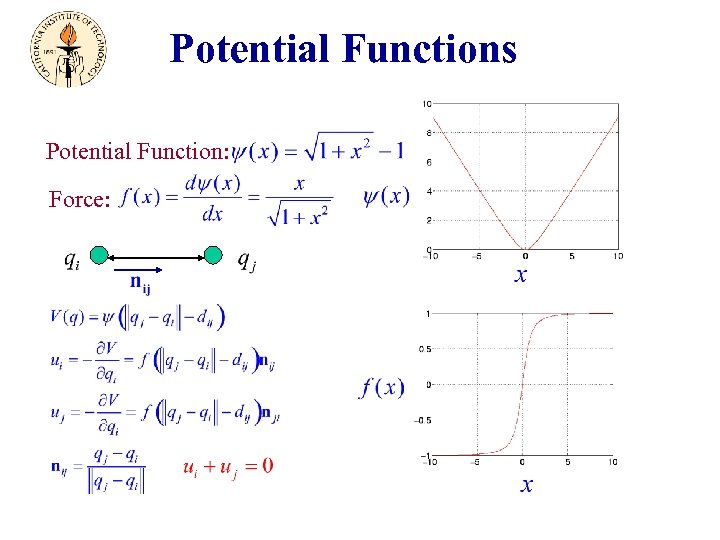
Potential Functions Potential Function: Force:

Distributed Control Laws Hamiltonian : Potential Function : indices of the neighbors of Theorem(ROS-RMM-IFAC’ 02): The following state feedback is a gradient-based bounded and distributed control law that achieves collision-free local asymptotic stabilization of any unambiguous desired formation graph.
Operational Graph
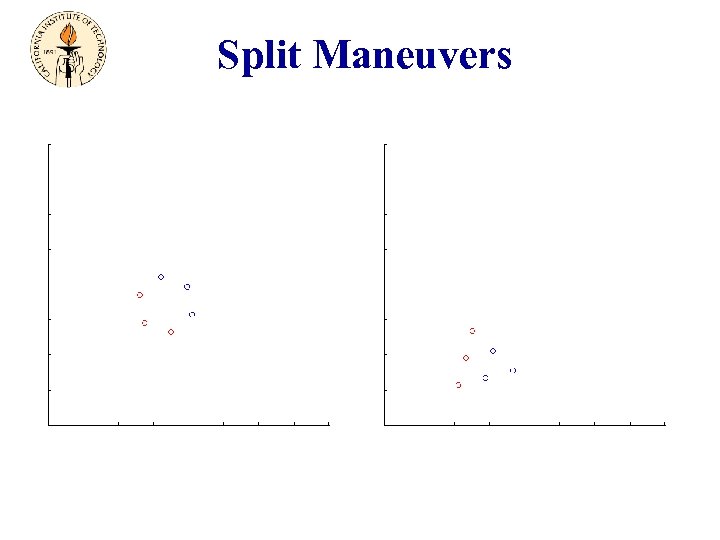
Split Maneuvers
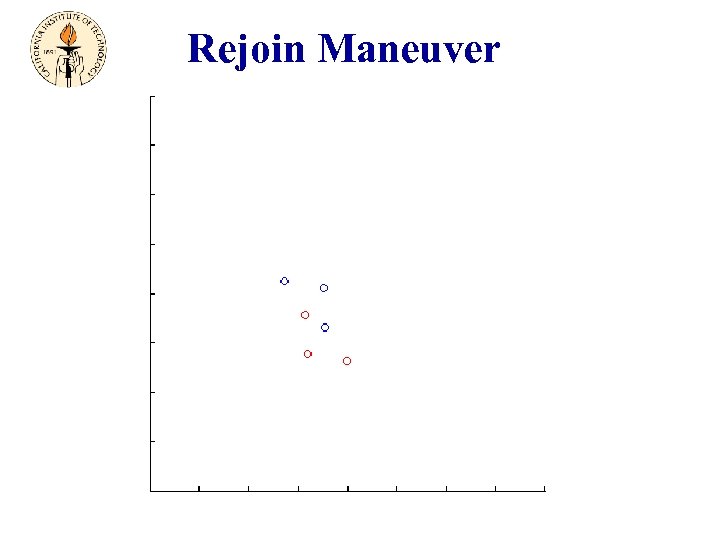
Rejoin Maneuver
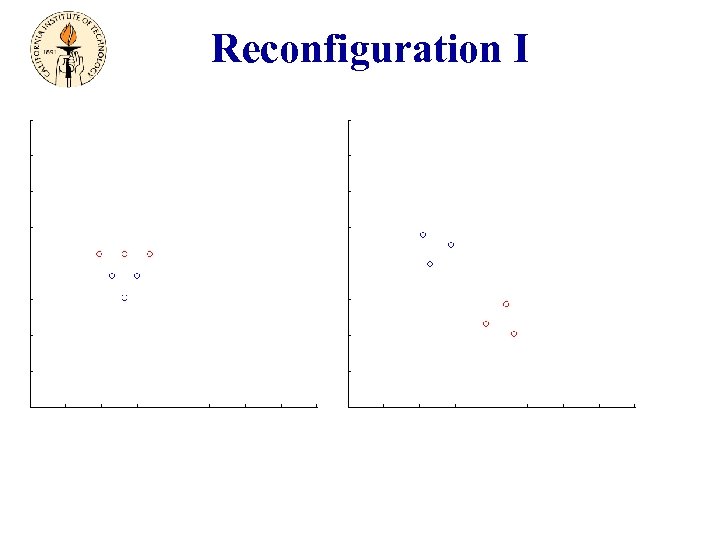
Reconfiguration I
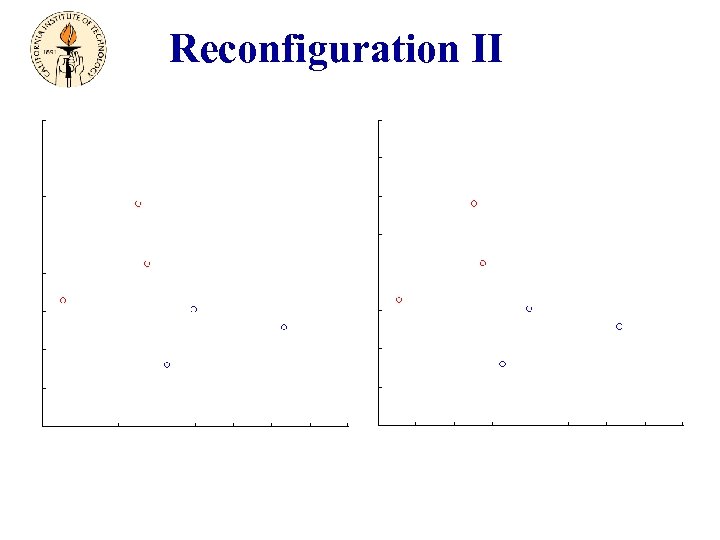
Reconfiguration II
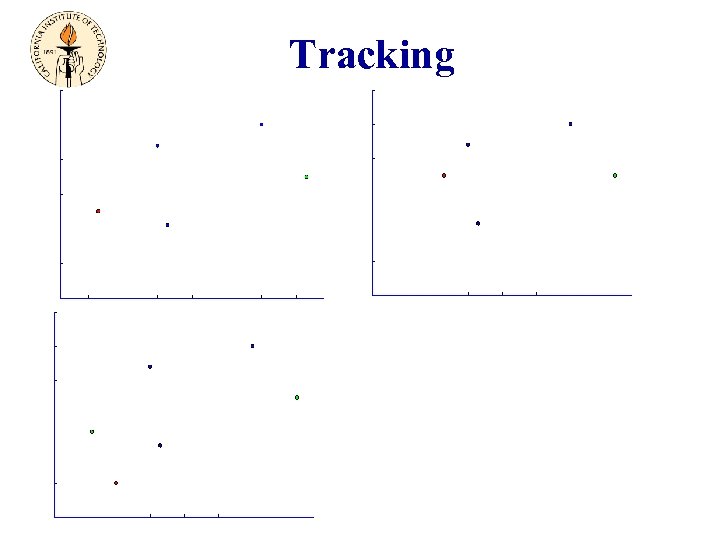
Tracking

Conclusions • Introducing a framework formal specification of unambiguous formation graphs of multi-vehicle systems that is compatible with formation control. • Providing a Lyapunov function and a bounded and distributed state feedback that performs coordinated tasks such as formation stabilization/tracking, split/rejoin, and reconfiguration maneuvers. • Introducing a Hybrid System that represents split, rejoin, and reconfiguration maneuvers in a unified framework as a discrete-state transition where each discrete-state is an unambiguous formation graph.
b97f80cd4be3143747f9464d0bbac189.ppt