4febf564367f1617a24748ce2a0304d9.ppt
- Количество слайдов: 32

Distributed Clustering for Robust Aggregation in Large Networks Ittay Eyal, Idit Keidar, Raphi Rom Technion, Israel
Aggregation in Sensor Networks – Applications Temperature sensors thrown in the woods Seismic sensors Grid computing load 2
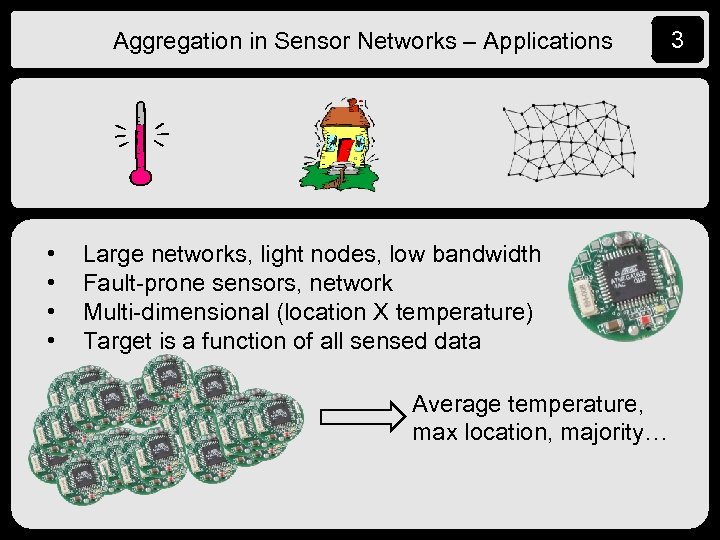
Aggregation in Sensor Networks – Applications • • Large networks, light nodes, low bandwidth Fault-prone sensors, network Multi-dimensional (location X temperature) Target is a function of all sensed data Average temperature, max location, majority… 3

What has been done?
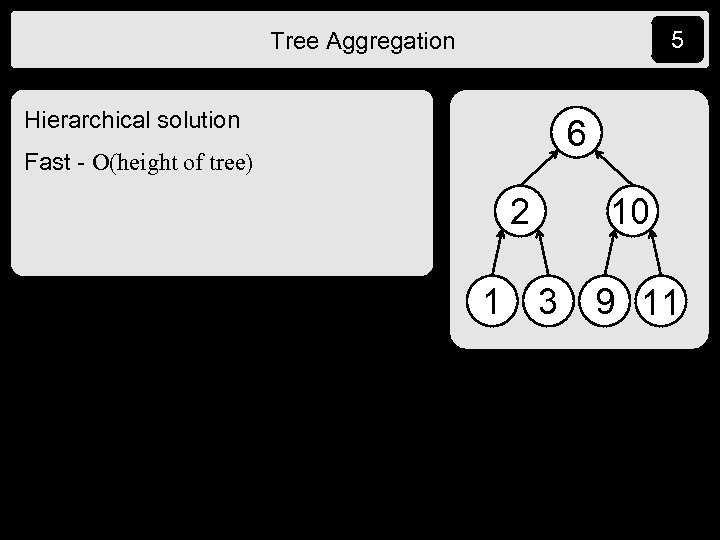
5 Tree Aggregation Hierarchical solution 6 Fast - O(height of tree) 2 1 10 3 9 11
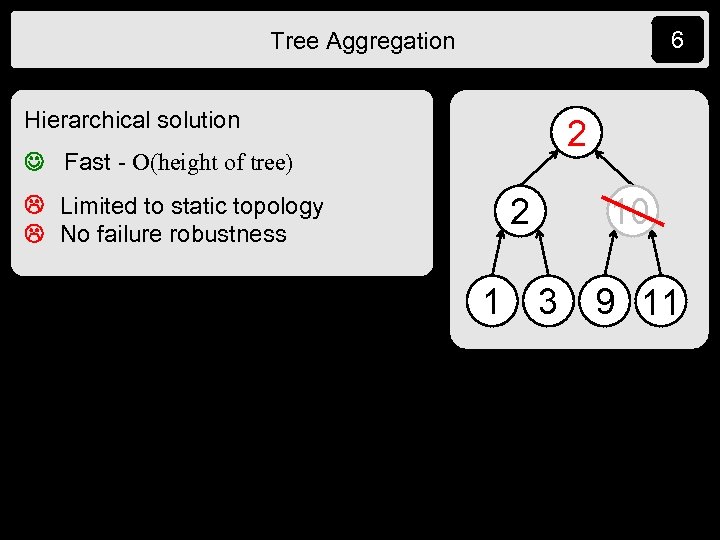
6 Tree Aggregation Hierarchical solution 2 6 Fast - O(height of tree) 2 Limited to static topology No failure robustness 1 10 3 9 11

7 Gossip: Each node maintains a synopsis 9 1 11 3 • • D. Kempe, A. Dobra, and J. Gehrke. Gossip-based computation of aggregate information. In FOCS, 2003. S. Nath, P. B. Gibbons, S. Seshan, and Z. R. Anderson. Synopsis diffusion for robust aggregation in sensor networks. In Sen. Sys, 2004.
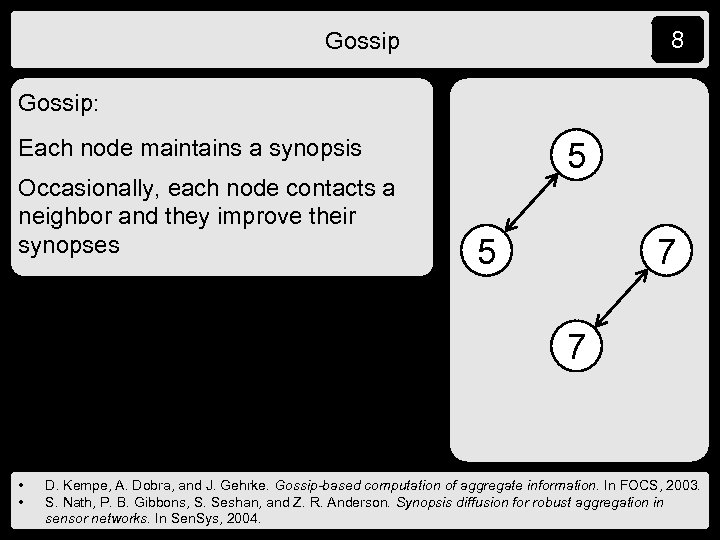
8 Gossip: Each node maintains a synopsis Occasionally, each node contacts a neighbor and they improve their synopses 5 9 5 1 11 7 7 3 • • D. Kempe, A. Dobra, and J. Gehrke. Gossip-based computation of aggregate information. In FOCS, 2003. S. Nath, P. B. Gibbons, S. Seshan, and Z. R. Anderson. Synopsis diffusion for robust aggregation in sensor networks. In Sen. Sys, 2004.
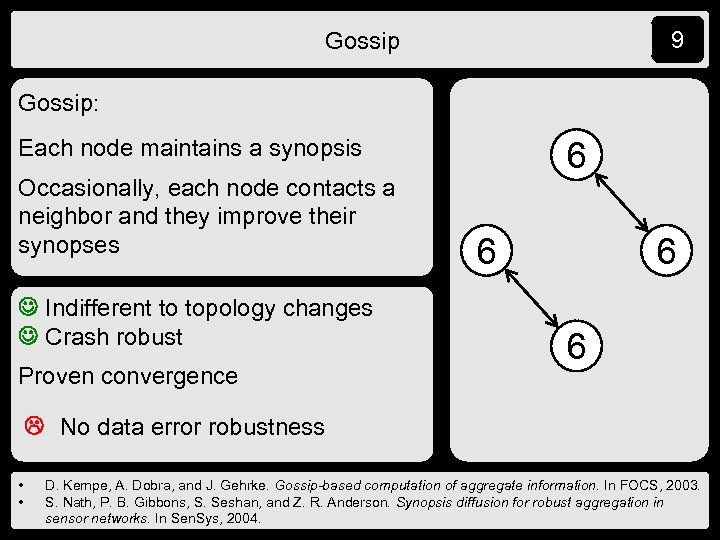
9 Gossip: Each node maintains a synopsis Occasionally, each node contacts a neighbor and they improve their synopses Indifferent to topology changes Crash robust Proven convergence 6 5 6 7 No data error robustness • • D. Kempe, A. Dobra, and J. Gehrke. Gossip-based computation of aggregate information. In FOCS, 2003. S. Nath, P. B. Gibbons, S. Seshan, and Z. R. Anderson. Synopsis diffusion for robust aggregation in sensor networks. In Sen. Sys, 2004.

A closer look at the problem

11 The Implications of Irregular Data A single erroneous sample can radically offset the data 1 4 106 3 The average (47 o) doesn’t tell the whole story 27 o 25 o 26 o 25 o 28 o 98 o 120 o 27 o
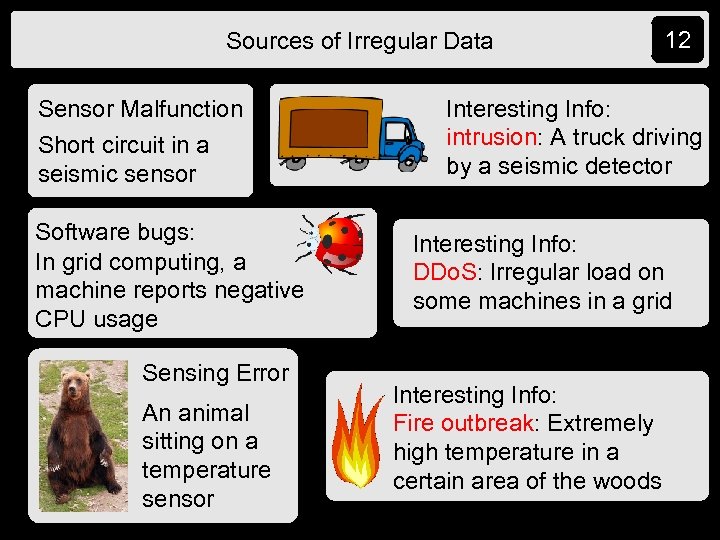
Sources of Irregular Data Sensor Malfunction Short circuit in a seismic sensor Software bugs: In grid computing, a machine reports negative CPU usage Sensing Error An animal sitting on a temperature sensor 12 Interesting Info: intrusion: A truck driving by a seismic detector Interesting Info: DDo. S: Irregular load on some machines in a grid Interesting Info: Fire outbreak: Extremely high temperature in a certain area of the woods
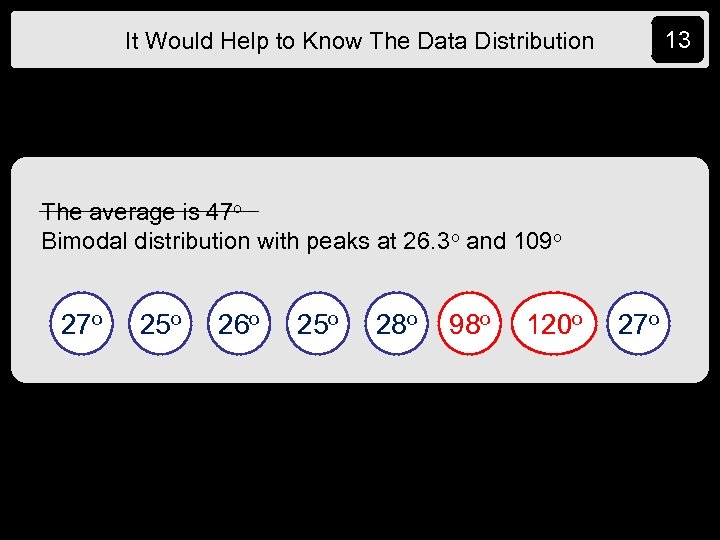
13 It Would Help to Know The Data Distribution The average is 47 o Bimodal distribution with peaks at 26. 3 o and 109 o 27 o 25 o 26 o 25 o 28 o 98 o 120 o 27 o
![Existing Distribution Estimation Solutions 14 Estimate a range of distributions [1, 2] or data Existing Distribution Estimation Solutions 14 Estimate a range of distributions [1, 2] or data](https://present5.com/presentation/4febf564367f1617a24748ce2a0304d9/image-14.jpg)
Existing Distribution Estimation Solutions 14 Estimate a range of distributions [1, 2] or data clustering according to values [3, 4] Fast aggregation [1, 2] Tolerate crash failures, dynamic networks [1, 2] High bandwidth [3, 4], multi-epoch [2, 3, 4] or One dimensional data only [1, 2] No data error robustness [1, 2] 1. 2. 3. 4. M. Haridasan and R. van Renesse. Gossip-based distribution estimation in peer-to-peer networks. In International. Workshop on Peer-to-Peer Systems (IPTPS 08), February 2008. J. Sacha, J. Napper, C. Stratan, and G. Pierre. Reliable distribution estimation in decentralised environments. Submitted for Publication, 2009. W. Kowalczyk and N. A. Vlassis. Newscast em. In Neural Information Processing Systems, 2004. N. A. Vlassis, Y. Sfakianakis, and W. Kowalczyk. Gossip-based greedy gaussian mixture learning. In Panhellenic Conference on Informatics, 2005.

Our Solution Estimate a range of distributions by data clustering according to values Fast aggregation Tolerate crash failures, dynamic networks Low bandwidth, single epoch Multi-dimensional data Data error robustness by outlier detection Outliers: Samples deviating from the distribution of the bulk of the data 15

16 Outlier Detection Challenge 27 o 25 o 26 o 25 o 28 o 98 o 120 o 27 o
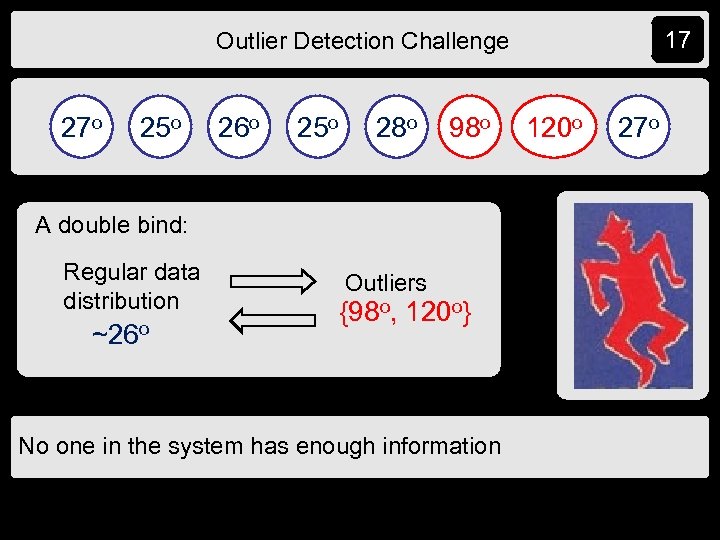
17 Outlier Detection Challenge 27 o 25 o 26 o 25 o 28 o 98 o A double bind: Regular data distribution ~26 o Outliers {98 o, 120 o} No one in the system has enough information 120 o 27 o
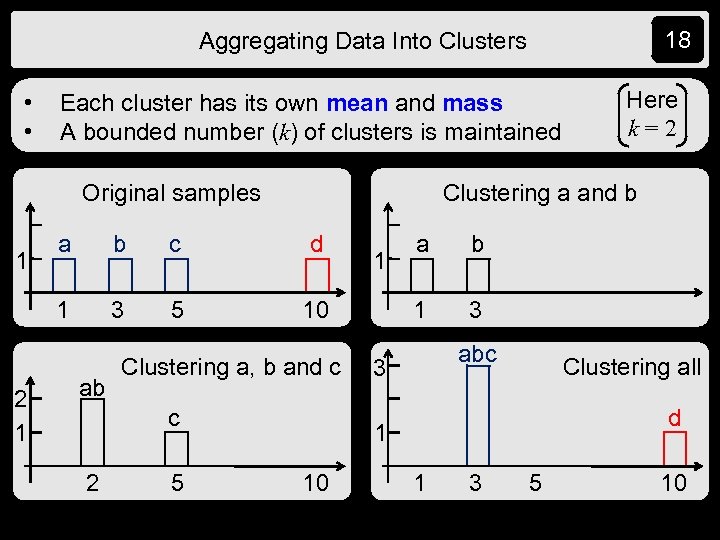
18 Aggregating Data Into Clusters • • Each cluster has its own mean and mass A bounded number (k) of clusters is maintained Clustering a and b Original samples 2 1 a b c d 1 1 3 5 10 ab Clustering a, b and c c 2 5 Here k=2 b 1 1 1 a 3 abc 3 Clustering all d 1 10 1 3 5 10
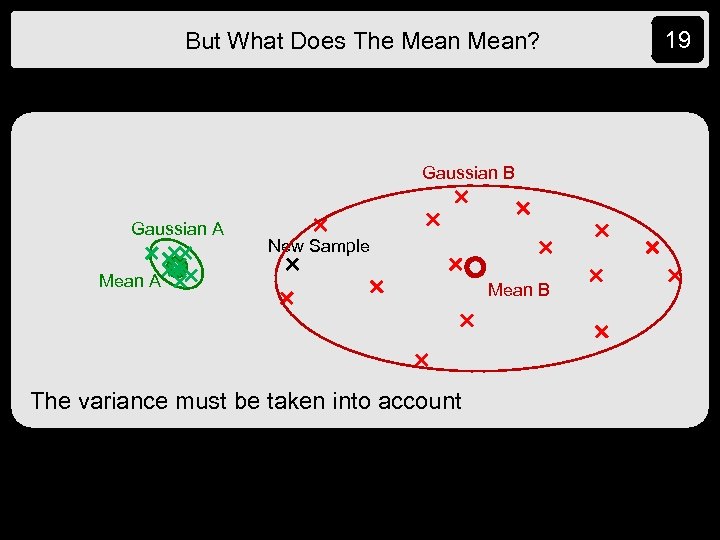
But What Does The Mean? Gaussian B Gaussian A New Sample Mean A The variance must be taken into account Mean B 19
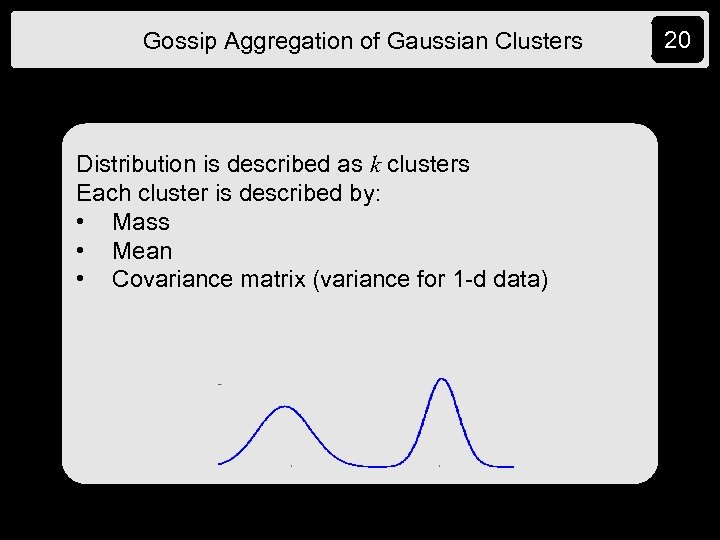
Gossip Aggregation of Gaussian Clusters Distribution is described as k clusters Each cluster is described by: • Mass • Mean • Covariance matrix (variance for 1 -d data) 20
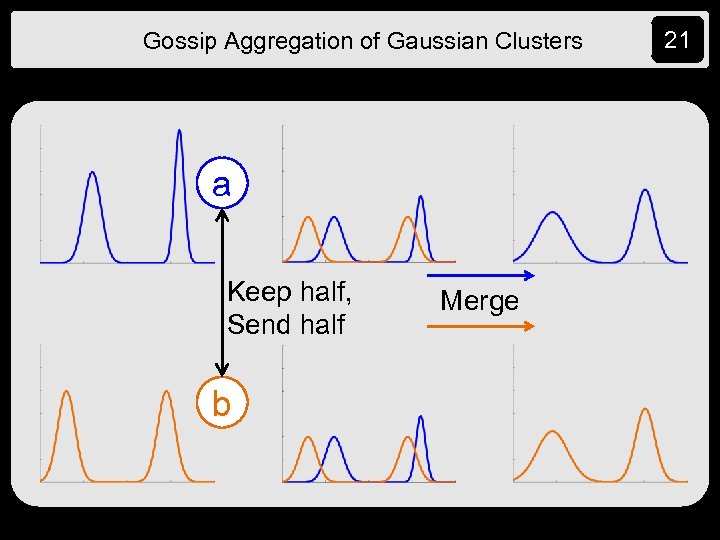
Gossip Aggregation of Gaussian Clusters a Keep half, Send half b Merge 21

Distributed Clustering for Robust Aggregation Our solution: • • Aggregate a mixture of Gaussian clusters Merge when necessary (exceeding k) By the time we need to merge, we can estimate the distribution Recognize outliers 22
Simulation Results: 1. Data error robustness 2. Crash robustness 3. Elaborate multidimensional data 23

It Works Where It Matters Not Interesting Easy 24
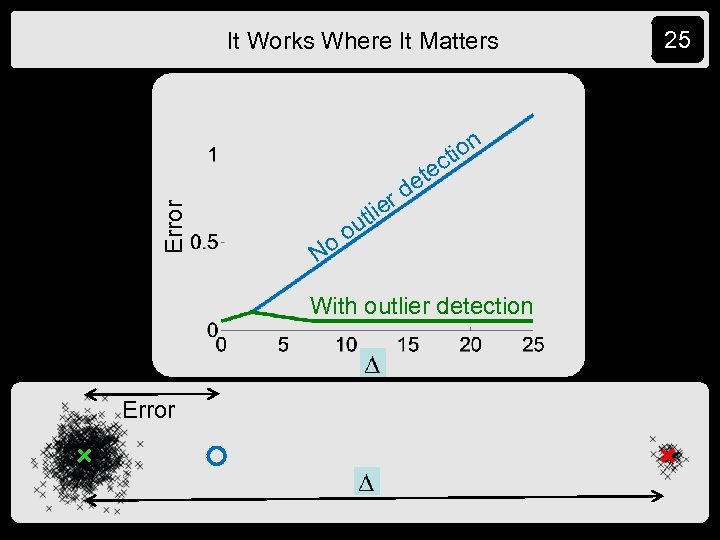
Error It Works Where It Matters ier utl ion t ec et d oo N With outlier detection Error 25

Simulation Results: 1. Data error robustness 2. Crash robustness 3. Elaborate multidimensional data 26
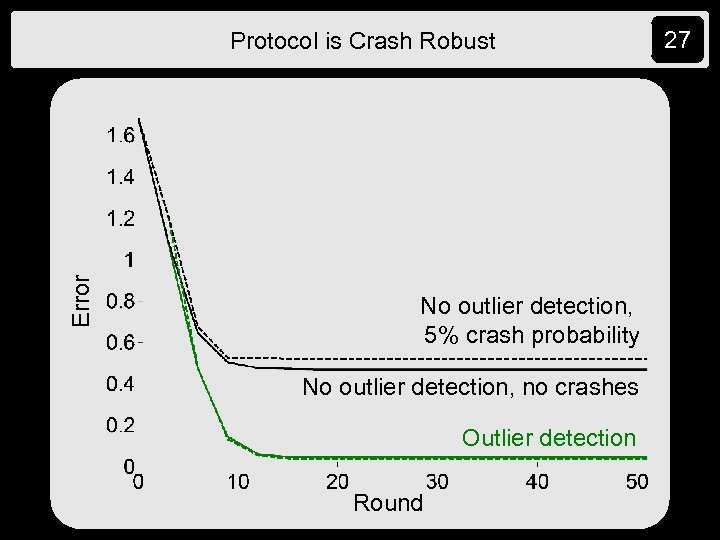
Error Protocol is Crash Robust No outlier detection, 5% crash probability No outlier detection, no crashes Outlier detection Round 27

Simulation Results: 1. Data error robustness 2. Crash robustness 3. Elaborate multidimensional data 28
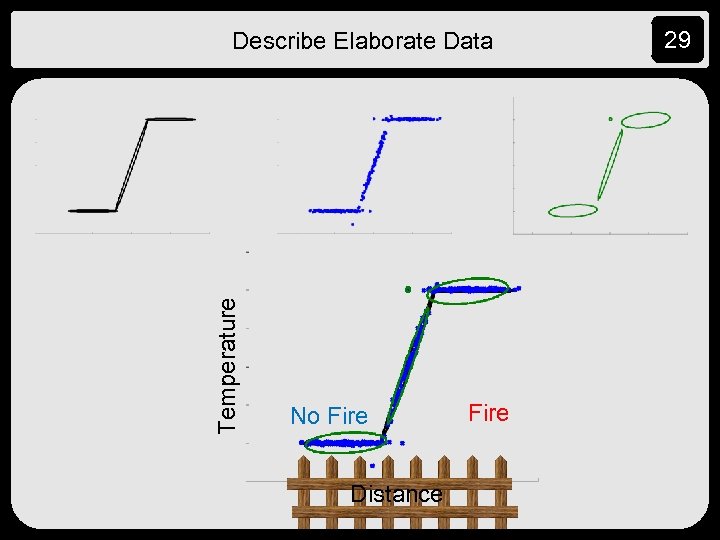
Temperature Describe Elaborate Data No Fire Distance Fire 29

Theoretical Results (In Progress) 30 The algorithm converges • Eventually all nodes have the same clusters forever • Note: this holds even without atomic actions • The invariant is preserved by both send and receive … to the “right” output (where it matters) • If outliers are “far enough” from other samples, then they are never mixed into non-outlier clusters • They are discovered • They do not bias the good samples’ aggregate
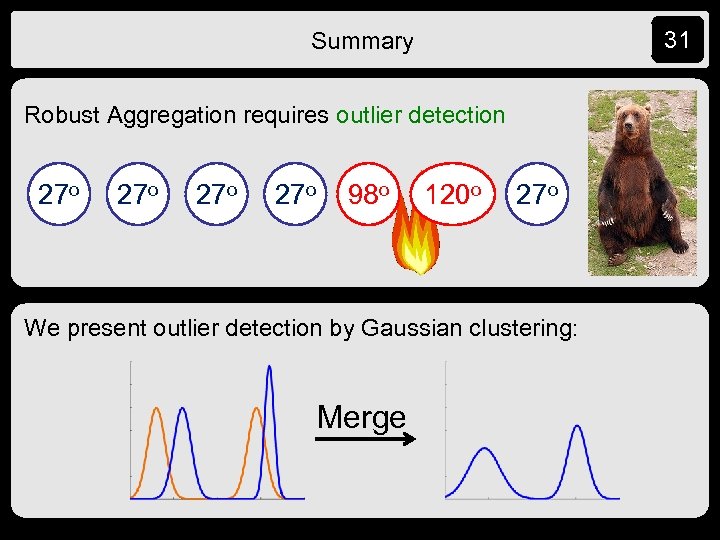
31 Summary Robust Aggregation requires outlier detection 27 o 27 o 98 o 120 o 27 o We present outlier detection by Gaussian clustering: Merge
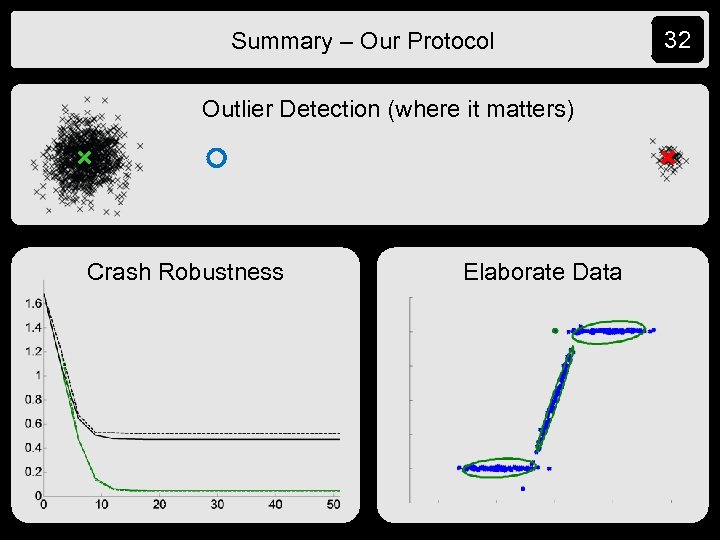
Summary – Our Protocol Outlier Detection (where it matters) Crash Robustness Elaborate Data 32
4febf564367f1617a24748ce2a0304d9.ppt