09c88f1547ffdaaea1fe5e33f0e350ea.ppt
- Количество слайдов: 21

Distributed Asymmetric Verification in Computational Grids Michael Kuhn Stefan Schmid Roger Wattenhofer Distributed Computing Group IPDPS 2008 Miami, Florida, USA 1

Grid Computing • Goal: Use idle computing resources worldwide – Examples: seti@home, folding@home, . . . Michael Kuhn, ETH Zurich @ IPDPS 2008 2 2
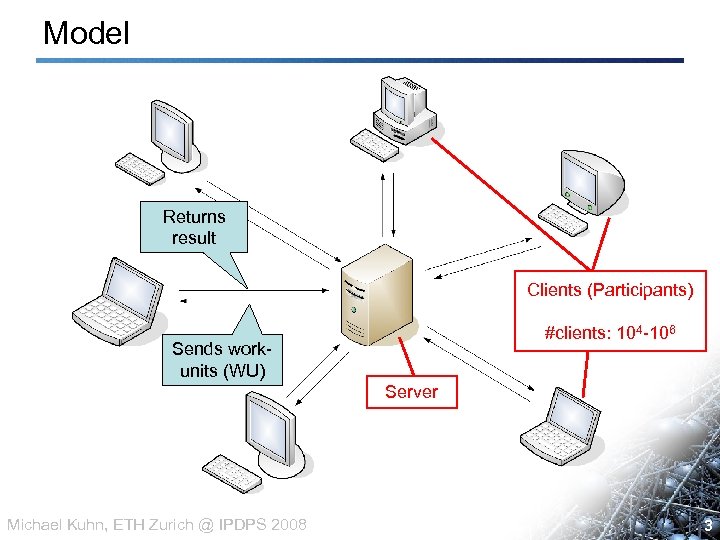
Model Returns result Clients (Participants) #clients: 104 -106 Sends workunits (WU) Server Michael Kuhn, ETH Zurich @ IPDPS 2008 3 3

The Problem of Cheaters • Why should people participate? – Incentives: honour („user of the day“), money, . . . • But: Incentives attract cheaters! Michael Kuhn, ETH Zurich @ IPDPS 2008 4 4
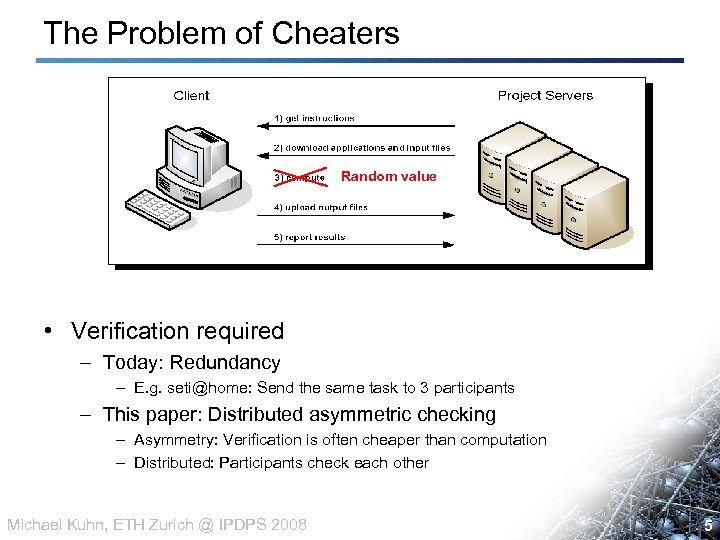
The Problem of Cheaters Random value • Verification required – Today: Redundancy – E. g. seti@home: Send the same task to 3 participants – This paper: Distributed asymmetric checking – Asymmetry: Verification is often cheaper than computation – Distributed: Participants check each other Michael Kuhn, ETH Zurich @ IPDPS 2008 5 5

Contributions • Distributed checking algorithm integrated in BOINC – Faster than redundancy if asymmetric checking function exists – Better guarantees than typically used redundancy schemes • Resistant against – Dominance of seemingly fast clients – Lazy checking – Sybil attacks • Proof-of-concept implementation for discrete logarithm problem – Asymmetric checking function for Pollard-rho algorithm Michael Kuhn, ETH Zurich @ IPDPS 2008 6 6
![Related Work • Cheating is a problem [Kahney, Wired Magazine, Feb. 2001] – Seti@home: Related Work • Cheating is a problem [Kahney, Wired Magazine, Feb. 2001] – Seti@home:](https://present5.com/presentation/09c88f1547ffdaaea1fe5e33f0e350ea/image-7.jpg)
Related Work • Cheating is a problem [Kahney, Wired Magazine, Feb. 2001] – Seti@home: more than 50% of resources spent on cheating! • Ringer scheme (precompute selected results) [Golle and Mironov, CT-RSA‘ 01], [Szaja et al. , SP‘ 03] – Additional work on the server (precomputing ringers) • Commitment scheme with Merkle-tree [Du et al. , ICDCS‘ 04] – Additional work on the server (recompute some work-units) • Cryptographic protocols e. g. [Aiello et al, ICALP‘ 00], [Cachin et al. , EUROCRYPT‘ 99] – Often computationally too expensive in practice Michael Kuhn, ETH Zurich @ IPDPS 2008 7 7

Challenges • Cheaters seem to be much faster than ordinary participants – 1% cheaters can submit >99% of the results • Cheaters stay honest for a long time, and only then start to cheat – Opens many possibilities for cheaters – Never trust a participant • Lazy checking – Cheaters can calculate everything correctly but cheat during verification (i. e. simply say the result was correct) Michael Kuhn, ETH Zurich @ IPDPS 2008 8 8
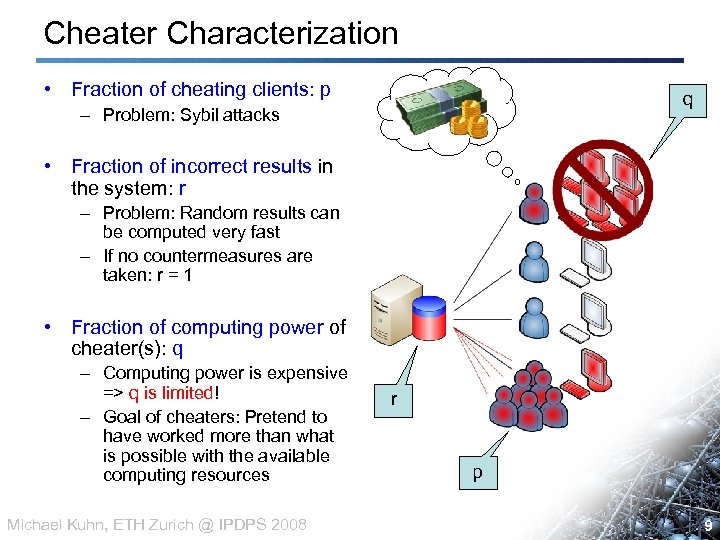
Cheater Characterization • Fraction of cheating clients: p q – Problem: Sybil attacks • Fraction of incorrect results in the system: r – Problem: Random results can be computed very fast – If no countermeasures are taken: r = 1 • Fraction of computing power of cheater(s): q – Computing power is expensive => q is limited! – Goal of cheaters: Pretend to have worked more than what is possible with the available computing resources Michael Kuhn, ETH Zurich @ IPDPS 2008 r p 9 9

Asymmetric Verification • Performance property: It is much cheaper to verify the correctness of a result than to calculate the result – Asymmetric • Fingerprint property: A verifier calculates a fingerprint rather than a boolean result – Server compares fingerprints Example: – Only honestly computed checks can {7, 7, 13, positive result Task: Find prime factors of x = 10829; Solution: lead to a 17} – Observe: Collusions Fingerprint: 7 Checking input: {7, 7, 13, 17}; still possible * 7 * 13 * 17 = 10829 • Uniqueness property: Results are either inherently unique, or the dependence from the input values can be verified – Prevents replay attacks Michael Kuhn, ETH Zurich @ IPDPS 2008 10 10

Distributed Verification: Algorithm • Prerequisites – Fraction of cheaters is limited and considerably smaller than 50% (e. g. p ≤ 10%) => details later – Punishment is possible • Check each result, until a clear decision is possible – Result good if „considerably more“ positive than negative checks (and vice versa) – As p is limited, high probability of correct decision (see paper for details) – Punish cheaters (including colluders) and remove all their pending results • Assign checks uniformly at random among active clients – Fast clients (often cheaters) cannot dominate checking Michael Kuhn, ETH Zurich @ IPDPS 2008 11 11
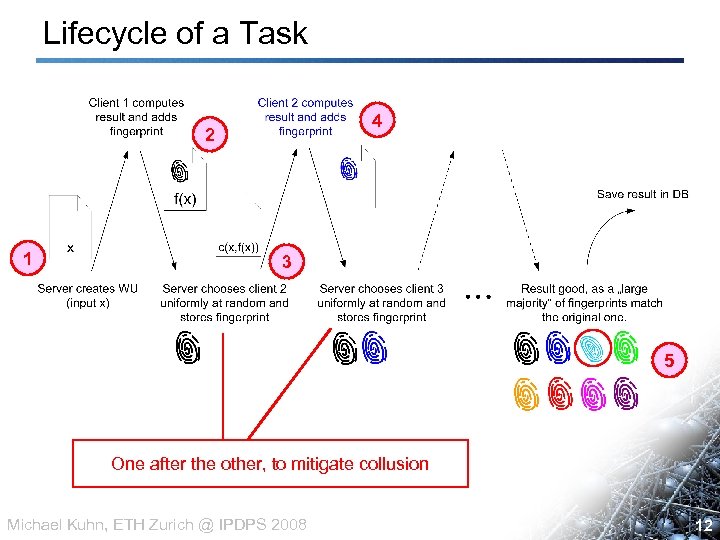
Lifecycle of a Task 4 2 1 3 5 One after the other, to mitigate collusion Michael Kuhn, ETH Zurich @ IPDPS 2008 12 12

Preventing Sybil Attacks • Problem: Zero cost identity – Solution: Don‘t assign identity for free! • Idea: Couple p (#clients) to q (computing resources) – New client has to perform some work without getting credits => buys identity – Goal: make the number of incorrect results a cheater can deliver before being detected lower than the price to buy the identity – Observe: For honest participants the price is low (as they only have to „pay“ once) Michael Kuhn, ETH Zurich @ IPDPS 2008 13 13
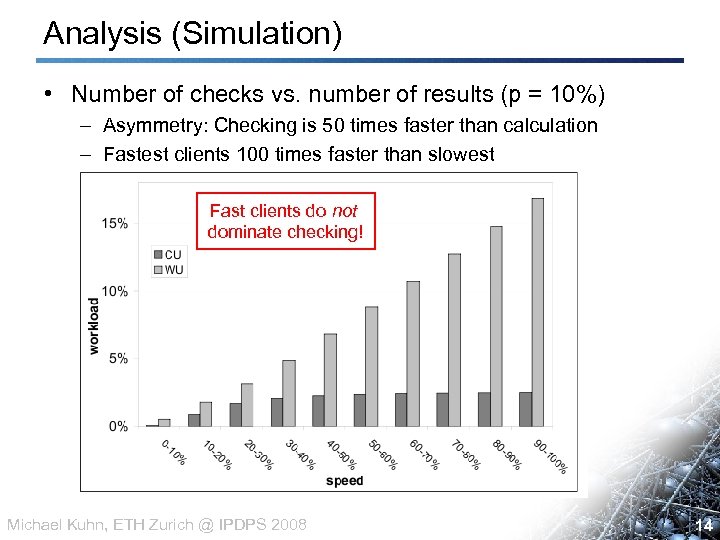
Analysis (Simulation) • Number of checks vs. number of results (p = 10%) – Asymmetry: Checking is 50 times faster than calculation – Fastest clients 100 times faster than slowest Fast clients do not dominate checking! Michael Kuhn, ETH Zurich @ IPDPS 2008 14 14
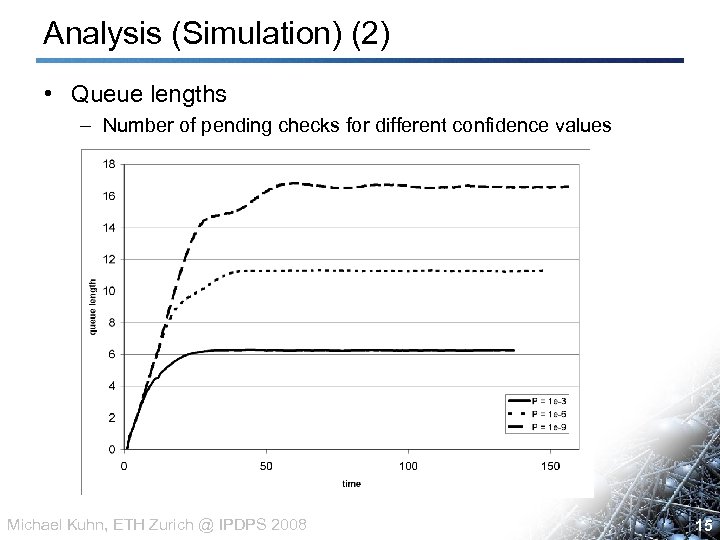
Analysis (Simulation) (2) • Queue lengths – Number of pending checks for different confidence values Michael Kuhn, ETH Zurich @ IPDPS 2008 15 15
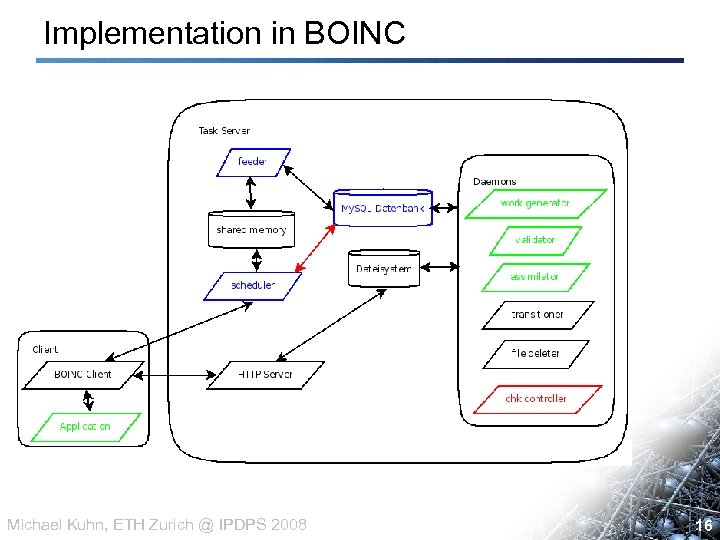
Implementation in BOINC Michael Kuhn, ETH Zurich @ IPDPS 2008 16 16

ECC Challenge • Task: Break large discrete logarithm on elliptic curve – Currently: 130 -bit – Reward: 20, 000 USD • Discrete Logarithm – Given a group with generator g, as well as a group element h: Find x, such that g^x = h • Best known algorithm: Pollard-Rho – Well suited for parallelization and use in grids Michael Kuhn, ETH Zurich @ IPDPS 2008 17 17
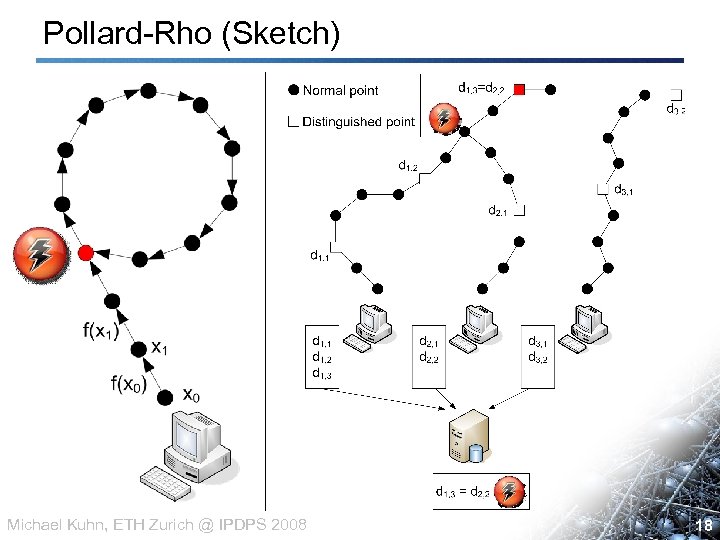
Pollard-Rho (Sketch) Michael Kuhn, ETH Zurich @ IPDPS 2008 18 18
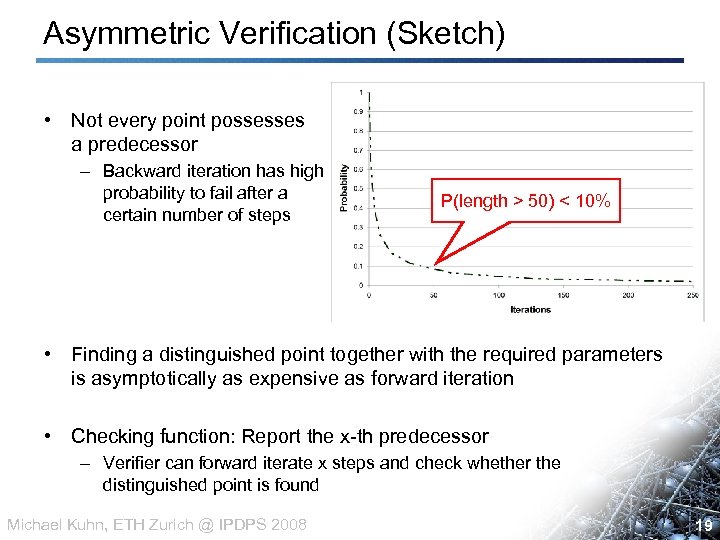
Asymmetric Verification (Sketch) • Not every point possesses a predecessor – Backward iteration has high probability to fail after a certain number of steps P(length > 50) < 10% • Finding a distinguished point together with the required parameters is asymptotically as expensive as forward iteration • Checking function: Report the x-th predecessor – Verifier can forward iterate x steps and check whether the distinguished point is found Michael Kuhn, ETH Zurich @ IPDPS 2008 19 19

Conclusions • Algorithm for distributed verification in volunteer computing, which is resistant against: – Seemingly fast clients (uniform selection of verifier among all active clients) – Lazy checking (fingerprint property) – Replay attacks (uniqueness property) – Sybil attacks (don‘t assign identity for free) • Downside: Strong assumption on the verification function – But: such verification functions exist (Pollard-Rho) • Future: More generic approaches Michael Kuhn, ETH Zurich @ IPDPS 2008 20 20

Thanks for your Interest • Questions? Michael Kuhn, ETH Zurich @ IPDPS 2008 21 21
09c88f1547ffdaaea1fe5e33f0e350ea.ppt