3d1776849eabf8db2c78638956c8f574.ppt
- Количество слайдов: 40

Distinction Between Entanglement and Coherence in Many Photon States and Impact on Super. Resolution Jonathan P. Dowling Hearne Institute for Theoretical Physics Quantum Science and Technologies Group Louisiana State University Baton Rouge, Louisiana USA quantum. phys. lsu. edu ONR SCE Program Review San Diego, 28 JAN 13

Outline 1. Super-Resolution vs. Super-Sensitivity 2. High N 00 N States of Light 3. Efficient N 00 N Generators 4. The Role of Photon Loss 5. Mitigating Photon Loss with M&M States 6. Super-Resolving Detection with Coherent States 7. Super-Resolving Radar Ranging at Shotnoise

Quantum Metrology H. Lee, P. Kok, JPD, J Mod Opt 49, (2002) 2325 Shot noise Heisenberg

Sub-Shot-Noise Interferometric Measurements With Two-Photon N 00 N States A Kuzmich and L Mandel; Quantum Semiclass. Opt. 10 (1998) 493– 500. SNL HL

AN Boto, DS Abrams, CP Williams, JPD, PRL 85 (2000) 2733 Super-Resolution a† N a N Sub-Rayleigh
New York Times Discovery Could Mean Faster Computer Chips
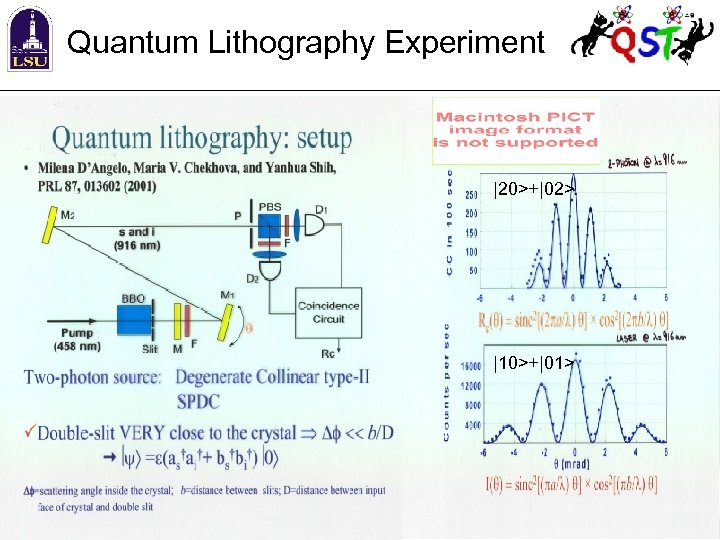
Quantum Lithography Experiment |20>+|02> |10>+|01>

Canonical Metrology Suppose we have an ensemble of N states | = (|0 + ei |1 )/ 2, and we measure the following observable: A = |0 1| + |1 0| The expectation value is given by: |A| = N cos and the variance ( A)2 is given by: N(1 cos 2 ) The unknown phase can be estimated with accuracy: A 1 = = | d A /d | N This is the standard shot-noise limit. note the square-root P Kok, SL Braunstein, and JP Dowling, Journal of Optics B 6, (2004) S 811

Quantum Lithography & Metrology Now we consider the state and we measure AN 1 H = = | d AN /d | N Quantum Metrology: N |AN| N = cos N Quantum Lithography*: High-Frequency Lithography Effect Heisenberg Limit: No Square Root! P. Kok, H. Lee, and J. P. Dowling, Phys. Rev. A 65, 052104 (2002).

Super-Sensitivity: Beats Shotnoise d. PN/d d. P 1/d N=1 (classical) N=5 (N 00 N)

Super-Resolution: Beat Rayleigh Limit N=1 (classical) N=5 (N 00 N)

Showdown at High-N 00 N! How do we make High-N 00 N!? |N, 0 + |0, N With a large cross-Kerr nonlinearity!* H = a†a b†b |1 |0 |N |N, 0 + |0, N |0 This is not practical! — need = p but = 10– 22 ! N 00 N States In Chapter 11 *C Gerry, and RA Campos, Phys. Rev. A 64, 063814 (2001).
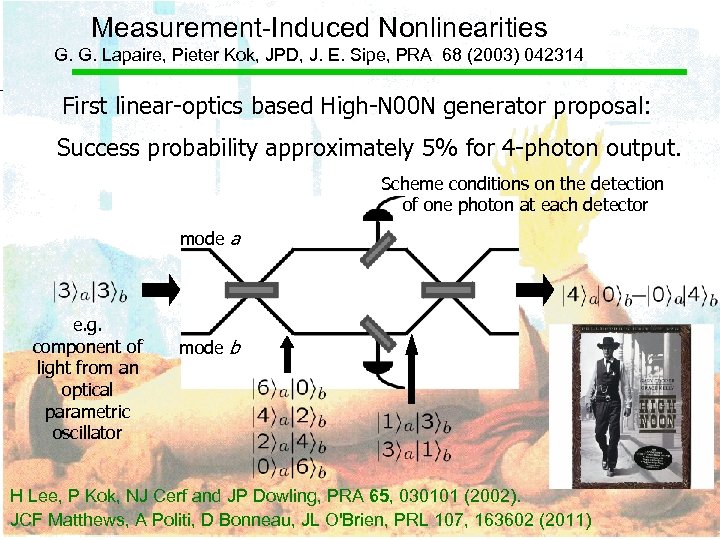
Measurement-Induced Nonlinearities G. G. Lapaire, Pieter Kok, JPD, J. E. Sipe, PRA 68 (2003) 042314 First linear-optics based High-N 00 N generator proposal: Success probability approximately 5% for 4 -photon output. Scheme conditions on the detection of one photon at each detector mode a e. g. component of light from an optical parametric oscillator mode b H Lee, P Kok, NJ Cerf and JP Dowling, PRA 65, 030101 (2002). JCF Matthews, A Politi, D Bonneau, JL O'Brien, PRL 107, 163602 (2011)
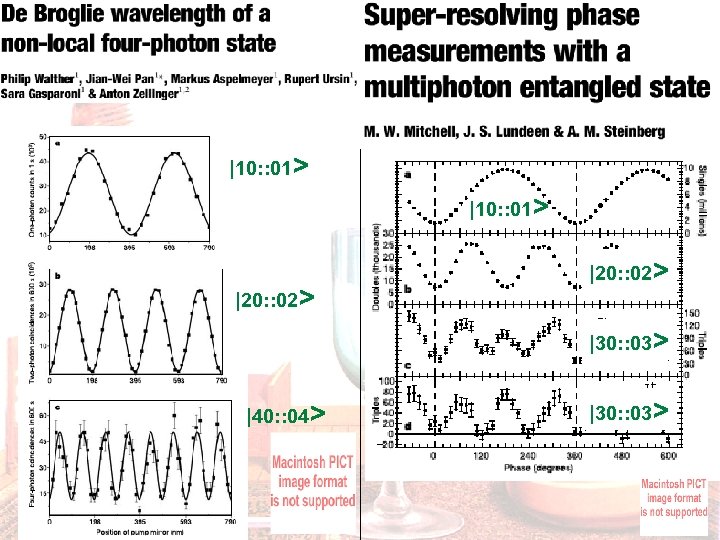
|10: : 01> |20: : 02> |30: : 03> |40: : 04> |30: : 03>
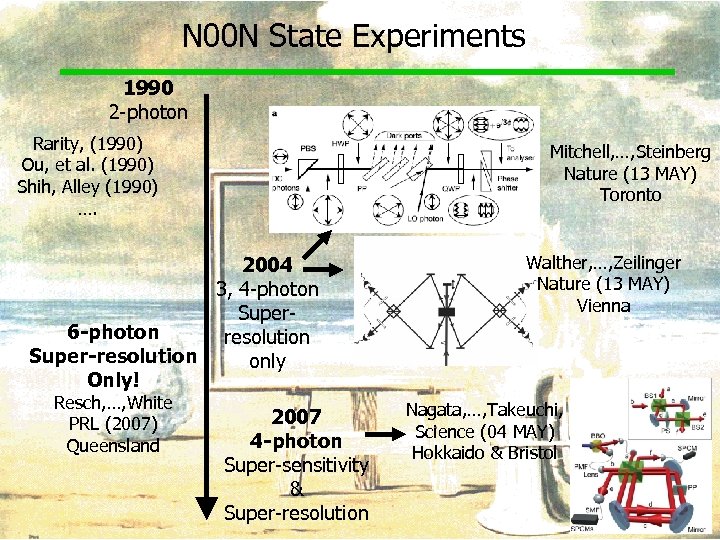
N 00 N State Experiments 1990 2 -photon Rarity, (1990) Ou, et al. (1990) Shih, Alley (1990) …. Mitchell, …, Steinberg Nature (13 MAY) Toronto 2004 3, 4 -photon Super 6 -photon resolution Super-resolution only Only! Resch, …, White PRL (2007) Queensland 2007 4 -photon Super-sensitivity & Super-resolution Walther, …, Zeilinger Nature (13 MAY) Vienna Nagata, …, Takeuchi, Science (04 MAY) Hokkaido & Bristol
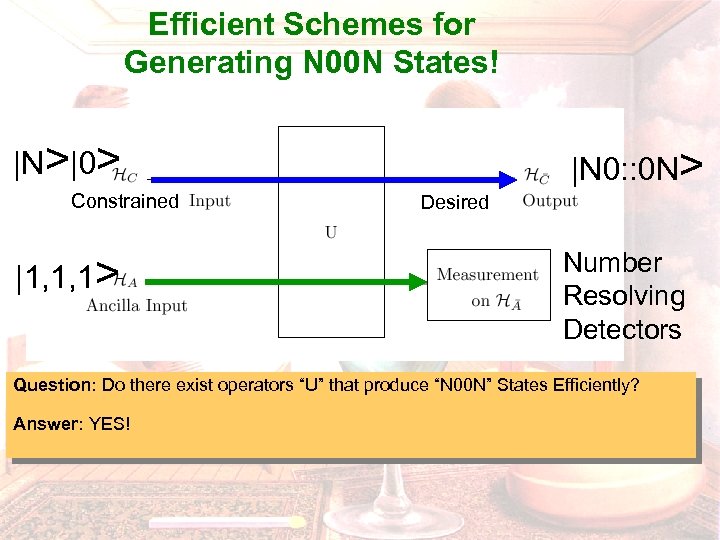
Efficient Schemes for Generating N 00 N States! |N>|0> Constrained |1, 1, 1> |N 0: : 0 N> Desired Number Resolving Detectors Question: Do there exist operators “U” that produce “N 00 N” States Efficiently? Answer: YES!

Phys. Rev. Lett. 99, 163604 (2007)

Linear Optical N 00 N Generator II U This example disproves the N 00 N Conjecture: “That it Takes At Least N Modes to Make N 00 N. ” The upper bound on the resources scales quadratically! Upper bound theorem: The maximal size of a N 00 N state generated in m modes via single photon detection in m-2 modes is O(m 2).

HIGH FLUX 2 -PHOTON NOON STATES From a High-Gain OPA (Theory) We present a theoretical analysis of the properties of an unseeded optical parametric amplifier (OPA) used as the source of entangled photons. OPA Scheme The idea is to take known bright sources of entangled photons coupled to number resolving detectors and see if this can be used in LOQC, while we wait for the single photon sources. G. S. Agarwal, et al. , J. Opt. Soc. Am. B 24, 270 (2007).

Quantum States of Light From a High-Gain OPA (Experiment) HIGH FLUX 2 PHOTON N 00 N EXPERIMENT State Before Projection Visibility Saturates at 20% with 105 Counts Per Second! F. Sciarrino, et al. , Phys. Rev. A 77, 012324 (2008)
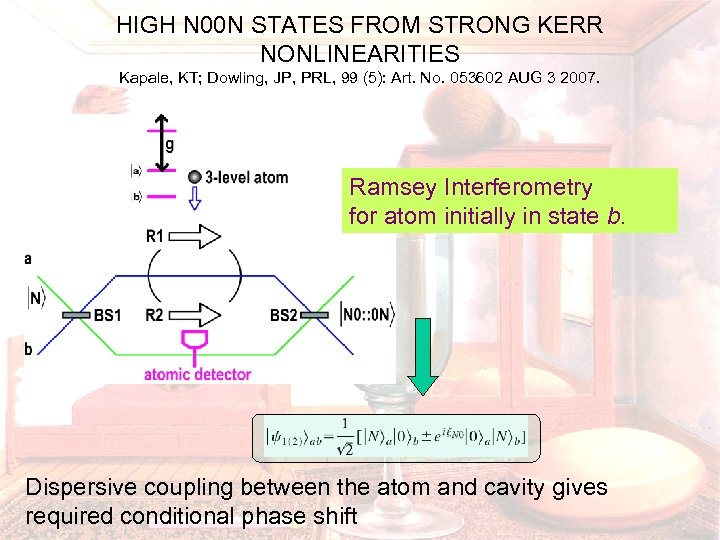
HIGH N 00 N STATES FROM STRONG KERR NONLINEARITIES Kapale, KT; Dowling, JP, PRL, 99 (5): Art. No. 053602 AUG 3 2007. Ramsey Interferometry for atom initially in state b. Dispersive coupling between the atom and cavity gives required conditional phase shift

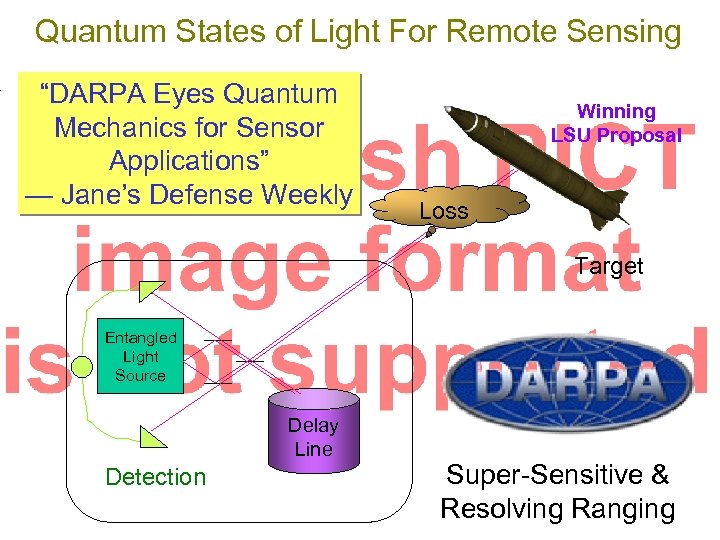
Quantum States of Light For Remote Sensing “DARPA Eyes Quantum Mechanics for Sensor Applications” — Jane’s Defense Weekly Winning LSU Proposal Loss Target Entangled Light Source Delay Line Detection Super-Sensitive & Resolving Ranging
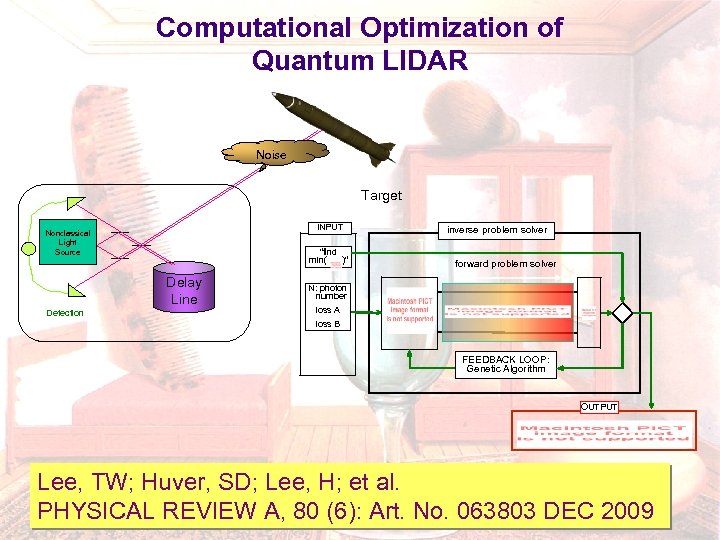
Computational Optimization of Quantum LIDAR Noise Target INPUT Nonclassical Light Source “find min( )“ Delay Line Detection inverse problem solver forward problem solver N: photon number loss A loss B FEEDBACK LOOP: Genetic Algorithm OUTPUT Lee, TW; Huver, SD; Lee, H; et al. PHYSICAL REVIEW A, 80 (6): Art. No. 063803 DEC 2009
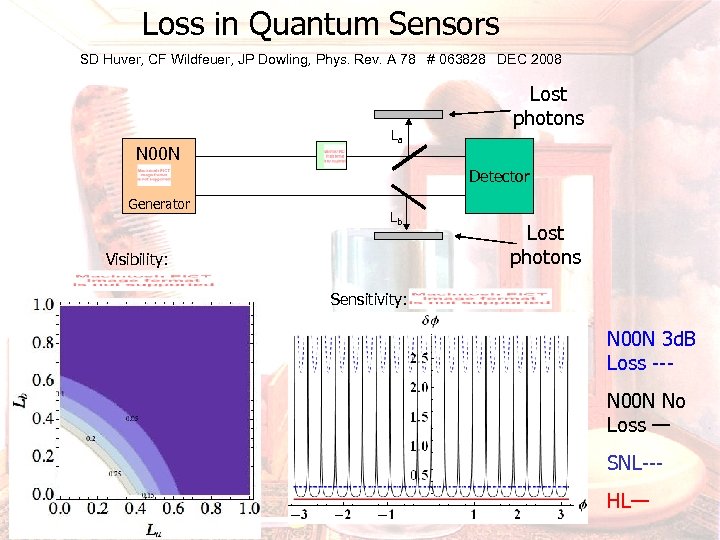
Loss in Quantum Sensors SD Huver, CF Wildfeuer, JP Dowling, Phys. Rev. A 78 # 063828 DEC 2008 N 00 N La Lost photons Detector Generator Lb Visibility: Lost photons Sensitivity: N 00 N 3 d. B Loss --N 00 N No Loss — SNL--3/19/2018 25 HL—

Super-Lossitivity Gilbert, G; Hamrick, M; Weinstein, YS; JOSA B 25 (8): 1336 -1340 AUG 2008 N=1 (classical) N=5 (N 00 N) 3 d. B Loss, Visibility & Slope — Super Beer’s Law!
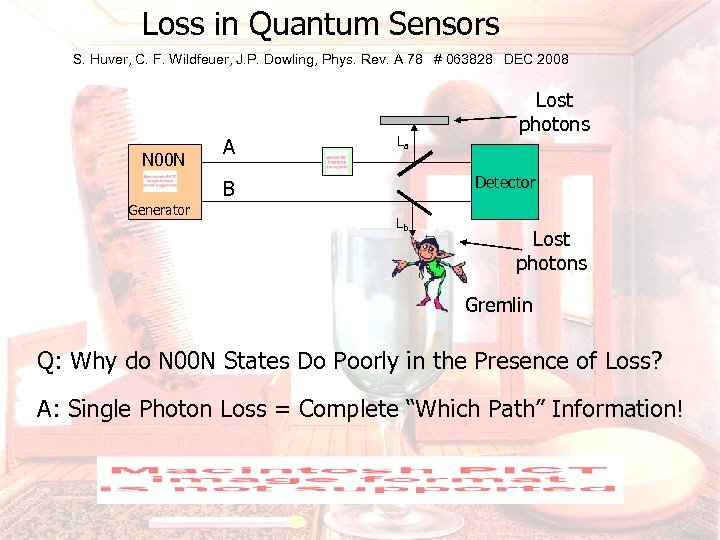
Loss in Quantum Sensors S. Huver, C. F. Wildfeuer, J. P. Dowling, Phys. Rev. A 78 # 063828 DEC 2008 N 00 N A La Detector B Generator Lost photons Lb Lost photons Gremlin Q: Why do N 00 N States Do Poorly in the Presence of Loss? A: Single Photon Loss = Complete “Which Path” Information!
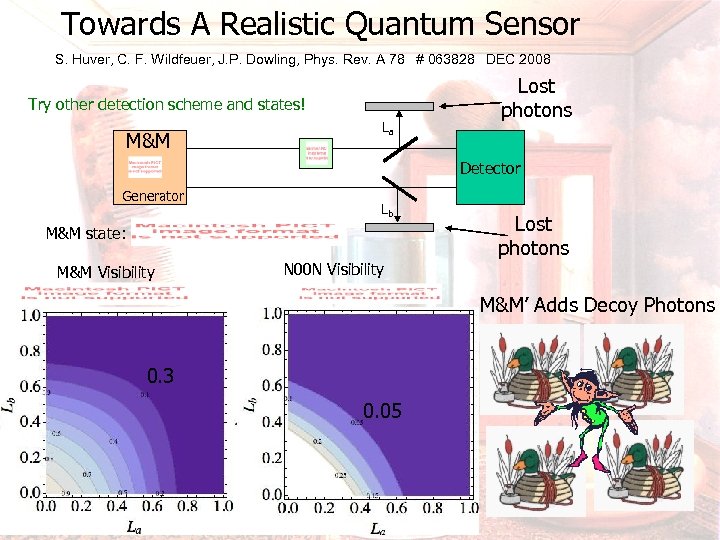
Towards A Realistic Quantum Sensor S. Huver, C. F. Wildfeuer, J. P. Dowling, Phys. Rev. A 78 # 063828 DEC 2008 Try other detection scheme and states! M&M La Lost photons Detector Generator Lb M&M state: M&M Visibility N 00 N Visibility Lost photons M&M’ Adds Decoy Photons 0. 3 0. 05
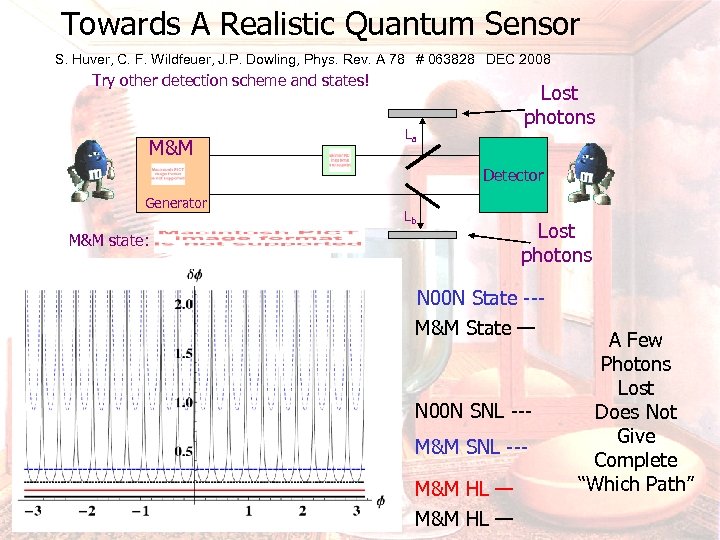
Towards A Realistic Quantum Sensor S. Huver, C. F. Wildfeuer, J. P. Dowling, Phys. Rev. A 78 # 063828 DEC 2008 Try other detection scheme and states! M&M Lost photons La Detector Generator Lb M&M state: Lost photons N 00 N State --M&M State — N 00 N SNL --M&M HL — A Few Photons Lost Does Not Give Complete “Which Path”

Optimization of Quantum Interferometric Metrological Sensors In the Presence of Photon Loss PHYSICAL REVIEW A, 80 (6): Art. No. 063803 DEC 2009 Tae-Woo Lee, Sean D. Huver, Hwang Lee, Lev Kaplan, Steven B. Mc. Cracken, Changjun Min, Dmitry B. Uskov, Christoph F. Wildfeuer, Georgios Veronis, Jonathan P. Dowling We optimize two-mode, entangled, number states of light in the presence of loss in order to maximize the extraction of the available phase information in an interferometer. Our approach optimizes over the entire available input Hilbert space with no constraints, other than fixed total initial photon number. INPUT “find min( )“ inverse problem solver forward problem solver N: photon number loss A loss B FEEDBACK LOOP: Genetic Algorithm OUTPUT
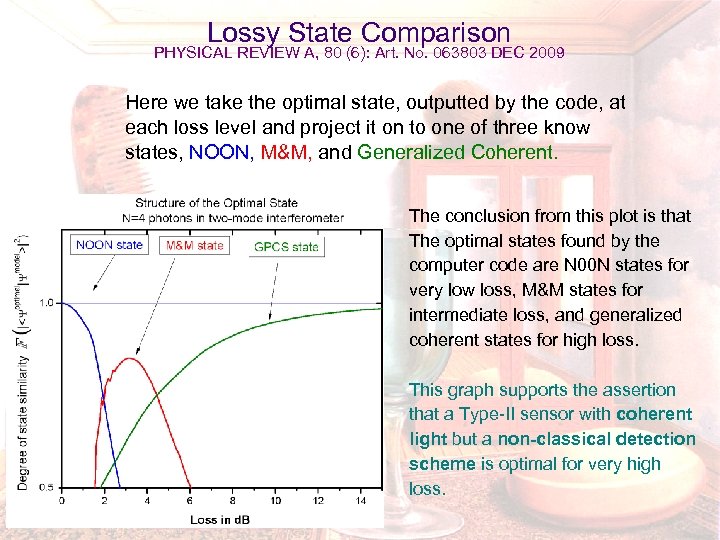
Lossy State Comparison PHYSICAL REVIEW A, 80 (6): Art. No. 063803 DEC 2009 Here we take the optimal state, outputted by the code, at each loss level and project it on to one of three know states, NOON, M&M, and Generalized Coherent. The conclusion from this plot is that The optimal states found by the computer code are N 00 N states for very low loss, M&M states for intermediate loss, and generalized coherent states for high loss. This graph supports the assertion that a Type-II sensor with coherent light but a non-classical detection scheme is optimal for very high loss.

Super-Resolution at the Shot-Noise Limit with Coherent States and Photon-Number-Resolving Detectors JOURNAL OF THE OPTICAL SOCIETY OF AMERICA B-OPTICAL PHYSICS 27 (6): A 170 -A 174 Yang Gao, Christoph F. Wildfeuer, Petr M. Anisimov, Hwang Lee, Jonathan P. Dowling We show that coherent light coupled with a quantum detection scheme — parity measurement! — can provide a super-resolution much below the Rayleigh diffraction limit, with sensitivity at the shot-noise limit in terms of the detected photon power. Parity Measurement! Quantum Classical Quantum Detector! Waves are Coherent!

WHY? THERE’S N 0 ON IN THEM-THERE HILLS!

Super-Resolution at the Shot-Noise Limit with Coherent States and Photon-Number-Resolving Detectors JOURNAL OF THE OPTICAL SOCIETY OF AMERICA B-OPTICAL PHYSICS 27 (6): A 170 -A 174 Yang Gao, Christoph F. Wildfeuer, Petr M. Anisimov, Hwang Lee, Jonathan P. Dowling

For coherent states parity detection can be implemented with a “quantum inspired” homodyne detection scheme.

Super Resolution with Classical Light at the Quantum Limit Emanuele Distante, Miroslav Jezek, and Ulrik L. Andersen
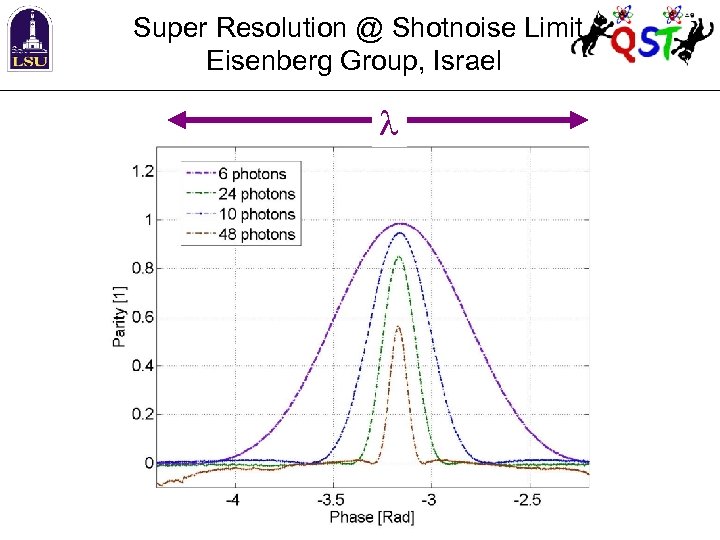
Super Resolution @ Shotnoise Limit Eisenberg Group, Israel
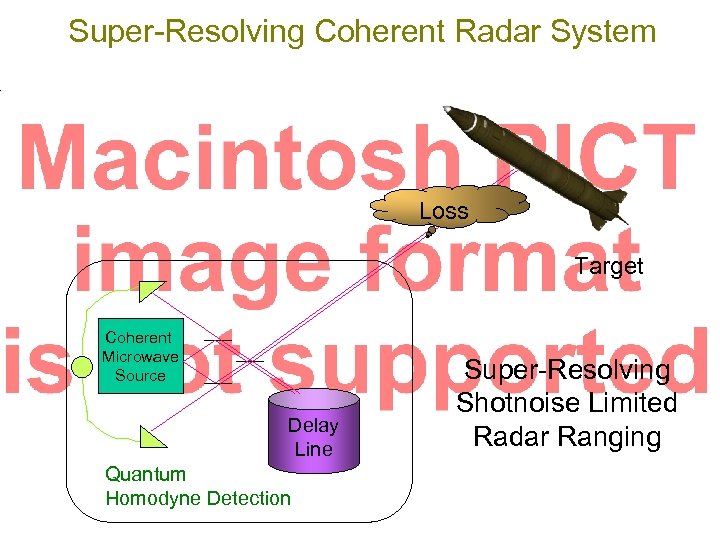
Super-Resolving Coherent Radar System Loss Target Coherent Microwave Source Delay Line Quantum Homodyne Detection Super-Resolving Shotnoise Limited Radar Ranging

Super-Resolving Quantum Radar Objective • Coherent Radar at Low Power • Sub-Rayleigh Resolution Ranging • Operates at Shotnoise Limit Objective Approach • RADAR with Super Resolution Status • Confirmed Super-resolution • Proof-of-Principle in Visible & IR • Standard RADAR Source • Loss Analysis in Microwave Needed • Quantum Detection Scheme • Atmospheric Modelling Needed

Outline 1. Super-Resolution vs. Super-Sensitivity 2. High N 00 N States of Light 3. Efficient N 00 N Generators 4. The Role of Photon Loss 5. Mitigating Photon Loss with M&M States 6. Super-Resolving Detection with Coherent States 7. Super-Resolving Radar Ranging at Shotnoise
3d1776849eabf8db2c78638956c8f574.ppt