ДИСПЕРСИОННЫЙ АНАЛИЗ

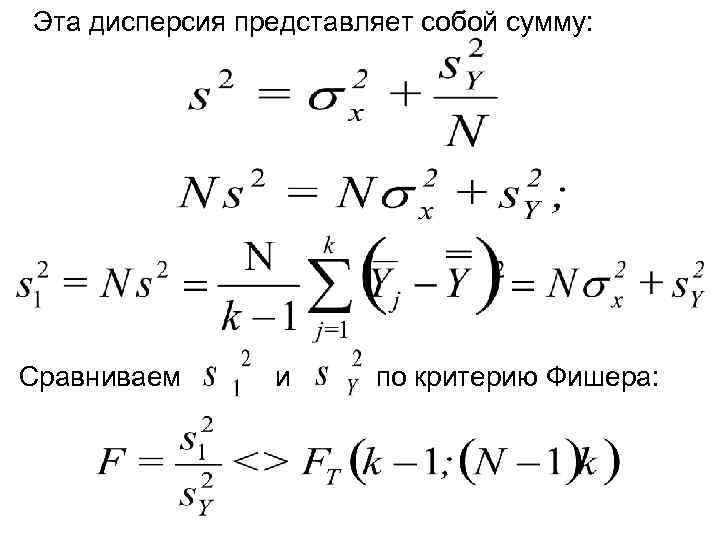
ДИСПЕРСИОННЫЙ АНАЛИЗ Цель дисперсионного анализа – установить, влияют ли факторы группы Х на функцию цели Y в условиях действия факторов W и заданных факторах группы Z. Вспомним: Цель регрессионного анализа – установить, как факторы группы Х влияют на функцию цели Y в условиях действии факторов W и заданных факторах группы Z.

Достаточно часто перед исследователем стоит задача установления самого факта влияния фактора Х на функцию цели Y, а не оценки характера этого влияния. Установив надежно и достоверно факт влияния, исследователь может принять меры к устранению этого влияния, а не тратить время на поиск зависимости Y от Х.

1 случай: фактор Х — один (однофакторный дисперсионный анализ) и заранее оценено влияние случайных факторов. Функция цели Y условно представляется в виде 2 -х составляющих: Y' — составляющая, зависящая от Х, но не подверженная влиянию случайных факторов W; Y'' — составляющая, не зависящая от Х, но подверженная влиянию случайных факторов W.

Для оценки разброса Y'' служит дисперсия Введем условную величину, аналогичную дисперсии, для Y': где - среднее значение Y'; k — число уровней фактора Х; i — текущий номер уровня; оценивает меру влияния Х на Y.

Дисперсия наблюдения величины Y - в соответствии со свойствами дисперсии вычисляется как Сравним по критерию Фишера на уровне значимости q дисперсии и :

Если то дисперсии и отличаются незначимо, т. е. являются однородными. Это означает, что , то есть фактор X не влияет на функцию цели Y на фоне действия случайных факторов. Если то дисперсии и являются неоднородными, т. е. отличаются значимо. Это означает, что , то есть на фоне действия случайных факторов проявляется влияние фактора X на Y.

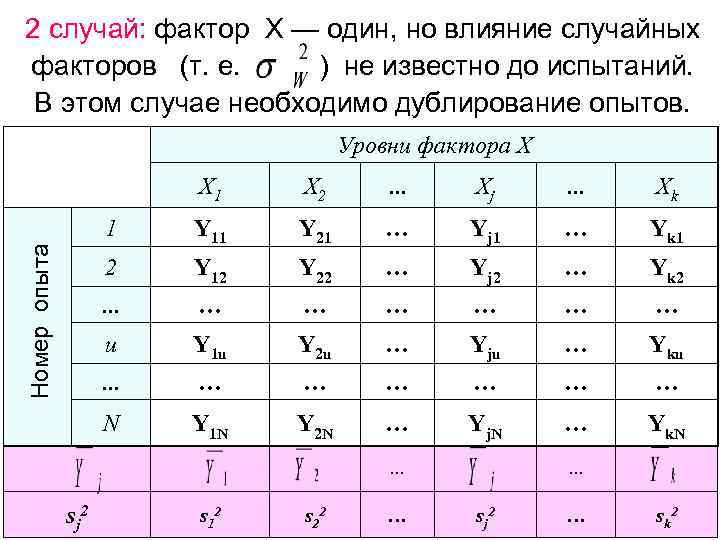
2 случай: фактор Х — один, но влияние случайных факторов (т. е. ) не известно до испытаний. В этом случае необходимо дублирование опытов. Уровни фактора Х X 1 X 2 … Xj … Xk 1 Y 11 Y 21 … Yj 1 … Yk 1 Номер опыта 2 Y 12 Y 22 … Yj 2 … Yk 2 … … … … u Y 1 u Y 2 u … Yju … Yku … … … … N Y 1 N Y 2 N … Yj. N … Yk. N … sj 2 s 1 2 s 2 2 … sj 2 … sk 2

Среднее значение Y и дисперсия в каждом столбце рассчитываются по формулам: Число степеней свободы для дисперсии : Проверяем дисперсии на однородность по критерию Кохрена.

Если дисперсии неоднородны, то строгий дисперсионный анализ невозможен, и неоднородность дисперсий надо устранять. Если дисперсии однородны , то оценкой генеральной дисперсии, отражающей влияние случайных факторов будет дисперсия определенная с числом степеней свободы

Если фактор X влияет на функцию цели Y, то это можно выявить, сравнивая средние по столбцам величины . Рассчитаем дисперсию s 2 по строке средних значений таблицы Среднее средних

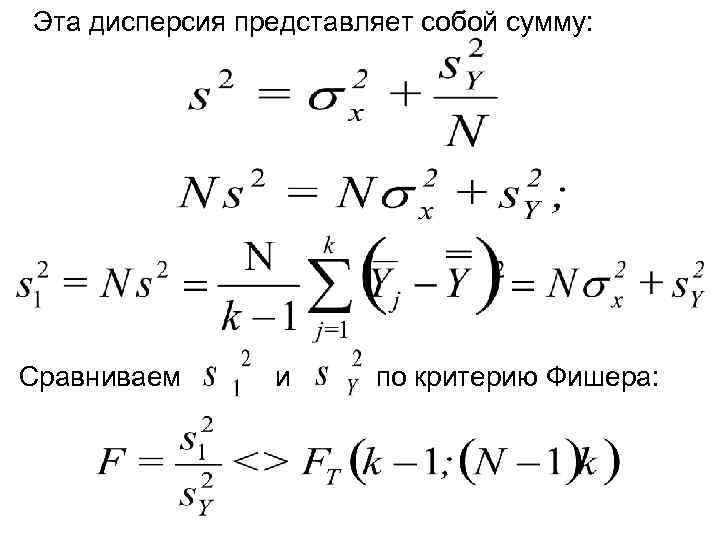Эта дисперсия представляет собой сумму: Сравниваем и по критерию Фишера:

Если то уровень фактора X не влияет на функцию цели Y на фоне действия случайных факторов. Если то при выбранном уровне значимости на фоне действия случайных факторов имеется влияние фактора X на Y.

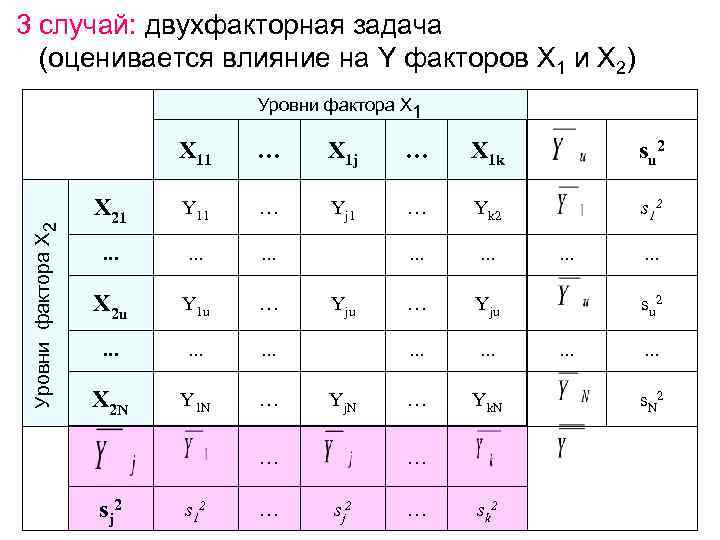
3 случай: двухфакторная задача (оценивается влияние на Y факторов X 1 и X 2) Уровни фактора Х 1 X 11 … X 1 j … X 1 k s u 2 X 21 Y 11 … Yj 1 … Yk 2 s 1 2 Уровни фактора Х 2 … … … … … X 2 u Y 1 u … Yju … Yju su 2 … … … … … X 2 N Y 1 N … Yj. N … Yk. N s. N 2 … s j 2 s 1 2 … sj 2 … sk 2

Дисперсии по столбцам ( S j 2 ) и строкам ( рассчитывают в том случае, если заранее не оценено влияние случайных факторов. Если дисперсия определена предварительно, то по таблице рассчитывают только дисперсии с числом степеней свободы

Факт влияния на функцию цели Y фактора X 1 устанавливают по критерию Фишера, сравнивая дисперсии и Факт влияния на функцию цели Y фактора X 2 устанавливают по критерию Фишера, сравнивая дисперсии и

ДИСПЕРСИОННЫЙ АНАЛИЗ В УСЛОВИЯХ НЕОДНОРОДНОСТИ Неоднородность – это влияние, которое существует, но не представляет интереса для исследователя. Влияние неоднородностей необходимо исключать. Пример: В процессе эксперимента необходимо установить факт влияния на производительность (Y) нового металлорежущего станка двух факторов: типа режущего инструмента (X 1) и варианта настройки регуляторов ЭП (X 2). Эксперимент проводится на четырех станках, при этом исследуется четыре типа инструмента и четыре варианта настройки привода.

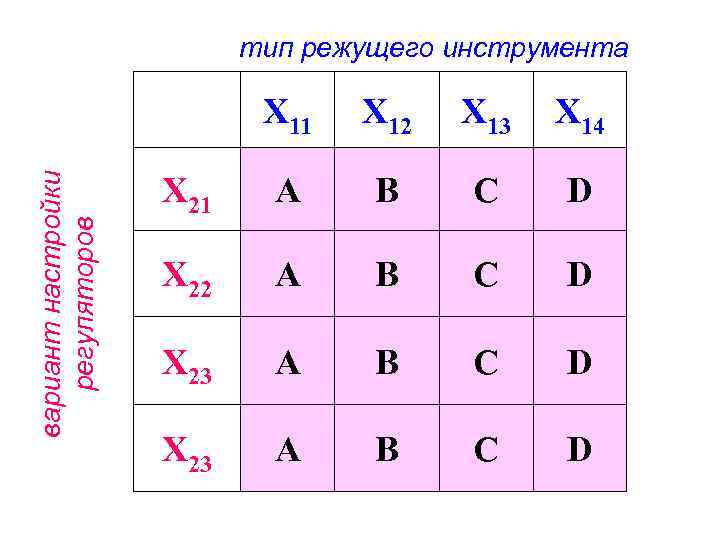
Составим план эксперимента: тип режущего инструмента X 11 X 12 X 13 X 14 X 21 A A вариант настройки регуляторов X 22 B B X 23 C C X 23 D D

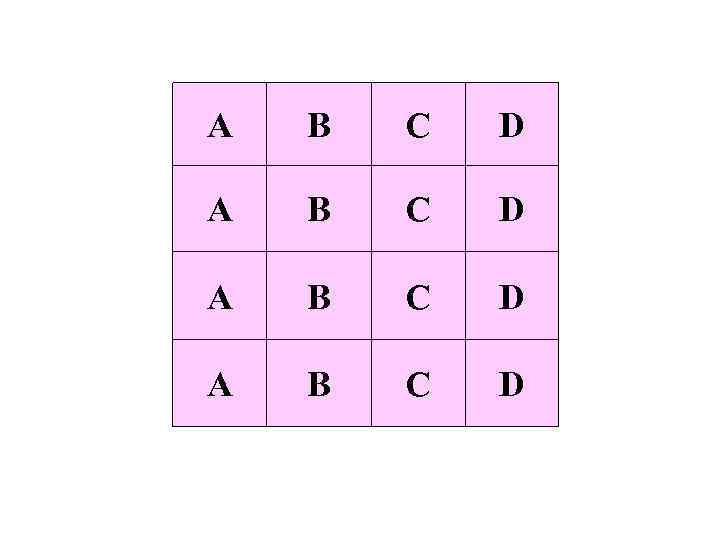
тип режущего инструмента X 11 X 12 X 13 X 14 X 21 A B C D вариант настройки регуляторов X 22 A B C D X 23 A B C D

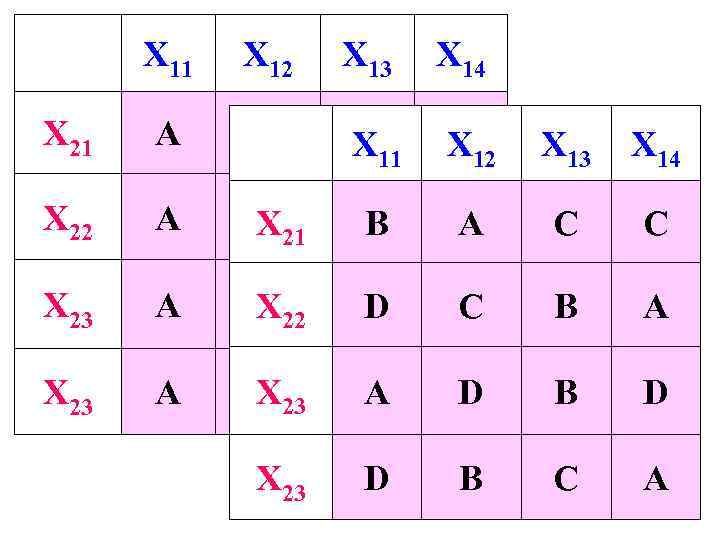
X 11 X 12 X 13 X 14 X 21 A B C X 11 D X 12 X 13 X 14 X 22 A B 21 X C B D A C C X 23 A B 22 X C D D C B A X 23 A X B 23 A C D D B D X 23 D B C A

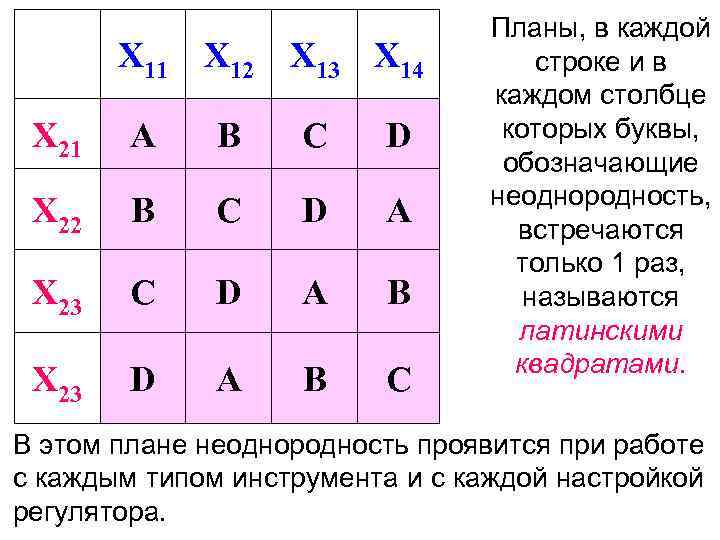
Планы, в каждой X 11 X 12 X 13 X 14 строке и в каждом столбце X 21 A B C D которых буквы, обозначающие неоднородность, X 22 B C D A встречаются только 1 раз, X 23 C D A B называются латинскими квадратами. X 23 D A B C В этом плане неоднородность проявится при работе с каждым типом инструмента и с каждой настройкой регулятора.

На практике может существовать не только одна неоднородность. Например, может также влиять квалификация оператора станка или его личные качества. Планы, позволяющие устранить две неоднородности, строятся по принципу греко-латинских квадратов. Aα Bβ Cγ Cβ Aγ Bα Bγ Cα Aβ

A B C D