ДИСКРЕТНАЯ МАТЕМАТИКА ТЕОРИЯ МНОЖЕСТВ УПОРЯДОЧЕННЫЕ МНОЖЕСТВА. ОТНОШЕНИЕ ПОРЯДКА

ДИСКРЕТНАЯ МАТЕМАТИКА ТЕОРИЯ МНОЖЕСТВ УПОРЯДОЧЕННЫЕ МНОЖЕСТВА. ОТНОШЕНИЕ ПОРЯДКА лекция 5 Факультет компьютерной инженерии и управления, кафедра АПВТ, ХНУРЭ Лектор – д. т. н. , проф. Хаханов В. И. Харьковский национальный университет радиоэлектроники, кафедра АПВТ, тел. 7021 326, е-mail: ri@kture. kharkov. ua 1

Упорядоченные множества. Отношение порядка Тема: Упорядоченные множества. Отношение порядка 2011 Цель лекции – изучить свойства упорядоченных множеств и отношения порядка для применения в задачах компьютерной инженерии Содержание: • Определение бинарного отношения порядка • Упорядоченные множества • Линейный и частичный порядок • Диаграммы Хассе • Старший элемент, мажоранта, миноранта • Обратное отношение. Принцип двойственности ХНУРЭ, факультет КИУ, кафедра АПВТ, тел. 7021 326, e-mail: ri@kture. kharkov. ua 2

Упорядоченные множества. Отношение порядка 2011 Литература • Горбатов В. А. Основы дискретной математики. М. : Высш. шк. , 1986. 9 -12 с. • Лавров И. А. , Максимова Л. Л. Задачи по теории множеств, математической логике и теории алгоритмов. М. : Наука. Главная редакция физико-математической литературы, 1984. 4 -10 с. • Кузнецов О. П. , Адельсон-Вельский Г. М. Дискретная математика для инженера. М. : Энергия, 1980. 344 с. • Новиков Ф. А. Дискретная математика для программистов. С. -П. , 2001. С. 4 -24. • Бондаренко М. Ф. , Белоус Н. В. , Руткас А. Г. Компьютерная дискретная математика. – Харьков: СМИТ, 2004. – 480 с. • Хаханов В. І. , Хаханова І. В. , Кулак Е. М. , Чумаченко С. В. Методичні вказівки до практичних занять з курсу “Дискретна математика”. Харків, ХНУРЕ. 2001. 17 -20 с. ХНУРЭ, факультет КИУ, кафедра АПВТ, тел. 7021 326, e-mail: ri@kture. kharkov. ua 3

Упорядоченные множества. Отношение порядка 2011 Термины Базовые понятия: множество, § подмножество, § бинарное отношение, § рефлексивность, § симметричность, § транзитивность ХНУРЭ, факультет КИУ, кафедра АПВТ, тел. 7021 326, e-mail: ri@kture. kharkov. ua Ключевые слова: § бинарное отношение порядка, § рефлексивность, § антисимметричность, § транзитивность, § старший элемент, § наибольший (наименьший) элемент, § мажоранта (миноранта), § верхняя (нижняя) грань, § супремум (инфимум) 4

Упорядоченные множества. Отношение порядка 2011 Определение отношения порядка n n n Def: бинарным отношением порядка (упорядоченности) называется рефлексивное, антисимметричное и транзитивное отношение Обозначение: R М 2 : 1. x M: x x; 2. x, y M: x y, y x x=y; 3. x, y, z M: x y, y z x z Def: упорядоченным называется множество с заданным отношением порядка (М, R ). ХНУРЭ, факультет КИУ, кафедра АПВТ, тел. 7021 326, e-mail: ri@kture. kharkov. ua Бинарное отношение порядка R = n Рефлексивность + Антисимметричность + Транзитивность 5

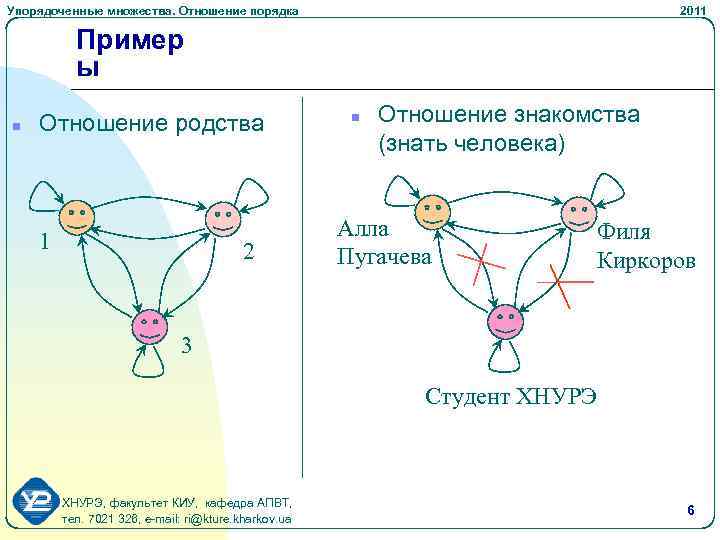Упорядоченные множества. Отношение порядка 2011 Пример ы n Отношение родства 1 2 n Отношение знакомства (знать человека) Алла Пугачева Филя Киркоров 3 Студент ХНУРЭ, факультет КИУ, кафедра АПВТ, тел. 7021 326, e-mail: ri@kture. kharkov. ua 6

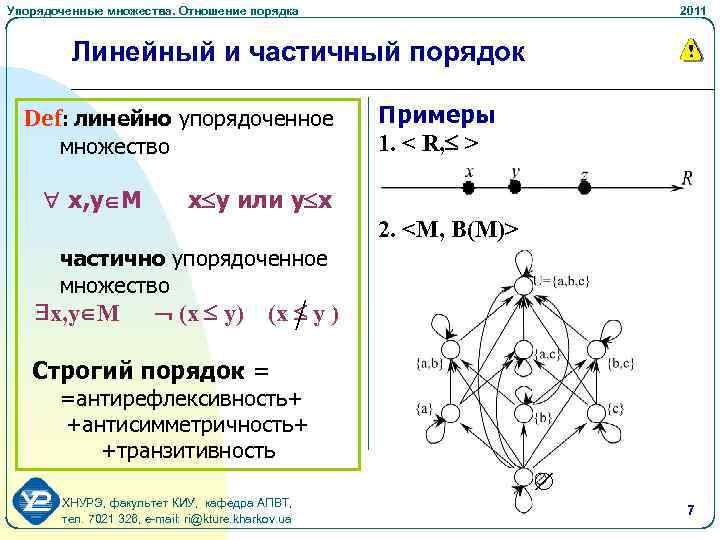Упорядоченные множества. Отношение порядка 2011 Линейный и частичный порядок Def: линейно упорядоченное множество x, y M Примеры 1. < R, > x y или y x 2. частично упорядоченное множество x, y M (x y) (x y ) Строгий порядок = =антирефлексивность+ +антисимметричность+ +транзитивность ХНУРЭ, факультет КИУ, кафедра АПВТ, тел. 7021 326, e-mail: ri@kture. kharkov. ua 7

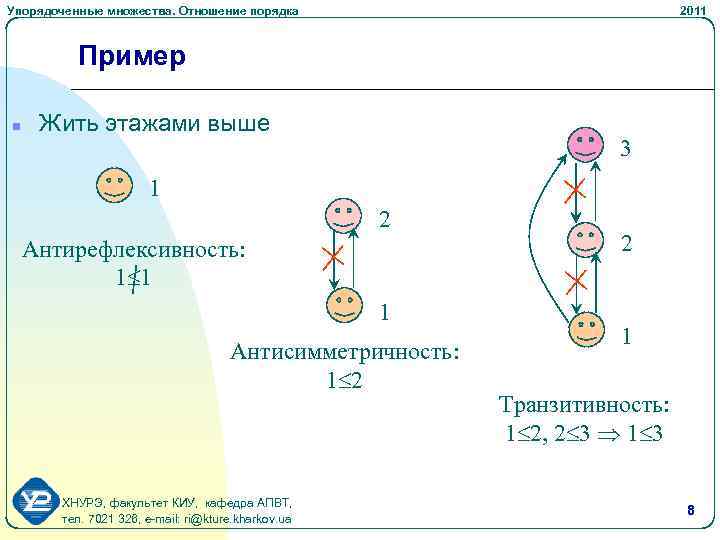Упорядоченные множества. Отношение порядка 2011 Пример n Жить этажами выше 3 1 2 Антирефлексивность: 1 1 1 Антисимметричность: 1 2 ХНУРЭ, факультет КИУ, кафедра АПВТ, тел. 7021 326, e-mail: ri@kture. kharkov. ua 2 1 Транзитивность: 1 2, 2 3 1 3 8

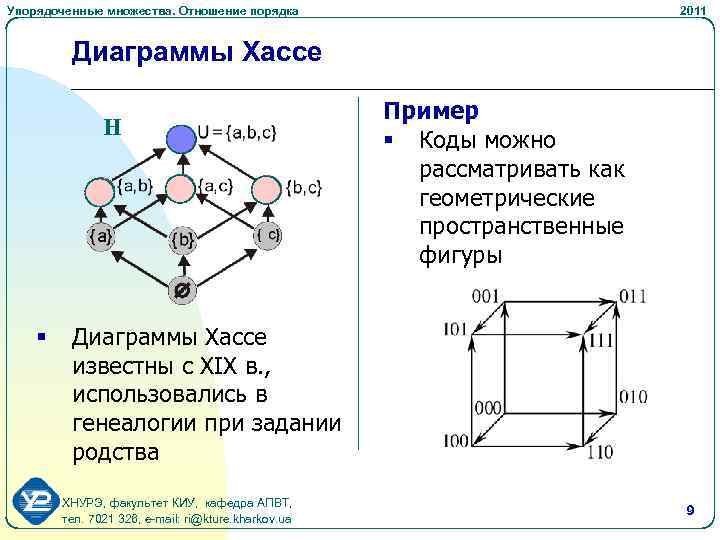Упорядоченные множества. Отношение порядка 2011 Диаграммы Хассе Н § Пример § Коды можно рассматривать как геометрические пространственные фигуры Диаграммы Хассе известны с XIX в. , использовались в генеалогии при задании родства ХНУРЭ, факультет КИУ, кафедра АПВТ, тел. 7021 326, e-mail: ri@kture. kharkov. ua 9

Упорядоченные множества. Отношение порядка 2011 Time-Out ХНУРЭ, факультет КИУ, кафедра АПВТ, тел. 7021 326, e-mail: ri@kture. kharkov. ua 10

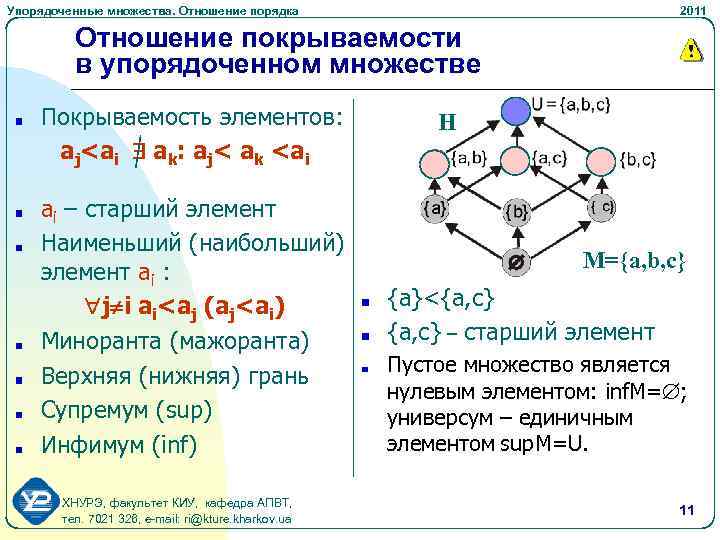Упорядоченные множества. Отношение порядка 2011 Отношение покрываемости в упорядоченном множестве Покрываемость элементов: aj

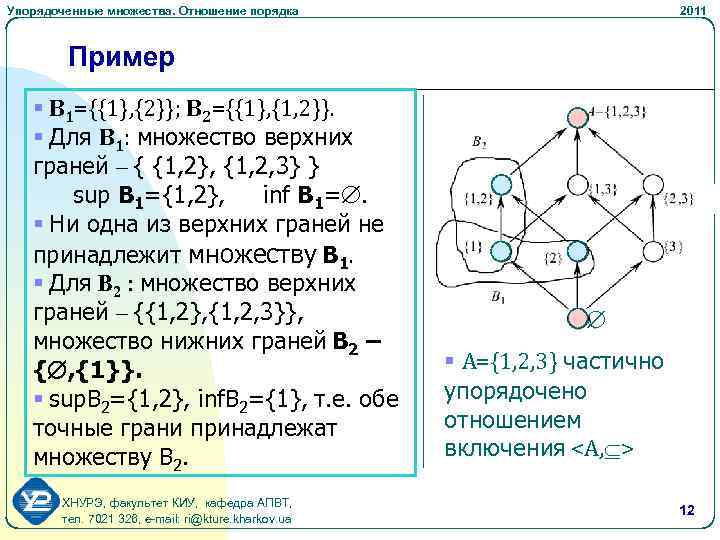Упорядоченные множества. Отношение порядка 2011 Пример § B 1={{1}, {2}}; B 2={{1}, {1, 2}}. § Для B 1: множество верхних граней – { {1, 2}, {1, 2, 3} } sup B 1={1, 2}, inf B 1=. § Ни одна из верхних граней не принадлежит множеству B 1. § Для B 2 : множество верхних граней – {{1, 2}, {1, 2, 3}}, множество нижних граней B 2 – { , {1}}. § sup. B 2={1, 2}, inf. B 2={1}, т. е. обе точные грани принадлежат множеству B 2. ХНУРЭ, факультет КИУ, кафедра АПВТ, тел. 7021 326, e-mail: ri@kture. kharkov. ua § A={1, 2, 3} частично упорядочено отношением включения 12

Упорядоченные множества. Отношение порядка 2011 Единственность наибольшего (наименьшего) элемента Def: цепь M´ M - подмножество упорядоченного множества. Длина цепи: l =| M´|-1. Def: высота элемента d(mi) упорядоченного множества M Пусть mi è mj – два – максимум длин цепей наибольших элемента, m 0

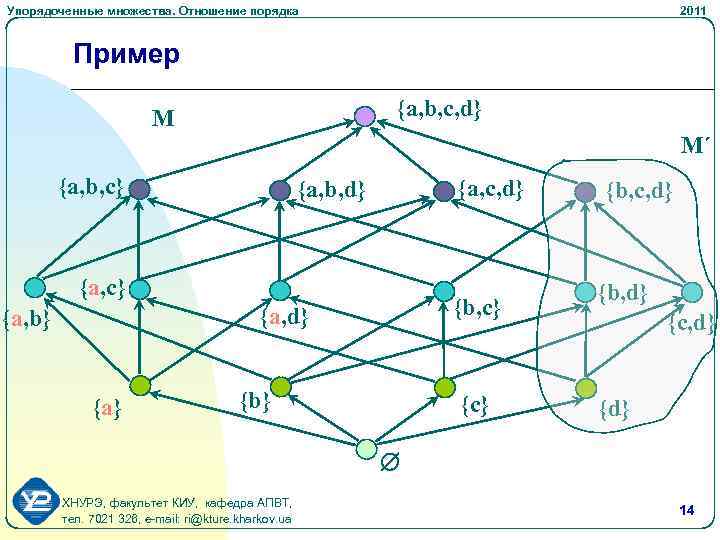Упорядоченные множества. Отношение порядка 2011 Пример {a, b, c, d} M M´ {a, b, c} {a, c, d} {a, b, d} {a, c} {b, c} {a, d} {a, b} {a} {b} {c} {b, c, d} {b, d} {c, d} {d} ХНУРЭ, факультет КИУ, кафедра АПВТ, тел. 7021 326, e-mail: ri@kture. kharkov. ua 14

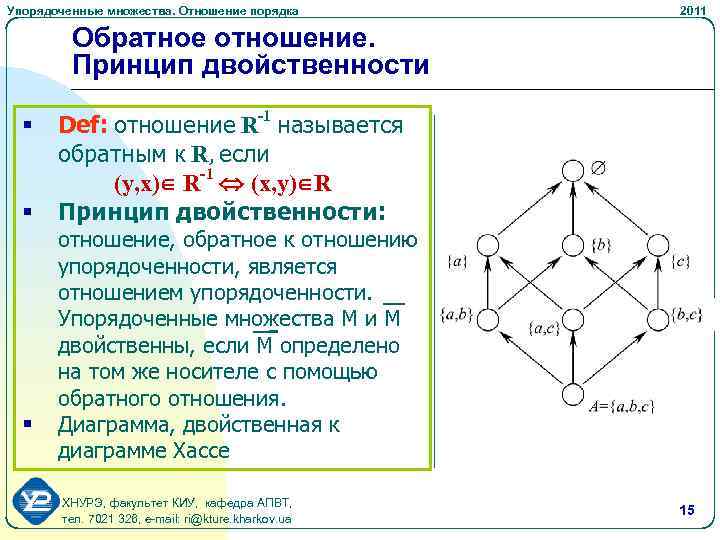Упорядоченные множества. Отношение порядка 2011 Обратное отношение. Принцип двойственности § § § Def: отношение R-1 называется обратным к R, если (y, x) R-1 (x, y) R Принцип двойственности: отношение, обратное к отношению упорядоченности, является отношением упорядоченности. Упорядоченные множества М и М двойственны, если М определено на том же носителе с помощью обратного отношения. Диаграмма, двойственная к диаграмме Хассе ХНУРЭ, факультет КИУ, кафедра АПВТ, тел. 7021 326, e-mail: ri@kture. kharkov. ua 15

Упорядоченные множества. Отношение порядка 2011 Выводы n n n Бинарное отношение порядка устанавливает на множестве отношение покрываемости, задает предшествование и старшинство элементов Упорядоченные множества являются иерархическими структурами Упорядоченные множества представляются диаграммами Хассе Коды можно рассматривать как некоторые пространственные геометрические фигуры Триаду можно представить в виде единичного куба, имеющего координаты вершин, которые отвечают двоичным символам ХНУРЭ, факультет КИУ, кафедра АПВТ, тел. 7021 326, e-mail: ri@kture. kharkov. ua 16

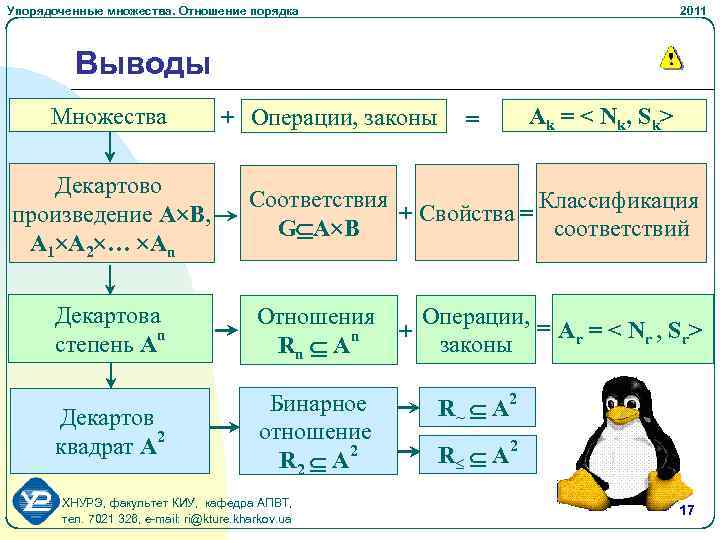Упорядоченные множества. Отношение порядка 2011 Выводы Множества Декартово произведение A B, A 1 A 2 … An + Операции, законы = A k = < N k, S k> Соответствия Классификация + Свойства = G A B соответствий Декартова степень An Отношения Rn An Декартов квадрат A 2 Бинарное отношение R 2 A 2 ХНУРЭ, факультет КИУ, кафедра АПВТ, тел. 7021 326, e-mail: ri@kture. kharkov. ua Операции, = Ar = < N r , Sr > + законы R~ A 2 R A 2 17

Упорядоченные множества. Отношение порядка 2011 Тест-вопросы 1. Если отношение антирефлексивно, антисимметрично и транзитивно, оно является: а) отношением нестрогого порядка; б) отношением строгого порядка; в) не является отношением порядка. 2. Если любые два элемента множества M, на котором задано отношение порядка, сравнимы, М является: а) неупорядоченным; ХНУРЭ, факультет КИУ, кафедра АПВТ, б) тел. 7021 326, e-mail: ri@kture. kharkov. ua линейно упорядоченным; 3. Среди следующих отношений, заданных на множестве отрезков, укажите отношение порядка: а) отрезок х равен отрезку у; б) отрезок х короче отрезка у в 2 раза; в) отрезок х длиннее отрезка у. 18