Дискретна математика Розфарбування графів. Хроматичне число. Хроматичний клас. Лекція 5 І. Г. Гусарова Факультет Прикладної математики та менеджменту
Мета лекції – розглянути означення, характеристику, властивості хроматичного числа, хроматичного класу та числа внутрішньої стійкості. Зміст : Хроматичне число; Теорема Кеніга; Хроматичний клас; Теорема Візінга; Число внутрішньої стійкості; Теорема Шеннона.
Література М. Ф. Бондаренко, Н. В. Білоус. Комп’ютерна дискретна математика. – Харків: “Компанія СМІТ”, 2004. – 480 с. А. Д. Тевяшев, І. Г. Гусарова. Основи дискретной математики в прикладах і задачах: Навч. Посібник для студентів напрямку «Прикладн математика» . – Харків: ХТУРЕ, 2001. – 272 с. Таран Т. А. Основы дискретной математики. – К. : Просвіта, 2003. Бардачов Ю. М. , Соколова Н. А. , В. Є. Ходаков. Дискретна математика: Підручник. –К. : Вища шк. , 2002.
Хроматичне число
Хроматичне число Наприклад, граф, показаний на малюнку, є 5 -хроматичним, 4 хроматичним, 3 -хроматичним.
Хроматичне число
Хроматичне число 3. Якщо залишилися вершини, що мають обраніше критичні кольори, то повторюємо крок 2 для цих кольорів. Якщо ні, то вибираємо в якості критичного інші кольори. Повторюємо крок 2 доти, поки це можливо. Приклад. На мал. 1 наведений граф, пофарбований в 4 кольори (їм відповідають цифри 1, 2, 3, 4). рис. 1
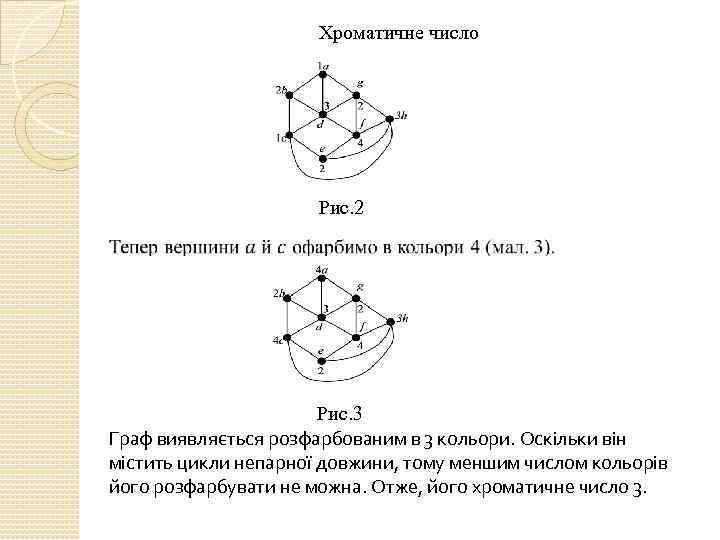
Хроматичне число Рис. 2 Рис. 3 Граф виявляється розфарбованим в 3 кольори. Оскільки він містить цикли непарної довжини, тому меншим числом кольорів його розфарбувати не можна. Отже, його хроматичне число 3.
Хроматичне число Помітимо, що описаний вище спосіб не завжди приводить до відшукання хроматичного числа графа. У книзі Крістофідеса “Теорія графів” наведені й інші способи відшукання хроматичного числа графа, у тому числі й позбавлені зазначеного недоліку - вони завжди приводять до шуканого результату.
Хроматичний клас
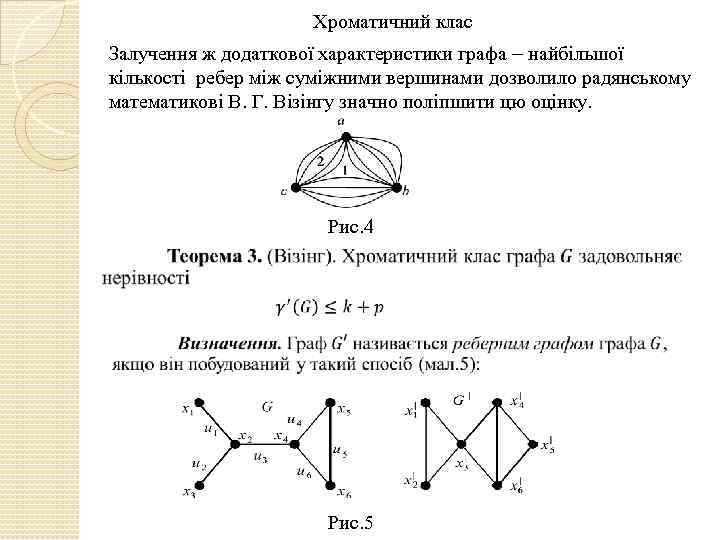
Хроматичний клас Залучення ж додаткової характеристики графа найбільшої кількості ребер між суміжними вершинами дозволило радянському математикові В. Г. Візінгу значно поліпшити цю оцінку. Рис. 4 Рис. 5
Хроматичний клас
Число внутрішньої стійкості
Число внутрішньої стійкості
Число внутрішньої стійкості
Число внутрішньої стійкості
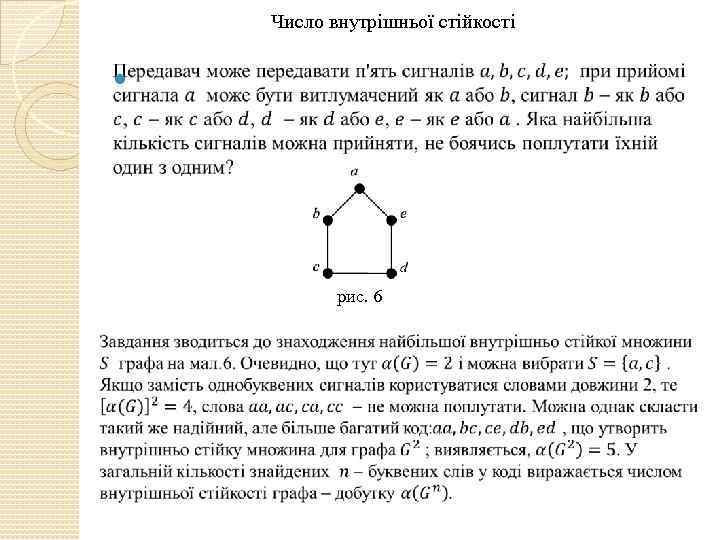
Число внутрішньої стійкості рис. 6
Число внутрішньої стійкості Цей приклад разом з теоремою 5 приводить до наступного визначення.
Скачать презентацию Дискретна математика Розфарбування графів Хроматичне число Хроматичний клас
Розфарбування.pptx