Дискретизация по времени Дискретность времени Время

Дискретизация по времени

Дискретность времени • Время в цифровой системе дискретно. • Для измерения времени вместо секунд и долей секунды используется номер отсчета или количество отсчетов. • Отсутствует информация о сигнале между отсчетами t 1 и t 2. • При дискретно-аналоговом преобразовании сигнала считается, что между отсчетами сигнал неизменен.

• Выбор частоты дискретизации критически важен, поскольку влияет на множество параметров всего проекта. • От частоты дискретизации зависит величина потока данных, проходящих через вычислитель. Соответственно, на основании частоты дискретизации выбирается производительность вычислителя, потребные объемы памяти, вид и скорость шин передачи данных. • От этих деталей, в свою очередь, зависит энергопотребление системы, габариты и количество слоев печатной платы, параметры источника питания. • Все это в конечно счете влияет на размеры устройства и его стоимость.

Прохождение сигналов различных частот через дискретизатор Пусть сигнал на входе описывается гармонической функцией x(t)=Cos[2 pi(m+a)fdt+j)] , m=1, 2, 3. . . , 0 a 1 Частота этого сигнала превышает частоту дискретизации в (m+a) раз. Подставив fd=1/τ и введя дискретное время tk=kτ, мы получим сигнал xk=Cos(2 p(m+a)k+j) = Cos(2 pak+j), который для всех моментов времени tk неотличим от сигнала частоты afd.

Прохождение сигналов различных частот через дискретизатор Если в спектре входного сигнала присутствуют частоты выше fd/2 , то в процессе дискретизации энергия этих составляющих переносится в область частот ниже fd/2 и суммируется с энергией спектральных составляющих, лежащих в этой области. В результате описанного эффекта наложения происходит необратимое искажение (маскировка) ряда спектральных составляющих исходного сигнала, что исключает возможность его точного восстановления по дискретизированному.

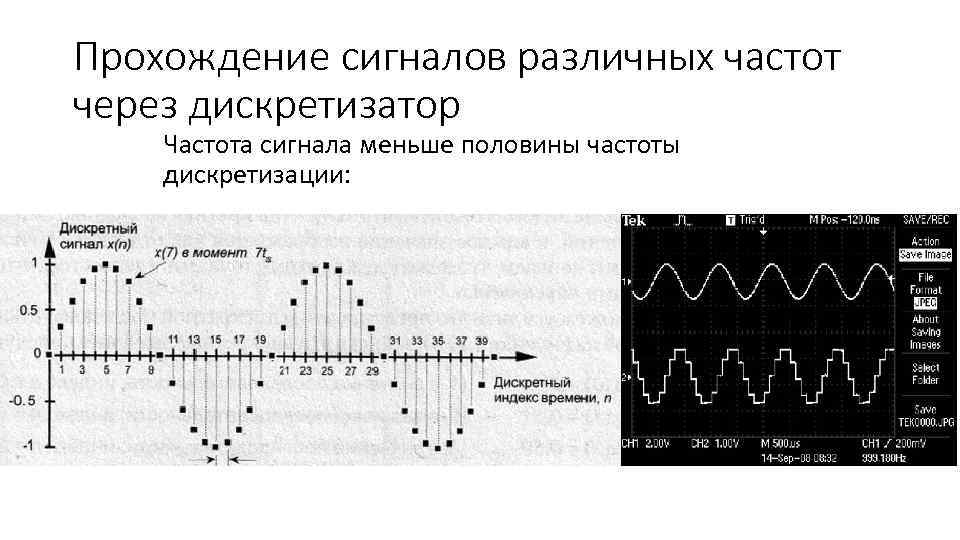Прохождение сигналов различных частот через дискретизатор Частота сигнала меньше половины частоты дискретизации:

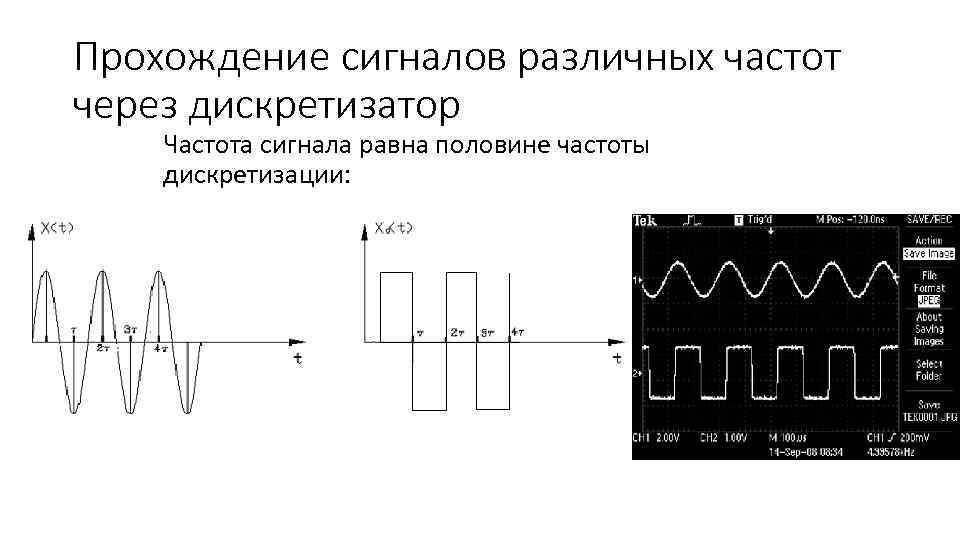Прохождение сигналов различных частот через дискретизатор Частота сигнала равна половине частоты дискретизации:

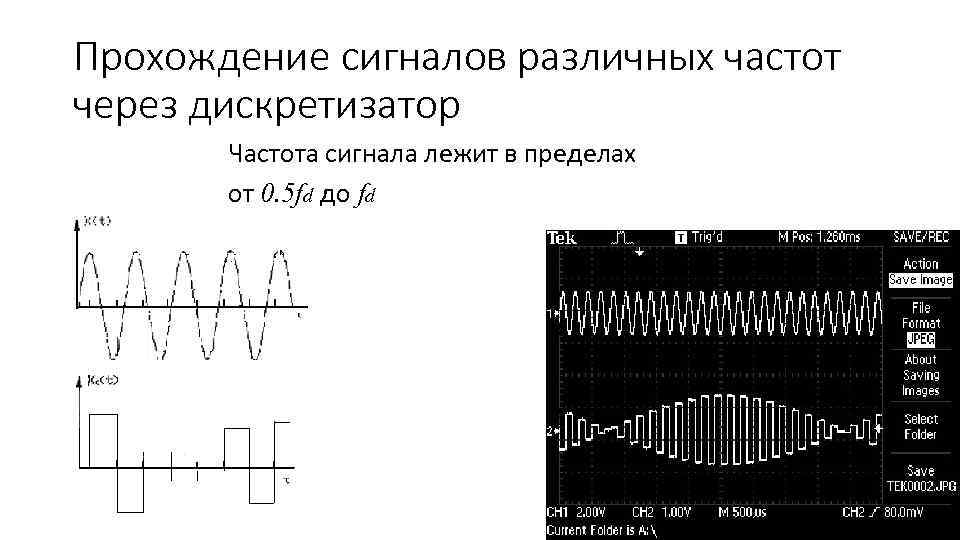Прохождение сигналов различных частот через дискретизатор Частота сигнала лежит в пределах от 0. 5 fd до fd

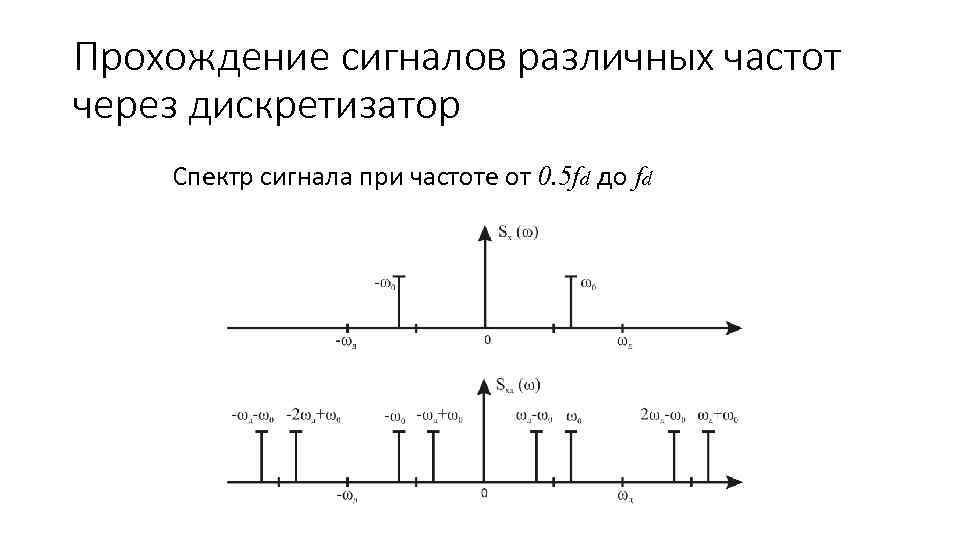Прохождение сигналов различных частот через дискретизатор Спектр сигнала при частоте от 0. 5 fd до fd

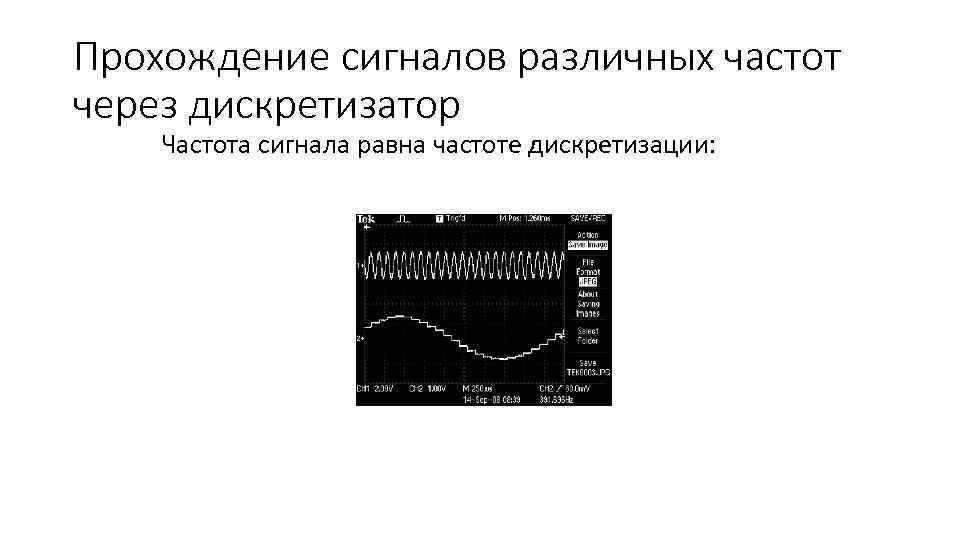Прохождение сигналов различных частот через дискретизатор Частота сигнала равна частоте дискретизации:

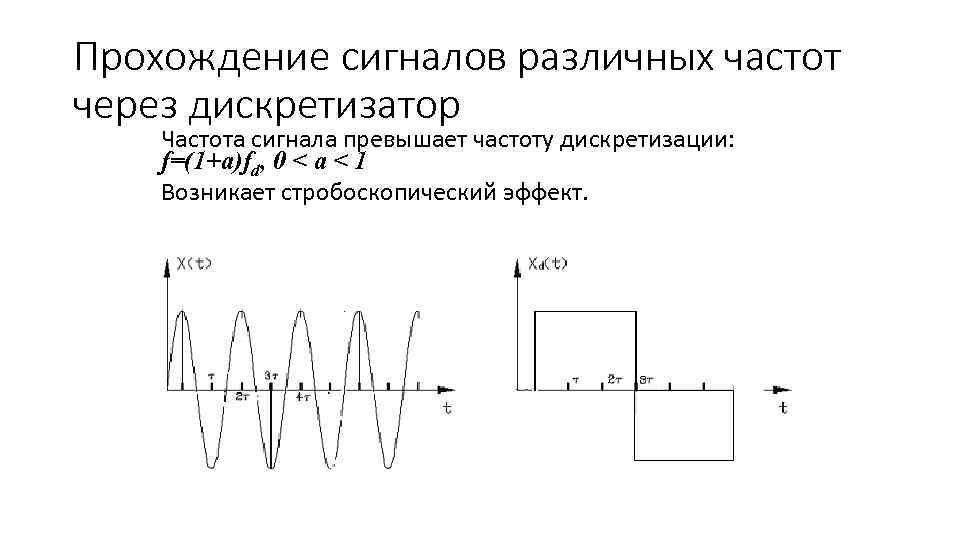Прохождение сигналов различных частот через дискретизатор Частота сигнала превышает частоту дискретизации: f=(1+a)fd, 0 < a < 1 Возникает стробоскопический эффект.