ДИСКОНТИРОВАНИЕ ДЕНЕЖНЫХ ПОТОКОВ БУДУЩАЯ И ТЕКУЩАЯ СТОИМОСТЬ

ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ • Простые проценты • Сложные проценты • Процентная ставка 2

ПРОЦЕНТЫ • Проценты – это доход от предоставления капитала в долг в различных формах (ссуды, кредиты и т. д. ), либо от инвестиций производственного и финансового характера 3

ПРОСТЫЕ ПРОЦЕНТЫ Проценты, начисляемые только на основную сумму, независимо от процентов, накопленных в прошлом. 4

ПРИМЕР • Ссуда в размере 500, 000 у. е. выдана на 3 года по простой ставке процента 30% годовых. Проценты за 3 года составят: • 500, 000 у. е. × 30% × 3 = 450, 000 у. е. 5

СЛОЖНЫЕ ПРОЦЕНТЫ • Проценты начисляются на невыплаченные проценты прошлых периодов и на основную сумму. 6

ПРИМЕР • Если бы сейчас нам предстояло вложить 1, 000 у. е. в банк под 10% годовых с расчетом выплаты процентов раз в год (в конце года), то мы рассчитывали бы на следующие показатели доходности: • (а) через год стоимость инвестиции увеличилась бы до следующей величины: 1, 000 у. е. + 10% от 1, 000 у. е. = 1, 000 у. е. × (1 + 10%) = 1, 000 у. е. × (1. 10) = 1, 100 у. е. • Доходы по % составили бы 100 у. е. 7

ПРИМЕР • (б) если бы мы держали свои деньги на этом банковском счете, то через два года стоимость инвестиции составила бы 1, 210 у. е. (1, 100 у. е. × 1. 1). Доходы по процентам за второй год составили бы 110 у. е. (1, 210 у. е. . – 1, 100 у. е. ) 8

ПРОЦЕНТНАЯ СТАВКА • Проценты обычно выражаются в годовой ставке, но когда период начисления короче одного года, то процентная ставка на этот период должна быть определена. 9

СТОИМОСТЬ ДЕНЕГ • Будущая стоимость– стоимость в будущем, инвестированных сейчас денежных средств • FV=PV* (1+r)n • r-ставка % за период • n-количество периодов 10

ПРИМЕР • Предположим, что мы инвестируем 2, 000 у. е. под 10%. Какова будет стоимость инвестиции через 5 лет? • Решение • Будущая стоимость 1 доллара через n лет при ставке 10% приведена в таблице C-3. FV = 2, 000 у. е. × 1. 611 = 3, 222 у. е. 11

СТОИМОСТЬ ДЕНЕГ • Текущая (дисконтированная или приведенная) стоимость • PV=FV x [1(1+r)n ] 12

ПРИМЕР • Текущая стоимость 1 у. е. за различные периоды и по разным процентным ставкам приведена в таблице C-1. • Возвращаясь к примеру, для того чтобы через четыре года стоимость инвестиции составила 5, 000 у. е. приставке 6%, нам необходимо вложить следующую сумму: PV = 5, 000 у. е. × [1 / (1. 06)4] = 5, 000 у. е. × 0. 792 = 3, 960 у. е. 13

АННУИТЕТ Аннуитет -Ряд равновеликих выплат (рент), производимых через равные промежутки времени • Аннуитет постнумерандо • Аннуитет пренумерандо 14

АННУИТЕТ • Аннуитет постнумерандо – каждая рента выплачивается в конце периода(все таблицы дисконтирования – постнумерандо) 15

АННУИТЕТ • Аннуитет пренумерандо – каждая рента выплачивается в начале периода(*коэффициент(1+r)) 16

АННУИТЕТЫ ОТЛИЧАЮТСЯ: • Величиной платежей • Интервалом времени между выплатами • Сроком от начала до конца выплат • % ставкой 17

БУДУЩАЯ СТОИМОСТЬ АННУИТЕТА FVА • Мы можем инвестировать в течение 3 -х лет $250 по ставке 10% годовых с начислением процентов каждый год 18

FV=PV X (1+R)N • 1 год 250 х (1+0, 1)2=250 х1, 21=302, 50 • 2 год 250 х (1+0, 1)1=250 х1, 10=275, 00 • 3 год 250 х 1 = 250 х1 =250 • 3, 31=827. 50 19

ТЕКУЩАЯ СТОИМОСТЬ АННУИТЕТА PVА • Найти текущую стоимость аннуитета в 250 долларов на три года под 10% годовых, выплачиваемых в конце каждого года 20

PV=FV X N] [1(1+R) • 1 год 250 х 1(1+0, 1)1=250 х 0, 9091=227, 28 • 2 год 250 х 1(1+0, 1)2=250 х 0, 8264=206, 61 • 3 год 250 х 1(1+0, 1)3=250 х 0, 7513=187, 83 • 2, 4869=621, 72 21

ПРАКТИЧЕСКАЯ РАБОТА ПО ДИСКОНТИРОВАНИЮ • 1. Рассчитайте, какая сумма накопится при инвестиции в размере 10, 000 у. е. под 10% по истечении пяти лет? 22

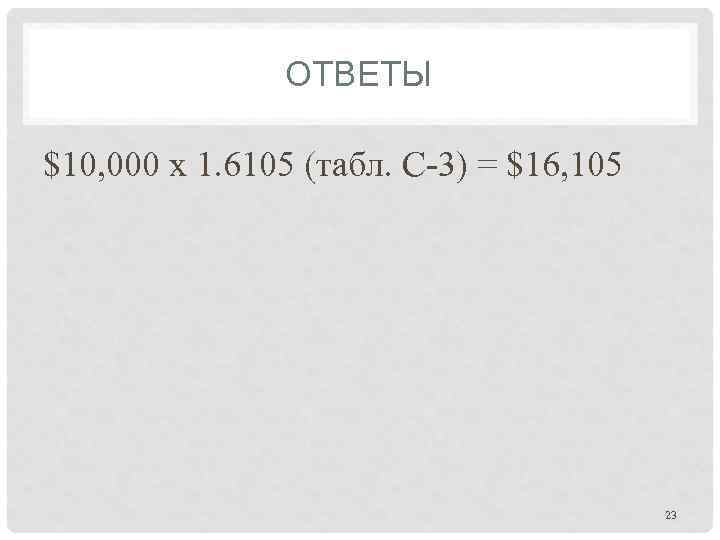
ОТВЕТЫ $10, 000 x 1. 6105 (табл. C-3) = $16, 105 23

ПРАКТИЧЕСКАЯ РАБОТА ПО ДИСКОНТИРОВАНИЮ • 2. Определите текущую стоимость 80, 000 у. е. , которая должна быть получена через 10 лет при процентной ставке 12%. 24

ОТВЕТЫ $80, 000 x 0. 3220 (табл. C-1) = $25, 760 25

ПРАКТИЧЕСКАЯ РАБОТА ПО ДИСКОНТИРОВАНИЮ • 3. Согласно арендному контракту должна производиться ежегодная арендная плата в размере 6, 000 у. е. на протяжении семи лет. Предусмотренная процентная ставка составляет 15%. Какова текущая стоимость арендных платежей? 26

ОТВЕТЫ $6, 000 x 4. 1604 (табл. C-2) = $24, 962 27

ПРАКТИЧЕСКАЯ РАБОТА ПО ДИСКОНТИРОВАНИЮ • 4. Инвестор намерен вкладывать в конце каждого года по 15, 000 у. е. в течение последующих 9 лет под 14% годовых. Какая сумма будет в фонде по истечении 9 лет? 28

ОТВЕТЫ 15, 000 x 16. 0853 (табл. C-4) = $241, 280 29

ПРАКТИЧЕСКАЯ РАБОТА ПО ДИСКОНТИРОВАНИЮ • 5. Если можно вложить 731, 190 сейчас, какой должна быть процентная ставка, чтобы через 3 года накопилось 1. 000, 000? 30

ОТВЕТЫ Таблица С-3 1, 000 / 731, 190 =1. 36763 3 года- 11% 31

ПРАКТИЧЕСКАЯ РАБОТА ПО ДИСКОНТИРОВАНИЮ Какую сумму необходимо вложить под 10% годовых 1 января 1995 года, чтобы каждый год, начиная с 1 января 1996 года, получат выплаты по 5, 000 у. е. ? Последняя выплата произойдет 1 января 1999 года. • 6. 32

ОТВЕТЫ • • • Таблица С-2 PVOA(10%, 4 п) =3, 1699 5, 000 * 3, 1699 = 15850 33

ПРАКТИЧЕСКАЯ РАБОТА ПО ДИСКОНТИРОВАНИЮ 7. Какую сумму нужно вкладывать в конце каждого года на счет под 9% годовых, если необходимо к концу пятого года накопить 10, 000 у. е. ? 34

ОТВЕТЫ Таблица С-4 10, 000 = А* FVOA(9%. 5 п) А = 10, 000 / 5, 9847 = 1, 671 35

ПРАКТИЧЕСКАЯ РАБОТА ПО ДИСКОНТИРОВАНИЮ • 8. Вы выиграли в лотерею 10 миллионов. По условиям лотереи существует 2 способа получения выигрыша: • 1) получать по 1, 000 у. е. ежегодно на протяжении 10 лет; • 2) получить сразу всю сумму выигрыша, которая в этом случае составит 5, 650, 000 у. е. . • Установленная процентная ставка по аналогичным вложениям составляет 10%. Какой способ получения выигрыша вы выберете 36

ОТВЕТЫ $1, 000 x 6. 1446 (табл. C-2) = $6, 144, 600 37