Discriminant analysis Chapter 11 Statistics for Marketing

Discriminant analysis Chapter 11 Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi 1

2 -groups discriminant analysis • Discriminant analysis is a statistical procedure which allows us to classify cases in separate categories to which they belong on the basis of a set of characteristic independent variables called predictors or discriminant variables • The target variable (the one determining allocation into groups) is a qualitative (nominal or ordinal) one, while the characteristics are measured by quantitative variables. • DA looks at the discrimination between two groups • Multiple discriminant analysis (MDA) allows for classification into three or more groups. Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi 2

Applications of DA • DA is especially useful to understand the differences and factors leading consumers to make different choices allowing them to develop marketing strategies which take into proper account the role of the predictors. • Examples • Determinants of customer loyalty • Shopper profiling and segmentation • Determinants of purchase and non-purchase Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi 3

Example on the Trust data-set • Purchasers of chicken at the butcher’s shop (recorded in question q 8 d) • Respondents may belong to one of two groups • those who purchase chicken at the butcher’s shop • those who do not • Discrimination between these groups through a set of consumer characteristics • expenditure on chicken in a standard week (q 5) • age of the respondent (q 51) • whether respondents agree (on a seven-point ranking scale) that butchers sell safe chicken (q 21 d) • trust (on a seven-point ranking scale) towards supermarkets (q 43 b) • Does a linear combination of these four characteristics allow one to discriminate between those who buy chicken at the butcher’s and those who do not? Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi 4

Discriminant analysis(DA) • Two groups only, thus a single discriminating value (discriminating score) • For each respondent a score is computed using the estimated linear combination of the predictors (the discriminant function) • Respondents with a score above the discriminating value are expected to belong to one group, those below to the other group. • When the discriminant score is standardized to have zero mean and unity variance it is called Z score • DA also provides information about the discriminating power of each of the original predictors Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi 5

Multiple discriminant analysis(MDA)(1) • Discriminant analysis may involve more than two groups, in which case it is termed multiple discriminant analysis (MDA). • Example from the Trust data-set • Dependent variable: Type of chicken purchased ‘in a typical week’, choosing among four categories: value (good value for money), standard, organic and luxury • Predictors: age (q 50), stated relevance of taste (q 24 a), value for money (q 24 b) and animal welfare (q 24 k), plus an indicator of income (q 60) Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi 6

Multiple discriminant analysis(2) • In this case there will be more than one discriminant function. • The exact number of discriminant functions is equal to either (g-1), where g is the number of categories in classification or to k, the number of independent variables, whichever is the smaller • Trust example: four groups and five explanatory variables, the number of discriminant functions is three (that is g-1 which is smaller than k=5). Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi 7

The output of MDS • Similarities with factor (principal component) analysis • the first discriminant function is the most relevant for discriminating across groups, the second is the second most relevant, etc. • the discriminant functions are also independent, which means that the resulting scores are non-correlated. • Once the coefficients of the discriminant functions are estimated and standardized, they are interpreted in a similar fashion to the factor loadings. • The larger the standardised coefficients (in absolute terms), the more relevant the respective variables to discriminating between groups • There is no single discriminant score in MDA • group means are computed (centroids) for each of the discriminant functions to have a clearer view of the classification rule Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi 8

Running discriminant analysis (two groups) Discriminant function (Target variable: purchasers of chicken at the butcher’s shop) Discriminant score Predictors • weekly expenditure on chicken The a discriminant coefficients need to be estimated • age • safety of butcher’s chicken • trust in supermarkets Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi 9

Fisher’s linear discriminant analysis • • The discrimant function is the starting point Two key assumptions behind linear DA (a) the predictors are normally distributed; (b) the covariance matrices for the predictors within each of the groups are equal. • • • Departure from condition (a) should suggest use of alternative methods (logistic regression, see lecture 16) Departure from condition (b) requires the use of different discriminant techniques (usually quadratic discriminant functions). In most empirical cases, the use of linear DA is appropriate Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi 10

Estimation • The first step is the estimation of the a coefficients, also termed as discriminant coefficients or weights • Estimation is similar to factor analysis or PCA, as the coefficients are those which maximize the variability between groups • In MDA the first discriminating function is the one with the highest between-group variability, the second discriminating function is independent from the first and maximizes the remaining betweengroup variability and so on Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi 11

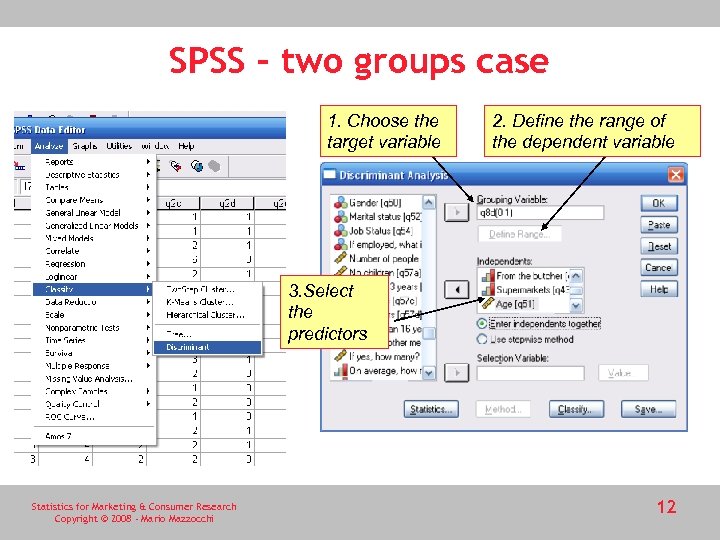SPSS – two groups case 1. Choose the target variable 2. Define the range of the dependent variable 3. Select the predictors Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi 12

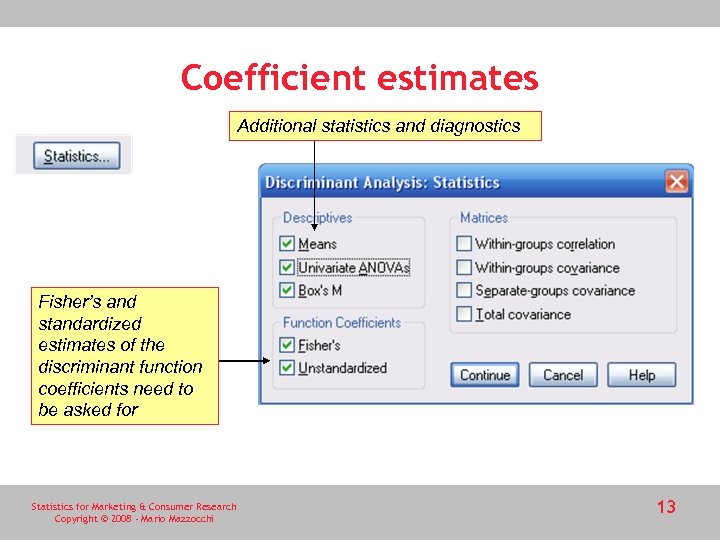Coefficient estimates Additional statistics and diagnostics Fisher’s and standardized estimates of the discriminant function coefficients need to be asked for Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi 13

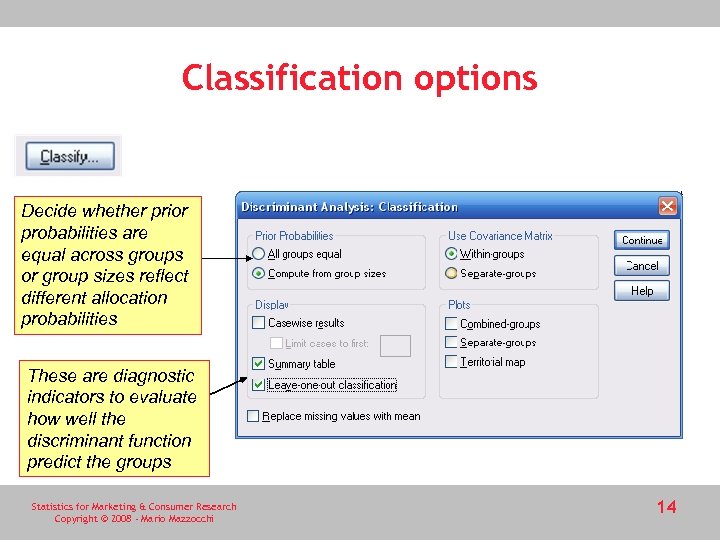Classification options Decide whether prior probabilities are equal across groups or group sizes reflect different allocation probabilities These are diagnostic indicators to evaluate how well the discriminant function predict the groups Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi 14

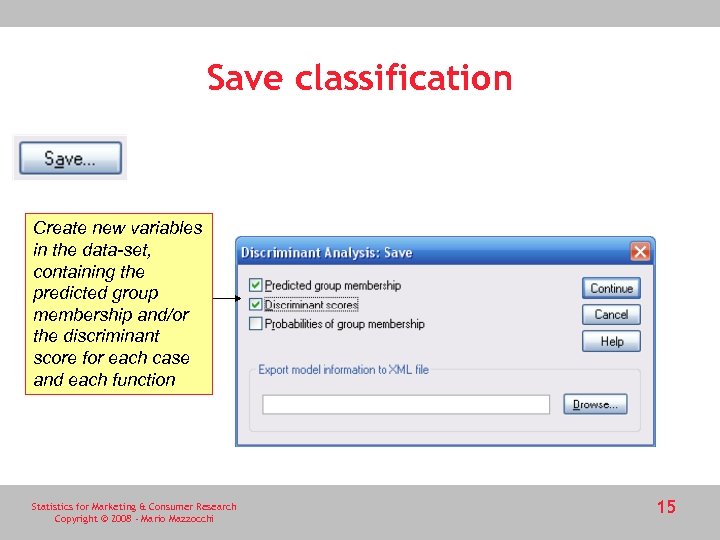Save classification Create new variables in the data-set, containing the predicted group membership and/or the discriminant score for each case and each function Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi 15

Output – coefficient estimates Most important predictor Unstandardized coefficients depend on the measurement unit Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi Standardized coefficients do not depend on the measurement unit Trust in supermarkets has a – sign (thus it reduces the discriminant score) 16

Centroids These are the means of the discriminant score for each of the two groups Thus, the group of those not purchasing chicken at the butcher’s shop have a negative centroid With two groups, the discriminating score is zero This can be computed by weighting the centroids with the initial probabilities From these prior probabilities it follows that the discriminating score is -0. 307 x 0. 66 + 0. 594 x 0. 34 = 0 Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi 17

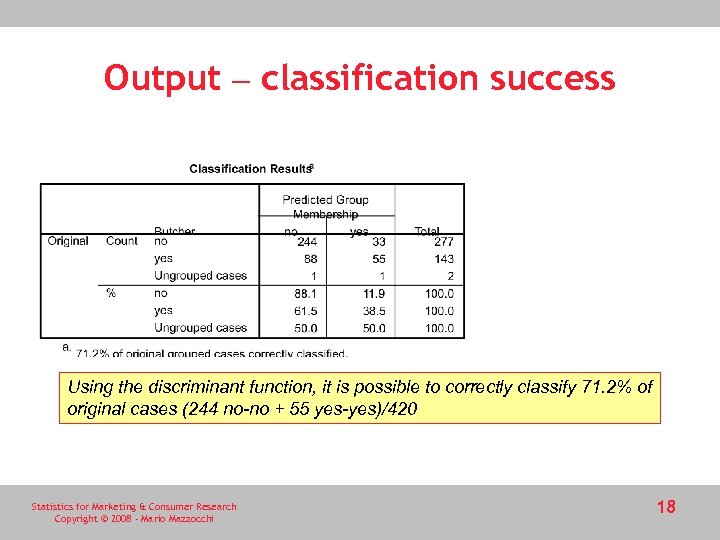Output – classification success Using the discriminant function, it is possible to correctly classify 71. 2% of original cases (244 no-no + 55 yes-yes)/420 Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi 18

Diagnostics (1) • Box’s M test. This tests whether covariances are equal across groups • Wilks’ Lambda (or U statistic) tests discrimination between groups. It is related to analysis of variance. • Individual Wilks’Lambda for each of the predictors in a discriminant function; univariate ANOVA (are there significant differences in the predictor’s means between the groups? ), p-value from the F distribution. • Wilks’ Lambda for the function as a whole. Are there significant differences in the group means for the discriminant function p-value from the Chi-square distribution? • The overall Wilks’ Lambda is especially helpful in multiple discriminant analysis as it allows one to discard those functions which do not contribute towards explaining differences between groups. Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi 19

Diagnostics (2) • DA returns one eigenvalue (or more eigenvalues for MDA) of the discriminant function. • These can be interpreted as in principal component analysis • In MDA (more than one discriminant function) eigenvalues are exploited to compute how each function contributes to explain variability • The canonical correlation measures the intensity of the relationship between the groups and the single discriminant function Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi 20

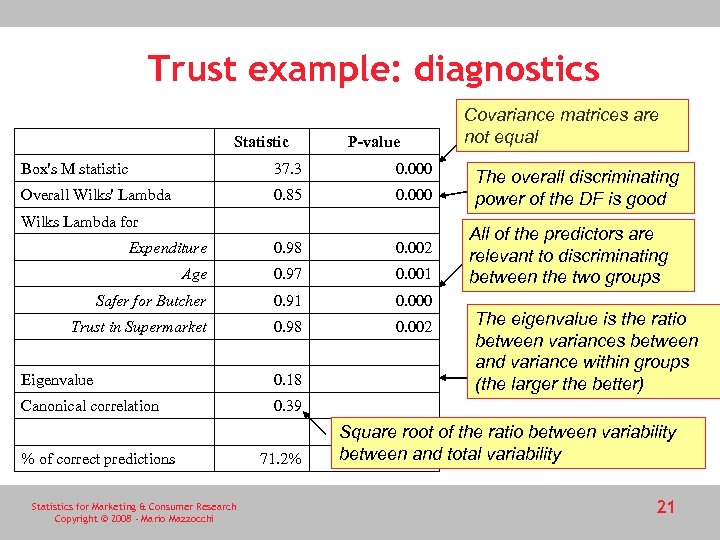Trust example: diagnostics Statistic P-value Box's M statistic 37. 3 0. 000 Overall Wilks' Lambda 0. 85 0. 000 Expenditure 0. 98 0. 002 Age 0. 97 0. 001 Safer for Butcher 0. 91 0. 000 Trust in Supermarket 0. 98 0. 002 Wilks Lambda for Eigenvalue 0. 18 Canonical correlation Covariance matrices are not equal The overall discriminating power of the DF is good All of the predictors are relevant to discriminating between the two groups The eigenvalue is the ratio between variances between and variance within groups (the larger the better) 0. 39 % of correct predictions Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi 71. 2% Square root of the ratio between variability between and total variability 21

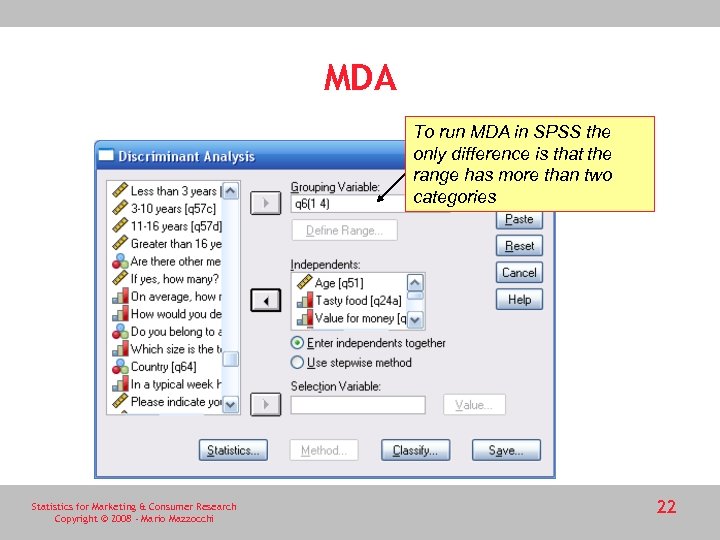MDA To run MDA in SPSS the only difference is that the range has more than two categories Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi 22

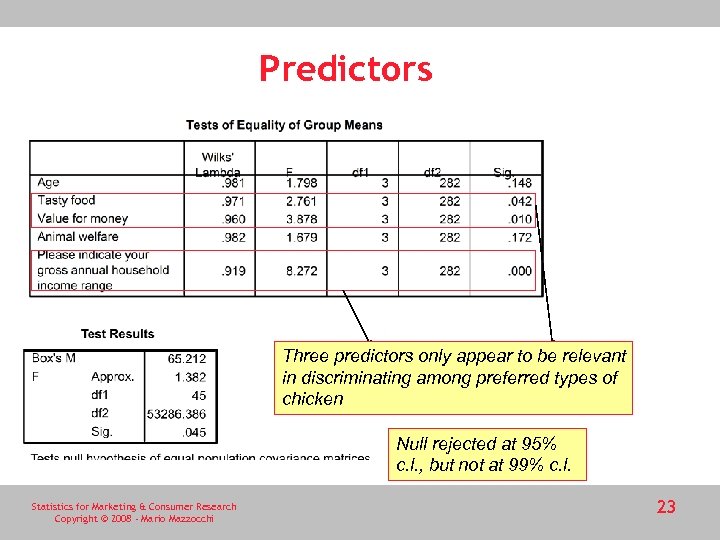Predictors Three predictors only appear to be relevant in discriminating among preferred types of chicken Null rejected at 95% c. l. , but not at 99% c. l. Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi 23

Discriminant functions Three discriminant functions (four groups minus one) can be estimated The first two discriminant functions have a significant discriminating power. Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi 24

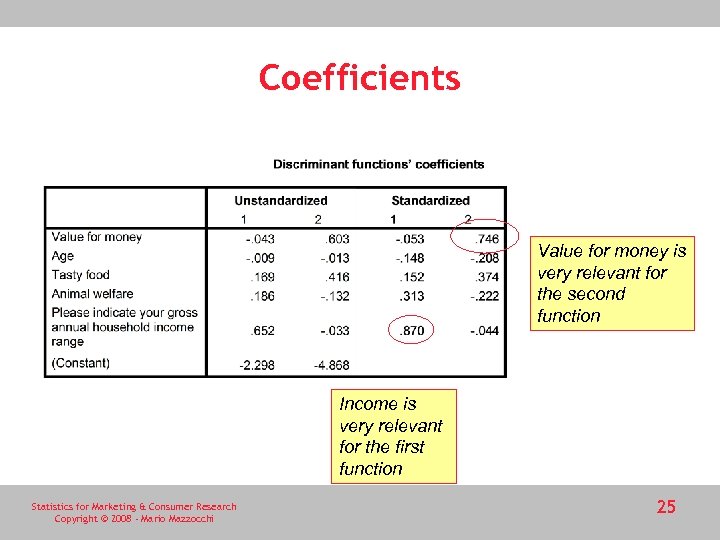Coefficients Value for money is very relevant for the second function Income is very relevant for the first function Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi 25

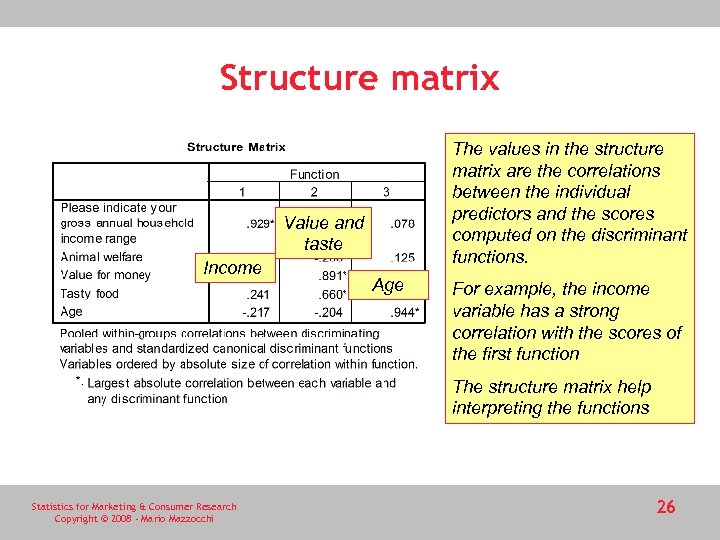Structure matrix The values in the structure matrix are the correlations between the individual predictors and the scores computed on the discriminant functions. Value and taste Income Age For example, the income variable has a strong correlation with the scores of the first function The structure matrix help interpreting the functions Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi 26

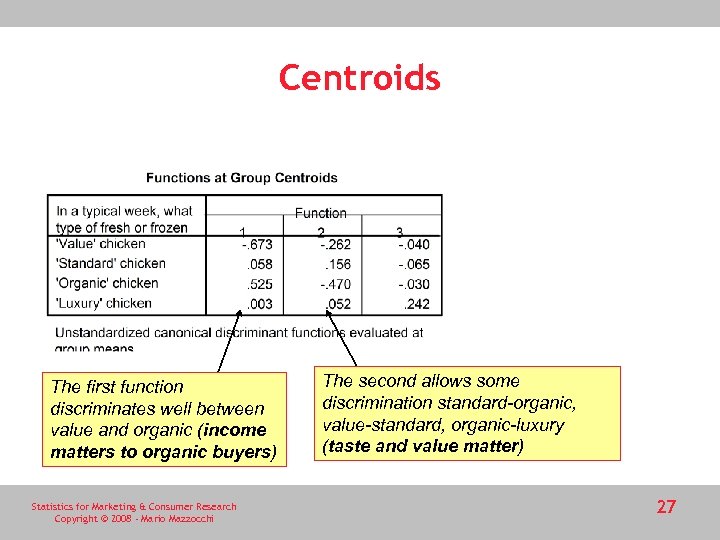Centroids The first function discriminates well between value and organic (income matters to organic buyers) Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi The second allows some discrimination standard-organic, value-standard, organic-luxury (taste and value matter) 27

Plot of two functions Tick ‘separate-groups’ to show graphs of the first two functions for each individual group The ‘territorial map’ shows the scores for the first two functions considering all groups Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi 28

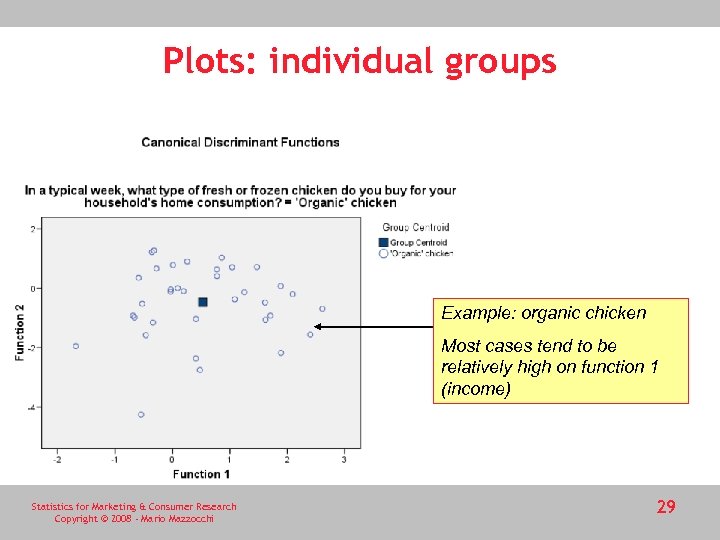Plots: individual groups Example: organic chicken Most cases tend to be relatively high on function 1 (income) Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi 29

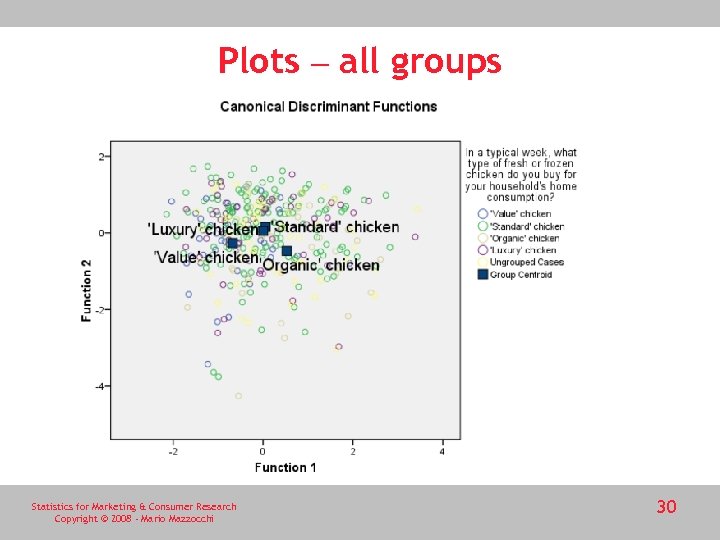Plots – all groups Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi 30

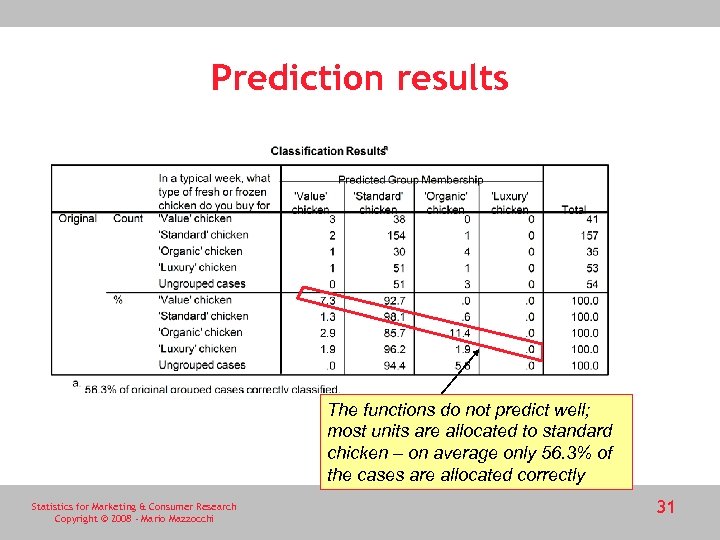Prediction results The functions do not predict well; most units are allocated to standard chicken – on average only 56. 3% of the cases are allocated correctly Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi 31

Stepwise discriminant analysis • As for linear regression it is possible to decide whether all predictors should appear in the equation regardless of their role in discriminating (the Enter option) or a subset of predictors is chosen on the basis of their contribution to discriminating between groups (the Stepwise method) Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi 32

The step-wise method 1. 2. 3. 4. 5. A one-way ANOVA test is run on each of the predictors, where the target grouping variable determines the treatment levels. The ANOVA test provides a criterion value and tests statistics (usually the Wilks Lambda). According to the criterion value, it is possible to identify the predictor which is most relevant in discriminating between the groups The predictor with the lowest Wilks Lambda (or which meets an alternative optimality criterion) enters the discriminating function, provided the p-value is below the set threshold (for example 5%). An ANCOVA test is run on the remaining predictors, where the covariates are the target grouping variables and the predictors that have already entered the model. The Wilks Lambda is computed for each of the ANCOVA options. Again, the criteria and the p-value determine which variable (if any) enter the discriminating function (and possibly whether some of the entered variables should leave the model). The procedure goes back to step 3 and continues until none of the excluded variables have a p-value below the threshold and none of the entered variables have a p-value above threshold (the stopping rule is met). Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi 33

Alternative criteria • • Unexplained variance Smallest F ratio Mahalanobis distance Rao’s V Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi 34

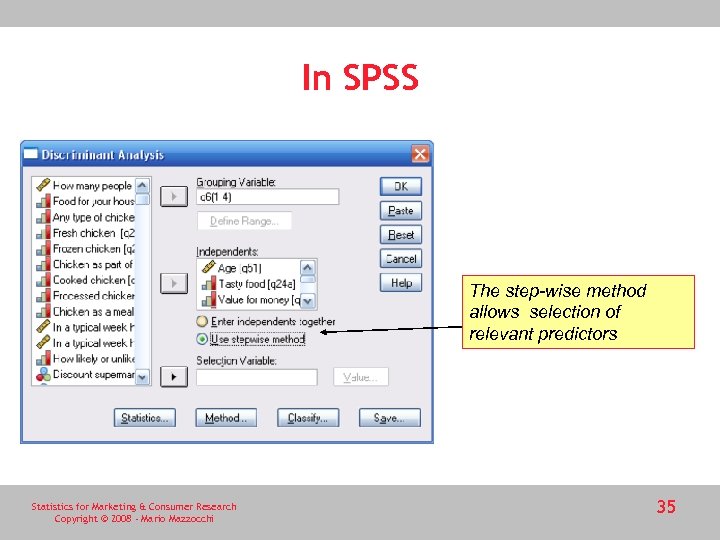In SPSS The step-wise method allows selection of relevant predictors Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi 35

Output of the step-wise method Only two predictors are kept in the model Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi 36