63bd4cec1faa0d3d3fd6be5d91830804.ppt
- Количество слайдов: 27

Discrete Random Variables: The Binomial Distribution

Bernoulli’s trials J. Bernoulli (1654 -1705) analyzed the idea of repeated independent trials for discrete random variables that had two possible outcomes: success or failure n In his notation he wrote that the probability of success is denoted by p and the probability of failure is denoted by q or 1 -p n

Binomial distribution The binomial distribution is just n independent individual (Bernoulli) trials added up. n It is the number of “successes” in n trials. n The sum of the probabilities of all the independent trials totals 1. n We can define a ‘success’ as a ‘ 1’, and a failure as a ‘ 0’. n

Binomial distribution n “x” is a binomial distribution if its probability function is: probability of success probability of failure n Examples (note – success/failure could be switched!): Situation x=1 (success) x=0 (failure) Coin toss to get heads Turns up tails Rolling dice to get 1 Lands on anything but 1 While testing a product, how many are found defective Product is not defective

Binomial distribution The binomial distribution is just n independent ‘Bernoulli trials’ added up n. It requires that the trials be done “with replacement” ex. testing bulbs for defects: n • Let’s say you make many light bulbs • Pick one at random, test for defect, put it back • Repeat several times • If there are many light bulbs, you do not have to replace (it won’t make a significant difference) • The result will be the binomial probability of a defective bulb (#defective total sample).

Binomial distribution - formula Let’s figure out a binomial random variable’s probability function or formula n Suppose we are looking at a binomial with n=3 (ex. 3 coin flips; ‘heads’ is a ‘success’) n We will start with ‘all tails’ P(x=0): n ¨ Can happen only one way: 000 ¨ Which is: (1 -p)(1 -p) ¨ Simplified: (1 -p)3

Binomial distribution - formula Let’s figure out a binomial probability function (for n = 3) n This time we want 1 success plus 2 failures (ex. 1 heads + 2 tails, or P(x=1)): n This can happen three ways: 100, 010, 001 ¨ Which is: p(1 -p)+(1 -p)p(1 -p)+(1 -p)p ¨ Simplified: 3 p(1 -p)2 ¨

Binomial distribution - formula Let’s figure out a binomial probability function (for n = 3) n We want 2 ‘successes’ P(x=2): n Can happen three ways: 110, 011, 101, or… ¨ pp(1 -p)+(1 -p)pp+p(1 -p)p, which simplifies to. . ¨ 3 p 2(1 -p) ¨

Binomial distribution - formula Let’s figure out a binomial probability function (n = 3) n We want all 3 ‘successes’ P(x=3): n This can happen only one way: 111 ¨ Which we represent as: ppp ¨ Which simplifies to: p 3 ¨

Binomial distribution - formula n Let’s figure out a binomial probability function – in summary, for n = 3, we have: P(x) The sum of these expressions is the binomial distribution for n=3. The resulting equation is an example of the Binomial Theorem. (Where x is the number of successes; ex. # of heads)

Binomial distribution - formula n A quick review of the Binomial Theorem: ¨ If we use q for (1 – p), then… ¨ p 3 + 3 p 2 q +3 pq 2 + q 3 = (p + q)3 ¨ which is an example of the formula: (a + b)n = __________ (if you forget it, check it in your text)

Binomial distribution - formula n Let’s figure out a binomial r. v. ’s probability function (the quick way to compute the sum of the terms on the previous slide) now here’s the formula… ¨In general, for a binomial: (the # of x successes with probability p in n trials)

Binomial distribution - formula ¨ Which or can be written as: P(x) = n. Cx px(1 – p)n-x This formula is often called the general term of the binomial distribution. ¨

Expected Value n The expected value of a binomial distribution equals the probability of success (p) for n trials: E(X) also equals the sum of the probabilities in the binomial distribution. n
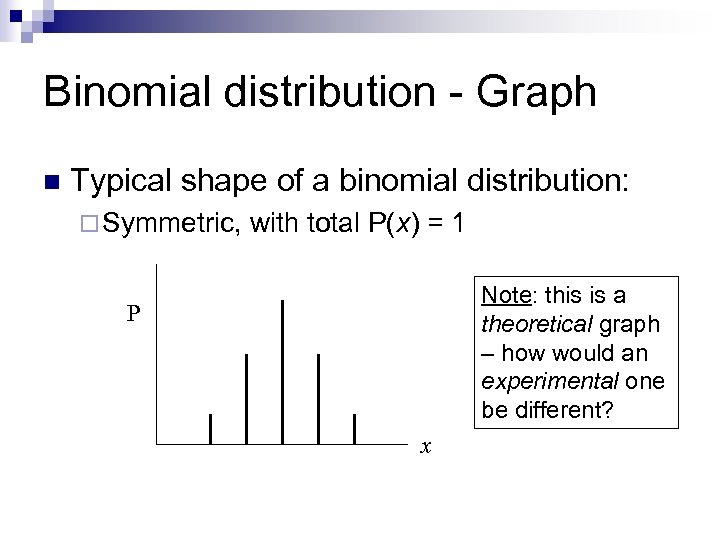
Binomial distribution - Graph n Typical shape of a binomial distribution: ¨ Symmetric, with total P(x) = 1 Note: this is a theoretical graph – how would an experimental one be different? P x

Binomial distribution - example A realtor claims that he ‘closes the deal’ on a house sale 40% of the time. n This month, he closed 1 out of 10 deals. n How likely is his claim of 40% if he only completed 1/10 of his deals this month? n

Binomial distribution - example n By using the binomial distribution function, it’s possible to check if his assessment of his abilities (i. e. 40% ‘closes’) is likely: P(0 deals)=

Binomial distribution - example n So it seems pretty unlikely that his assessment of his abilities is right: ¨The probability of closing 1 or fewer deals out of 10 if (as he claims) he closes deals 40% of the time is less than 5% or less than 1/20. ¨ What % of ‘closes’ do you think would have the highest probability in this distribution, if his claim was right?

Binomial distribution - example n Now see if you can determine the expected number of closings if he had 12 deals this month, assuming 40% success. We need the values of n (= ___) and of p (= ____). n E(X) = np = ______ - this means that we would expect him to close about _____ deals, if his claim is correct. [End of first example. ] n

Binomial Distribution – ex. 2 Alex Rios has a batting average of 0. 310 for the season. In last night’s game, he had 4 at bats. What are the chances he had 2 hits? n You try this one! First ask 3 questions… n

Binomial Distribution – ex. 2 Is ‘getting a hit’ a discrete random variable? n Is this a Bernoulli trial? How would you define a “success” and a “failure”? n n Is each time at bat an independent event? If you can answer ‘yes’ to the three questions above, then you can use the binomial distribution formula to answer the problem. n

Binomial Distribution – ex. 2 n First determine the following values: ¨ The number of trials (Alex is at bat __ times) – this is the value of n ¨ The probability of success (Alex’s average is ___) – this is p ¨ The probability of ‘failure’: 1 – p = ___ ¨ The # of successes asked for (his chances of getting ___ hits) – this is x n Now you can use the formula:

Binomial Distribution – ex. 2 n Put in the values from the previous screen, and discuss your answers. [pause here] n Did you get P(2) = 0. 275? n Is 2 the most likely number of hits for Alex last night? How about 1 or 3? n n P(0 or 1 or 2 or 3 or 4 hits) = _____?

Hypergeometric distribution What happens if you have a situation in which the trials are not independent (this most often happens due to not replacing a selected item). n Each trial must result in success or failure, but the probability of success changes with each trial. n

Hypergeometric distribution Consider taking a sample from a population, and testing each member of the sample for defects. n Do this sampling without replacement. n As long as the sample is small compared to the population, this is close to binomial. n But if the sample is large compared to the population, this is a hypergeometric dist. n

Hypergeometric dist. - formula A hypergeometric distribution differs from binomial ones since it has dependent trials. n Probability of x successes in r dependent trials, with number of successes a out of a total of n possible outcomes: n

Hypergeometric dist. - formula n The full version of this formula is: n Expected Value – the average probability of a success is the ratio of success overall (a/n) times r trials:
63bd4cec1faa0d3d3fd6be5d91830804.ppt