Discrete Random Variables 2 • To understand calculate with cumulative distribution functions • To be able to calculate the mean or expected value of a discrete random variable • To be able to calculate the variance of a discrete random variable
Cumulative Distribution Function The probability that X is less than or equal to x is written as F(x) = P(X ≤ x) 2 coins are thrown. X is the number of heads Sample space HH, HT, TH, TT Cumulative distribution function x P(X=x) F(x) 0 ¼ ¼ 1 ½ ¾ 2 ¼ 1
Problem 1 F(x) = (x + k) 8 x = 1, 2, 3 a) Find k b) Write down the distribution table for the cumulative distribution function c) Write down F(2. 6) d) Find the probability distribution of X
Problem 1 - Solution F(x) = (x + k) 8 x = 1, 2, 3 a) Find k F(3) = 1 so 3 + k = 1 therefore 3+k = 8 and k=5 8 b) F(2) = 2 + 5 = 7 8 8 F(1) = 1 + 5 = 6 8 8 x 1 F(x) 6/ 2 8 7/ 3 8 1
Problem 1 - Solution F(x) = (x + k) 8 x = 1, 2, 3 c) F(2. 6) means P(X≤ 2. 6) = F(2) = 7/8 d) x F(x) 1 2 3 6/ 1/ 1/ 8 8 8
Mean or Expected value of a DRV NB p(x) is the same as P(X=x) Expected value of X = E(X) = Σx. P(X=x) = Σxp(x) Statistics experiment 1. Collect data 2. Frequency distribution 3. Mean value Σfx Σx Theoretical approach 1. Probability distribution 2. Expected value Σxp(x)
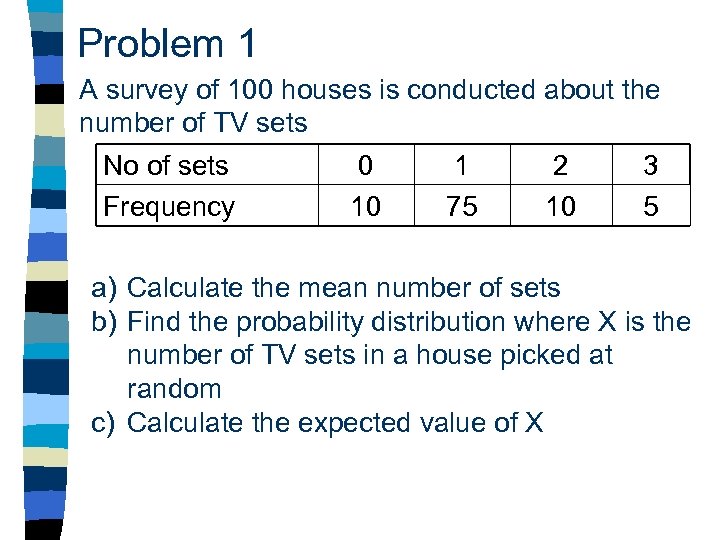
Problem 1 A survey of 100 houses is conducted about the number of TV sets No of sets Frequency 0 10 1 75 2 10 3 5 a) Calculate the mean number of sets b) Find the probability distribution where X is the number of TV sets in a house picked at random c) Calculate the expected value of X
Problem 1 - Solution A survey of 100 houses is conducted about the number of TV sets No of sets 0 1 2 3 Frequency 10 75 10 5 a) Calculate the mean number of sets Mean value Σfx = 0 + 75 + 20 + 15 = 110 = 1. 1 Σx 100 b) x 0 1 2 3 p(x) 0. 1 0. 75 0. 10 0. 05 c) Expected value of X = Σxp(x) = 0 + 0. 75 + 0. 20 + 0. 15 = 1. 1 Note that the mean value = E(X) = 1. 1 E(X) is sometimes called the mean of X
Problem 2 x p(x) 1 0. 1 2 p 3 0. 3 4 q 5 0. 2 Given that E(X)=3 write 2 equations involving p and q and solve the find the value of p and q.
Problem 2 - Solution x p(x) 1 0. 1 2 p 3 0. 3 4 q 5 0. 2 Given that E(X)=3 write 2 equations involving p and q and solve the find the value of p and q. 0. 1 + p + 0. 3 + q + 0. 2 = 1 p + q + 0. 6 = 1 p + q = 0. 4 0. 1 + 2 p + 0. 9 + 4 q + 1 = 3 2 p + 4 q + 2 = 3 2 p + 4 q = 1
Problem 2 - Solution x p(x) 1 0. 1 2 p 3 0. 3 4 q 5 0. 2 Given that E(X)=3 write 2 equations involving p and q and solve the find the value of p and q. p + q = 0. 4 and so p = 0. 4 - q Substitute into 2 p + 4 q = 1 2(0. 4 – q) + 4 q = 1 0. 8 – 2 q + 4 q = 1 0. 8 + 2 q = 1 2 q = 0. 2 and q = 0. 1 p = 0. 3
Problem 3 – Expected value of X² E(X²) = Σx²p(x) E(Xn) = Σxnp(x) A discrete random variable X has a probability distribution x 1 P(X=x) 12/25 2 6/ 25 3 4/ 25 4 3/ 25 Write down the probability distribution for X² b) Find E(X²) a)
Problem 3 – Solution a) a) x 1 x² 1 P(X=x) 12/25 2 4 6/ 25 E(X²) = Σx²p(X=x²) = 12/25 + 24/25 + 36/25 + 48/25 = 120/25 = 4. 8 3 9 4/ 25 4 16 3/ 25
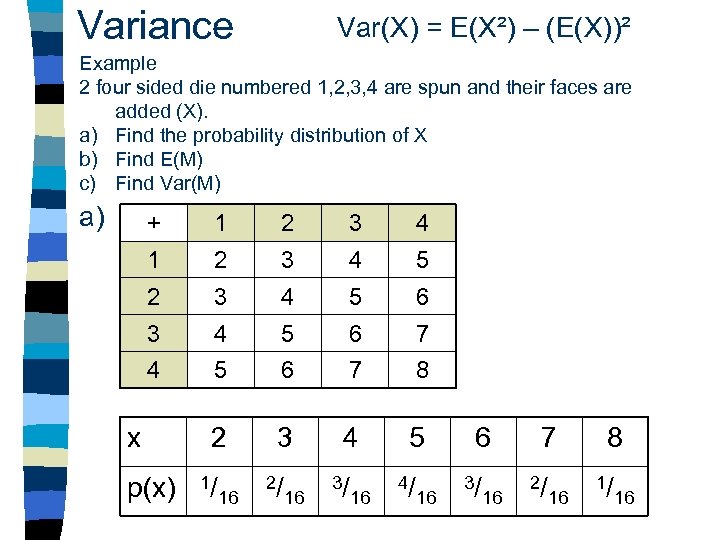
Variance Var(X) = E(X²) – (E(X))² Example 2 four sided die numbered 1, 2, 3, 4 are spun and their faces are added (X). a) Find the probability distribution of X b) Find E(M) c) Find Var(M) a) + 1 2 3 4 5 6 7 4 5 6 7 8 2 3 4 5 x p(x) 1/ 16 2/ 16 3/ 16 4/ 16 6 3/ 16 7 2/ 16 8 1/ 16
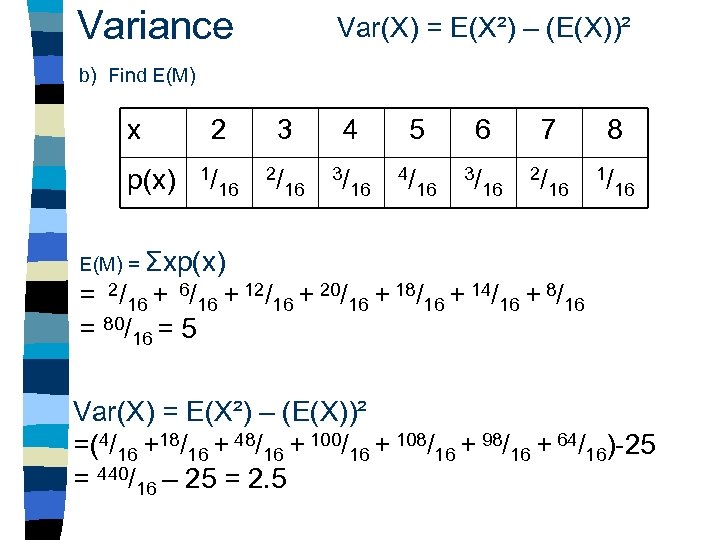
Variance Var(X) = E(X²) – (E(X))² b) Find E(M) x p(x) 2 1/ 16 3 2/ 16 4 3/ 16 5 4/ 16 6 3/ 16 7 2/ 16 8 1/ 16 E(M) = Σxp(x) = 2/16 + 6/16 + 12/16 + 20/16 + 18/16 + 14/16 + 8/16 = 80/16 = 5 Var(X) = E(X²) – (E(X))² =(4/16 +18/16 + 48/16 + 100/16 + 108/16 + 98/16 + 64/16)-25 = 440/16 – 25 = 2. 5
Скачать презентацию Discrete Random Variables 2 To understand calculate
4e44fa8985cae993d250e27774e16b44.ppt