87fba237d25c889153b6eb817e4b8ef5.ppt
- Количество слайдов: 39

Discrete Math CS 2800 Prof. Bart Selman selman@cs. cornell. edu Module Probability --- Part b) Bayes’ Rule Random Variables 1

Bayes’ Theorem How to assess the probability that a particular event will occur on the basis of partial evidence? Examples: What is the likelihood that people who test positive to a particular disease (e. g. , HIV), actually have the disease? What is the probability that an e-mail message is spam? Key idea: one should factor in additional information regarding occurrence of events. 2

Assume that with respect to events F and E (“E” for “Evidence”): We know P(F) – probability that event F occurs (e. g. probability that email message is spam; this is given by what fraction of email is spam) We also know event E has occurred. (e. g. , email message contains words “sale” and “bargain”) Therefore the probability conditional probability that F occurs given that E occurs, P(F|E), is a more realistic estimate that F occurs than P(F). How do we compute P(F|E)? E. g. , based on P(F), P(E|F), and P(E| ¬F) Note: ¬F is also referred to as complement of F (FC or F).
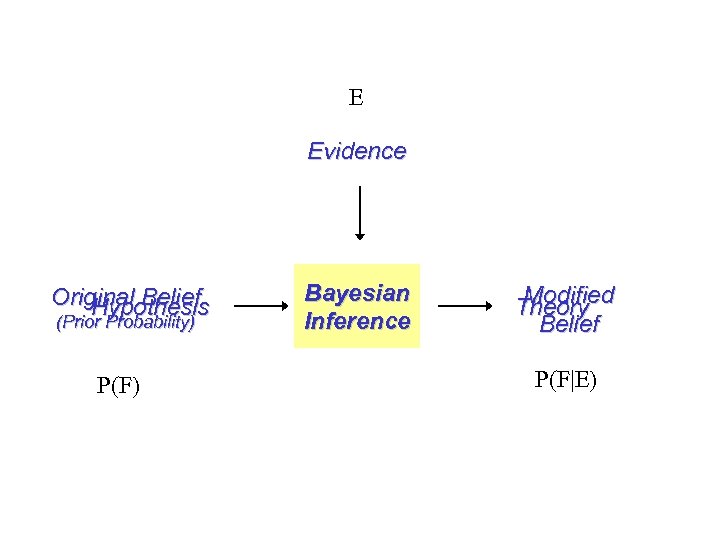
E Evidence Original Belief Hypothesis (Prior Probability) P(F) Bayesian Inference Modified Theory Belief P(F|E)
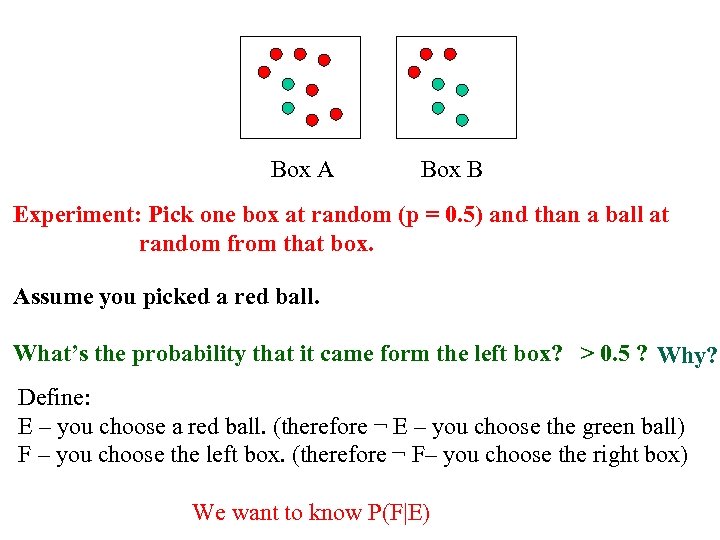
Box A Box B Experiment: Pick one box at random (p = 0. 5) and than a ball at random from that box. Assume you picked a red ball. What’s the probability that it came form the left box? > 0. 5 ? Why? Define: E – you choose a red ball. (therefore ¬ E – you choose the green ball) F – you choose the left box. (therefore ¬ F– you choose the right box) We want to know P(F|E)
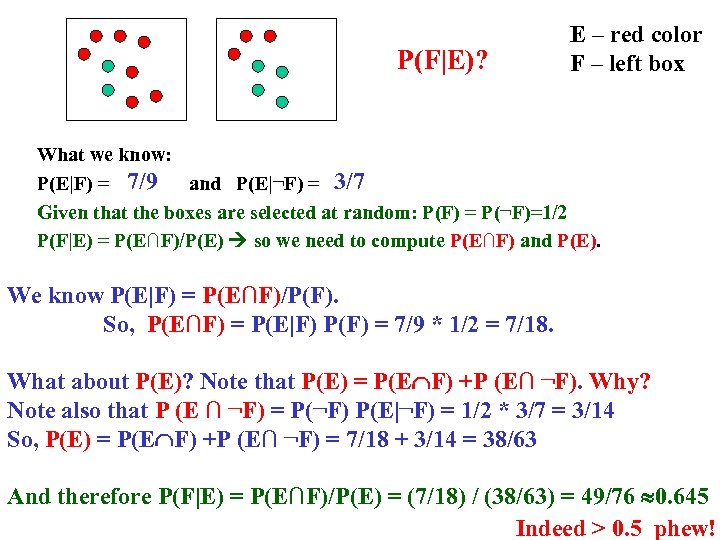
P(F|E)? E – red color F – left box What we know: P(E|F) = 7/9 and P(E|¬F) = 3/7 Given that the boxes are selected at random: P(F) = P(¬F)=1/2 P(F|E) = P(E∩F)/P(E) so we need to compute P(E∩F) and P(E). We know P(E|F) = P(E∩F)/P(F). So, P(E∩F) = P(E|F) P(F) = 7/9 * 1/2 = 7/18. What about P(E)? Note that P(E) = P(E F) +P (E∩ ¬F). Why? Note also that P (E ∩ ¬F) = P(¬F) P(E|¬F) = 1/2 * 3/7 = 3/14 So, P(E) = P(E F) +P (E∩ ¬F) = 7/18 + 3/14 = 38/63 And therefore P(F|E) = P(E∩F)/P(E) = (7/18) / (38/63) = 49/76 0. 645 Indeed > 0. 5 phew!
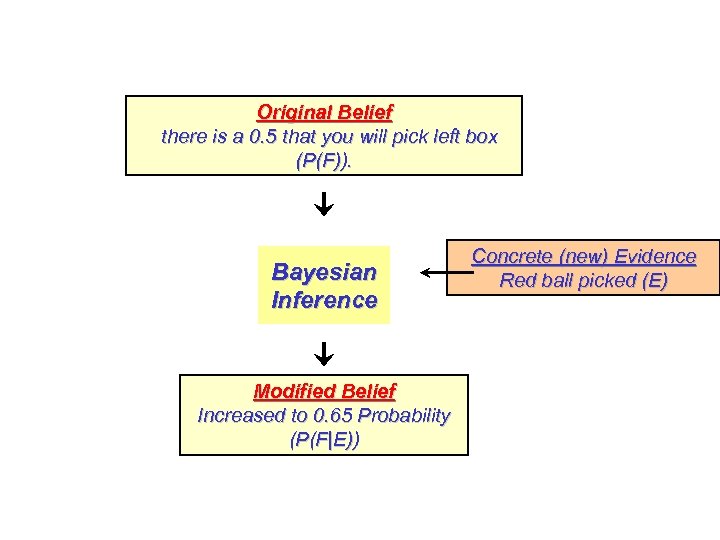
Original Belief there is a 0. 5 that you will pick left box (P(F)). Bayesian Inference Modified Belief Increased to 0. 65 Probability (P(F|E)) Concrete (new) Evidence Red ball picked (E)

Theorem: Bayes’ Theorem Suppose that E and F are events from a sample space S such that P(E) ≠ 0 and P(F)≠ 0. Then Proof:

Example --- A Classic! Suppose that 1 person in 100, 000 has a particular rare disease. There is an good test for the disease that is correct in 99% of the time when given to someone with the disease; it is correct in 99. 5% of the time when given to someone without the disease. Find: a) Probability that someone who tests positive has the disease. b) Probability that someone who tests negative does not have the disease.

1 person in 100, 000 has rare disease. Test correct in 99% of the time when given to someone with the disease; correct in 99. 5% of the time Always start by defining the events! when given to someone without the disease. Solution: a) F – the person has the disease E – the person tests positive to the disease P(F|E) – probability of having the disease given positive test P(F)=1/100, 000 = 0. 00001; P(FC) = 0. 99999 Why these probabilities? Most easily measured! P(E|F) = 0. 99; P(EC|F) = 0. 01 P(E|FC) = 0. 005 Only 0. 2% of people who test positive actually have the disease!!! Counter –intuitive. That’s why it’s a classic! (note: test is good the disease is rare; but context matters. )

b) F – the person has the disease E – the person tests positive to the disease P(FC|EC) – probability of not having the disease given negative test P(F) = 1/100, 000 = 0. 00001; P(FC) = 0. 99999 P(E|F) = 0. 99; P(EC|F) = 0. 01 P(E|FC) = 0. 005 That’s… pretty good!

Generalized Bayes’ Theorem Suppose that E is an event from a sample space S and F 1, F 2 , …, Fn are mutually exclusive events such that Asume that P(E) ≠ 0 and P(Fi) ≠ 0 for i=1, 2, …, n. Then Compare: P(E)

Bayesian Spam Filters 17 17

Applying Bayes’ Theorem: SPAM or HAM? Let our sample space or universe be the set of emails. (So, we’re sampling from the space of possible emails. ) Let S be the event a message is spam; hence is the event a message is not spam Let E be the event a message contains a word w. Since we have no idea of likelihood of SPAM, we assume P(S)=P(SC)=1/2. How do we get and Can we do better? ? 18

Estimations Note these are estimates based on frequencies in samples. 19 19

Estimation Continued So, becomes So, what do we want for p(w) and q(w) ? ? What’s the max prob and what’s the min? When do we get 0. 5? So, a quite straightforward formula for our first Bayesian spam filter! Note P(S) = P(SC) = ½ divides 20

Spam based on single words? Probabilities based on single words: Bad Idea – False positives AND false negatives a plenty Calculate based on n words, assuming each event Ei|S (Ei|SC) is independent (not true but reasonable approximation) P(S) = P(SC). Derivation see Sect. 6. 3. 21 21

Final Approximation Compare to single word: 22 22

How do we use this? User must train the filter based on messages in his/her inbox to estimate probabilities. The program or user must define a threshold probability r: If , the message is considered spam. Gmail: Train on all users! (note: report spam button) 23 23

Example Suppose the filter has the following data Threshold Probability: . 9 “Nigeria” occurs in 250 of 2000 spam messages “Nigeria” occurs in only 5 of 1000 non-spam messages Let’s try to estimate the probability, using the process we just defined 24 24

Example Cont. Step 1: Find the probability that the message has the word “Nigeria” in it and is spam. – p(Nigeria) = 250 / 2000 = 0. 125 Step 2: Find the probability that the message has the word “Nigeria” in it and is not spam. – q(Nigeria) = 5 / 1000 = 0. 005 25 25

Example Cont. Since we are assuming that it is equally likely that an incoming message is or is not spam, we can estimate the probability with this equation: r(Nigeria) = p(Nigeria) + q(Nigeria) 26 26

Example Cont. 0. 125____ 0. 125 + 0. 005 = 0. 125 0. 130 = 0. 962 Since r(Nigeria) is greater than the threshold of 0. 9, we can reject this message as spam. 27 27

Multiple Words 2000 Spam messages; 1000 real messages “Nigeria” appears in 400 spam messages “Nigeria” appears in 60 real messages “bank” appears in 200 spam and 25 real messages Threshold Probability: . 9 Let’s calculate the probability that message with “Nigeria” and “bank” is spam. 28 28

Example Cont. Step 1: Find the probability that the message has the word “Nigeria” in it and is spam. – p(Nigeria) = 400 / 2000 = 0. 2 Step 2: Find the probability that the message has the word “Nigeria” and is not spam. – q(Nigeria) = 60 / 1000 = 0. 06 Step 3: Find the probability that the message contains the word “bank” and is spam. – p(bank) = 200 / 2000 = 0. 1 Step 4: Find the probability that the message contains the word “bank” and is not spam. – q(bank) = 25 / 1000 = 0. 025 29

Example Cont Using our approximation, we have: r(Nigeria, bank) = p(Nigeria) * p(bank) + q(Nigeria) * q(bank) 30 30

Example Cont. Using our approximation, we have: r(Nigeria, bank) = p(Nigeria) * p(bank) + q(Nigeria) * q(bank) r(Nigeria, bank) = (0. 2)(0. 1) + (0. 6)(0. 025) = 0. 930 This message will be rejected however since we set the threshold probability at 0. 9. Concludes Bayes Reasoning 31 31

Probability Paradox I 32

C Magic Dice: Or How to Win Every Time! D a) You select any one of the four dice (A, B, C, or D). b) I’ll select another. Both dice are thrown, highest number wins throw. Do series of 10 throws. The person with the most highest throws wins the series. (I. e. die “more likely to get a higher number” wins. ) B A Claim: In a game of 'The Best of Ten Throws’, I will almost certainly win --- no matter which die you pick!! Why is this strange? Say, you pick die A. Let’s assume, die B is better. So, I pick B. But, then, next game & next person picks B. Let’s assume C is better. I’ll select C. Next person, will pick C. I’ll pick D. But, could such a set of Next person, will pick D… Hmm… ? ? dice exist? I’ll pick A and will win!! A < B < C < D …. < A !! Failure of transitivity! Surprisingly, yes!
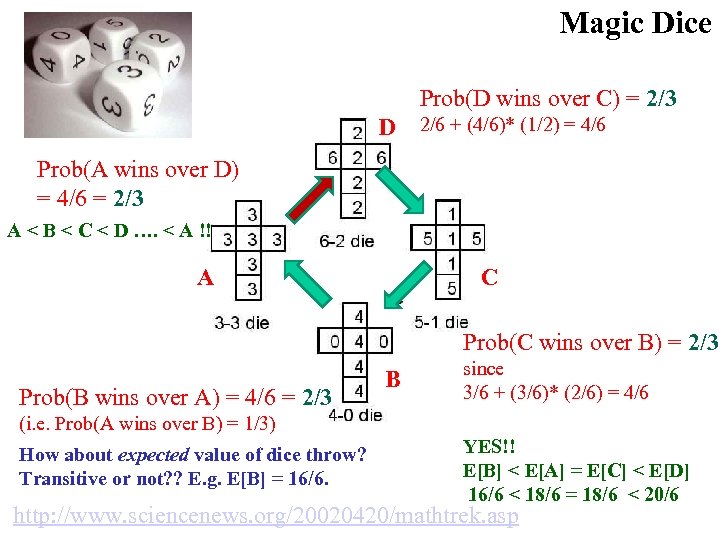
Magic Dice Prob(D wins over C) = 2/3 D 2/6 + (4/6)* (1/2) = 4/6 Prob(A wins over D) = 4/6 = 2/3 A < B < C < D …. < A !! A C Prob(C wins over B) = 2/3 Prob(B wins over A) = 4/6 = 2/3 B since 3/6 + (3/6)* (2/6) = 4/6 (i. e. Prob(A wins over B) = 1/3) How about expected value of dice throw? Transitive or not? ? E. g. E[B] = 16/6. YES!! E[B] < E[A] = E[C] < E[D] 16/6 < 18/6 = 18/6 < 20/6 http: //www. sciencenews. org/20020420/mathtrek. asp

Random Variables and Distributions 35

Random Variables For a given sample space S, a random variable (r. v. ) is any real valued function on S, i. e. , a random variable is a function that assigns a real number to each possible outcome Numbers Sample space S -2 0 Suppose our experiment is a roll of 2 dice. S is set of pairs. Example random variables: X = sum of two dice. X((2, 3)) = 5 Y = difference between two dice. Y((2, 3)) = 1 Z = max of two dice. Z((2, 3)) = 3 2

Random variable Suppose a coin is flipped three times. Let X(t) be the random variable that equals the number of heads that appear when t is the outcome. X(HHH) = 3 X(HHT) = X(HTH) = X(THH) = 2 X(TTH) = X(THT) = X(HTT) = 1 X(TTT) = 0 Note: we generally drop the argument! We’ll just say the “random variable X” (even though it’s technically a function). And write e. g. P(X = 2) for “the probability that the random variable X(t) takes on the value 2”. Or P(X=x) for “the probability that the random variable X(t) takes on the value x. ”

Distribution of Random Variable Definition: The distribution of a random variable X on a sample space S is the set of pairs (r, p(X=r)) for all r X(S), where p(X=r) is the probability that X takes the value r. A distribution is usually described specifying p(X=r) for each r X(S). A probability distribution on a r. v. X is just an allocation of the total probability mass, 1, over the possible values of X. 38

The Birthday Paradox 41

A: 23 Birthdays a) 23 How many people have to be in a room to assure that the probability that at least two of them have the same birthday is greater than 1/2? b) 183 c) 365 d) 730 Let pn be the probability that no people share a birthday among n people in a room. Then 1 - pn is the probability that 2 or more share a birthday. We want the smallest n so that 1 - pn > 1/2. For L options answer is in the order of sqrt(L) ? Informally, why? ? Hmm. Why does such an n exist? Upper-bound?

Birthdays Assumption: Birthdays of the people are independent. Each birthday is equally likely and that there are 366 days/year Let pn be the probability that no-one shares a birthday among n people in a room. What is pn? (“brute force” is fine) Assume that people come in certain order; the probability that the second person has a birthday. Different than the first is 365/366; the probability that the third person has a different birthday. Form the two previous ones is 364/366. . For the jth person we have (366 -(j-1))/366.

So, After several tries, when n=22 1= pn = 0. 475. n=23 1 -pn = 0. 506 Relevant to “hashing”. Why?

Probability of a Collision in Hashing Functions A hashing function h(k) is a mapping of the keys (or records, e. g. , SSN, around 300 x 106 in the US) to a much smaller storage location. A good hashing fucntion yields few collisions. What is the probability that no two keys are mapped to the same location by a hashing function? Assume m is the number available storage locations, so the probability of mapping a key to a location is 1/m. Assuming the keys are k 1, k 2, kn, the probability of mapping the jth record to a free location is after the first (j-1) records is (m-(j-1))/m. From Birthday Problem to Hashing Functions Given a certain m, find the smallest n Such that the probability of a collision is greater than a particular threshold p. It can be shown that for p>1/2, n 1. 177 m = 10, 000, gives n = 117. Not that many! 45
87fba237d25c889153b6eb817e4b8ef5.ppt