Disclosure Limitation Methods and Information Loss for Tabular

Disclosure Limitation Methods and Information Loss for Tabular Data George T. Duncan, Stephen E. Fienberg, Ramayya Krishnan, Rema Padman and Stephen F. Roehrig Carnegie Mellon University

Focus of the Talk • Categorical data: – Compilations of surveys and other data gathering efforts – Tables of counts (e. g. , number of females in Metropolis with income > $200, 000) – Cf. microdata • Does the release of a table allow inference of a sensitive attribute value for an individual (e. g. , Lois Lane’s income)? – Exact value – Range of values – Probability distribution

Some Tough Questions • Exact, interval or probabilistic disclosure? • Should we analyze a data product in isolation? Or must we look at the suite of products released? • Longitudinal data can be especially revealing. How can we know next year’s data? • What about linkage with external data sources? Are we responsible for everything that’s out there?

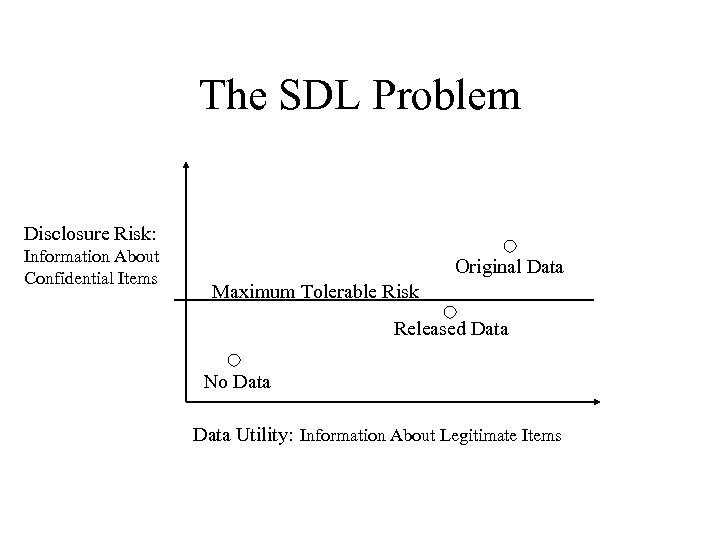
The SDL Problem Disclosure Risk: Information About Confidential Items Original Data Maximum Tolerable Risk Released Data No Data Utility: Information About Legitimate Items

Risk and Utility • Disclosure risk depends on – The definition of disclosure, and – The ways disclosure could occur. • Data utility is – A measure of information loss, and – Maximal for the original data. • Often we can trade off disclosure risk and data utility

Sample Measure for Risk • Risk for a cell is where – r(k) is the risk of a snooper discovering cell value is k – p(k) is the probability of the cell having value k. • The agency determines r(k), then tries to estimate the snooper’s posterior for p(k), given the table release.

Sample Measures for Utility • Cell-oriented: mean square precision of the user’s posterior distribution for a cell. • Table-oriented: change in 2 for 2 -way tables, other (or multiple) measures of association for n-way tables.

Disclosure Auditing • “Traditional” risk assessment • A data disseminator follows these steps: – Audit a proposed release for disclosures – If potential disclosures exist , apply SDL – Audit the result to ensure protection – Repeat as necessary • Once more, what is a disclosure?

Disclosure Auditing (cont. ) • Disclosure may be a sensitive cell value known – with certainty, – to be in a narrow range, or – with high probability. • Let’s examine some SDL techniques, considering – – The various definitions of disclosure, The difficulty of applying and auditing them, The utility of the disclosure-limited results, and Whether they are useful for higher-dimensional tables.

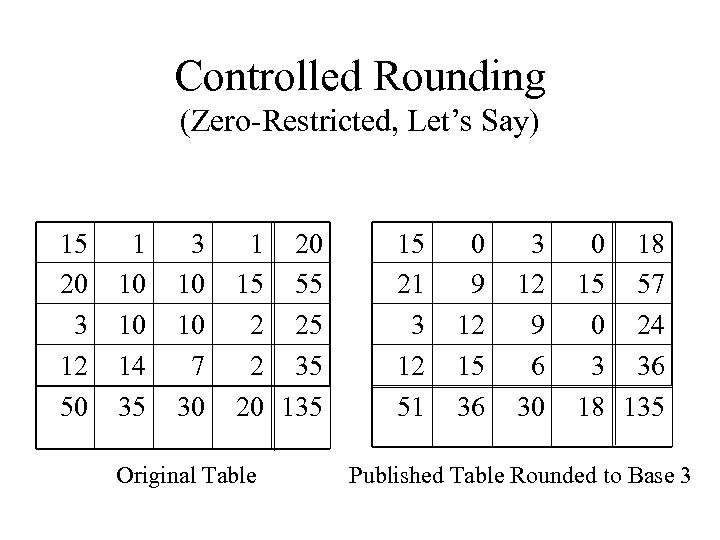
Controlled Rounding (Zero-Restricted, Let’s Say) 15 20 3 12 50 1 10 10 14 35 3 10 10 7 30 1 20 15 55 2 25 2 35 20 135 Original Table 15 21 3 12 51 0 9 12 15 36 3 12 9 6 30 0 18 15 57 0 24 3 36 18 135 Published Table Rounded to Base 3

Controlled Rounding (cont. ) • No exact disclosures can occur. • The “feasibility interval” of any cell is its published value ± (b-1), where b is the rounding base (except close to zero). • Finding a rounding is easy for 2 -way tables. • Finding a rounding is harder (and may not even exist) for higher-dimensional tables.

Controlled Rounding (cont. ) • There are 576, 598, 396 tables that could be rounded to the published table. • How to determine a prior probability over this set? • With a huge leap of faith about priors, cell (1, 2) has this distribution: q Pr(q) 0. 436 1. 347 2. 217

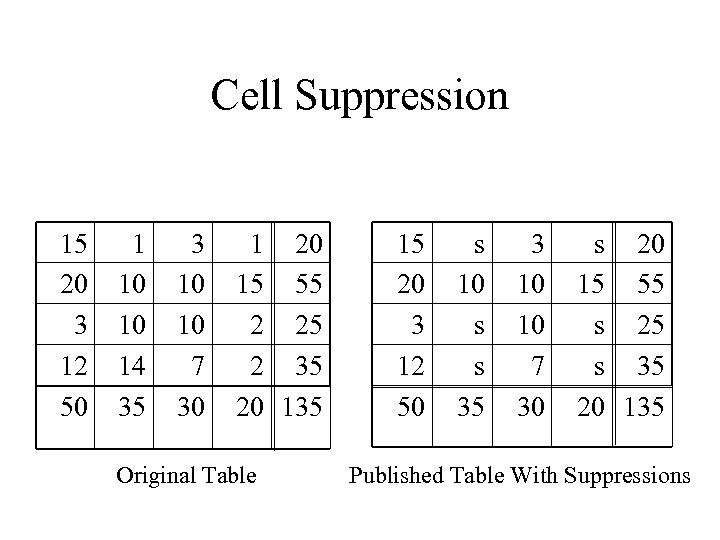
Cell Suppression 15 20 3 12 50 1 10 10 14 35 3 10 10 7 30 1 20 15 55 2 25 2 35 20 135 Original Table 15 20 3 12 50 s 10 s s 35 3 10 10 7 30 s 20 15 55 s 25 s 35 20 135 Published Table With Suppressions

Cell Suppression (cont. ) • Finding a suppression pattern can be hard computationally; heuristics may be untrustworthy. • Auditing is often done with linear programming (LP), finding upper and lower cell bounds. • In higher dimensions, LP may give fractional bounds---how to interpret? • How does an analyst use a table with suppressions?

Cell Suppression (cont. ) • Again, there are many possible true tables. – For 2 -way tables, they are easily enumerated. – For n-way tables, it’s quite hard. • Again, it’s difficult to specify priors (need to know the exact implementation of suppression algorithm). • Posterior distributions for suppressed cells can be had, but it’s a lot of work.

Publishing Only Some Margins of an N-Way Table • Think of the n-way “base table” as being fully suppressed. • The published marginal tables constrain the values in the base table. • Auditing characterizes cells in the base table and/or other unpublished margins. • Here’s an example:

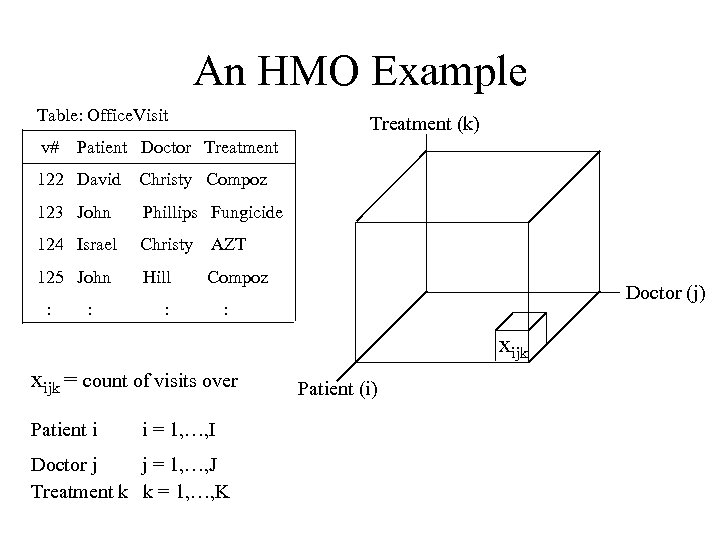
An HMO Example Table: Office. Visit v# Treatment (k) Patient Doctor Treatment 122 David Christy Compoz 123 John Phillips Fungicide 124 Israel Christy AZT 125 John Hill Compoz : : : Doctor (j) : xijk = count of visits over Patient i i = 1, …, I Doctor j j = 1, …, J Treatment k k = 1, …, K Patient (i)

The HMO Example (cont. ) • Obviously we don’t broadcast Patient-Doctor. Treatment. • The view Patient-Treatment is also sensitive. • But the Accounting Dept. has Patient-Doctor. • And the Physician Review Board has Doctor. Treatment. • Ted works in Accounting, his wife Alice is on the Physician Review Board, and Israel is an occasional babysitter for them.

More Generally • An n-way table of sensitive data. • Some collection of lower-dimensional marginal tables are proposed for publication. • How to find bounds, or better, distributions, for the sensitive cells? • Recall linear programming often gives fractional bounds.

Integer Linear Programming? • Many techniques, but generally very slow compared to continuous LP. • Empirically, “Gomory cuts” work well. • Some special problems have the “integer rounding property. ” • Much more to be done here.

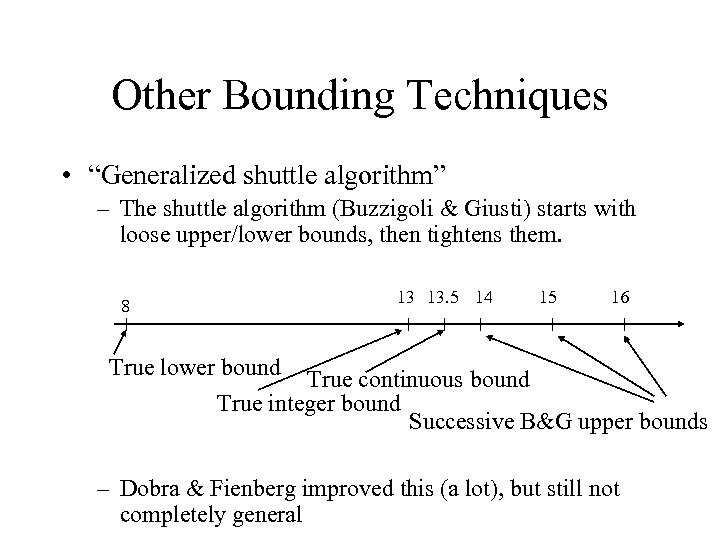
Other Bounding Techniques • “Generalized shuttle algorithm” – The shuttle algorithm (Buzzigoli & Giusti) starts with loose upper/lower bounds, then tightens them. 8 13 13. 5 14 15 16 True lower bound True continuous bound True integer bound Successive B&G upper bounds – Dobra & Fienberg improved this (a lot), but still not completely general

Exploiting Structure • Decomposable graphs – Suppose 3 -D table (indices I, J, K), we publish IJ+ and +JK, and want bounds for IJK. – The Dobra-Fienberg graph looks like: I J K +JK IJ+ – Dobra and Fienberg show that if the graph has a separator (node J), and this separator is a clique, then Frechet bounds are exact.

Probabilities of Cell Values • Diaconis and Sturmfels (1998) show to sample from the space of tables that agree with known marginals. • Not hard to extend to tables with suppressions. • They use results from commutative algebra to find a “Gröbner basis”, a list of moves that change a table but leave the margins fixed. • A random walk using these moves carries you uniformly thorough the space of tables. • Tally the proportion of time a sensitive cell takes on different values.

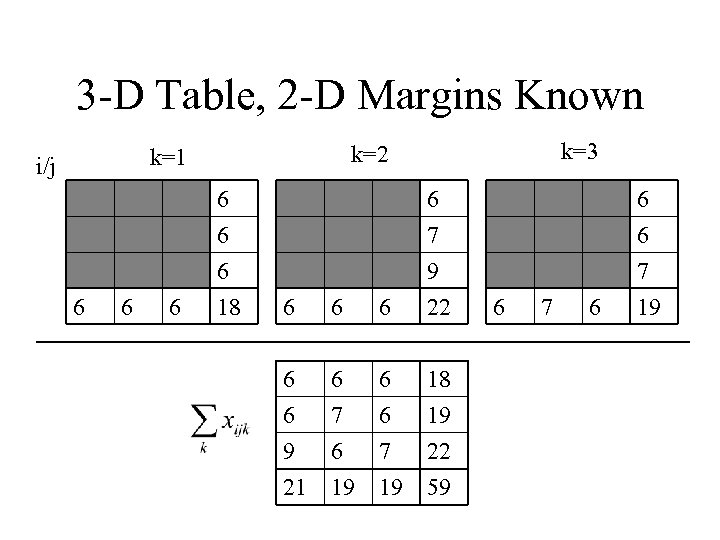
3 -D Table, 2 -D Margins Known i/j 6 6 6 k=3 k=2 k=1 6 6 6 18 6 6 7 9 22 6 6 9 21 6 7 6 19 6 6 7 19 18 19 22 59 6 7 6 6 6 7 19

Gröbner Bases “Moves” • Suppose we know a table that matches the published margins (i. e. , is feasible). • How can we move to another feasible table? • Example move: + 0 + 0 0 0 0 0

Computing the Gröbner Basis • The general-purpose program Macauley can find the 3 3 3 basis in about 7 hours (300 MHz PC). • A specialized program does this in 25 m. S. • The 4 3 3 basis takes 20 minutes (628 moves) • The 5 3 3 basis takes 3 months (3236 moves)…

Exploiting Structure Again • If the independence graph of the released marginals is decomposable, the Gröbner basis is easily determined. • If the graph is “almost” decomposable, the basis can be obtained by piecing together bases for smaller problems. • Dobra demonstrates that these methods can be used to estimate sensitive cell distributions.

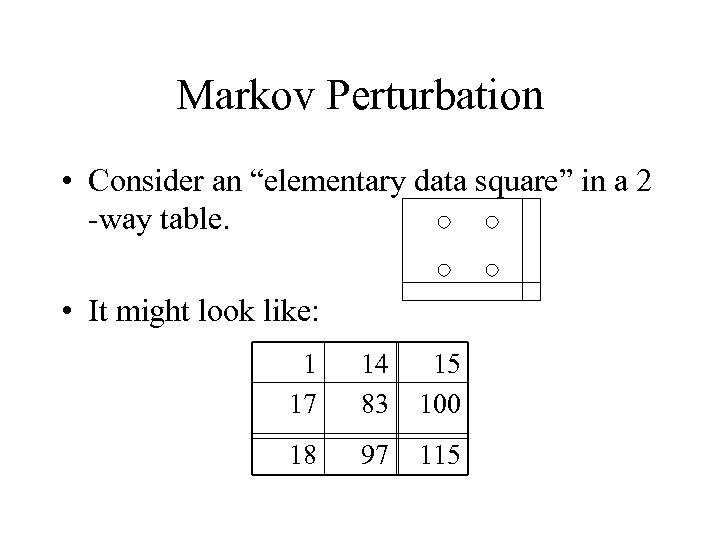
Markov Perturbation • Consider an “elementary data square” in a 2 -way table. • It might look like: 1 17 14 83 15 100 18 97 115

Markov Perturbation (cont. ) • The cell values in the data square stochastically modified so that – the marginal totals remain unchanged, and – the expected cell values equal the original values (unbiased). • A single parameter determines how much “mixing” is done. • By choosing elementary data squares randomly, then perturbing, the overall table is protected.

Markov Perturbation (cont. ) • In the book chapter, we show a Bayesian analysis comparing – Markov perturbation – Cell suppression, and – Rounding. • The resulting Risk-Utility Confidentiality Map shows some of the trade-offs in choosing a SDP method.

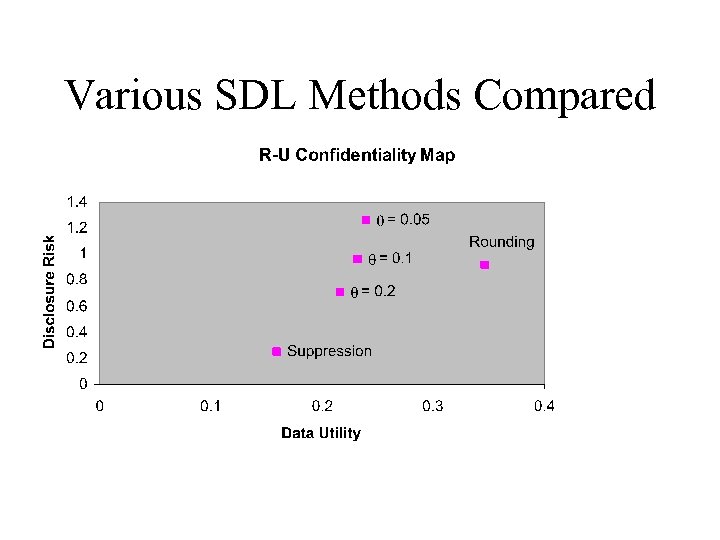
Various SDL Methods Compared

Directions for Research • Distributions of cell values in protected tables. • Examining the consequences of different user/intruder prior distributions on SDL method tradeoffs. • New procedures with increased data utility while maintaining low risk. • All of this for higher-dimensional tables.