Дисциплина ВВЕДЕНИЕ В ФИЗИКУ Преподаватель Пацева Юлия Владимировна

Дисциплина «ВВЕДЕНИЕ В ФИЗИКУ» Преподаватель: Пацева Юлия Владимировна, patzeva@mail. ru Кафедра: «Физика» , 526 ауд. гл. к. Составляющие курса: Лекции - 6 часов, Практические занятия – 8 часов, Форма итоговой аттестации – зачет/экзамен. К зачету/экзамену допускаются студенты: Выполнившие 1 домашнюю контрольную работу. Крайний срок сдачи контрольной работы 20 мая.

Литература: 1 Учебники: Тpофимова Т. И. Куpс физики 2 Савельев И. В. Курс общей физики в 5 кн. / кн. 1: Механика 3 Савельев И. В. Курс общей физики в 5 кн. / кн. 3: Молекулярная физика и термодинамика 4 Савельев И. В. Курс общей физики : в 4 т. — Т. 1. Механика. Молекулярная физика и термодинамика Дополнительные пособия: 1 Тpофимова Т. И. Справочник по физике для студентов и абитуриентов 2 Жуковская Т. М. , Полетаев Г. М. , Пацева Ю. В. , Науман Л. В. Учебнометодическое пособие по решению задач по физике. Часть I. Механика: для студентов всех форм обучения 3 Тpофимова Т. И. , Павлова З. Г. Сборник задач по курсу физики решениями с

Тема 1 Кинематика и динамика материальной точки и твердого тела - Основные кинематические характеристики криволинейного движения: скорость и ускорение. Нормальное и тангенциальное ускорение. Кинематика вращательного движения: угловая скорость и угловое ускорение, их связь с линейной скоростью и ускорением. - Законы Ньютона. Уравнение движения материальной точки. Силы в механике. - Момент силы. Момент импульса материальной точки и механической системы. Момент инерции. Теорема Штейнера. Основное уравнение динамики вращательного движения твердого тела.

0 Понятие механики, модели в механике Механика – часть физики, которая изучает закономерности механического движения и причины, вызывающие или изменяющие это движение. Механическое движение – это изменение с течением времени взаимного расположения тел или их частей. Механика подразделяется на три части: статику, кинематику и динамику.

Кинематика (от греч. «kinema» – движение) – раздел механики, в котором изучаются геометрические свойства движения тел без учета их массы и действующих на них сил. Динамика (от греч. «dynamis» – сила) изучает движения тел в связи с теми причинами, которые обуславливают это движение. Статика (от греч. «statike» – равновесие) изучает условия равновесия тел. Поскольку равновесие – есть частный случай движения, законы статики являются естественным следствием законов динамики и в данном курсе не изучается.

Без знаний механики невозможно представить себе развитие современного машиностроения. Развитие механики, как науки, начиналось с III в. до н. э. , когда древнегреческий ученый Архимед (287 – 312 до н. э. ) сформулировал закон рычага и законы равновесия плавающих тел. Основные законы механики установлены итальянским физиком и астрономом Г. Галилеем (1564 – 1642) и окончательно сформулированы английским физиком И. Ньютоном (1643 – 1727). Механика Галилея и Ньютона называется классической, т. к. она рассматривает движение макроскопических тел со скоростями, значительно меньшими скорости света в вакууме.

Для описания движения тел в зависимости от условий задачи используют различные физические модели: - Тело, деформацией которого можно пренебречь в условиях данной задачи, называют абсолютно твердым телом (хотя абсолютно твердых тел в природе не существует). - Тело, размерами которого в условиях данной задачи, можно пренебречь, называется материальной точкой.

1 Система отсчета, тело отсчета Всякое движение относительно, поэтому для описания движения необходимо условиться, относительно какого другого тела будет отсчитываться перемещение данного тела. Выбранное для этой цели тело называют телом отсчета. Практически, для описания движения приходится связывать с телом отсчета систему координат (декартова, сферическая).

Система отсчета – совокупность системы координат и часов, связанных с телом отсчета по отношению к которому изучается движение. Движения тела, как и материи, вообще не может быть вне времени и пространства. Материя, пространство и время неразрывно связаны между собой (нет пространства без материи и времени и наоборот).

Пространство трехмерно, поэтому «естественной» системой координат является, декартова или прямоугольная система координат, которой мы в основном и будем пользоваться. В декартовой системе координат, положение точки М в данный момент времени по отношению к этой системе характеризуется тремя координатами x, y, z или радиус-вектором , проведенным из начала координат в данную точку М.

При движении материальной точки её координаты с течением времени изменяются. В общем случае её движение определяется кинематическими уравнениями движения: (1) Эти уравнения эквивалентны векторному уравнению: (2) на где х, у, z – проекции радиус-вектора оси координат, а i, j, k – единичные векторы (орты), направленные по соответствующим осям.

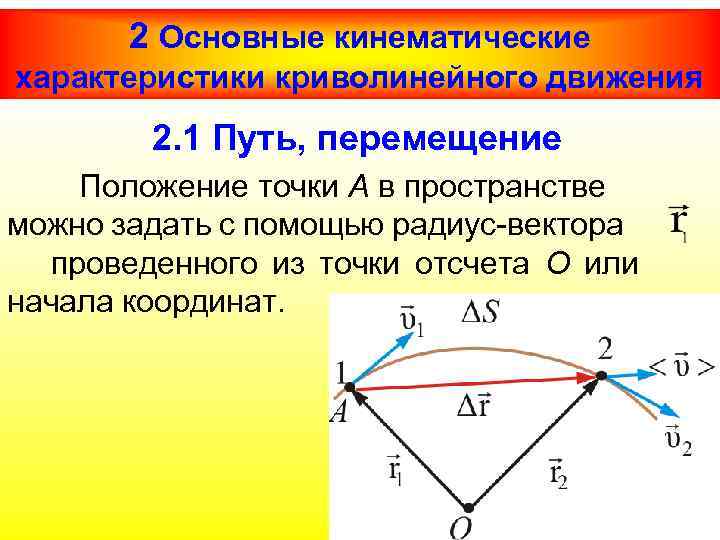2 Основные кинематические характеристики криволинейного движения 2. 1 Путь, перемещение Положение точки А в пространстве можно задать с помощью радиус-вектора проведенного из точки отсчета О или начала координат.

При движении точки А из точки 1 в точку 2 её радиусвектор изменяется и по величине, и по направлению, т. е. зависит от времени t. Геометрическое место точек концов называется траекторией точки. Длина траектории - путь ΔS. Если точка движется по прямой, то приращение равно пути S.

Пусть за время t точка А переместилась из точки 1 в точку 2. Вектор перемещения приращение за время t - это

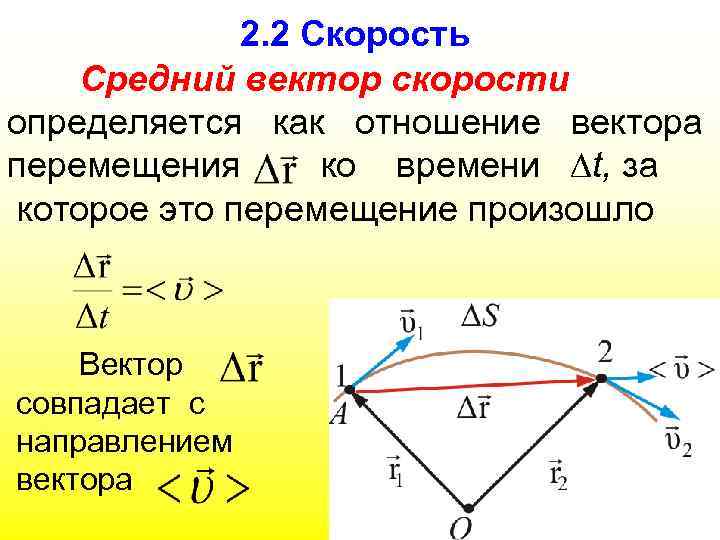2. 2 Скорость Средний вектор скорости определяется как отношение вектора перемещения ко времени t, за которое это перемещение произошло Вектор совпадает с направлением вектора

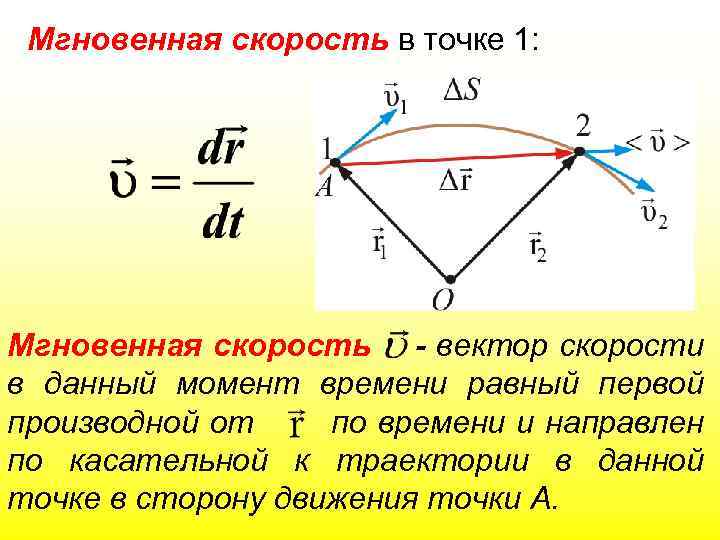Мгновенная скорость в точке 1: Мгновенная скорость - вектор скорости в данный момент времени равный первой производной от по времени и направлен по касательной к траектории в данной точке в сторону движения точки А.

Модуль вектора скорости: При t 0 т. е. на бесконечно малом участке траектории S = r (перемещение совпадает с траекторией). В этом случае мгновенную скорость можно выразить через скалярную величину – путь: S – скаляр.

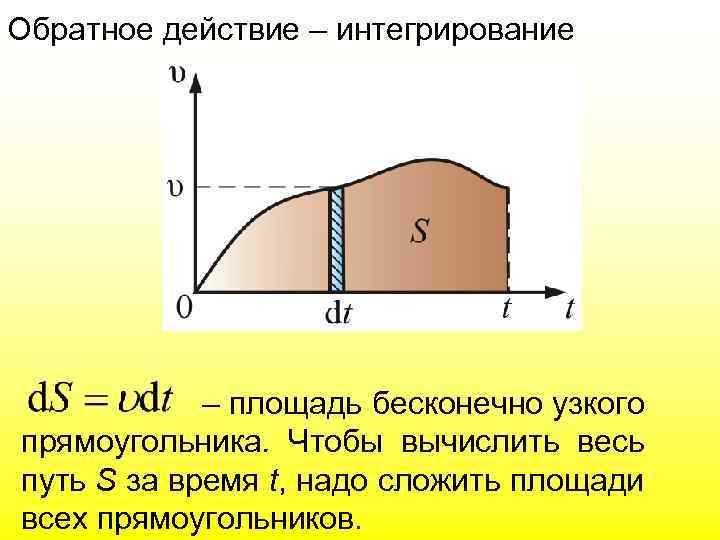Обратное действие – интегрирование – площадь бесконечно узкого прямоугольника. Чтобы вычислить весь путь S за время t, надо сложить площади всех прямоугольников.

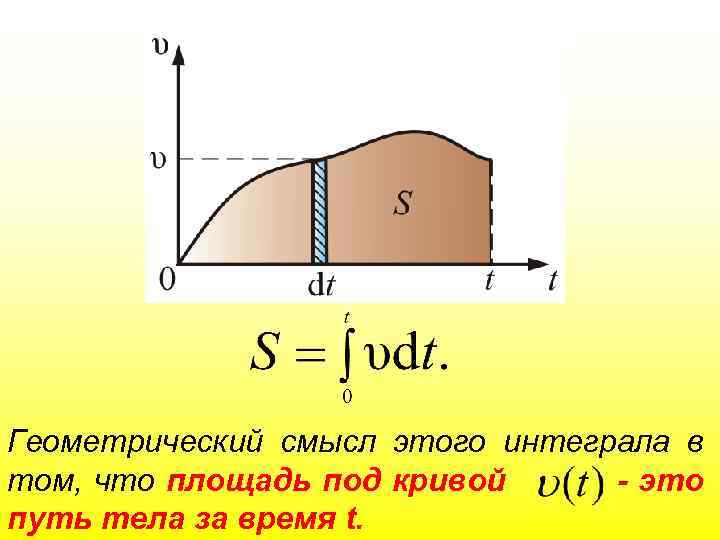Геометрический смысл этого интеграла в том, что площадь под кривой - это путь тела за время t.

Принцип независимости движения Если материальная точка участвует в нескольких движениях, то ее результирующее перемещение равно векторной сумме перемещений, обусловленных каждым из этих движений в отдельности:

Так как Тогда Таким образом, скорость тоже подчиняется принципу независимости движения.

В физике существует общий принцип, который называется принцип суперпозиций (принцип наложения), согласно которому результирующий эффект сложного процесса взаимодействия представляет собой сумму эффектов, вызываемых каждым воздействием в отдельности, при условии, что последние взаимно не влияют друг на друга. Принцип суперпозиции играет большую роль во многих разделах физики и техники.

Проекция вектора скорости на оси координат В векторной форме уравнения записываются легко и кратко. Но для практических вычислений нужно знать проекции вектора на оси координат выбранной системы отсчета. Спроецируем вектор на оси – x, y, z. х, y, z зависят от времени t, т. е. x(t), y(t), z(t). Зная зависимость этих координат от времени (закон движения точки) можно найти в каждый момент времени скорость точки.

Проекция вектора скорости равна: на ось x Здесь dx – проекция вектора перемещения на ось х. Аналогично:

Так как вектор, то где i, j, k единичные векторы – орты. Модуль вектора скорости:

2. 3 Ускорение. Нормальное и тангенциальное ускорения В произвольном случае движения скорость не остается постоянной. Быстрота изменения скорости по времени и направлению характеризуется ускорением: Ускорение величина векторная. При криволинейном движении времени, и по направлению. изменяется и по

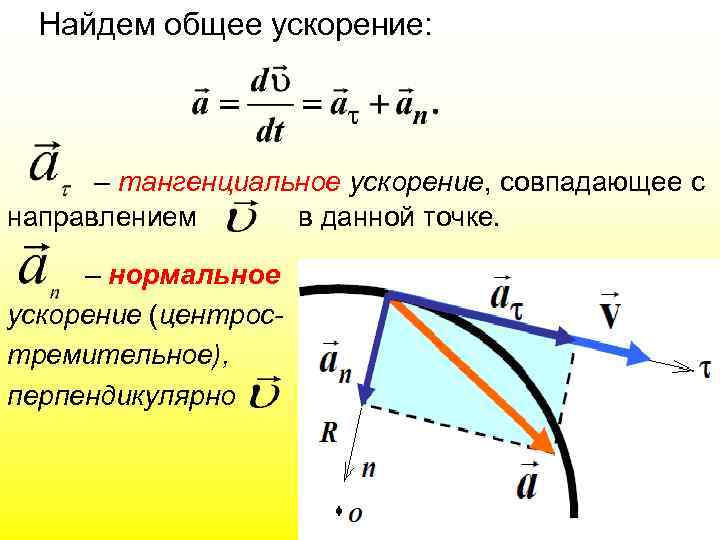Найдем общее ускорение: – тангенциальное ускорение, совпадающее с направлением в данной точке. – нормальное ускорение (центростремительное), перпендикулярно.

или по модулю характеризует изменение вектора скорости по величине: - если , то направлено в ту же сторону, что и вектор , равноускоренное движение; - если направлено в противоположную сторону - при , то , равнозамедленное движение; то , постоянной по модулю скоростью. – движение с

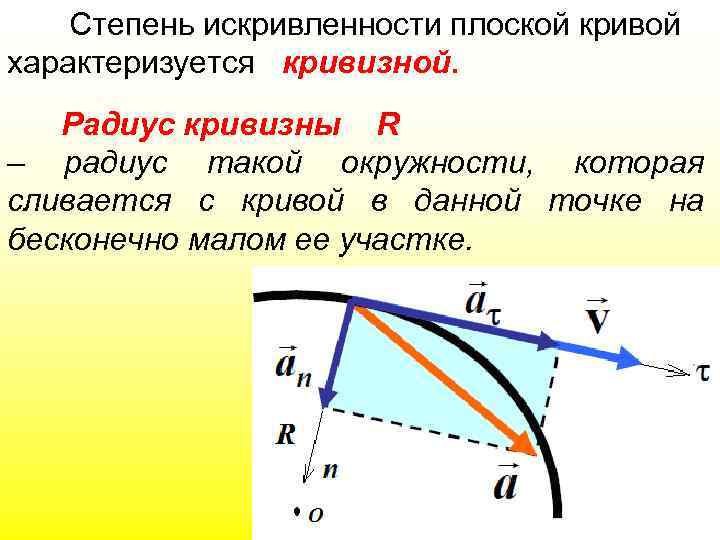Степень искривленности плоской кривой характеризуется кривизной. Радиус кривизны R – радиус такой окружности, которая сливается с кривой в данной точке на бесконечно малом ее участке.

Нормальное ускорение показывает быстроту изменения направления вектора скорости. – нормальное ускорение или центростремительное, направлено оно к центру кривизны, перпендикулярно касательной. Модуль нормального ускорения:

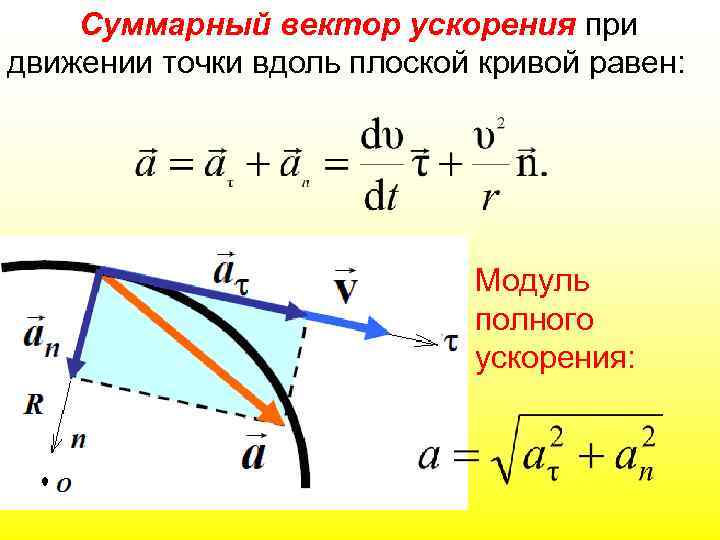Суммарный вектор ускорения при движении точки вдоль плоской кривой равен: Модуль полного ускорения:

Рассмотрим несколько предельных (частных) случаев: – равномерное прямолинейное движение; – равнопеременное прямолинейное движение; – равномерное движение по окружности.

Вспомним несколько полезных формул: При равномерном движении: При движении с постоянным ускорением (равнопеременное движение):

Обратная задача кинематики заключается в том, что по известному значению ускорения a(t) найти скорость точки и восстановить траекторию движения r(t). По определению отсюда или, так как Следовательно,

3 Кинематика твердого тела Различают два основных вида движения твердого тела: - поступательное; - вращательное вокруг оси; Остальные виды движения твердого тела можно свести к одному их этих основных видов или к их совокупности.

Поступательное движение – это движение твердого тела, при котором любая прямая, связанная с телом, остается параллельной своему начальному положению и при этом, все точки твердого тела совершают равные перемещения. Скорости и ускорения всех точек твердого тела в данный момент времени t одинаковы. Это позволяет свести изучение поступательного движения твердого тела к изучению движения отдельной точки.

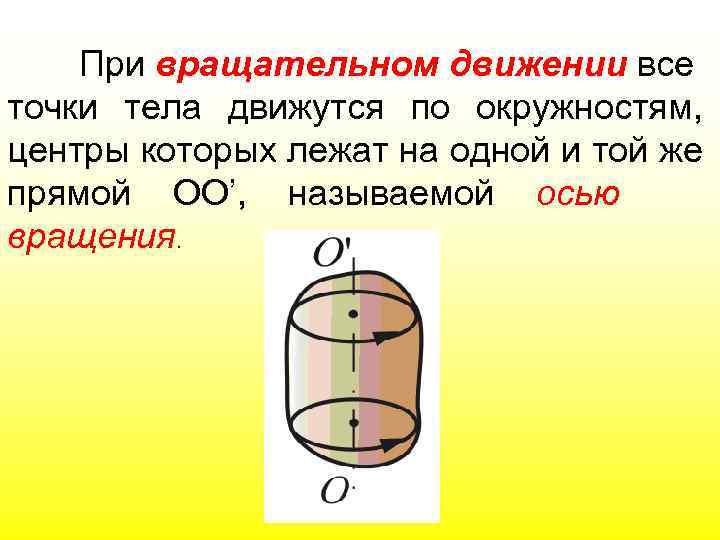При вращательном движении все точки тела движутся по окружностям, центры которых лежат на одной и той же прямой ОО’, называемой осью вращения.

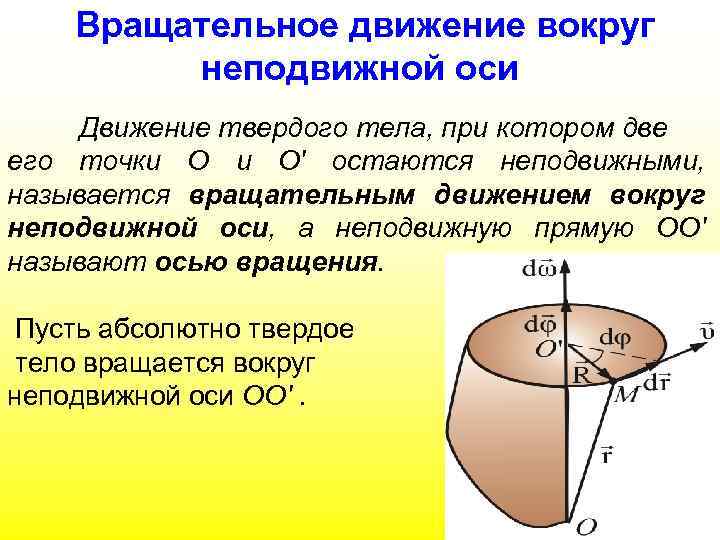Вращательное движение вокруг неподвижной оси Движение твердого тела, при котором две его точки О и О' остаются неподвижными, называется вращательным движением вокруг неподвижной оси, а неподвижную прямую ОО' называют осью вращения. Пусть абсолютно твердое тело вращается вокруг неподвижной оси ОО'.

Угол поворота характеризует угловое перемещения всего тела за время dt. Удобно ввести – вектор элементарного углового перемещения тела, численно равный и направленный вдоль оси вращения ОО' так, чтобы глядя вдоль вектора мы видели вращение по часовой стрелке (направление вектора и направление вращения связаны правилом буравчика).

Угловой скоростью называется вектор численно равный первой производной от угла поворота по времени и направленный вдоль оси вращения в направлении ( и всегда направлены в одну сторону). Модуль угловой скорости:

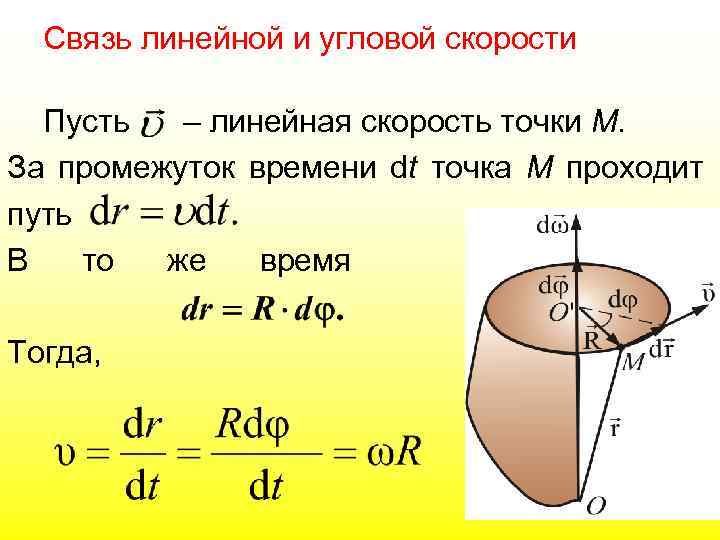Связь линейной и угловой скорости Пусть – линейная скорость точки М. За промежуток времени dt точка М проходит путь В то же время Тогда,

В векторной форме Вектор векторам ортогонален и и направлен в ту же сторону, что и векторное произведение

Период Т – промежуток времени, в течение которого тело совершает полный оборот (т. е. поворот на угол ) Частота ν – число оборотов тела за 1 сек. Угловая скорость (циклическая частота)

Введем вектор углового ускорения для характеристики неравномерного вращения тела: Вектор направлен в ту же сторону, что и при ускоренном вращении а направлен в противоположную сторону при замедленном вращении

Выразим нормальное и тангенциальное ускорения точки М через угловую скорость и угловое ускорение:

Формулы простейших случаев вращения тела вокруг неподвижной оси: - равномерное вращение - равнопеременное вращение

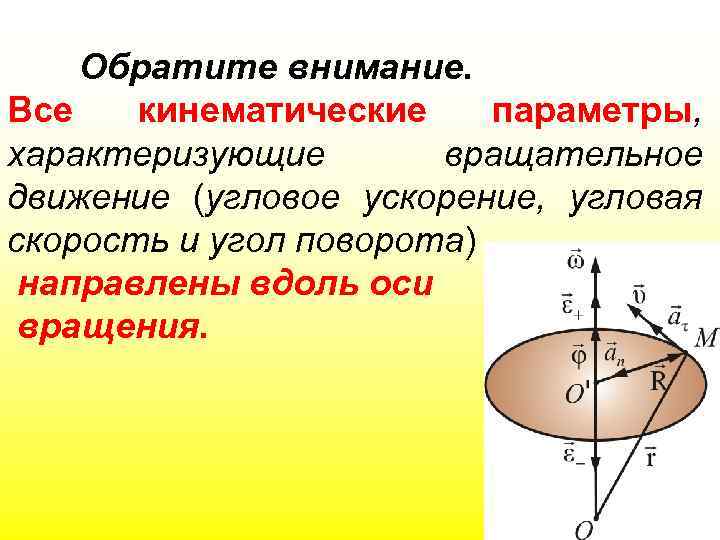Обратите внимание. Все кинематические параметры, характеризующие вращательное движение (угловое ускорение, угловая скорость и угол поворота) направлены вдоль оси вращения.

4 Законы Ньютона В основе классической или ньютоновской механики лежат три закона динамики, сформулированных И. Ньютоном в 1687 г. Эти законы играют исключительную роль в механике и являются (как и все физические законы) обобщением результатов огромного человеческого опыта.

Первый закон Ньютона: всякая материальная точка сохраняет состояние покоя или равномерного прямолинейного движения до тех пор, пока воздействие со стороны других тел не заставит её изменить это состояние. (Закон инерции)

Оба названных состояния схожи тем, что ускорение тела равно нулю. Поэтому формулировке первого закона можно придать следующий вид: скорость любого тела остаётся постоянной (в частности, равной нулю), пока воздействие на это тело со стороны других тел не вызовет её изменения. Стремление тела сохранить состояние покоя или равномерного прямолинейного движения называется инертностью. Поэтому первый закон Ньютона называют законом инерции.

Механическое движение относительно, и его характер зависит от системы отсчёта. Первый закон Ньютона выполняется не во всякой системе отсчёта, а те системы, по отношению к которым он выполняется, называются инерциальными системами отсчёта. Инерциальной системой отсчёта является такая система отсчёта, относительно которой материальная точка, свободная от внешних воздействий, либо покоится, либо движется прямолинейно и равномерно (т. е. с постоянной скоростью). Таким образом, первый закон Ньютона утверждает существование инерциальных систем отсчёта.

Система отсчёта, связанная с Землей, строго говоря, неинерциальная, однако эффекты, обусловленные её неинерциальностью (Земля вращается вокруг собственной оси и вокруг Солнца) при решении многих задач малы, и в этих случаях её можно считать инерциальной. Из приведённых выше примеров легко понять, что основным признаком инерциальной системы является отсутствие ускорения.

Масса и импульс тела Воздействие на данное тело со стороны других тел вызывает изменение его скорости, т. е. сообщает данному телу ускорение. Опыт показывает, что одинаковое воздействие сообщает разным телам разные по величине ускорения. Всякое тело противится попыткам изменить его состояние движения. Это свойство тел, как мы уже говорили, называется инертностью (следует из первого закона Ньютона). Мерой инертности тела является величина, называемая массой. Чтобы определить массу некоторого тела, нужно сравнить её с массой тела, принятого за эталон массы (или сравнить с телом уже известной массы).

Масса – величина аддитивная (масса тела равна сумме масс частей, составляющих это тело). Система тел, взаимодействующих только между собой, называется замкнутой. Рассмотрим замкнутую систему двух тел массами и. Столкнём эти два тела. (тело, обладающее большей массой, меньше изменяет скорость). Произведение массы тела на скорость называется импульсом тела.

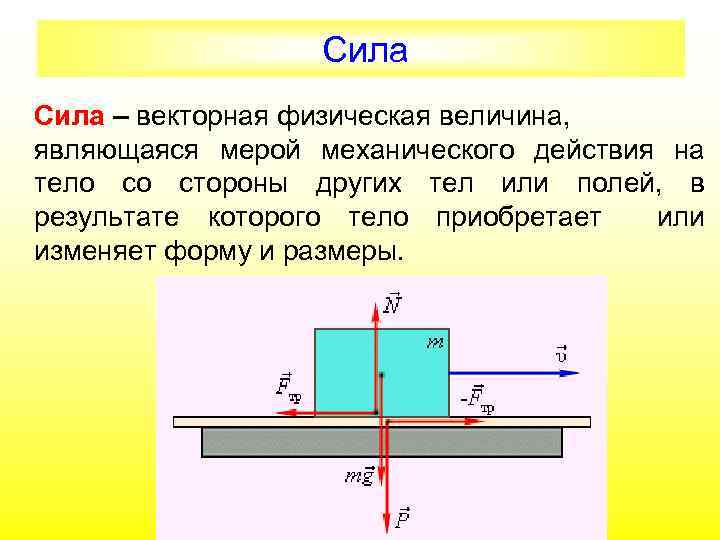Сила Cила – векторная физическая величина, являющаяся мерой механического действия на тело со стороны других тел или полей, в результате которого тело приобретает или изменяет форму и размеры.

Второй закон Ньютона Математическое выражение второго закона Ньютона: скорость изменения импульса тела равна действующей на него силе. Отсюда можно заключить, что изменение импульса тела равно импульсу силы. Получим выражение второго закона через ускорение:

- основное уравнение динамики поступательного точки. движения материальной Принцип суперпозиции или принцип независимости действия сил: Если на материальное тело действуют несколько сил, то результирующую силу можно найти из выражения:

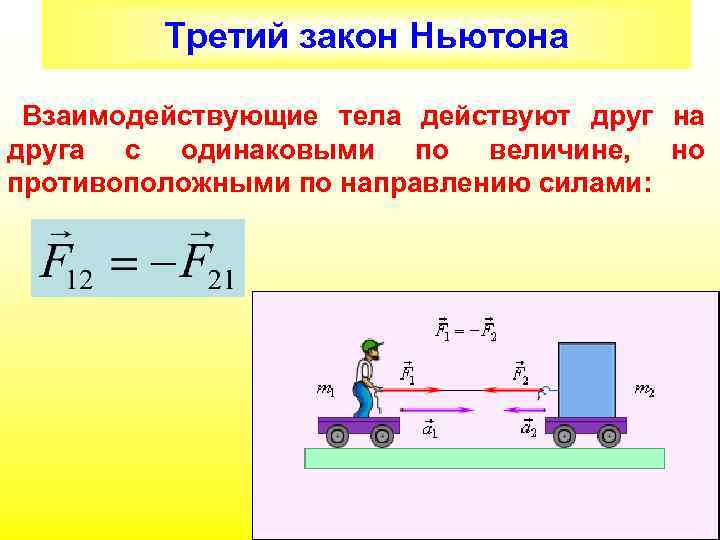Третий закон Ньютона Взаимодействующие тела действуют друг на друга с одинаковыми по величине, но противоположными по направлению силами:

Однако, третий закон справедлив не всегда. Он выполняется в случае контактных взаимодействий, т. е. при соприкосновении тел, а также при взаимодействии тел, находящихся на расстоянии друг от друга, но покоящихся друг относительно друга. Законы Ньютона плохо работают при (релятивистская механика) а также, при движении тел очень малых размеров, сравнимых с размерами элементарных частиц. Так, например, нуклоны внутри ядра, кварки внутри нуклонов, и даже электроны внутри атома, не подчиняются законам Ньютона.

5 Силы в механике 1 Сила тяготения. Сила тяжести (вес тела); 2 Силы упругости; 3 Силы трения.

5. 1 Сила тяжести и вес тела Одна из фундаментальных сил – сила гравитации проявляется на Земле в виде силы тяготения – сила, с которой все тела притягиваются к Земле. где r – расстояние между точками, G=6, 67 10 -11 Н м 2/кг 2 – гравитационная постоянная.

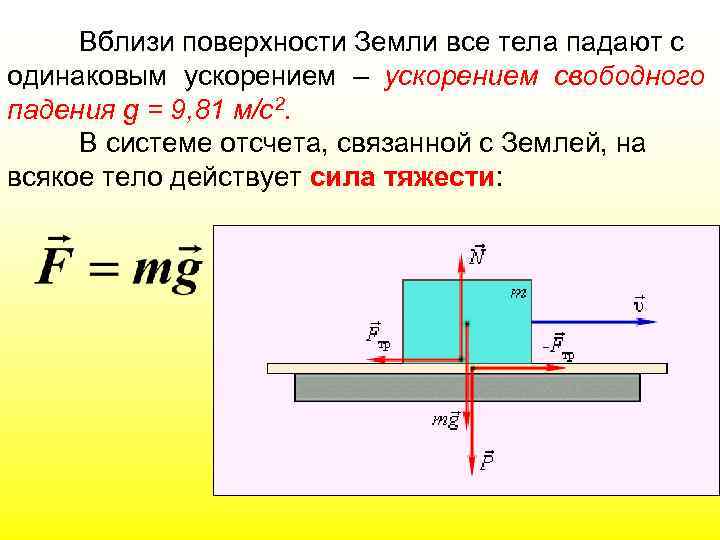Вблизи поверхности Земли все тела падают с одинаковым ускорением – ускорением свободного падения g = 9, 81 м/с2. В системе отсчета, связанной с Землей, на всякое тело действует сила тяжести:

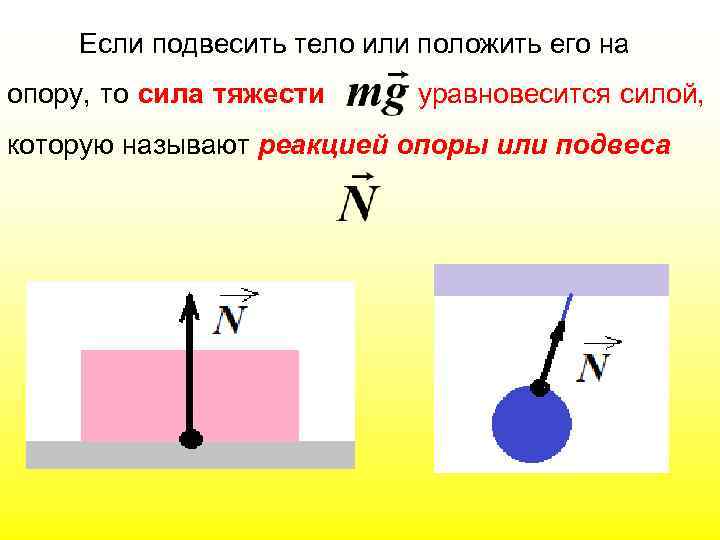Если подвесить тело или положить его на опору, то сила тяжести уравновесится силой, которую называют реакцией опоры или подвеса

По третьему закону Ньютона тело действует на подвес или опору с силой которая называется весом тела. Поскольку силы и уравновешивают друга, то выполняется соотношение Согласно третьему закону Ньютона: Значит

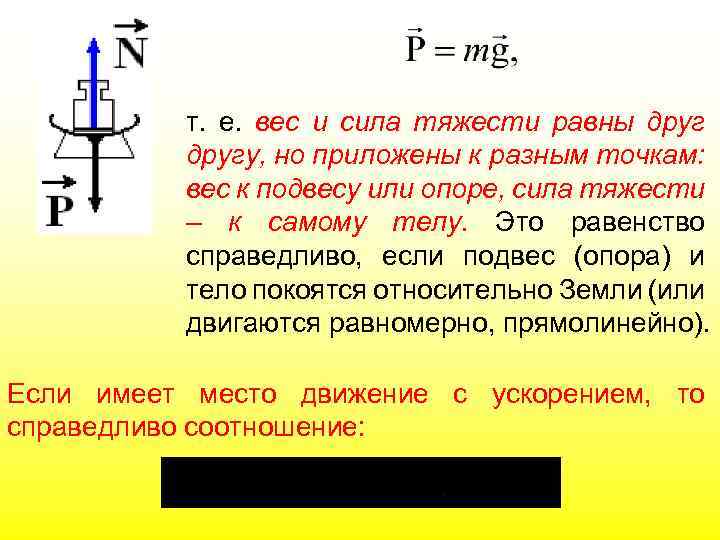т. е. вес и сила тяжести равны другу, но приложены к разным точкам: вес к подвесу или опоре, сила тяжести – к самому телу. Это равенство справедливо, если подвес (опора) и тело покоятся относительно Земли (или двигаются равномерно, прямолинейно). Если имеет место движение с ускорением, то справедливо соотношение:

Вес тела может быть больше или меньше силы тяжести: если g и a направлены в одну сторону (тело движется вниз или падает), то и если наоборот, то Если же тело движется с ускорением то – т. е. наступает состояние невесомости. Пример: космический корабль на орбите.

5. 2 Сила упругости Под действием внешних сил возникают деформации (т. е. изменение размеров и формы) тел. Если после прекращения действия внешних сил восстанавливаются прежние форма и размеры тела, то деформация называется упругой. При превышении предела упругости деформация становится пластичной или неупругой, т. е. первоначальные размеры и форма тела полностью не восстанавливается.

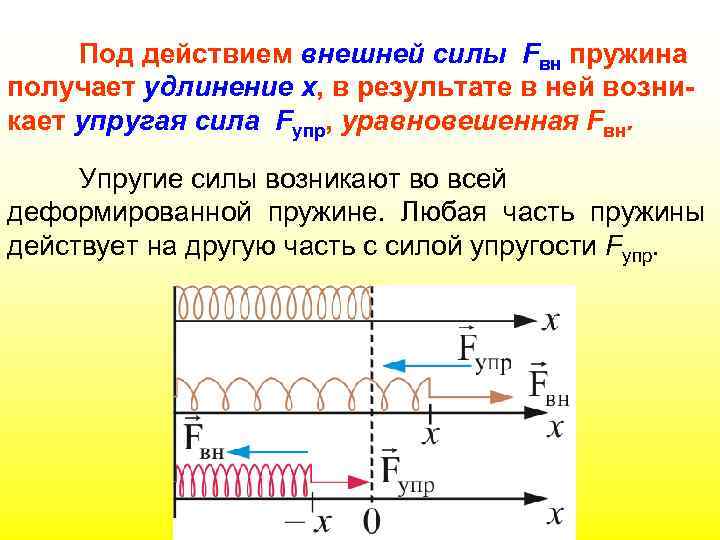Под действием внешней силы Fвн пружина получает удлинение x, в результате в ней возникает упругая сила Fупр, уравновешенная Fвн. Упругие силы возникают во всей деформированной пружине. Любая часть пружины действует на другую часть с силой упругости Fупр.

Так как упругая сила отличается от внешней только знаком, т. е. то закон Гука можно записать в виде:

5. 3 Силы трения Трение подразделяется на внешнее и внутреннее. Внешнее трение возникает при относительном перемещении двух соприкасающихся твердых тел (трение скольжения или трение покоя). Внутреннее трение наблюдается при относительном перемещении частей одного и того же сплошного тела (например, жидкость или газ).

Различают сухое и жидкое (или вязкое) трение. Жидким (вязким) называется трение между твердым телом и жидкой или газообразной средой или ее слоями. Сухое трение, в свою очередь, подразделяется на трение скольжения и трение качения.

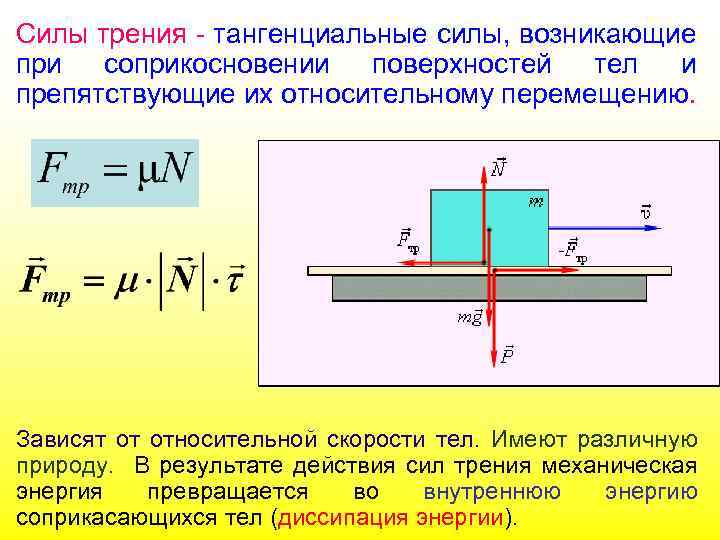Силы трения - тангенциальные силы, возникающие при соприкосновении поверхностей тел и препятствующие их относительному перемещению. Зависят от относительной скорости тел. Имеют различную природу. В результате действия сил трения механическая энергия превращается во внутреннюю энергию соприкасающихся тел (диссипация энергии).

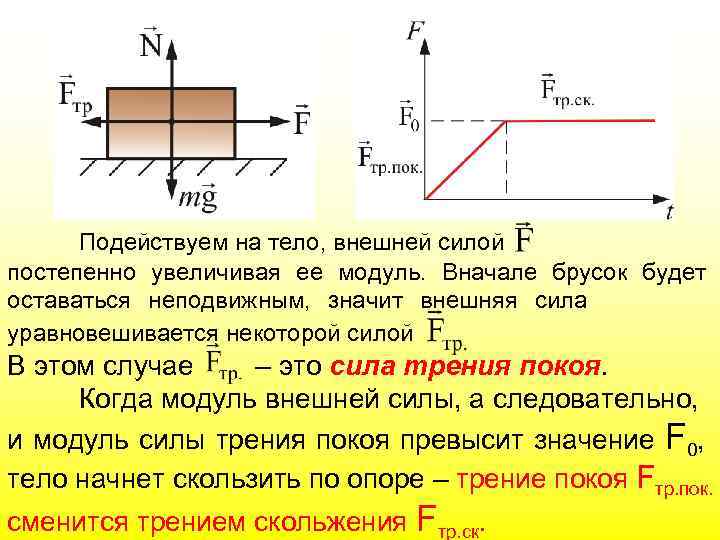Подействуем на тело, внешней силой постепенно увеличивая ее модуль. Вначале брусок будет оставаться неподвижным, значит внешняя сила уравновешивается некоторой силой В этом случае – это сила трения покоя. Когда модуль внешней силы, а следовательно, и модуль силы трения покоя превысит значение F 0, тело начнет скользить по опоре – трение покоя Fтр. пок. сменится трением скольжения Fтр. ск.

6 Динамика вращательного движения твердого тела относительно оси Обозначим Ii – момент инерции точки находящейся на расстоянии ri от оси вращения: Т. к. тело состоит из огромного количества точек и все они находятся на разных расстояниях от оси вращения, то момент инерции твердого тела равен: где r – расстояние от оси вращения до dm. Момент инерции I – величина скалярная.

Моменты инерции шара, сферы, диска, обруча и стержня: Шар Диск Сфера Обруч Стержень

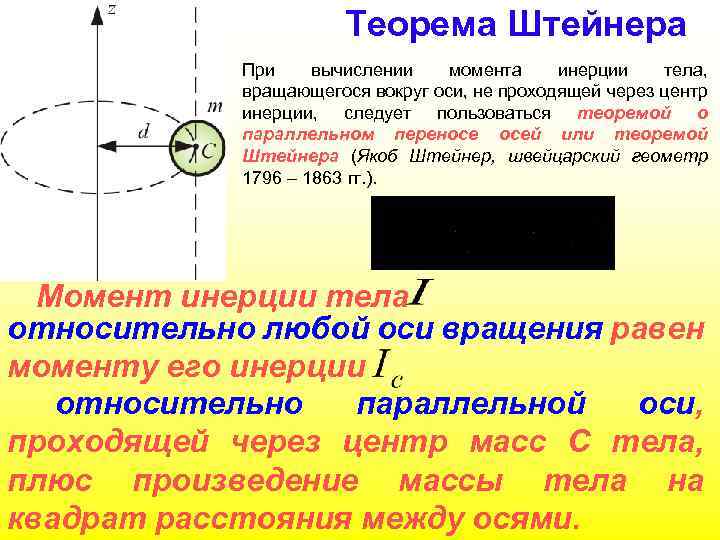Теорема Штейнера При вычислении момента инерции тела, вращающегося вокруг оси, не проходящей через центр инерции, следует пользоваться теоремой о параллельном переносе осей или теоремой Штейнера (Якоб Штейнер, швейцарский геометр 1796 – 1863 гг. ). Момент инерции тела относительно любой оси вращения равен моменту его инерции относительно параллельной оси, проходящей через центр масс С тела, плюс произведение массы тела на квадрат расстояния между осями.

Пример: стержень массой m, длиной l, вращается вокруг оси, проходящей через конец стержня.

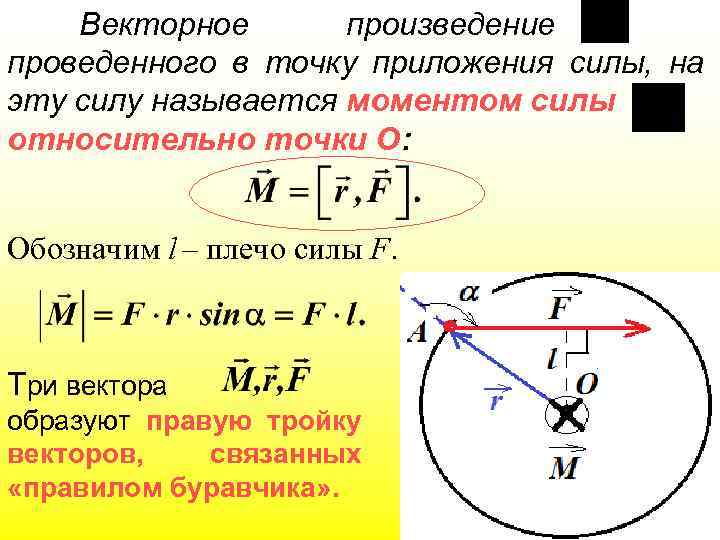Векторное произведение проведенного в точку приложения силы, на эту силу называется моментом силы относительно точки О: Обозначим l – плечо силы F. Три вектора образуют правую тройку векторов, связанных «правилом буравчика» .

величина, характеризующая вращательный эффект силы, при действии ее на твердое тело. Правило знаков: , если вызывает вращение тела против часовой стрелки, , если вызывает вращение тела по часовой стрелке.

Векторное произведение точки на её импульс называется моментом импульса этой точки относительно точки О: Три вектора образуют правую тройку векторов, связанных «правилом буравчика» .

Основной закон динамики вращательного движения Это основное уравнение динамики тела вращающегося вокруг неподвижной оси: Скорость изменения момента импульса равна моменту внешних сил , действующих на тело.