ДИСЦИПЛИНА: МАТЕМАТИКА Специальность: Экономическая безопасность Раздел 3. Математический анализ и дифференциальные уравнения Тема 9. Производная и дифференциал функции одной переменной
ЛЕКЦИЯ 9. 5. БЩЕЕ ИССЛЕДОВАНИЕ О ФУНКЦИИ Учебные вопросы 1. Монотонность функции, точки экстремума 2. Выпуклость и вогнутость графика функции, точки перегиба 3. Общая схема исследования функции
ПЕРВЫЙ УЧЕБНЫЙ ВОПРОС Монотонность функции, точки экстремума
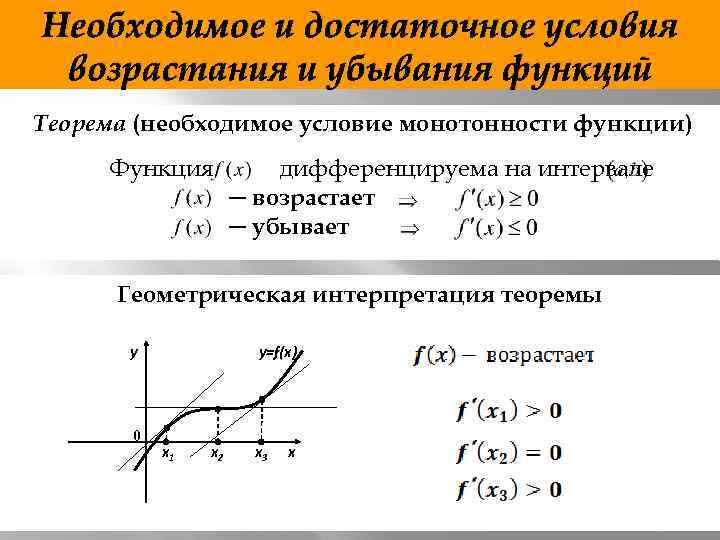
Необходимое и достаточное условия возрастания и убывания функций Теорема (необходимое условие монотонности функции) Функция дифференцируема на интервале ─ возрастает ─ убывает Геометрическая интерпретация теоремы y 0 y=f(x) x 1 x 2 x 3 x
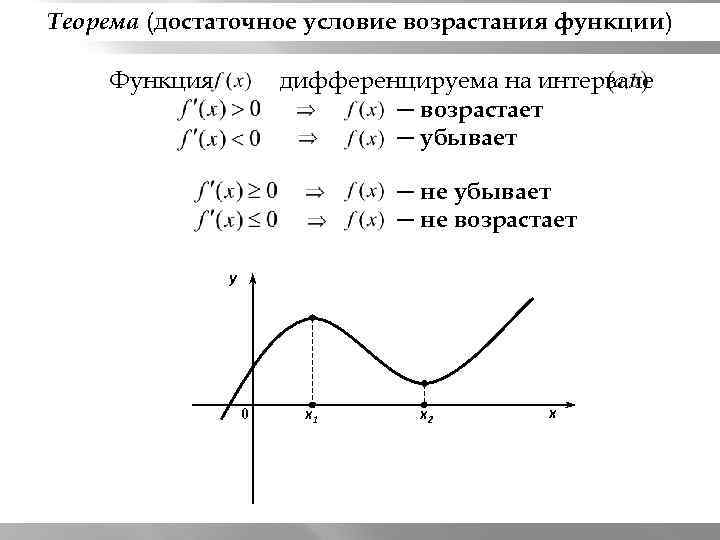
Теорема (достаточное условие возрастания функции) Функция дифференцируема на интервале ─ возрастает ─ убывает ─ не возрастает y 0 x 1 x 2 x
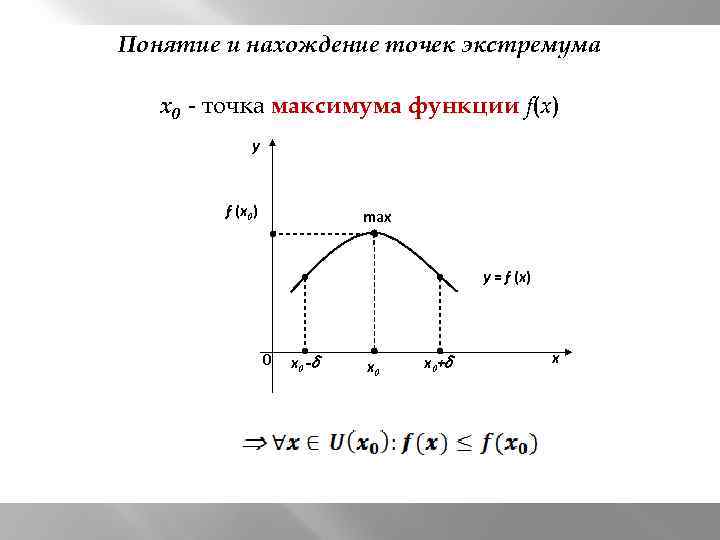
Понятие и нахождение точек экстремума x 0 - точка максимума функции f(x) y f (x 0) max y = f (x) 0 x 0 - x 0+ x
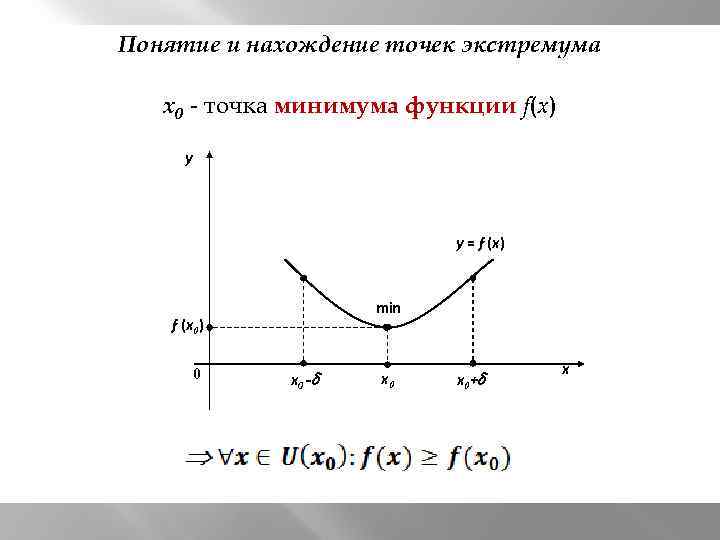
Понятие и нахождение точек экстремума x 0 - точка минимума функции f(x) y y = f (x) min f (x 0) 0 x 0 - x 0+ x
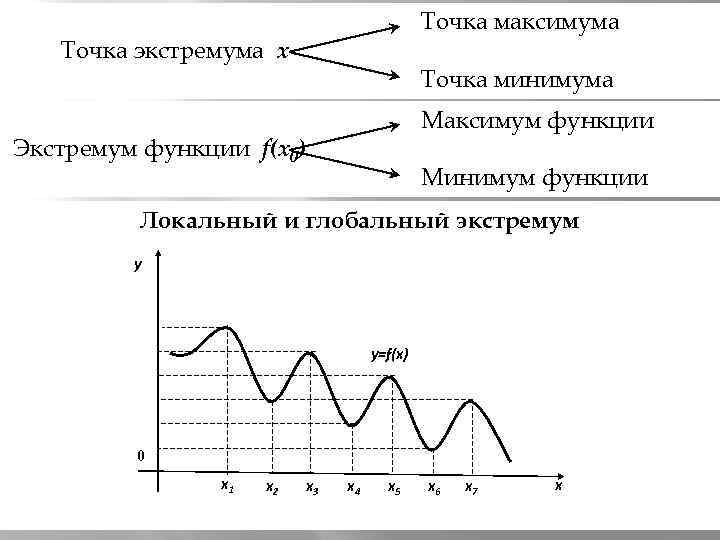
Точка максимума Точка экстремума х Точка минимума Максимум функции Экстремум функции f(х0) Минимум функции Локальный и глобальный экстремум y y=f(x) 0 x 1 x 2 x 3 x 4 x 5 x 6 x 7 x
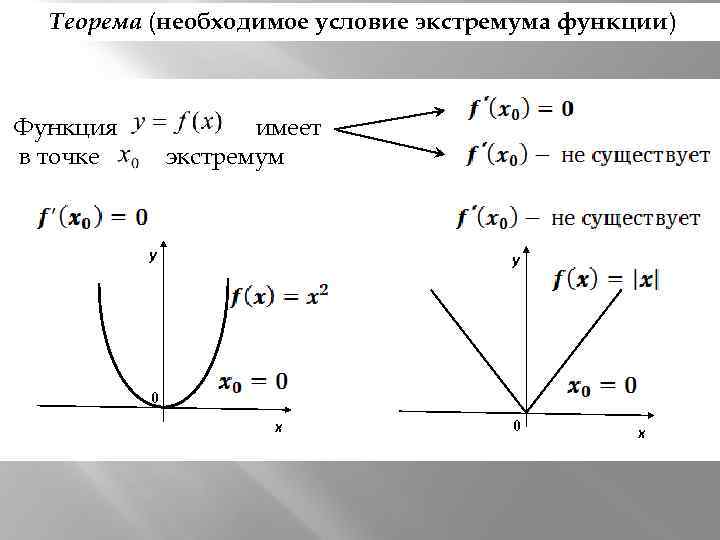
Теорема (необходимое условие экстремума функции) Функция в точке имеет экстремум y y 0 x
Пример. y Решение. х=0 – стационарная точка, 0 x х=0 не точка экстремума
Теорема (достаточное условие экстремума) Непрерывная функция дифференцируема в некоторой окрестности точки - стационарная точка + - f (x 0) x 0 +
ВТОРОЙ УЧЕБНЫЙ ВОПРОС Выпуклость и вогнутость графика функции, точки перегиба
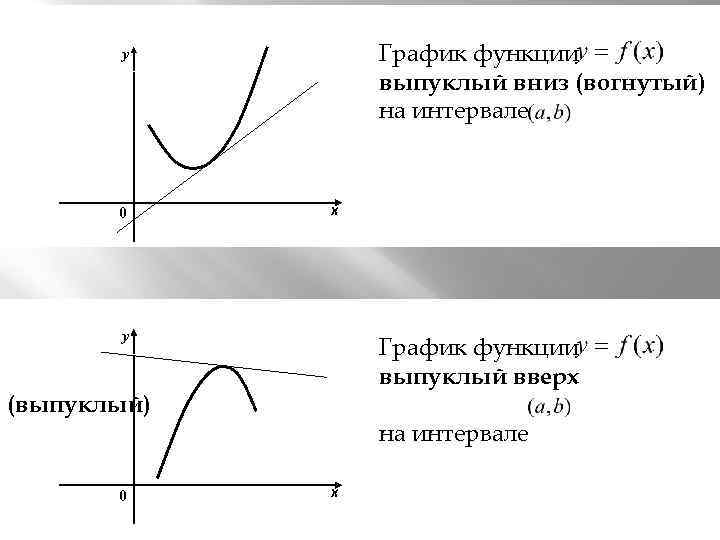
График функции выпуклый вниз (вогнутый) на интервале у 0 х у График функции выпуклый вверх (выпуклый) 0 на интервале х
Теорема (достаточное условие выпуклости) - дважды дифференцируема на , следовательно, - выпукла вниз - выпукла вверх Теорема (необходимое условие выпуклости) - дважды дифференцируема на - выпукла вниз , следовательно, - выпукла вверх , следовательно,
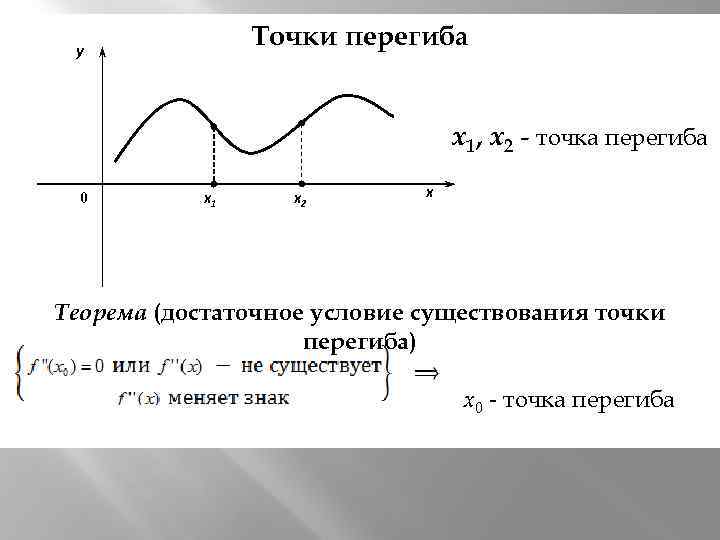
х0 Точки перегиба y х1, х2 - точка перегиба 0 x 1 x 2 x Теорема (достаточное условие существования точки перегиба) х0 - точка перегиба
ТРЕТИЙ УЧЕБНЫЙ ВОПРОС Общая схема исследования функций
Общая схема 1. Определить область определения функции. 2. Найти вертикальные асимптоты. 3. Найти горизонтальные и наклонные асимптоты и исследовать функцию на бесконечности. 4. Определить точки пересечения графика функции с осями координат Oх и Oу. 5. Указать, если они имеются, основные свойства функции: четность, нечетность, периодичность функции. 6. Найти точки экстремума и сам экстремум функции, интервалы возрастания и убывания функции. 7. Найти точки перегиба и интервалы выпуклости графика функции. 8. Найти значения функции в некоторых дополнительных точках, если это необходимо.
Контрольные вопросы 1. Необходимое и достаточное условия монотонности функции. 2. Понятие и нахождение точек экстремума. 3. Выпуклость и вогнутость графика функции, точки перегиба, их нахождение. 4. Понятие и виды асимптот графика функции, их нахождение. 5. Общая схема исследования функции.
Спасибо за внимание Презентацию составила профессор кафедры математики и информатики Большакова Л. В.
Скачать презентацию ДИСЦИПЛИНА МАТЕМАТИКА Специальность Экономическая безопасность Раздел 3 Математический
Пр_Лекция_9.5_М_ЭБ.pptx