ДИСЦИПЛИНА МАТЕМАТИЧЕСКИЙ АНАЛИЗ Преподаватель к п н

ДИСЦИПЛИНА: МАТЕМАТИЧЕСКИЙ АНАЛИЗ Преподаватель: к. п. н. , доцент Юлия Александровна Семеняченко

Рекомендуемая литература: Мордкович, А. Г. Математический анализ: Учебное пособие / А. Г. Мордкович, А. С. Солодовников. – М. : Вербум М, 2000. – 416 с. Шипачев, В. С. Высшая математика: Учеб. Для студентов вузов / В. С. Шипачев. – М. : Высшая школа, 2005. – 479 с. Баврин, И. И. Высшая математика: Учебник для студентов высших педагогических учебных заведений / И. И. Баврин. – М. : Академия, 2008. – 611 с. Высшая математика для экономистов : учебник для студентов вузов, обучающих ся по экон. спец. / под ред. Н. Ш. Кремера. М. : ЮНИТИ: UNITY, 2007. – 478 с. Шипачев, В. С. Задачи по высшей математике: Учеб. пособие для вузов / В. С. Шипачев. – М. : Высш. шк. , 1997. – 304 с. Берман, Г. Н. Сборник задач по курсу математического анализа : учеб. Пособие / Г. Н. Берман. – СПб. : Профессия, 2006. – 432 с. Высшая математика для экономистов: практикум / под ред. Н. Ш. Кремера. М. : ЮНИТИ: UNITY, 2007. – 477 с. Мордкович, А. Г. Задачник по введению в математический анализ / А. Г. Мордкович, М. В. Шуркова. – М. : Мнемозина, 2008. – 136 с. Кудрявцев Л. Д. Сборник задач по математическому анализу: Функции нескольких переменных. СПб. 1994. Семеняченко, Ю. А. Математический анализ. Введение в анализ: Пособие для самостоятельной работы студентов педагогических вузов / Ю. А. Семеняченко. – М. : МГПУ, 2005. – 75 с.

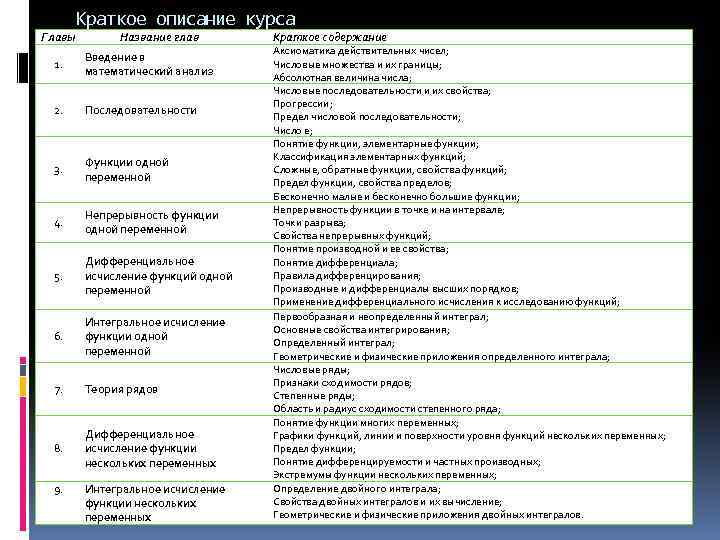Краткое описание курса Главы Название глав 1. Введение в математический анализ 2. Последовательности 3. Функции одной переменной 4. Непрерывность функции одной переменной 5. Дифференциальное исчисление функций одной переменной 6. Интегральное исчисление функции одной переменной 7. Теория рядов 8. Дифференциальное исчисление функции нескольких переменных 9. Интегральное исчисление функции нескольких переменных Краткое содержание Аксиоматика действительных чисел; Числовые множества и их границы; Абсолютная величина числа; Числовые последовательности и их свойства; Прогрессии; Предел числовой последовательности; Число е; Понятие функции, элементарные функции; Классификация элементарных функций; Сложные, обратные функции, свойства функций; Предел функции, свойства пределов; Бесконечно малые и бесконечно большие функции; Непрерывность функции в точке и на интервале; Точки разрыва; Свойства непрерывных функций; Понятие производной и ее свойства; Понятие дифференциала; Правила дифференцирования; Производные и дифференциалы высших порядков; Применение дифференциального исчисления к исследованию функций; Первообразная и неопределенный интеграл; Основные свойства интегрирования; Определенный интеграл; Геометрические и физические приложения определенного интеграла; Числовые ряды; Признаки сходимости рядов; Степенные ряды; Область и радиус сходимости степенного ряда; Понятие функции многих переменных; Графики функций, линии и поверхности уровня функций нескольких переменных; Предел функции; Понятие дифференцируемости и частных производных; Экстремумы функции нескольких переменных; Определение двойного интеграла; Свойства двойных интегралов и их вычисление; Геометрические и физические приложения двойных интегралов.

Глава 1. Введение в математический анализ § 1. Аксиоматика множеств рациональных и действительных чисел П. 1. Аксиомы множества рациональных чисел ОПР. 1. 1. Рациональным называется число, которое можно представить в виде дроби , где целое число, а натуральное число. Всякое рациональное число является либо целым, либо может быть представлено в виде конечной или периодической бесконечной десятичной дроби.

Аксиомы сложения Для каждой пары чисел a и b существует единственное число называемое его суммой, для которой справедливы следующие свойства: 1) (переместительное свойство); 2) (сочетательное свойство); 3) Существует нулевой элемент, обозначаемый « » , для которого справедливо ; 4) Для каждого числа существует симметричное ему число , для которого .

Аксиомы умножения Для каждой пары чисел a и b существует единственное число , называемое его произведением, для которого справедливы следующие свойства: 1) (переместительное свойство умножения); 2) (сочетательное свойство умножения); 3) Существует единичный элемент, обозначаемый « » , для которого ; 4) Для каждого числа , отличного от нуля, существует обратный элемент или , для которого . Распределительное свойство:

Аксиомы порядка Для каждой пары чисел a и b существует единственное отношение: либо , либо . 1) Из того, что и , следует, что (транзитивное свойство); 2) Если , то ; 3) Если , то .

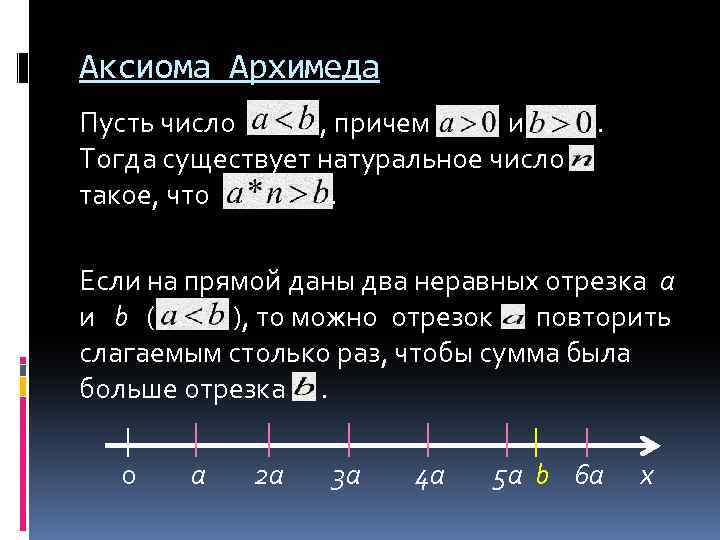Аксиома Архимеда Пусть число , причем и . Тогда существует натуральное число такое, что . Если на прямой даны два неравных отрезка a и b ( ), то можно отрезок повторить слагаемым столько раз, чтобы сумма была больше отрезка . 0 a 2 a 3 a 4 a 5 a b 6 a x

Геометрическое изображение рациональных чисел а О М