Дисциплина Математические модели в

Дисциплина Математические модели в экономике Тема 1. Построение экономико-математических моделей n Алгоритм построения модели Определить искомые величины задачи Определить цель решения задачи Значение параметра задачи = оптимальному решению К чему должно стремиться оптимальное решение – max, min? Какие условия в отношении искомых величин и ресурсов задачи должны быть выполнены? Запись математической модели

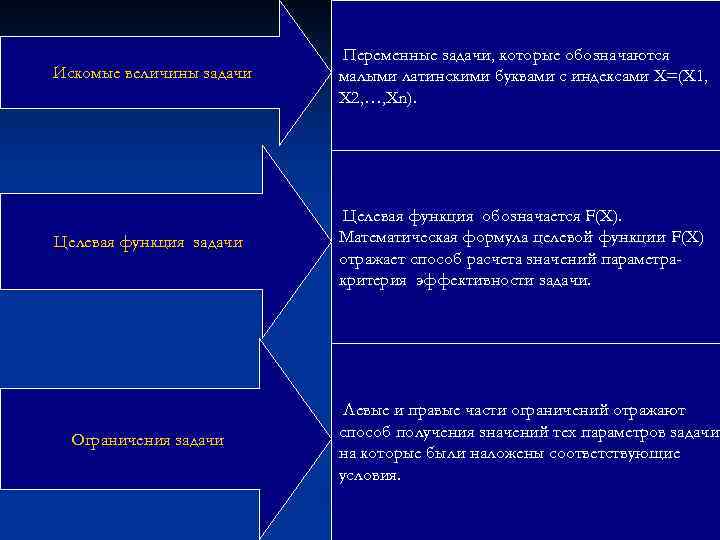
Переменные задачи, которые обозначаются Искомые величины задачи малыми латинскими буквами с индексами Х=(Х 1, Х 2, …, Хn). Целевая функция обозначается F(Х). Целевая функция задачи Математическая формула целевой функции F(X) отражает способ расчета значений параметра- критерия эффективности задачи. Левые и правые части ограничений отражают Ограничения задачи способ получения значений тех параметров задачи, на которые были наложены соответствующие условия.

Пример построения экономико-математической модели Условие задачи: Коммерческому отделу поручили проанализировать совместную деятельность подразделений фабрики по изготовлению и продаже двух видов краски для внутренних наружных работ. Краска поступает в продажу по цене 3000 руб. и 2000 руб. за 1 т. Для производства красок используют два вида сырья: А и В, максимально возможные суточные запасы которых составляют 3 и 4 т соответственно. Расход сырья на производство 1 т красок приведен в таблице. Изучение конъюнктуры спроса на рынке сбыта показало, что суточный спрос на краску для внутренних работ никогда не превышал спроса на краску для наружных работ более чем на 1, 5 т, а спрос на краску для внутренних работ не превышал 2 т в сутки. Какое количество краски каждого вида необходимо производить фабрике, чтобы доход от ее реализации был максимальным? Цена 1 т краски: для внутренних работ – 3000 руб. , для наружных – 2000 руб. Сырье Расход сырья на 1 Запас сырья, т т краски для наружных работ, внутренних работ, т А 0, 5 1 3 В 1 0, 5 4

Решение задачи 1. Переменные задачи. В задаче следует установить, сколько краски каждого вида надо производить, поэтому искомыми величинами, а значит, и переменными задачи являются суточные объемы производства каждого вида красок: Х 1 – суточный объем производства краски для наружных работ (т краски/сутки); Х 2 – суточный объем краски для внутренних работ (т краски/сутки); 2. Целевая функция. Цель задачи – максимальный доход от реализации продукции. F(X)=3 Х 1+2 Х 2 max (тыс. руб. /сутки) (тыс. руб. /т. краски* т. краски/сутки = тыс. руб. /сутки)

3. Ограничения. Возможные объемы производства красок Х 1 и Х 2 ограничиваются следующими условиями: - Количество сырья А и В, израсходованного в течение суток на производство красок обоих видов, не может превышать суточного запаса этих ингредиентов на складе; - Согласно результатам изучения рыночного спроса суточный объем производства краски для внутренних работ может превышать объем производства для наружных работ не более чем на 1, 5 т краски, а спрос на краску для внутренних работ никогда не превышал 2 т краски в сутки; - Объем производства красок не может быть выражен отрицательными значениями. Отсюда вывод по группам ограничений задачи: 1. Расход сырья; 2. Рыночный спрос на краску; 3. Неотрицательный объем производства.

Математическая модель задачи имеет следующий вид: F(Х)=3 Х 1+2 Х 2 max 0, 5 X 1+X 2<=3 X 1+0, 5 X 2<=4 X 2 -X 1<=1, 5 X 2<=2; X 1>=0; X 2>=0; Вывод: найти такой план производства продукции X=(X 1, X 2), удовлетворяющий системе ограничений, при котором целевая функция принимает максимальное значение.

Решение задачи графическим методом: 1. В системе координатной плоскости строят прямые 0, 5 X 1+X 2=3 X 1+0, 5 X 2=4 X 2 -X 1=1, 5 X 2=2; 2. Неравенства X 1>=0; X 2>=0; означают, что область допустимых решений задачи будет расположена в первой координатной четверти. 3. Находим полуплоскости, определенные каждым из ограничений задачи. Затем находим их пересечение, что будет являться ОДР (областью допустимых решений) задачи.

4. Строим вектор N=(3, 2). Где направление вектора будет определено коэффициентами целевой функции. 5. Перпендикулярно вектору N строим линию уровня (опорную линию). 6. Линию уровня перемещаем вдоль вектора N для нахождения наибольшего значения до самой удаленной точки ОДР. 7. Определяем координаты этой точки и определяем, на пересечении каких линий она находится. Строим систему уравнений этих линий и определяем оптимальный план. 8. Подставляя полученный результат в целевую функцию получаем значение целевой функции.

Для чего проводится анализ функции на чувствительность. Некоторые параметры задачи линейного программирования (финансы, запасы сырья, производственные мощности) можно регулировать. Эта информация получается в результате анализа функции на чувствительность. Если обнаруживается, что оптимальное решение можно значительно улучшить за счет небольших изменений заданных параметров, то целесообразно реализовать эти изменения.

При анализе устойчивости необходимо дать ответы на следующие вопросы: 1) На сколько могут быть увеличены запасы недефицитных ресурсов для улучшения оптимального решения при сохранении общей структуры решения? 2) На сколько могут быть снижены запасы дефицитных ресурсов при сохранении общей структуры оптимального решения? 3) Какие дефицитные ресурсы следует увеличивать в первую очередь?

4)На сколько могут быть снижены запасы недефицитных ресурсов при сохранении оптимальности полученного результата? 5) Каковы пределы изменения коэффициентов целевой функции, при которых не происходит изменения оптимального решения? 6) На сколько следует изменить тот или иной коэффициент целевой функции, чтобы сделать дефицитный ресурс недефицитным и наоборот?