Direct Variation What is it and how do

Direct Variation: What is it and how do I know when I see it? Do Now: Find the slope of the line that contains the points (-3, 5) and (6, -1).

Vocabulary p The terms DIRECT VARIATION and DIRECT PROPORTION will be used interchangeably. They mean the same thing. p The terms CONSTANT OF PROPORTIONALITY and CONSTANT OF VARIATION will be used interchangeably. They mean the same thing.

What is a Direct Variation or a Direct Proportion? p When one value increases, the other value also increases OR p When one value decreases, the other value also decreases p When one quantity always changes by the same factor (the constant of proportionality), the two quantities are directly proportional.

Real World Examples of Direct Variation Situations… The more time I drive (at a constant rate), the more miles I go. p If I increase a recipe for more people, the more of an ingredient I need. p The more hours I work, the more money I make. p The more CD’s I purchase, the more money it costs. p The less cheese I buy at the deli, the less money I pay. p The less water you drink, the less trips to the bathroom you have to make. p

Now you come up with a few examples of your own… p Raise your hand if you have an example of when both values would increase p Raise your hand if you have an example of when both values would decrease p Choose one of each to write in your notes

How do we know if we have a direct variation? p We can look at three different aspects of the situation: 1. GRAPHS 2. TABLES 3. EQUATIONS

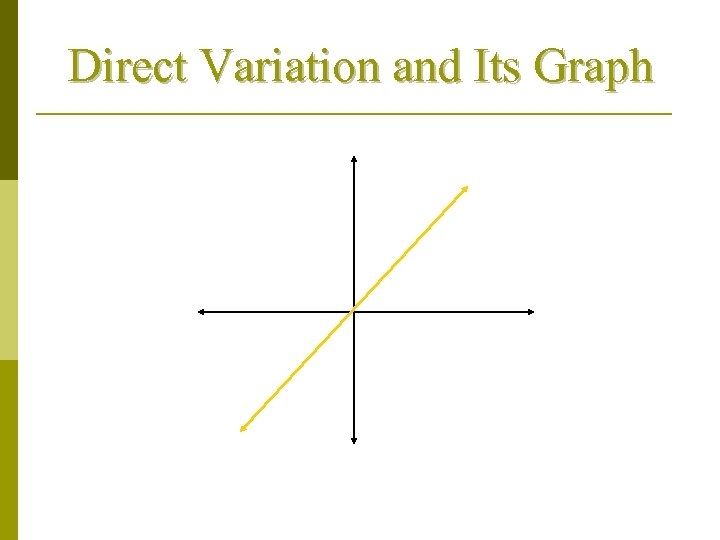Direct Variation and Its Graph

Characteristics of Direct Proportion Graph… The graph will always go through the ORIGIN (point 0, 0) on the coordinate plane…this means when x=0, y=0 on the graph p The graph will always be in Quadrant I (all positive numbers) and Quadrant III (all negative numbers) p The graph will always be a straight line p As the “x” value increases, the “y” value always increases p These things will always occur in DIRECT VARIATIONS…if it doesn’t then it is NOT a DIRECT PROPORTION!

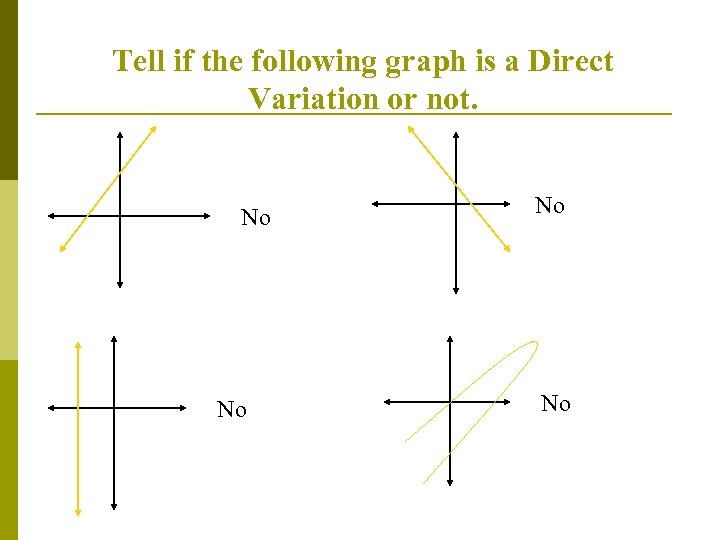Tell if the following graph is a Direct Variation or not. No No

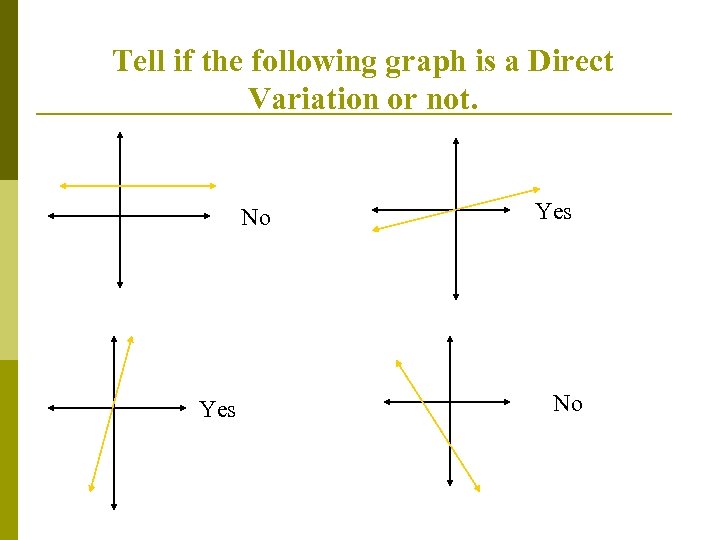Tell if the following graph is a Direct Variation or not. No Yes No

Independent VS. Dependent p The x-axis is the independent variable; this means it does NOT depend on the y value p The y-axis is the dependent variable; this means it DOES depend on the x variable for its value.

Example… p You went on a hiking trip, and you graphed your distances at various times throughout your trip. As the time you hiked increased, the distance traveled also increased. The distance depends on the time; therefore, the distance is the dependent variable and it is graphed on the y-axis (vertical). The time is independent (time still goes on whether or not the distance changes), so it is graphed on the x-axis (horizontal).

Direct Variation Equations: • Y varies directly as x means that y = kx where k is the constant of variation. • Another way of writing this is k = • X is the independent variable • Y is the dependent variable • K is the constant of proportionality

Examples of Direct Variation Equations (y = kx or y/x = k)… y y y = = = 4 x x 2 x 2. 5 x ⅝x 0. 75 x k k k = = = 4 1 2 2. 5 ⅝ 0. 75

Are these examples of direct variation? If so, find the constant of variation. p

Direct Variation & Tables of Values You can make a table of values for “x” and “y” and see how the values behave. You could have a direct variation if… p As “x” increases in value, “y” also increases in value OR p As “x” decreases in value, “y” also decreases in value

Examples of Direct Variation: Note: As “x” increases, 6, 7, 8 “y” also increases. 12, 14, 16 What is the constant of variation of the table above? Start with the direct variation equation: y = kx Pick one pair of x and y values and substitute into the equation 12 = k · 6 (this is a one-step equation, so solve for k) 12/6 = k → k=2 Now you can write the equation for this direct variation: y = 2 x

Examples of Direct Variation: Note: X decreases, 30, 15, 9 And Y decreases. 10, 5, 3 What is the constant of variation of the table above? Start with the direct variation equation: y = kx Pick one pair of x and y values and substitute into the equation 10 = k · 30 (this is a one-step equation, so solve for k) 10/30 = k → (simplify 10/30) → k = ⅓ Now you can write the equation for this direct variation: y = ⅓ · x

Is this a direct variation? If yes, give the constant of variation (k) and the equation. Yes! y = kx • Pick an x & y pair and substitute into the direct variation equation to solve for k. • Remember the constant must hold true for every (x, y) pair 6=k· 4 k = 6/4 = 3/2 = 1 ½ Therefore the equation for this table is: y = 1 ½ · x

Is this a direct variation? If yes, give the constant of variation (k) and the equation. Yes! y = kx * Pick an x & y pair and substitute into the direct variation equation & find k. 25 = k · 10 25/10 = k 5/2 or 2 ½ = k * Remember the constant must hold true for every x, y pair. Therefore the equation for this table is: y=2½·x

Is this a direct variation? If yes, give the constant of variation (k) and the equation. No! If you look at the values in the table, you should notice as “x” decreases, “y” increases, so you know you CANNOT have a direct variation! Also, there is no constant of proportionality. There is not one number you multiply by x to get y for each pair in the table.

Which is the equation that describes the following table of values? 1. 2. 3. 4. y = -2 x y = ½ x xy = 200 Answer Now

Using Direct Variation to find unknowns (y = kx) Given y varies directly with x, and y = 28 when x=7, Find x when y = 52. HOW? ? ? 2 step process 1. Find the constant of variation y = kx → 28 = k · 7 (divide both sides by 7) k=4 2. Use y = kx. Find the unknown (x). 52= 4 x or 52/4 = x x= 13 Therefore: X =13 when Y=52

Using Direct Variation to find unknowns (y = kx) Given that y varies directly with x, and y = 3 when x=9, Find y when x = 40. 5. HOW? ? ? 2 step process 1. Find the constant of variation. Y = kx → 3=k· 9 (divide both sides by 9) k = 3/9 = 1/3 2. Use y = kx. Find the unknown (x). y= (1/3)40. 5 y= 13. 5 Therefore: X =40. 5 when Y=13. 5

Using Direct Variation to solve word problems Problem: Step One: Find points in table A car uses 8 gallons of gasoline to travel 290 miles. How much gasoline will the car use to travel 400 miles? Step Two: Find the constant of variation and equation: y = kx → 290 = k · 8 290/8 = k y = 36. 25 x Step Three: Use the equation to find the unknown. 400 =36. 25 x 36. 25 or x = 11. 03

Using Direct Variation to solve word problems Problem: Step One: Find points in table. Julio wages vary directly as the number of hours that he works. If his wages for 5 hours are $29. 75, how much will they be for 30 hours Step Two: Find the constant of variation. y = kx → 29. 75 = k · 5 k = 5. 95 Step Three: Use the equation to find the unknown. y = kx y = 5. 95 · 30 y = 178. 50

Direct Variation/Direct Proportion Reminder… p When you have word problems, you can also set up proportions to solve for the given situation if you prefer. p If you’re going to set up a proportion, it’s best to put the yvalue (the dependent value) over the x-value (the independent value) because then it’s already set up to solve for “k” the constant of proportionality.