Direct Proportion T A B 100 o o

Direct Proportion. T A B 100 o o O L D E 0 3 6 24 10 20 5 cm

Direct Proportion All Around. Number of Mars bars. M The number of mars bars you buy and the price you pay. ar s Direct proportion applies to all of the situations below: Cost of bars. The number of hours you work and the pay you earn. Hours you work. Pay The number of dollars you get for your pounds on holiday. Dollars. Pounds. ©Microsoft Word clipart The area of a sector of a circle and the angle at the centre. Area of sector. Angle of sector. In each of these examples two quantities are mentioned. Can you identify them in each example.

The Finding One Method. Example 1. If it costs 85 p for 5 Mars bars, what is the cost of 3 Mars bars ? Solution. Cost of 1 mars bar : Find the cost of 1 Mars bar. 85 5 = 17 p Cost of 3 Mars bars. 17 x 3 = 51 p 3 Mars bars cost 51 p. Find the cost of 3 Mars bars.

Example 2. If you are paid £ 261 for 18 hours work, how much will you be paid for 23 hours work ? Solution. I hours pay Find the pay for 1 hour. 261 18 = £ 14. 50 14. 5 x 23 = 333. 5 Calculate 23 hours pay. You are paid £ 333. 50 for 23 hours work.

Example 3. It takes a production line 90 hours to make 120 cars. How long does it take to make 330 cars ? Solution. Time for 1 car. Calculate the time to make 1 car. 90 120 = 0. 75 hours. Note : 0. 75 hours = 45 minutes. 0. 75 x 330 = 247. 5 hours Calculate the time to make 330 cars. It takes 247 hours and 30 minutes to make 330 cars.

What Goes In The Box ? Calculate the following: (1) It costs £ 21. 06 for a hotel to buy 27 boxes of cereal. How much will 35 boxes cost at the same price per box ? £ 27. 30 (2) 35 cars are produced in 87. 5 hors by a car factory. How long will it take to produce 142 cars at the same rate of working ? 355 hours (3) If you earn £ 139. 20 for 16 hours of work, what will you earn for 9 hours work paid at the same rate ? £ 78. 30

The Cross-Multiplication Method. This method is a more sophisticated way of solving direct proportion questions but it has two advantages: • It establishes a very strong routine to solve the problems. • It makes Inverse Proportion questions easier to handle. Think back to the Mars Bar problem and answer the following questions: If you have twice as many Mars Bars what happens to the price ? The price doubles. If you have three times as many Mars Bars what happens to the price? The price trebles. What about ten times the number of Mars Bars? Ten times the price.

Key Point. Whenever you have two quantities and when one is doubled or trebled etc the other quantity doubles or trebles etc , then you have direct proportion. The problem can then be solved by the method demonstrated in the following slides.

Example 1. If you are paid £ 190. 21 for 23 hours work, then what is your pay for 17 hours work ? Solution. Pay 190. 21 P Hours 23 17 23 x p = 17 x 190. 21 Identify the two quantities being talked about: Identify the two amounts that go together. Determine what is being asked for and what other info’ you have. Ask yourself “ If the first quantity is doubled , trebled etc, what happens to the second quantity ? Use arrows. . It doubles , trebles etc also. p = £ 140. 59 for 17 hours. Cross multiply to solve.

Example 2. If 5 hectares of wheat take 12 hours to harvest, how long will 27 hectares take ? Hectares Time 5 12 27 T 5 12 27 = ©Microsoft Word clipart T 5 X T = 12 x 27 T= 5 T = 64. 8 hours = 6 hr 48 min Identify the two quantities being talked about: Identify the two amounts that go together. Determine what is being asked for and what other info’ you have. Ask yourself “ If the first quantity is doubled , trebled etc, what happens to the second quantity ? Use arrows. . It doubles , trebles etc also. Cross multiply to solve.

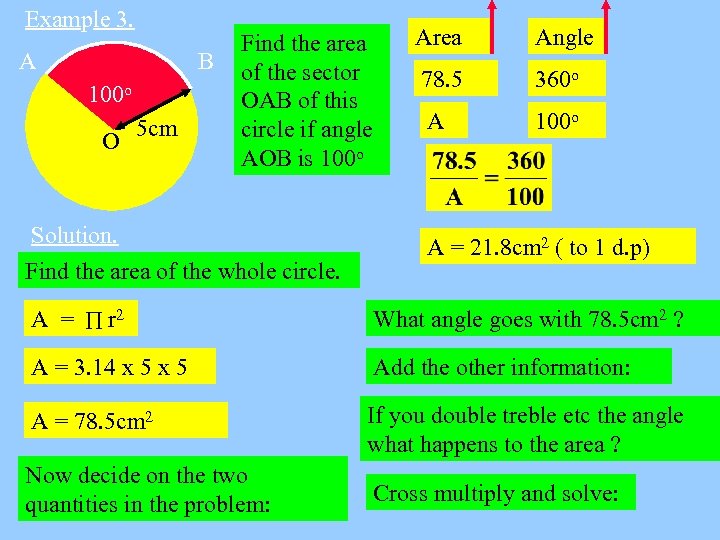
Example 3. A B 100 o O 5 cm Find the area of the sector OAB of this circle if angle AOB is 100 o Solution. Find the area of the whole circle. Area Angle 78. 5 360 o A 100 o A = 21. 8 cm 2 ( to 1 d. p) A = r 2 What angle goes with 78. 5 cm 2 ? A = 3. 14 x 5 Add the other information: A = 78. 5 cm 2 If you double treble etc the angle what happens to the area ? Now decide on the two quantities in the problem: Cross multiply and solve:

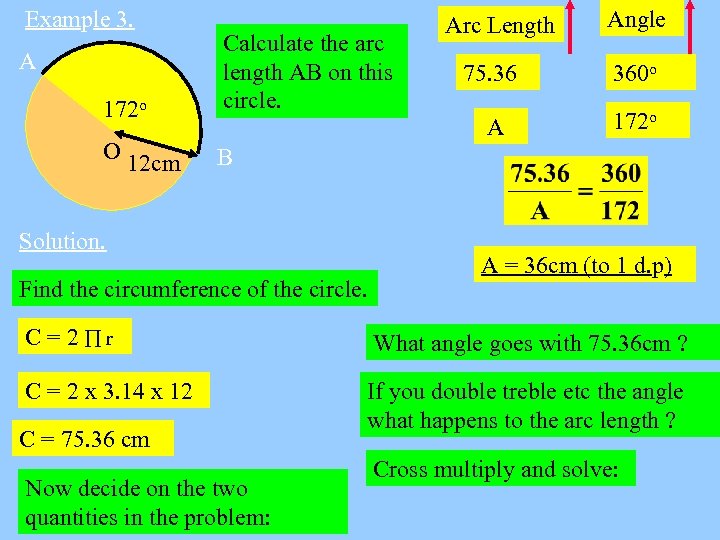
Example 3. 172 o Calculate the arc length AB on this circle. O 12 cm Arc Length Angle B A Solution. Find the circumference of the circle. 75. 36 360 o A 172 o A = 36 cm (to 1 d. p) C=2 r What angle goes with 75. 36 cm ? C = 2 x 3. 14 x 12 If you double treble etc the angle what happens to the arc length ? C = 75. 36 cm Now decide on the two quantities in the problem: Cross multiply and solve:

What Goes In The Box ? 2 (1) The shadow of a tree 7. 4 m high is 10. 6 m. How long will the shadow of a tree 8. 9 m high be at the same time ? 12. 7 m (2) Calculate the area of the sector AOB. 461. 4 cm 2 to 1 d. p A B 100 o O 23 cm (3) Calculate the arc length AB. 40. 1 cm to 1 d. p (4) You get 14 out of 23 in a test. What would you get out of 100 for the same test score ? 60. 9% to 1 d. p

Graphs Of Direct Proportion. Consider the following Direct Proportion situation : It takes 2 hours for a company to manufacture each ladder that it makes: Complete the table below: Ladders Hours 0 0 1 2 2 4 Now draw a graph of the above table: 3 6 4 8 5 10 ©Microsoft Word clipart

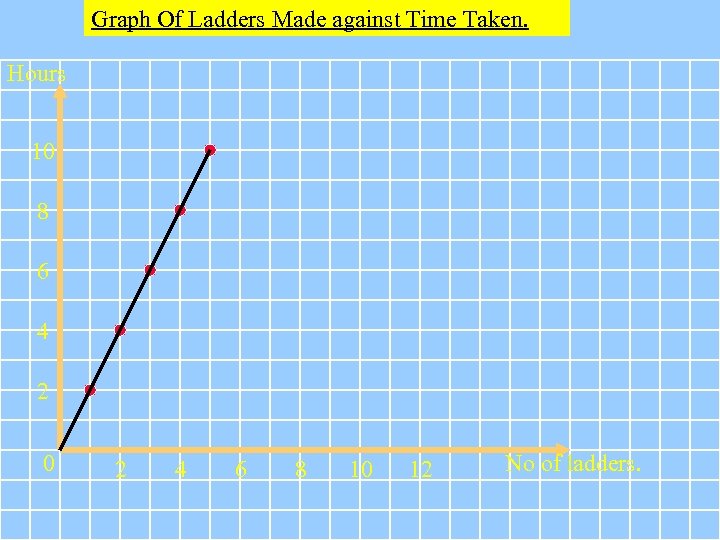
Graph Of Ladders Made against Time Taken. Hours 10 8 6 4 2 0 2 4 6 8 10 12 No of ladders.

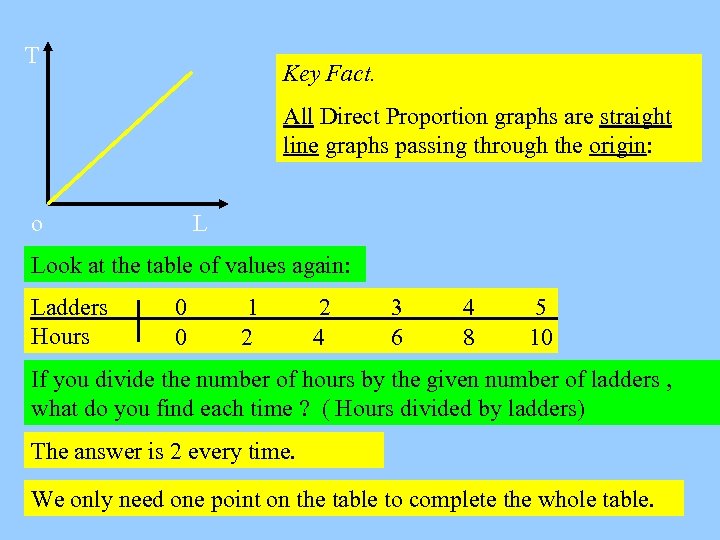
T Key Fact. All Direct Proportion graphs are straight line graphs passing through the origin: o L Look at the table of values again: Ladders Hours 0 0 1 2 2 4 3 6 4 8 5 10 If you divide the number of hours by the given number of ladders , what do you find each time ? ( Hours divided by ladders) The answer is 2 every time. We only need one point on the table to complete the whole table.

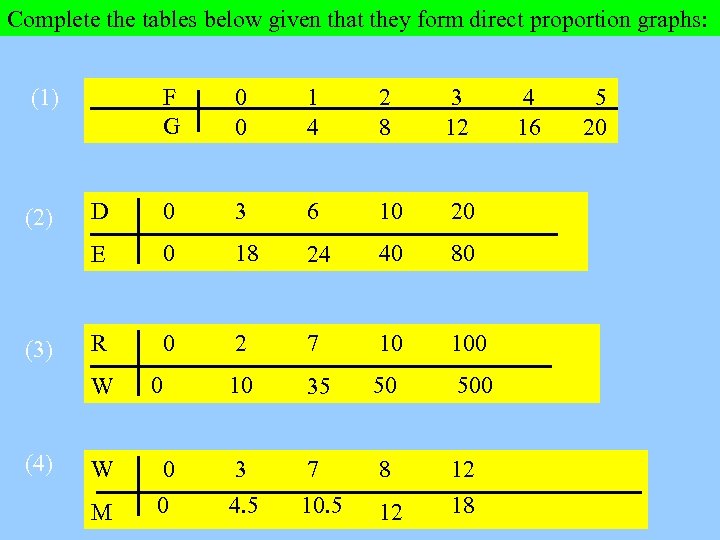
Complete the tables below given that they form direct proportion graphs: F G 0 0 1 4 2 8 3 12 D 0 3 6 10 20 E 0 18 24 40 80 R 0 2 7 10 100 (1) (2) (3) W (4) 0 10 35 50 500 W 0 0 3 4. 5 7 10. 5 8 12 18 M 12 4 16 5 20

What Goes In The Box ? 3 Complete the tables below for direct proportion and draw the graph. G 0 1 2 3 4 5 H 0 6 12 18 24 30 1 2 H 30 20 10 0 3 4 5 G