Direct Proportion Lesson Aims To understand what

Direct Proportion

Lesson Aims To understand what is meant by direct proportion.

Keywords Proportionality Direct proportion Constant of proportionality

An Example of Direct Proportion If I were to go shopping in Poundland buy 5 items, the cost would be £ 5. How much would it cost for 10 items? £ 10 …. and so on

So what can we say about the relationship between the price & number of items bought? The more items that are bought the more it costs. (No. of items bought = price paid). Therefore, the price and number of items are said to be directly proportional.

Upmarket shopping! This time we go shopping in Costalotmore where each item is £ 5. No. of Items 1 2 3 4 Price (£’s) 5 10 15 20 Is this relationship directly proportional? How can we find out?

Look at Ratios We can look at the number of items and the cost of them in terms of their ratios. 1: 5, 2: 10, 3: 15 & 4: 20. What is the simplest form of each ratio? 1: 5 As the price increases at the same rate as the number of items, they are directly proportional.

Look at a graph

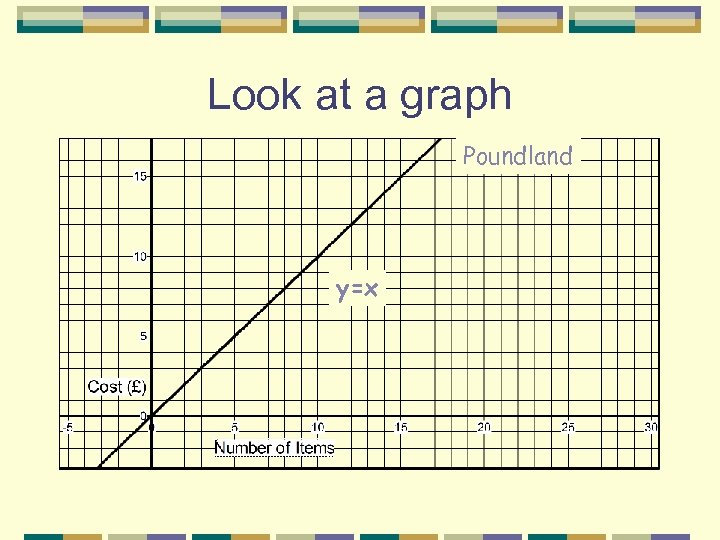Look at a graph Poundland y=x

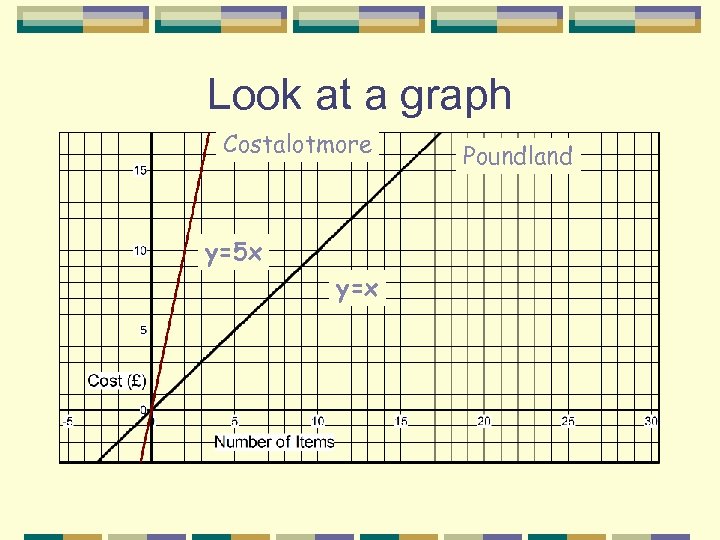Look at a graph Costalotmore y=5 x y=x Poundland

Notation α (alpha) α means proportional to or varies directly with. y α x means that y is directly proportional to, or varies with x.

Using the Notation In the first graph example y=x, this can be written as: yαx

In the second example y=5 x can also be written as: yαx Why?

General Equation The general equation for direct proportion is: y=kx where k is a constant amount and called the constant of proportion.

Example If y α x and y=2 when x=3, find the equation connecting y to x.

Solution using y = kx 1. Substitute values for x & y 2=kx 3 2. Re-arrange k = 2 3 3. Put it all back: y=2 x 3

Summary When 2 quantities are in direct proportion, as one quantity increases the other quantity increases at the same rate. y α x can be expressed as: y = kx

Non linear The examples so far have been linear, ie of the form: y=kx For non linear proportion, the general form becomes: y=kxn or y α kxn