Дипломний проект на тему Імовірнісно-стохастичний метод оптимізації радіаційного

Дипломний проект на тему Імовірнісно-стохастичний метод оптимізації радіаційного контролю навколишнього середовища АЕС Студента 4 курсу групи ТФ-1212 Філатова Г. Д.

Под полнотой контроля понимают наличие информации, необходимой для того, чтобы с вероятностью, не ниже заданной, определить уровни облучения людей и необходимые параметры радиационной обстановки в любой точке контролируемого пространства, в любой момент времени. Под достаточностью контроля понимают минимум информации, которая обеспечивает заданную полноту. Минимальный объем контроля, который обеспечивает нужную полноту, и будет минимально необходимым или достаточным объемом радиационного контроля.

Определение: Пространство контролируемо по списку параметров q 1. . . qn, если: - заданы контролируемые величины по каждому из параметров, как функции точки пространства qij 0( i, j), Pij 0( i, j), i, j ; - заданы контрольные уровни qi 0, Pi 0 -выполняется неравенство: Определение: Контроль достаточен по группе q 1. . . qm, с вероятностью P 0, если из условия не превышения параметрами q 1. . . qm, своих контрольных значений следует не превышение контрольных значений для каждого из параметров qm+1. . . qn, то есть: -

Структура индивидуальных эффективных доз характерных для АЭС с реакторами типа ВВЭР

Условие достаточности контроля: Если заданы контрольные величины измеряемых параметров (qi 0, Pi 0( )), и критерий достаточности P 0, то для достаточности контроля достаточно выполнения следующих неравенств: P 0 – заданная вероятность, D 0 – заданный допустимый уровень - контролируемое физическое пространство. Di(1) – дозовый коэффициент равный численному значению дозового показателя для единичного значения i-го параметра; qi 0 – контрольный уровень измеряемых значений; Pi 0 – доверительная вероятность того, что величина qi 0 попадает в интервал.

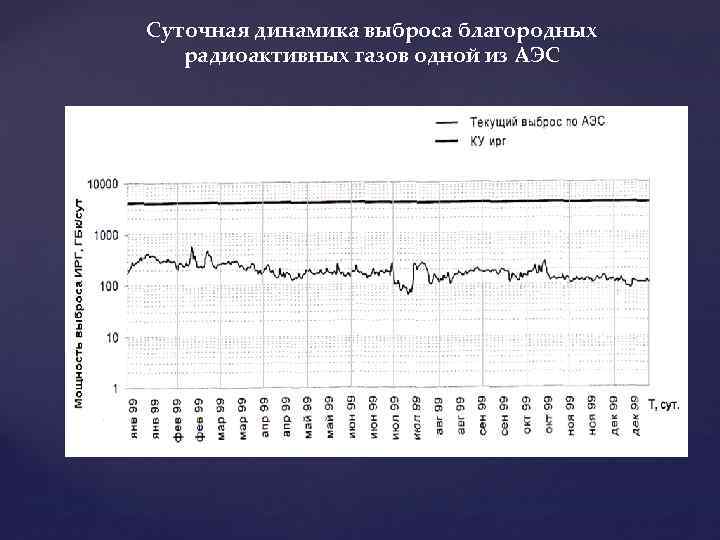Суточная динамика выброса благородных радиоактивных газов одной из АЭС

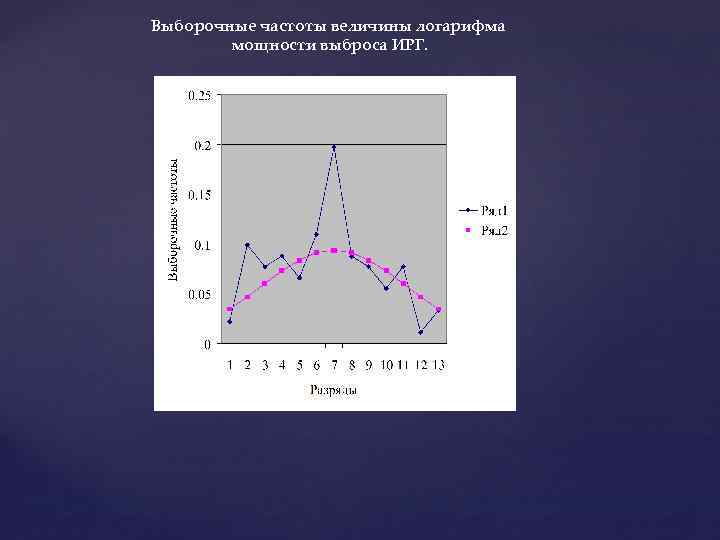Выборочные частоты величины логарифма мощности выброса ИРГ.

Где х, ξ – точки эвклидового пространства с координатами (xx, yx, zx) (xξ, yξ, 0ξ); qj(x) – концентрация j-радионуклида в точке х пространства; fj (|x ξ|) – функция ослабления потока ионизирующего излучения: воздушной средой zx≥ 0, грунтом для zx<0; BDj – дозовый фактор накопления в пространстве; Ω – область интегрирования, что в общем случае есть пространство. Концентрация в приземном шаре равняется q (xξ, yξ, 0+). Знак «+» означает, что берется концентрация в воздухе.

1. Выборочная функция распределения атмосферных параметров, от которых завысит радиоактивный параметр, продолжается непрерывной функцией распределения. При этом есть 2 альтернативных подхода. - непосредственное сглаживание с помощью метода наименьших квадратов; - построение непрерывной функции распределения. 2. Исходя из экспериментальных данных, находятся параметры распределения выброса. 3. Строится результирующая функция распределения функции от двух стохастических величин.

Для точки размещения поста контроля за фактическими данными повторяемости категорий стабильности строится распределение фактора метеорологического разведения (МР) на протяжении года. Если G – фактор (МР) в точке размещения поста контроля, то концентрация какого-либо радионуклида за определением фактора МР равняется QG где G рассчитывается по формуле:

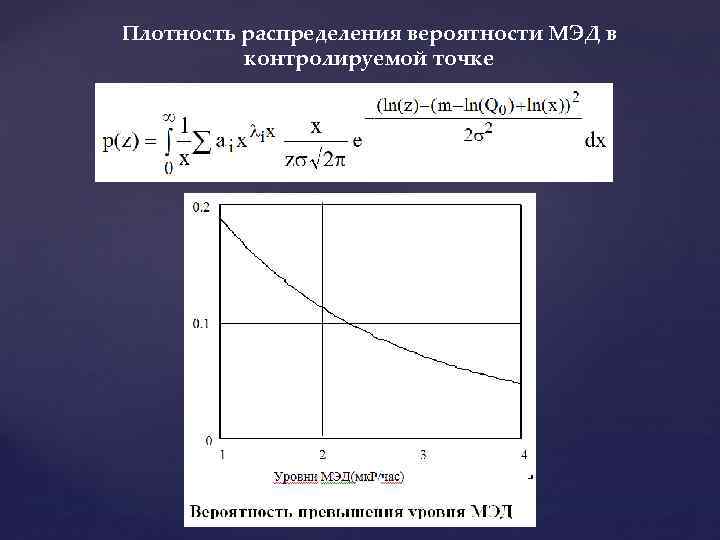Плотность распределения вероятности МЭД в контролируемой точке

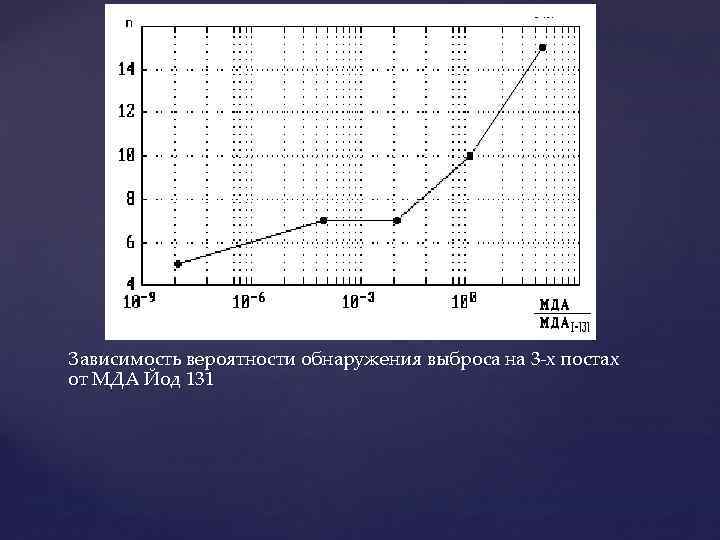Зависимость вероятности обнаружения выброса на 3 -х постах от МДА Йод 131

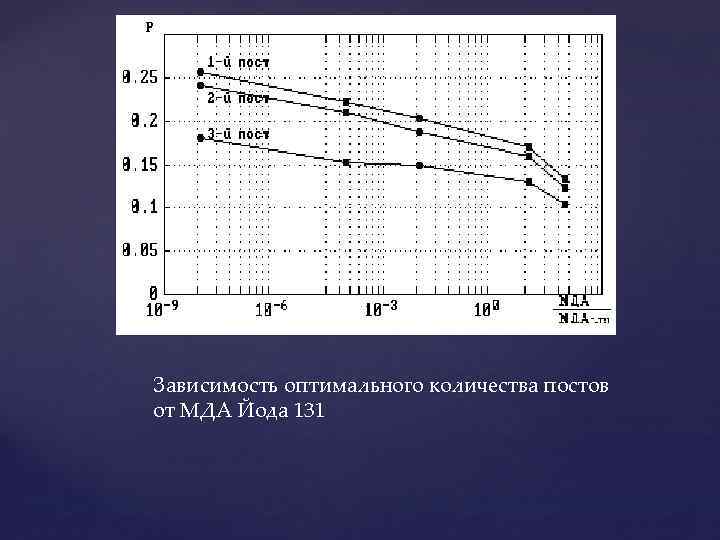Зависимость оптимального количества постов от МДА Йода 131

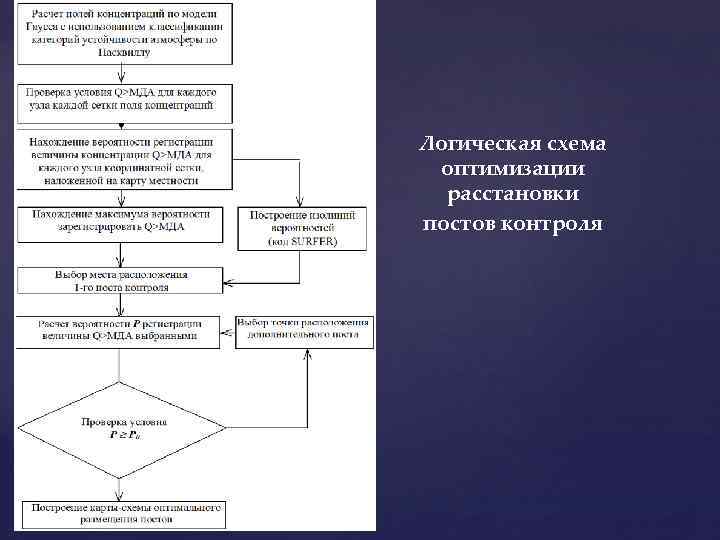Логическая схема оптимизации расстановки постов контроля

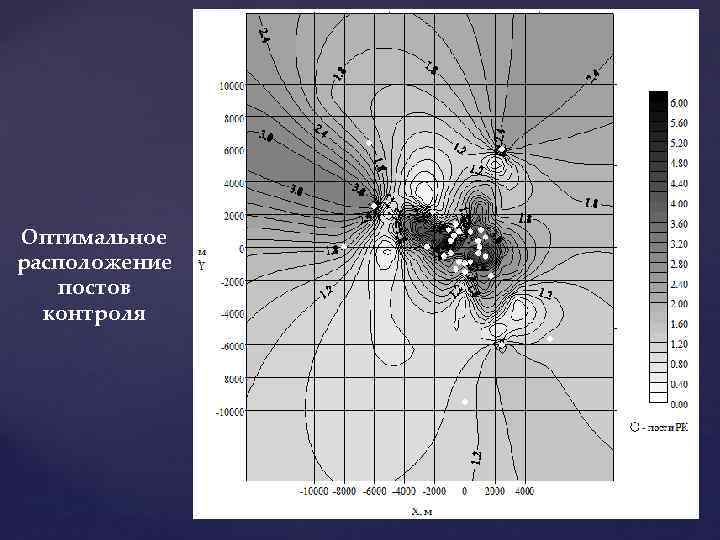Оптимальное расположение постов контроля

Поверхность вероятности (%) регистрации выброса Cs-137 одним постом