 Династия. Лекция 2 Повторение производных. Оптимизация. Метод Лагранжа. Введение понятия математического ожидания.
Династия. Лекция 2 Повторение производных. Оптимизация. Метод Лагранжа. Введение понятия математического ожидания.
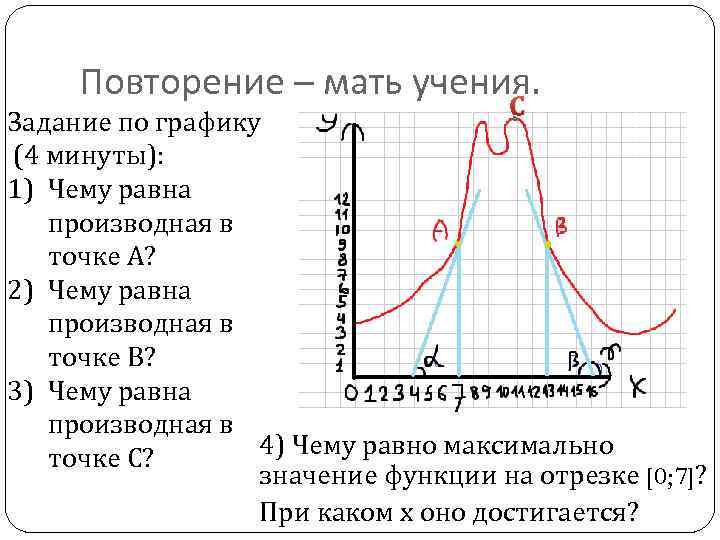 Повторение – мать учения. С Задание по графику (4 минуты): 1) Чему равна производная в точке А? 2) Чему равна производная в точке В? 3) Чему равна производная в 4) Чему равно максимально точке С? значение функции на отрезке [0; 7]? При каком х оно достигается?
Повторение – мать учения. С Задание по графику (4 минуты): 1) Чему равна производная в точке А? 2) Чему равна производная в точке В? 3) Чему равна производная в 4) Чему равно максимально точке С? значение функции на отрезке [0; 7]? При каком х оно достигается?
 Производные. Основные формулы
Производные. Основные формулы
 Производные. Основные формулы
Производные. Основные формулы
 Производная сложной функции Домашнее задание: доведите вычисления до конца
Производная сложной функции Домашнее задание: доведите вычисления до конца
 Оптимизация Процесс нахождения экстремума функции, т. е. выбор наилучшего варианта из множества возможных, процесс выработки оптимальных решений.
Оптимизация Процесс нахождения экстремума функции, т. е. выбор наилучшего варианта из множества возможных, процесс выработки оптимальных решений.
 Немного определений… Издержки TC — это оплата затрачиваемых ресурсов Доход (выручку) TR - денежные средства, полученные (вырученные) предприятием, фирмой, предпринимателем от продажи товаров и услуг Разность между доходом ТR и ее издержками TC равна прибыли PR, т. е. PR = TR - TC
Немного определений… Издержки TC — это оплата затрачиваемых ресурсов Доход (выручку) TR - денежные средства, полученные (вырученные) предприятием, фирмой, предпринимателем от продажи товаров и услуг Разность между доходом ТR и ее издержками TC равна прибыли PR, т. е. PR = TR - TC
 Оптимизируем? Однофакторная функция без ограничения Двухфакторная функция без ограничения Двухфакторная функция с ограничением => Лагранж
Оптимизируем? Однофакторная функция без ограничения Двухфакторная функция без ограничения Двухфакторная функция с ограничением => Лагранж
 Однофакторная функция без ограничения Пример Пусть издержки фирмы: Выручку можно найти по формуле: Тогда для прибыли фирмы имеем выражение: ИК
Однофакторная функция без ограничения Пример Пусть издержки фирмы: Выручку можно найти по формуле: Тогда для прибыли фирмы имеем выражение: ИК
 Пример Аналитическое решение задачи: используем условие первого порядка, т. е. найдем производную прибыли по переменной x и приравняем эту производную к нулю:
Пример Аналитическое решение задачи: используем условие первого порядка, т. е. найдем производную прибыли по переменной x и приравняем эту производную к нулю:
 Пример Что делать дальше? 1). Сравнить прибыли в точках 2). Использовать условие второго порядка, которое гласит, что если вторая производная прибыли по переменной x в точке x* отрицательна, то точка x* — точка максимума функции
Пример Что делать дальше? 1). Сравнить прибыли в точках 2). Использовать условие второго порядка, которое гласит, что если вторая производная прибыли по переменной x в точке x* отрицательна, то точка x* — точка максимума функции
 Пример Вывод: х=4
Пример Вывод: х=4
 Двухфакторная функция без ограничения Общий вид:
Двухфакторная функция без ограничения Общий вид:
 Появление ограничения. Появление Лагранжа. 2 типа задач: Постановка задачи: f(x 1, x 2) -> max p 1 x 1 +p 2 x 2 -> min при наличии ограничения: p 1 x 1 +p 2 x 2=V f(x 1, x 2) =U
Появление ограничения. Появление Лагранжа. 2 типа задач: Постановка задачи: f(x 1, x 2) -> max p 1 x 1 +p 2 x 2 -> min при наличии ограничения: p 1 x 1 +p 2 x 2=V f(x 1, x 2) =U
 1 задача: Строим функцию Лагранжа называется множителем Лагранжа. выписываем условие первого порядка Система имеет, как правило, единственное решение
1 задача: Строим функцию Лагранжа называется множителем Лагранжа. выписываем условие первого порядка Система имеет, как правило, единственное решение
 2 задача: Строим функцию Лагранжа все еще называется множителем Лагранжа. выписываем условие первого порядка Система имеет, как правило, единственное решение
2 задача: Строим функцию Лагранжа все еще называется множителем Лагранжа. выписываем условие первого порядка Система имеет, как правило, единственное решение
 Математическое ожидание
Математическое ожидание
 Спасибо за внимание. Домашнее задание будет выложена в группе ВК в 23 -59 (+-несколько минут) Также группа ВК перейдет в раздел закрытых.
Спасибо за внимание. Домашнее задание будет выложена в группе ВК в 23 -59 (+-несколько минут) Также группа ВК перейдет в раздел закрытых.