Динаміка валової продукції та факторів впливу на зміну

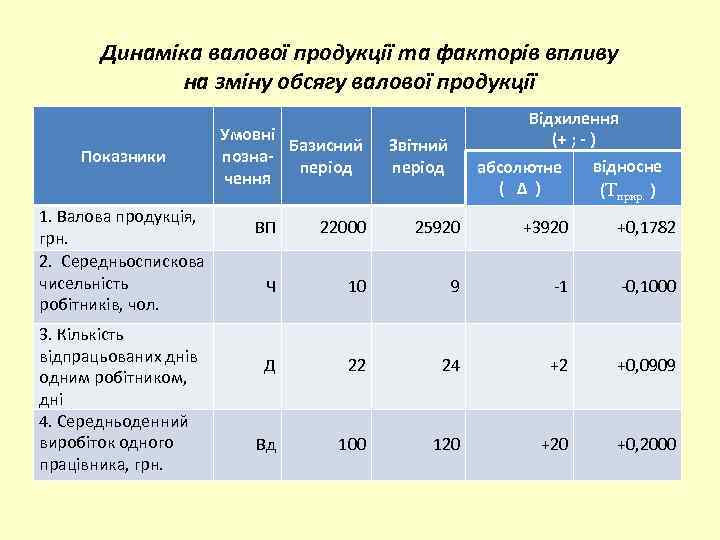Динаміка валової продукції та факторів впливу на зміну обсягу валової продукції Показники 1. Валова продукція, грн. 2. Середньоспискова чисельність робітників, чол. 3. Кількість відпрацьованих днів одним робітником, дні 4. Середньоденний виробіток одного працівника, грн. Умовні Базисний познаперіод чення Відхилення (+ ; - ) відносне абсолютне ( Δ ) (Тприр. ) Звітний період ВП 22000 25920 +3920 +0, 1782 Ч 10 9 -1 -0, 1000 Д 22 24 +2 +0, 0909 Вд 100 120 +0, 2000

Щоб визначити вплив кількісного фактору на результативний показник, необхідно відхилення кількісного фактору завжди множити на якісний плановий показник: ΔYкільк = Δxкільк × x 0 як Щоб визначити вплив якісного фактору на результативний показник, необхідно відхилення якісного фактору завжди множити на кількісний фактичний показник: ΔYяк = Δxяк × x 1 кільк

Особливості застосування способу ланцюгових підстановок Розрахунки ведуться в послідовній зміні базисних (планових) показників на звітні (фактичні). В першому розрахунку всі показники приймаються в базисному (плановому) значенні. В останньому розрахунку всі показники приймаються в звітному (фактичному) значенні.

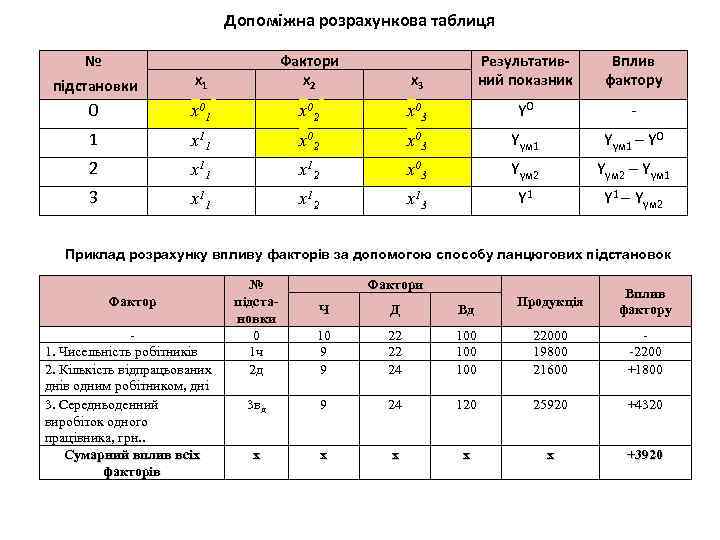Допоміжна розрахункова таблиця № підстановки x 1 Фактори x 2 x 3 Результативний показник Вплив фактору 0 x 0 1 x 0 2 x 0 3 Y 0 - 1 x 1 1 x 0 2 x 0 3 Yум 1 – Y 0 2 x 1 1 x 1 2 x 0 3 Yум 2 – Yум 1 3 x 1 1 x 1 2 x 1 3 Y 1 – Yум 2 Приклад розрахунку впливу факторів за допомогою способу ланцюгових підстановок Фактор 1. Чисельність робітників 2. Кількість відпрацьованих днів одним робітником, дні 3. Середньоденний виробіток одного працівника, грн. . Сумарний вплив всіх факторів № підстановки 0 1 ч 2 д Фактори Ч Д Вд 10 9 9 22 22 24 3 вд 9 х х Продукція Вплив фактору 100 100 22000 19800 21600 -2200 +1800 24 120 25920 +4320 х х х +3920

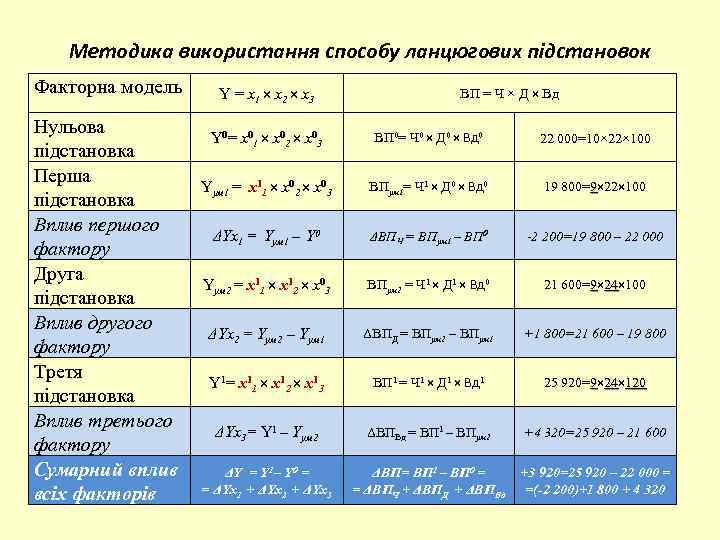Методика використання способу ланцюгових підстановок Факторна модель Нульова підстановка Перша підстановка Вплив першого фактору Друга підстановка Вплив другого фактору Третя підстановка Вплив третього фактору Сумарний вплив всіх факторів Y = x 1 × x 2 × x 3 ВП = Ч × Д × Вд Y 0= x 01 × x 02 × x 03 ВП 0= Ч 0 × Д 0 × Вд 0 22 000=10× 22× 100 Yум 1 = x 11 × x 02 × x 03 ВПум 1= Ч 1 × Д 0 × Вд 0 19 800=9× 22× 100 ΔYx 1 = Yум 1 – Y 0 ΔВПЧ = ВПум 1 – ВП 0 -2 200=19 800 – 22 000 Yум 2 = x 11 × x 12 × x 03 ВПум 2 = Ч 1 × Д 1 × Вд 0 21 600=9× 24× 100 24 ΔYx 2 = Yум 2 – Yум 1 ΔВПД = ВПум 2 – ВПум 1 +1 800=21 600 – 19 800 Y 1= x 11 × x 12 × x 13 ВП 1 = Ч 1 × Д 1 × Вд 1 25 920=9× 24× 120 24 ΔYx 3= Y 1 – Yум 2 ΔВПВд = ВП 1 – ВПум 2 +4 320=25 920 – 21 600 ΔY = Y 1– Y 0 = = ΔYx 1 + ΔYx 2 + ΔYx 3 ΔВП= ВП 1 – ВП 0 = +3 920=25 920 – 22 000 = = ΔВПЧ + ΔВПД + ΔВПВд =(-2 200)+1 800 + 4 320

Особливості застосування способу абсолютних різниць Є різновидом способу ланцюгових підстановок. Вплив першого фактору (кількісного) на результативний показник обчислюється множенням абсолютного приросту цього фактору на базисний рівень другого фактору (і всіх інших факторів, що включає модель). Вплив другого фактору на результативний показник обчислюється множенням фактичного значення першого фактору на абсолютний приріст другого фактору (тобто того фактору, вплив якого вивчається) та на базисний рівень третього фактору (і всіх інших, що включає модель). Вплив третього фактору (і всіх наступних) на результативний показник обчислюється множенням фактичного значення першого та другого факторів на абсолютний приріст третього фактору (тобто того фактору, вплив якого вивчається).

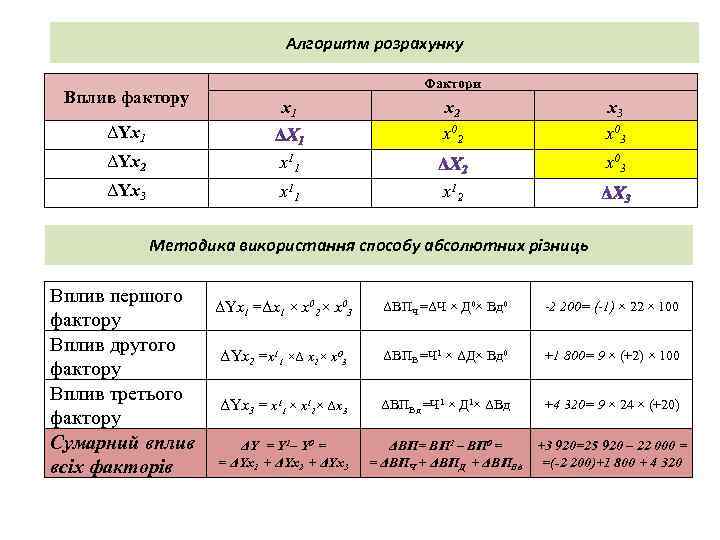Алгоритм розрахунку Вплив фактору Фактори x 1 ΔYx 2 x 1 1 x 3 x 0 3 x 1 1 ΔYx 3 x 2 x 0 3 x 1 2 Методика використання способу абсолютних різниць Вплив першого фактору Вплив другого фактору Вплив третього фактору Сумарний вплив всіх факторів ΔYx 1 =Δx 1 × x 02× x 03 ΔВПЧ =ΔЧ × Д 0× Вд 0 -2 200= (-1) × 22 × 100 ΔYx 2 =x 11 ×Δ x 2× x 03 ΔВПВ =Ч 1 × ΔД× Вд 0 +1 800= 9 × (+2) × 100 ΔYx 3 = x 11 × x 12× Δx 3 ΔВПВд =Ч 1 × Д 1× ΔВд +4 320= 9 × 24 × (+20) ΔY = Y 1– Y 0 = = ΔYx 1 + ΔYx 2 + ΔYx 3 ΔВП= ВП 1 – ВП 0 = +3 920=25 920 – 22 000 = = ΔВПЧ + ΔВПД + ΔВПВд =(-2 200)+1 800 + 4 320

Особливості застосування способу відносних різниць Вплив першого фактору (кількісного) на результативний показник обчислюється множенням базисного значення результативного показника на відносне відхилення першого фактору. Вплив другого фактору на результативний показник обчислюється множенням базисного значення результативного показника, скоригованого на вплив дії першого фактору на відносне відхилення другого фактору. Вплив третього фактору (і всіх наступних) на результативний показник обчислюється множенням базисного значення результативного показника, скоригованого на вплив дії першого і другого факторів на відносне відхилення третього фактору.

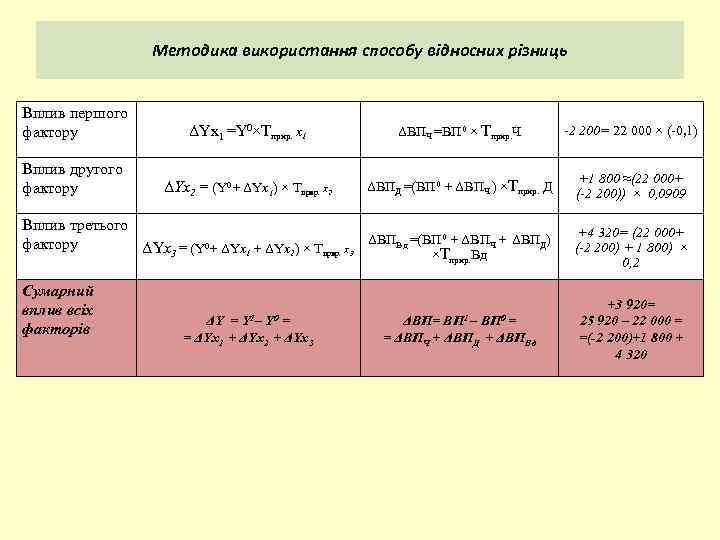Методика використання способу відносних різниць Вплив першого фактору ΔYx 1 =Y 0×Тприр. x 1 ΔВПЧ =ВП 0 × Тприр. Ч -2 200= 22 000 × (-0, 1) Вплив другого фактору ΔYx 2 = (Y 0+ ΔYx 1) × Тприр. x 2 ΔВПД =(ВП 0 + ΔВПЧ ) ×Тприр. Д +1 800 ≈(22 000+ (-2 200)) × 0, 0909 Вплив третього ΔВПВд =(ВП 0 + ΔВПЧ + ΔВПД) 0+ ΔYx ) × Т фактору ΔYx 3= (Y прир. x 3 1 2 ×Т Вд прир. Сумарний вплив всіх факторів ΔY = Y 1– Y 0 = ΔВП= ВП 1 – ВП 0 = = ΔYx 1 + ΔYx 2 + ΔYx 3 = ΔВПЧ + ΔВПД + ΔВПВд +4 320= (22 000+ (-2 200) + 1 800) × 0, 2 +3 920= 25 920 – 22 000 = =(-2 200)+1 800 + 4 320

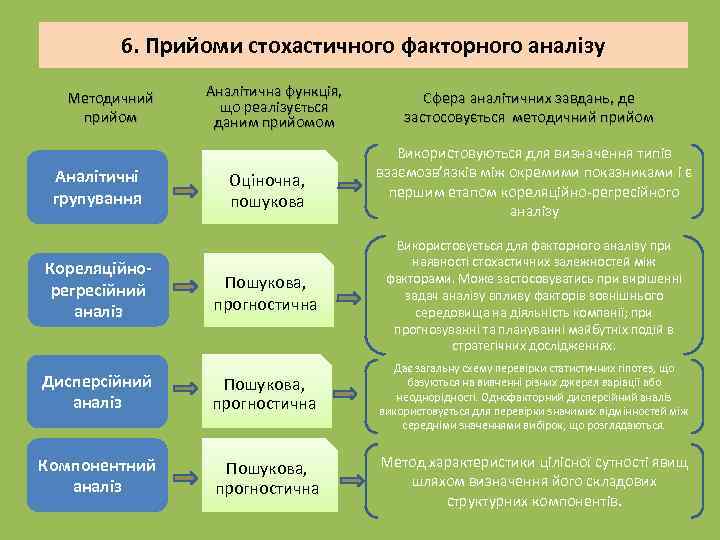6. Прийоми стохастичного факторного аналізу Методичний прийом Аналітичні групування Аналітична функція, що реалізується даним прийомом Оціночна, пошукова Сфера аналітичних завдань, де застосовується методичний прийом Використовуються для визначення типів взаємозв’язків між окремими показниками і є першим етапом кореляційно-регресійного аналізу Пошукова, прогностична Використовується для факторного аналізу при наявності стохастичних залежностей між факторами. Може застосовуватись при вирішенні задач аналізу впливу факторів зовнішнього середовища на діяльність компанії; при прогнозуванні та плануванні майбутніх подій в стратегічних дослідженнях. Дисперсійний аналіз Пошукова, прогностична Дає загальну схему перевірки статистичних гіпотез, що базуються на вивченні різних джерел варіації або неоднорідності. Однофакторний дисперсійний аналіз використовується для перевірки значимих відмінностей між середніми значеннями вибірок, що розглядаються. Компонентний аналіз Пошукова, прогностична Метод характеристики цілісної сутності явищ шляхом визначення його складових структурних компонентів. Кореляційнорегресійний аналіз

7. Методичні прийоми перспективного дослідження, що використовуються в стратегічному аналізі Стратегічний аналіз – це система процедур дослідження економічних явищ і процесів, які впливають на діяльність суб’єкта господарювання в минулому, поточному та в майбутньому періодах майбутньому як на мікро-, так і на макрорівні (тобто з урахуванням впливу зовнішнього середовища). зовнішнього середовища Ці процедури формують інформаційне поле для виконання тактичних дій, спрямованих на досягнення стратегічних цілей.

Складові стратегічного аналізу Внутрішній аналіз передбачає діагностику стратегічного потенціалу в рамках поставленої мети, оцінку ефективності обраних стратегій, обґрунтування найбільш раціональних шляхів виконання поставлених стратегічних цілей. В межах внутрішнього стратегічного аналізу визначають відповідність системи управління, достатність ресурсів, кваліфікації персоналу цільовим вимогам та завданням, тобто проводиться аналіз фактичного і необхідного потенціалу організації для досягнення обраної стратегії. Зовнішній аналіз передбачає дослідження середовища функціонування об’єкту дослідження. Його методичні підходи суттєво відрізняються в залежності від рівня оточення (безпосереднє оточення, мезо- та мега-середовище). При проведенні зовнішнього аналізу основними аспектами дослідження мають бути: аналіз конкурентів та контрагентів; оцінка конкурентної позиції підприємства за окремими сегментами ринку; маркетинговий аналіз; аналіз ринку капіталів та ресурсів; аналіз ринку технологій; аналіз впливу політичних, соціальних, географічних, правових факторів (інфляції, сальдо платіжного балансу, рівень зайнятості населення, тенденції зміни обсягу іноземних інвестицій) на поточну стратегію та перспективи розвитку підприємства, а також та його конкурентів та контрагентів. На стику внутрішнього та зовнішнього аналізу проводиться аналіз конкурентоспроможності та конкурентних переваг шляхом з‘ясування сильних і слабких сторін організації, визначення його конкурентної позиції на ринку.

Прийоми прогнозування 1. Якiсні. Базовані на освiченій думці, iнтуїцiї й досвiді професiоналiв. Серед його рiзновидiв: консенсус керiвництва, метод Дельфi, оцiнка торговими працiвниками (кожного по своєму регiону), опитування клiєнтiв. 2. Кiлькiсні. Базовані на математичних моделях й iсторичних даних: 2. 1. причинно-наслiдковi моделі; 2. 2. моделі часових рядів: q моделі сезонності й тренду; q моделі згладжування: § рухома середня (проста, зважена); § експоненційне згладжування. .

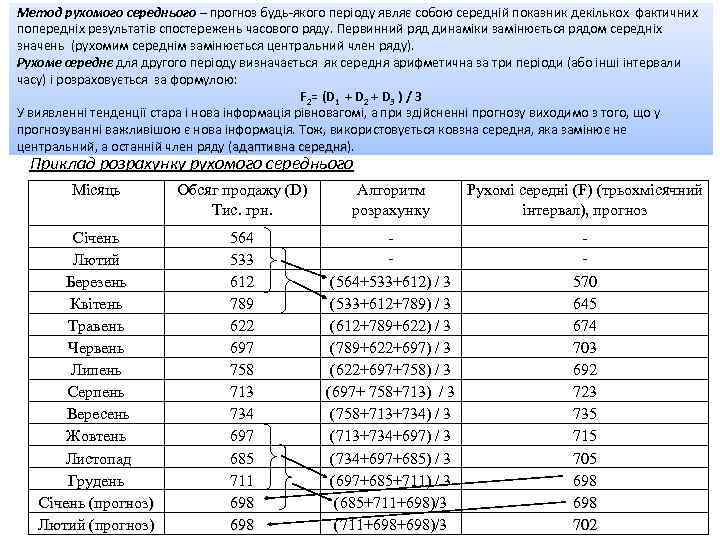Метод рухомого середнього – прогноз будь-якого періоду являє собою середній показник декількох фактичних попередніх результатів спостережень часового ряду. Первинний ряд динаміки замінюється рядом середніх значень (рухомим середнім замінюється центральний член ряду). Рухоме середнє для другого періоду визначається як середня арифметична за три періоди (або інші інтервали часу) і розраховується за формулою: F 2= (D 1 + D 2 + D 3 ) / 3 У виявленні тенденції стара і нова інформація рівновагомі, а при здійсненні прогнозу виходимо з того, що у прогнозуванні важливішою є нова інформація. Тож, використовується ковзна середня, яка замінює не центральний, а останній член ряду (адаптивна середня). адаптивна середня Приклад розрахунку рухомого середнього Місяць Обсяг продажу (D) Тис. грн. Алгоритм розрахунку Рухомі середні (F) (трьохмісячний інтервал), прогноз Січень Лютий Березень Квітень Травень Червень Липень Серпень Вересень Жовтень Листопад Грудень Січень (прогноз) Лютий (прогноз) 564 533 612 789 622 697 758 713 734 697 685 711 698 - - (564+533+612) / 3 (533+612+789) / 3 (612+789+622) / 3 (789+622+697) / 3 (622+697+758) / 3 (697+ 758+713) / 3 (758+713+734) / 3 (713+734+697) / 3 (734+697+685) / 3 (697+685+711) / 3 (685+711+698)/3 (711+698)/3 570 645 674 703 692 723 735 715 705 698 702

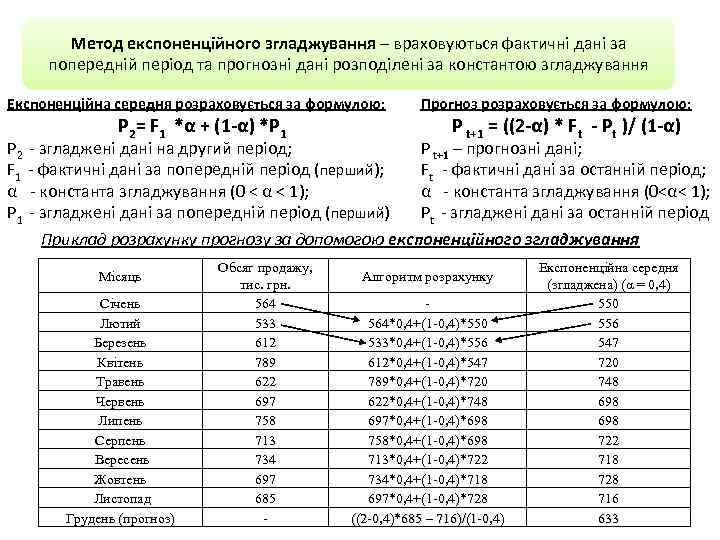Метод експоненційного згладжування – враховуються фактичні дані за попередній період та прогнозні дані розподілені за константою згладжування Експоненційна середня розраховується за формулою: Прогноз розраховується за формулою: P 2 - згладжені дані на другий період; F 1 - фактичні дані за попередній період (перший); α - константа згладжування (0 < α < 1); P 1 - згладжені дані за попередній період (перший) P t+1 – прогнозні дані; Ft - фактичні дані за останній період; α - константа згладжування (0<α< 1); Pt - згладжені дані за останній період P 2= F 1 *α + (1 -α) *P 1 P t+1 = ((2 -α) * Ft - Pt )/ (1 -α) Приклад розрахунку прогнозу за допомогою експоненційного згладжування Місяць Січень Лютий Березень Квітень Травень Червень Липень Серпень Вересень Жовтень Листопад Грудень (прогноз) Обсяг продажу, тис. грн. 564 533 612 789 622 697 758 713 734 697 685 - Алгоритм розрахунку 564*0, 4+(1 -0, 4)*550 533*0, 4+(1 -0, 4)*556 612*0, 4+(1 -0, 4)*547 789*0, 4+(1 -0, 4)*720 622*0, 4+(1 -0, 4)*748 697*0, 4+(1 -0, 4)*698 758*0, 4+(1 -0, 4)*698 713*0, 4+(1 -0, 4)*722 734*0, 4+(1 -0, 4)*718 697*0, 4+(1 -0, 4)*728 ((2 -0, 4)*685 – 716)/(1 -0, 4) Експоненційна середня (згладжена) (α = 0, 4) 550 556 547 720 748 698 722 718 728 716 633

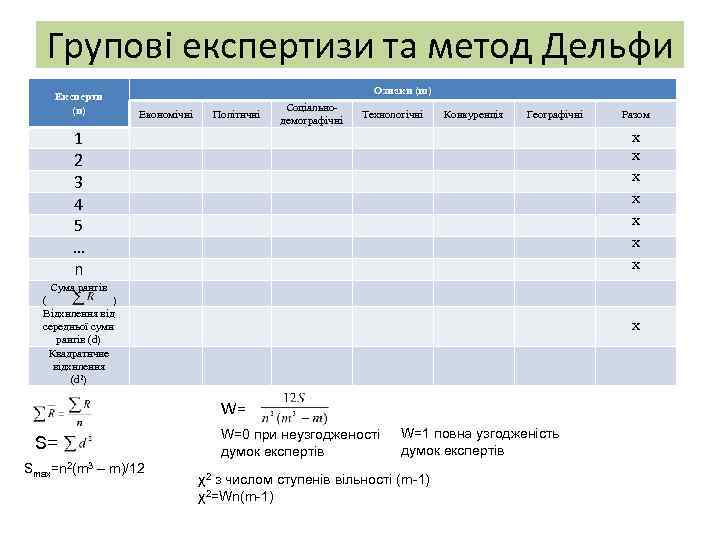Групові експертизи та метод Дельфи Експерти (n) Ознаки (m) Економічні Політичні Соціальнодемографічні Технологічні Конкуренція Географічні 1 2 3 4 5 … n Х Х Х Х Сума рангів ( ) Відхилення від середньої суми рангів (d) Квадратичне відхилення (d 2) Х W= S= Smax=n 2(m 3 – m)/12 Разом W=0 при неузгодженості думок експертів W=1 повна узгодженість думок експертів χ2 з числом ступенів вільності (m-1) χ2=Wn(m-1)

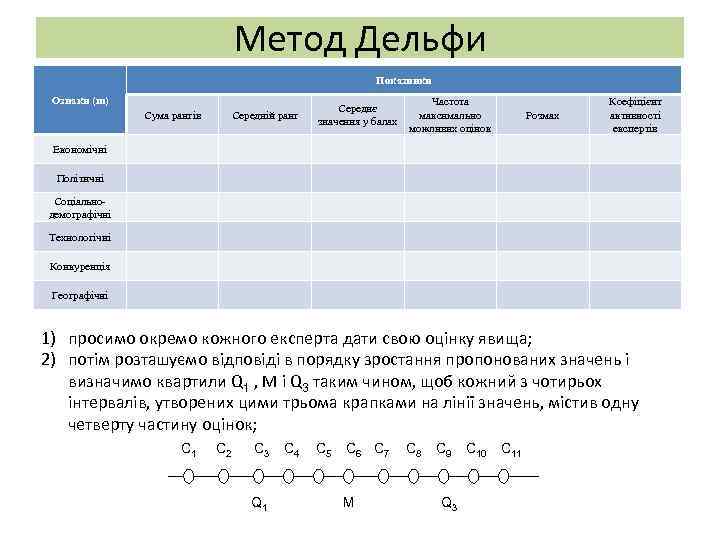Метод Дельфи Показники Ознаки (m) Сума рангів Середній ранг Середнє значення у балах Частота максимально можливих оцінок Розмах Коефіцієнт активності експертів Економічні Політичні Соціальнодемографічні Технологічні Конкуренція Географічні 1) просимо окремо кожного експерта дати свою оцінку явища; 2) потім розташуємо відповіді в порядку зростання пропонованих значень і визначимо квартили Q 1 , M і Q 3 таким чином, щоб кожний з чотирьох інтервалів, утворених цими трьома крапками на лінії значень, містив одну четверту частину оцінок; С 1 С 2 С 3 Q 1 С 4 С 5 С 6 С 7 M С 8 С 9 Q 3 С 10 С 11

3) значення Q 1, M і Q 3 (думка експертної групи) повідомляємо учасникам опитування. У тому випадку, якщо первісна оцінка виходить за міжквартильне значення (Q 1 - Q 3), просимо переглянути її, а також висловити свої розуміння, чому відповідь повинна бути нижче (чи вище) значень, визначених 75% учасників першого туру; 4) передаємо результати другого туру (які, як правило, мають меншу розбіжність, чим у першому турі) в узагальненій формі всім учасникам опитування, включаючи сюди нові квартилі і медіану. Крім того, фіксуємо обґрунтування зменшення чи збільшення значень, запропонованих учасникам опитування в другому турі (звичайно, при їхньому узагальненні і редагуванні зберігається анонімність авторів); 5) просимо розглянути нові оцінки і їхні обґрунтування, висловити свій сумнів про їхню вагомість і переглянути свою попередню оцінку. У тому випадку, якщо переглянуті оцінки випадають з міжквартильних значень, то автора просять коротко викласти причини його незгоди з аргументами, що привели б його оцінку ближче до значення медіани; 6) у четвертому турі учасникам опитування повідомляють квартили третього розподілу відповідей і контраргументи, висловлені в третьому турі і просять ще раз переглянути оцінки. Медіана, одержувана в результаті четвертого туру, приймається як значення групової експертної оцінки величини попиту. Найчастіше необхідний рівень консенсусу експертів досягається за два тури.

Експертне оцінювання методом попарних порівнянь Експерти використовують дві оцінки: 0 або 1. Більш вагомому варіанту надається оцінка 1, менш вагомому — 0. Результати попарних порівнянь оформляються у вигляді матриці, елементами якої є кількості наданих переваг aij, n – кількість експертів Варіант А В А 0 1 В 4 0 С 5 4 Разом 9 5 i 0, 60 0, 33 С 0 1 0, 07 Разом 1 5 9 15 1, 00 Відношення кількості наданих відповідному варіанту переваг до загальної суми елементів матриці характеризує його вагомість

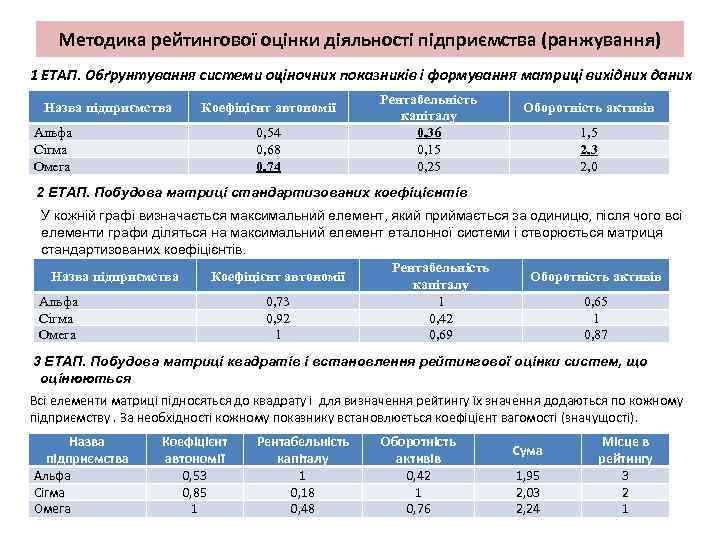Методика рейтингової оцінки діяльності підприємства (ранжування) 1 ЕТАП. Обґрунтування системи оціночних показників і формування матриці вихідних даних Назва підприємства Коефіцієнт автономії Альфа Сігма Омега 0, 54 0, 68 0, 74 Рентабельність капіталу 0, 36 0, 15 0, 25 Оборотність активів 1, 5 2, 3 2, 0 2 ЕТАП. Побудова матриці стандартизованих коефіцієнтів У кожній графі визначається максимальний елемент, який приймається за одиницю, після чого всі елементи графи діляться на максимальний елемент еталонної системи і створюється матриця стандартизованих коефіцієнтів. Рентабельність Назва підприємства Коефіцієнт автономії Оборотність активів капіталу Альфа 0, 73 1 0, 65 Сігма 0, 92 0, 42 1 Омега 1 0, 69 0, 87 3 ЕТАП. Побудова матриці квадратів і встановлення рейтингової оцінки систем, що оцінюються Всі елементи матриці підносяться до квадрату і для визначення рейтингу їх значення додаються по кожному підприємству. За необхідності кожному показнику встановлюється коефіцієнт вагомості (значущості). Назва підприємства Альфа Сігма Омега Коефіцієнт автономії 0, 53 0, 85 1 Рентабельність капіталу 1 0, 18 0, 48 Оборотність активів 0, 42 1 0, 76 Сума 1, 95 2, 03 2, 24 Місце в рейтингу 3 2 1

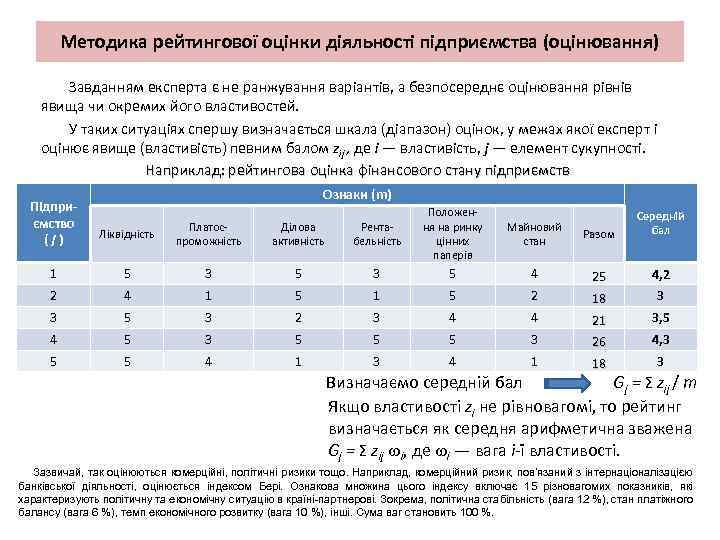Методика рейтингової оцінки діяльності підприємства (оцінювання) Завданням експерта є не ранжування варіантів, а безпосереднє оцінювання рівнів явища чи окремих його властивостей. У таких ситуаціях спершу визначається шкала (діапазон) оцінок, у межах якої експерт і оцінює явище (властивість) певним балом zij , де i — властивість, j — елемент сукупності. Наприклад: рейтингова оцінка фінансового стану підприємств Підприємство (j) Ознаки (m) Ліквідність Платоспроможність Ділова активність Рентабельність Положення на ринку цінних паперів Майновий стан Разом Середній бал 1 5 3 5 4 25 4, 2 2 4 1 5 2 18 3 3 5 3 2 3 4 4 21 3, 5 4 5 3 5 5 5 3 26 4, 3 5 5 4 1 3 4 1 18 3 Визначаємо середній бал Gj = Σ zij / m Якщо властивості zi не рівновагомі, то рейтинг визначається як середня арифметична зважена Gj = Σ zij i, де i — вага i-ї властивості. Зазвичай, так оцінюються комерційні, політичні ризики тощо. Наприклад, комерційний ризик, пов’язаний з інтернаціоналізацією банківської діяльності, оцінюється індексом Бері. Ознакова множина цього індексу включає 15 різновагомих показників, які характеризують політичну та економічну ситуацію в країні-партнерові. Зокрема, політична стабільність (вага 12 %), стан платіжного балансу (вага 6 %), темп економічного розвитку (вага 10 %), інші. Сума ваг становить 100 %.