ДИНАМИКА ТВЕРДОГО ТЕЛА ЛЕКЦИЯ 5: ПЛОСКОЕ ДВИЖЕНИЕ ТВЕРДОГО

ДИНАМИКА ТВЕРДОГО ТЕЛА ЛЕКЦИЯ 5: ПЛОСКОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА

1. Уравнения движения При плоскопараллельном движении точки тела движутся в плоскостях, параллельных некоторой неподвижной (основной) плоскости. Движение = движение центра масс+ вращение относительно центра масс Центр масс движется параллельно неподвижной плоскости, а движение относительно центра масс есть вращение тела вокруг оси, проходящей через центр масс и перпендикулярной к неподвижной плоскости. Положение тела определено если известны Теорема о движении центра масс Уравнения для нахождения Теорема об изменении момента количеств движения

2. Использование теоремы об изменении кинетической энергии При интегрировании системы уравнений движения можно эти уравнения заменять другими, получающимися в результате их взаимных комбинаций. В частности, иногда удобно использовать теорему об изменении кинетической энергии По теореме Кенига кинетическая энергия равна По теореме об изменении кинетической энергии Изменение кинетической энергии = Работа внешних сил

3. Использование теоремы моментов для оси z неподвижной системы Кинетический момент относительно неподвижного центра О равен сумме кинетического момента центра масс, в котором сосредоточена масса тела, относительно центра О и кинетического момента тела относительно центра С в его движении по отношению к системе осей, проходящих через центр масс и перемещающихся поступательно

4. Пример 1: скольжение цилиндра по наклонной плоскости Тяжелый круглый цилиндр движется, касаясь абсолютно гладкой наклонной плоскости, так, что ось цилиндра остается все время горизонтальной. Движение происходит параллельно вертикальной плоскости, перпендикулярной к оси цилиндра. Найти уравнения движения цилиндра. Уравнения движения Уравнения связи Цилиндр вращается с постоянной угловой скростью ему в начальный момент и движется с постоянным ускорением , сообщенной

5. Пример 2: качение цилиндра без проскальзывания Тяжелый круглый цилиндр катится по шероховатой наклонной плоскости без скольжения. Исследовать движение цилиндра. Уравнения движения Уравнения связи 1 Уравнения связи 2 Для однородного цилиндра Когда возможно такое движение?

6. Пример 3: качение цилиндра с проскальзыванием Тяжелый круглый цилиндр катится по шероховатой наклонной плоскости. Исследовать движение цилиндра. Уравнения движения Уравнения связи 1 Уравнения связи 2

7. Пример 4: качение цилиндра со сдвинутым центром тяжести Неоднородный диск катится без скольжения по неподвижной горизонтальной плоскости. Масса диска равна m, радиус a, центр масс С находится на расстоянии b от геометрического центра, момент инерции относительно оси, перпендикулярной плоскости диска и проходящей через его центр масс, равен Ic. Получить дифференциальные уравнения движения диска. Уравнения движения

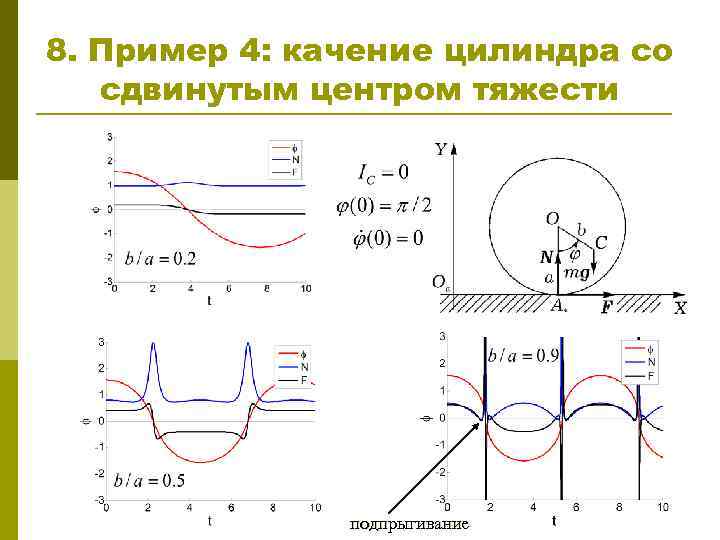8. Пример 4: качение цилиндра со сдвинутым центром тяжести подпрыгивание

9. Пример 5: падение стержня Однородный стержень массы m и длины 2 l расположен вертикально. Нижний конец опирается на гладкую плоскость. После того как ему задали бесконечно малое смещение от вертикали он начал падать. Получить ДУ движения. 1) Горизонтальных сил нет. Центр масс падает вертикально 2) Закон сохранения энергии 3) Уравнение связи

10. Пример 5: падение стержня Горизонтальная скорость имеет максимум

11. Пример 6: падение стержня Тонкий однородный стержень приставлен одним концом к гладкой вертикальной стене, а другим концом опирается на гладкий пол. Стержень пришел в движение из состояния покоя, когда он составлял угол с вертикалью. Вычислить начальные давления на стену и пол.

12. Пример 6: падение стержня