Динамика – третий раздел теоретической механики, в котором

Динамика – третий раздел теоретической механики, в котором изучается механическое движение материальных тел с учетом их механического взаимодействия и механическое взаимодействие материальных тел при их механическом движении. В основе теоретической, как и всей классической механики, лежат аксиомы (законы) Галилея – Ньютона, сформулированные для простейшей модели материального тела – материальной точки. Аксиомы классической механики были изложены Ньютоном в его труде «Математические начала натуральной философии» , опубликованном в 1687 году. Аксиомы выполняются относительно инерциальных систем отсчета. В роли инерциальной системы отсчета используется гелиоцентрическая система, начало которой в центре Солнца, а оси направлены на одни и те же звезды. Как показывает опыт, это не приводит к заметным погрешностям. 1

Основные аксиомы классической механики • Первая аксиома – закон инерции • Если система сил, приложенных к материальной точке, уравновешена, то точка движется равномерно и прямолинейно (по инерции) или сохраняет состояния покоя относительно инерциальной системы отсчета. • Вторая аксиома – закон изменения • Изменение движения пропорционально приложенной движущей силе и происходит в направлении линии действия этой силы относительно инерциальной системы отсчета. 2

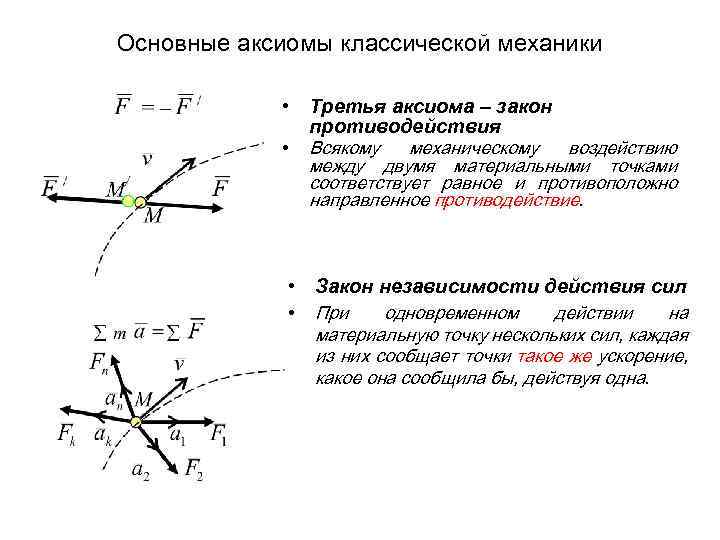Основные аксиомы классической механики • Третья аксиома – закон противодействия • Всякому механическому воздействию между двумя материальными точками соответствует равное и противоположно направленное противодействие. • Закон независимости действия сил • При одновременном действии на материальную точку нескольких сил, каждая из них сообщает точки такое же ускорение, какое она сообщила бы, действуя одна.

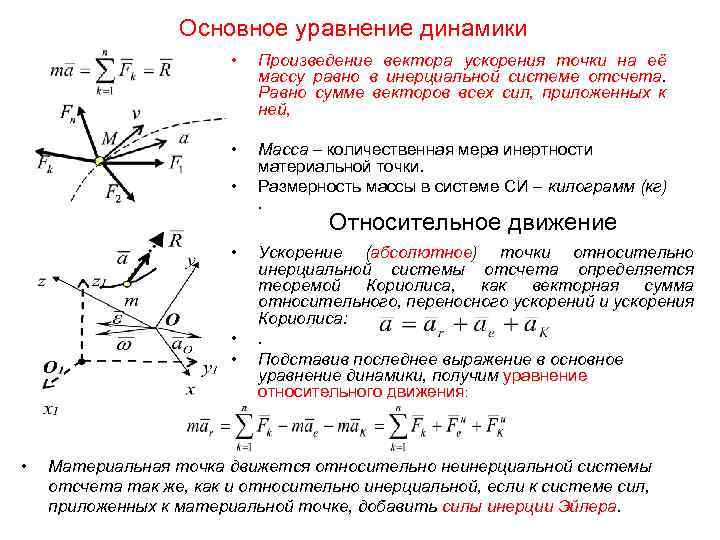Основное уравнение динамики • Произведение вектора ускорения точки на её массу равно в инерциальной системе отсчета. Равно сумме векторов всех сил, приложенных к ней, • Масса – количественная мера инертности материальной точки. Размерность массы в системе СИ – килограмм (кг). • Относительное движение • • Ускорение (абсолютное) точки относительно инерциальной системы отсчета определяется теоремой Кориолиса, как векторная сумма относительного, переносного ускорений и ускорения Кориолиса: . Подставив последнее выражение в основное уравнение динамики, получим уравнение относительного движения: Материальная точка движется относительно неинерциальной системы отсчета так же, как и относительно инерциальной, если к системе сил, приложенных к материальной точке, добавить силы инерции Эйлера.

• Сравнивая силы инерции Эйлера с силой тяжести тел, можно оценить погрешность «инерциальности» системы отсчета, связанной с поверхностью Землей. : • При движении по инерции материальной точки относительно Земли со скоростью (vr=330 м/с) звука , сила инерции Кориолиса не превышает десятых долей процента её веса: a. K=2 evr=0, 048 0, 5%g, так как угловая скорость вращения Земли e = 0, 727*10 -4 c-1, а g=9, 81 м/с2 • . Переносная сила инерции материальной точки, покоящейся на экваторе Земли, не превышает десятых долей процента её веса: ae = 2 e R =0, 034 0, 3%g, так как радиус Земли R = 6, 4*106 м Принцип относительности Галилея – Ньютона • Все механические явления в различных инерциальных системах отсчета протекают одинаково. Любая система отсчета, перемещающаяся равномерно прямолинейно относительно инерциальной системы отсчета, является инерциальной системой отсчета. Две основные задачи динамики • 1 -ая прямая задача: Зная механическое движение материальной точки, определить механическое воздействие, оказываемое на неё. • 2 -ая обратная задача: Зная механическое воздействие, оказываемое на материальную точку, и начальные условия её движения определить её механическое движение.

Дифференциальные уравнения движения точки • • Определить механическое движение материальной точки M – это, значит, найти функциональную зависимость координат движущейся точки от времени: x = x(t), y = y(t), z = z(t) • • Принципиальным отличием обратных задач динамики является то, что после проецирования основного уравнения динамики на координатные оси они сводятся к решению дифференциальных уравнений Спроецировав основное уравнение динамики на оси введенной прямоугольной декартовой системы координат Oxyz, и, учтя, что проекция вектора ускорения точки на любую ось равна второй производной по времени от соответствующей координаты движущейся точки, получим дифференциальные уравнения движения точки Произведение массы движущейся материальной точки на вторую производную по времени от любой её координаты равно сумме проекций всех сил, действующих на точку, на соответствующую ось. Неопределенные постоянные после дважды проведенного интегрирования дифференциальных уравнений движения точки, как правило, определяются из начальных условий движения точки Три координаты M 0(x 0, y 0, z 0) и три проекции вектора скорости (v 0 x, v 0 y, v 0 z), определяющие положение точки и её скорость в начальный момент времени t 0: . x 0= x(t 0), y 0=y(t 0), z 0, =z(t 0), v 0 x=(t 0), v 0 y=(t 0), v 0 z=(t 0)

Пример решения прямой задачи динамики • Груз массой m движется вверх по негладкой поверхности (коэффициент трения скольжения f), наклоненной к горизонту под углом (sin =0. 6). Определить величину силы G, толкающей груз вверх вдоль поверхности с ускорением a • • • Дано: m=0, 5 кг, f=0, 25, a=2 м/с2. Найти G. Решение: • • 1. ОИ – груз. МИ - ОУД. 2. КХ: ИСО – прямоугольная система координат 0 xy связана с неподвижной поверхностью. Ось 0 x вверх вдоль поверхности. v и a – проекции скорости и ускорения груза на ось 0 x. : • 3 СС: G – толкающая вдоль поверхности сила, mg – сила тяжести вертикально вниз, N – нормальная реакция перпендикулярно поверхности, F – сила трения скольжения противоположно скорости. Величина силы трения по закону Амонтона: • 4 МИ: для груза составим основное уравнение динамики: 5. Спроецируем ОУД на оси выбранной системы координат: Определим величину силы G, толкающей груз вверх вдоль поверхности =0, 5*(2+10*0, 6+0, 25*10*0, 8)=6 Н

Пример решения обратной задачи динамики • Груз массой m движется вверх по негладкой поверхности (коэффициент трения скольжения f), наклоненной к горизонту под углом (sin =0. 6), под действием силы G, толкающей груз вверх вдоль поверхности. Какой путь груз пройдет до остановки, если его начальная скорость v 0. • • • Дано: m=0. 5 кг, f=0, 25, G =3 Н, v 0. =4 м/с. Найти S 1=S(t 1), если v 1=v(t 1)=0. Решение: • • 1. ОИ – груз. МИ - дифференциальное уравнение движения точки. 2. КХ: ИСО – прямоугольная система координат 0 xy связана с неподвижной поверхностью. Ось 0 x вверх вдоль поверхности. Начало оси там, где v=v 0. В произвольный момент времени t положение груза. определяется координатой x. • 3 СС: G – толкающая вдоль поверхности сила, mg – сила тяжести вертикально вниз, N – нормальная реакция перпендикулярно поверхности, F – сила трения скольжения противоположно скорости. Величина силы трения, как в предыдущей задаче, равна: • 4 МИ: составим для груза дифференциальное уравнение и начальные условия движения : 5. Подставив данные, применив методы понижения степени и разделения переменных, проинтегрируем дважды полученное дифференциальное уравнение. Определив постоянные интегрирования из начальных условий, получим уравнение движения груза и закон изменения его скорости: Определим путь, который груз пройдет до остановки: t 1=4/2=2 c, S 1 =4*2 -22 =4 м.

Виды дифференциальных уравнений и их решение Начальные условия: Сила тяжести Сила сопротивления Сила упругости – Сила вынуждающая - Название задачи , Свободное падение Сопротивление при падении Свободные колебания Затухающие колебания Вынужденные колебания Диф. уравнение Уравнение движения

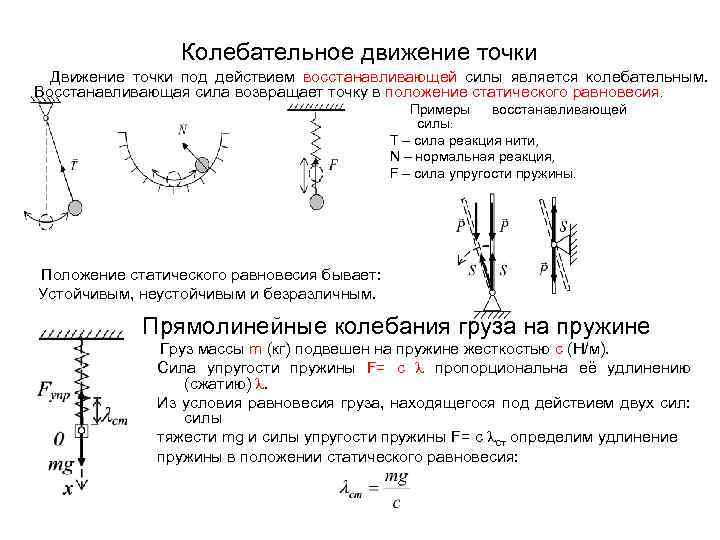Колебательное движение точки Движение точки под действием восстанавливающей силы является колебательным. Восстанавливающая сила возвращает точку в положение статического равновесия. Примеры восстанавливающей силы: T – сила реакция нити, N – нормальная реакция, F – сила упругости пружины. Положение статического равновесия бывает: Устойчивым, неустойчивым и безразличным. Прямолинейные колебания груза на пружине Груз массы m (кг) подвешен на пружине жесткостью c (Н/м). Сила упругости пружины F= c пропорциональна её удлинению (сжатию) . Из условия равновесия груза, находящегося под действием двух сил: силы тяжести mg и силы упругости пружины F= c ст определим удлинение пружины в положении статического равновесия:

Свободные колебания материальной точки • • 1. ОИ – точка. МИ - дифференциальное уравнение свободных колебаний точки. 2. КХ: ИСО – ось 0 x вертикально вниз. Начало оси в положении статического равновесия. В начальный момент времени t 0=0 положение и скорость точки. определяются координатой x(0)=x 0 и проекцией скорости vx(0)=v 0. В произвольный момент времени t положение груза. определяется координатой x 3 СС: mg – сила тяжести точки вертикально вниз, F – сила упругости растянутой пружины вертикально вверх. Величина сила упругости пружины в указанном положении равна: F = c( ст + x). 4 МИ: составим для точки дифференциальное уравнение свободных колебаний и начальные условия движения : 5. Подставив данные, приведем дифференциальное уравнение к классическому виду: : : Применяя метод универсальной подстановки, проинтегрируем дифференциальное уравнение. В уравнении свободных колебаний постоянные интегрирования определены из начальных условий. Окончательно, уравнение свободных колебаний имеет вид:

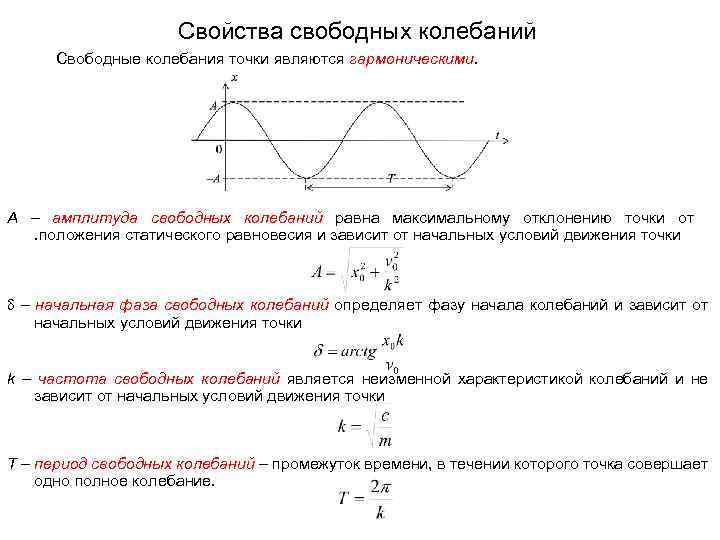Свойства свободных колебаний Свободные колебания точки являются гармоническими. А – амплитуда свободных колебаний равна максимальному отклонению точки от. положения статического равновесия и зависит от начальных условий движения точки – начальная фаза свободных колебаний определяет фазу начала колебаний и зависит от начальных условий движения точки k – частота свободных колебаний является неизменной характеристикой колебаний и не зависит от начальных условий движения точки T – период свободных колебаний – промежуток времени, в течении которого точка совершает одно полное колебание.

Вынужденные колебания материальной точки • Пусть в задаче о свободных колебаниях точки на неё помимо восстанавливающей силы F действует сила возмущающая Q, величина которой изменяется по гармоническому закону: P – частота возмущающей силы. Дифференциальное уравнение вынужденных колебаний точки имеет вид: Приведем дифференциальное уравнение вынужденных колебаний к классическому виду: Полное решение неоднородного дифференциального уравнения равно сумме решений : и представляет собой комбинацию свободных и вынужденных колебаний точки Постоянная B определяется подстановкой решения в дифференциальное уравнение: Резонанс Если частота возмущающей силы равна частоте свободных колебаний точки: p=k, происходит резонанс: размахи вынужденных колебаний неограниченно возрастают со временем. В этом случае уравнение вынужденных колебаний точки имеет вид:

Свойства вынужденных колебаний Амплитуда и начальная фаза свободных колебаний зависят от начальных условий движения точки Частота и период свободных колебаний являются неизменными характеристиками колебаний и не зависят от начальных условий движения точки Частота вынужденных колебаний равна частоте возмущающей силы Амплитуда вынужденных колебаний не зависит от начальных условий движения точки 0 – статическое отклонение точки под действием силы Q 0 – коэффициент динамичности показывает, во сколько раз амплитуда вынужденных колебаний больше статического отклонения 0, зависит от отношения частот z вынужденных и свободных колебаний точки.

Сопротивление при свободных колебаниях • Пусть в задаче о свободных колебаниях точки на неё помимо восстанавливающей силы F действует сила сопротивления R, величина которой пропорциональна скорости точки: Дифференциальное уравнение затухающих колебаний точки имеет вид: Приведем дифференциальное уравнение затухающих колебаний к классическому виду: Решение дифференциального уравнения имеет вид затухающих колебаний, если n < k: Решение дифференциального уравнения описывает апериодическое движение При n > k: При n = k:

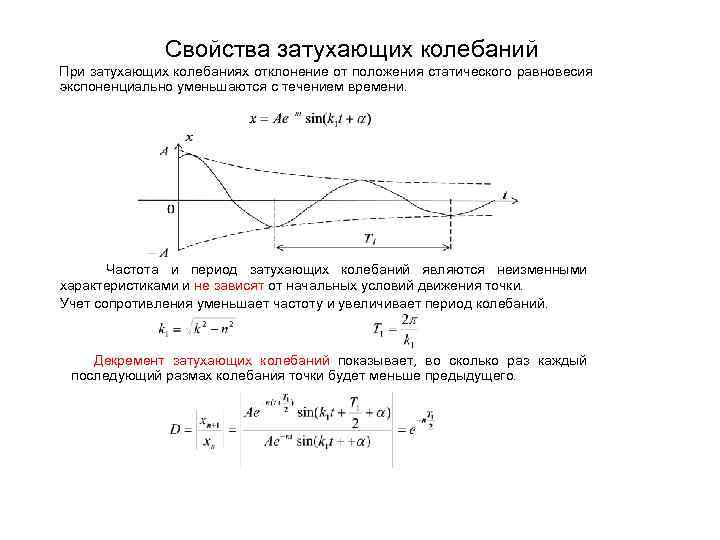Свойства затухающих колебаний При затухающих колебаниях отклонение от положения статического равновесия экспоненциально уменьшаются с течением времени. Частота и период затухающих колебаний являются неизменными характеристиками и не зависят от начальных условий движения точки. Учет сопротивления уменьшает частоту и увеличивает период колебаний. Декремент затухающих колебаний показывает, во сколько раз каждый последующий размах колебания точки будет меньше предыдущего.

Сопротивление при вынужденных колебаниях • Пусть в задаче о вынужденных колебаниях точки на неё помимо восстанавливающей силы F и возмущающей Q силы действует сила сопротивления R, величина которой пропорциональна скорости точки: Дифференциальное уравнение точки в этом случае имеет вид: Приведем это дифференциальное уравнение к виду: Полное решение неоднородного дифференциального уравнения равно сумме решений : и представляет собой комбинацию свободных и вынужденных колебаний точки при n < k: Свободные колебания являются затухающими при любых значениях n и k Постоянные интегрирования A и определяются из начальных условий движения Вынужденные колебания являются незатухающими гармоническими колебаниями Постоянные B и определяются подстановкой в дифференциальное уравнение:

Общие свойства вынужденных колебаний 1. Амплитуда вынужденных колебаний не зависит от начальных условий движения 2. Вынужденные колебания при наличии сопротивления не затухают 3. Частота вынужденных колебаний равна частоте возмущающей силы и от характеристик колеблющейся системы не зависит. Возмущающая сила «навязывает» системе свою частоту колебаний 4. Даже при малой возмущающей силе Q 0 можно получить вынужденные колебания большой амплитуды, если сопротивление мало, а частота вынужденных колебаний p близка частоте свободных колебаний k 5. Даже при , больших значениях возмущающей силы Q 0 можно вынужденные колебания можно сделать сколь угодно малыми, если частота вынужденных колебаний p будет много больше частоты свободных колебаний k