tema_5.ppt
- Количество слайдов: 35
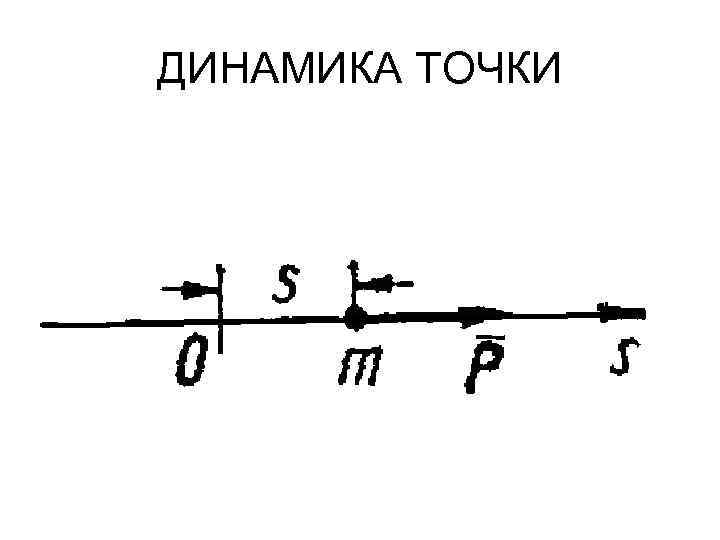
 ДИНАМИКА ТОЧКИ Прямолинейное движение точки Дифференциальное уравнение прямолинейного движения точки. Если отнести точку с массой m, находящуюся под действием силы Р, к координате s, дифференциальное уравнение движения имеет вид: md 2 s/dt 2= P
ДИНАМИКА ТОЧКИ Прямолинейное движение точки Дифференциальное уравнение прямолинейного движения точки. Если отнести точку с массой m, находящуюся под действием силы Р, к координате s, дифференциальное уравнение движения имеет вид: md 2 s/dt 2= P
 ДИНАМИКА ТОЧКИ
ДИНАМИКА ТОЧКИ
 ДИНАМИКА ТОЧКИ При задании закона движения s = f(t) (прямая или первая задача динамики) сила находится двукратным дифференцированием. При задании силы Р=P(t, s, v) (обратная или вторая задача динамики) закон движения находится интегрированием дифференциального уравнения движения.
ДИНАМИКА ТОЧКИ При задании закона движения s = f(t) (прямая или первая задача динамики) сила находится двукратным дифференцированием. При задании силы Р=P(t, s, v) (обратная или вторая задача динамики) закон движения находится интегрированием дифференциального уравнения движения.
 ДИНАМИКА ТОЧКИ Две постоянные интегрирования С 1 и С 2 определяются из начальных условий: при t = t 0, s = s 0, v = v 0. Когда P зависит только от одной переменной (t, S или v), задача решается так, как рассмотрено ранее в разделе «Основные задачи кинематики точки» (случаи 4— 6)
ДИНАМИКА ТОЧКИ Две постоянные интегрирования С 1 и С 2 определяются из начальных условий: при t = t 0, s = s 0, v = v 0. Когда P зависит только от одной переменной (t, S или v), задача решается так, как рассмотрено ранее в разделе «Основные задачи кинематики точки» (случаи 4— 6)
 Криволинейное движение точки Дифференциальные уравнения криволинейного движения. В декартовых координатах уравнения движения свободной материальной точки имеют вид тaх = X; maу = Y; maz = Z, где т - масса точки; aх, aу, az - ее ускорения; X, Y, Z - проекции действующей силы, являющиеся вообще функциями от t, х, у, z, vх, vу, vz, на оси координат.
Криволинейное движение точки Дифференциальные уравнения криволинейного движения. В декартовых координатах уравнения движения свободной материальной точки имеют вид тaх = X; maу = Y; maz = Z, где т - масса точки; aх, aу, az - ее ускорения; X, Y, Z - проекции действующей силы, являющиеся вообще функциями от t, х, у, z, vх, vу, vz, на оси координат.
 Криволинейное движение точки Шесть постоянных интегрирования определяются по начальным условиям: при t = t 0 (обычно t 0 = 0); х = х0; у=у0: z = z 0; vx=vx 0; vу=vу0: vz =vz 0. В случае несвободной точки к X, У, Z добавляются реакции связи Nx, NY, Nz, .
Криволинейное движение точки Шесть постоянных интегрирования определяются по начальным условиям: при t = t 0 (обычно t 0 = 0); х = х0; у=у0: z = z 0; vx=vx 0; vу=vу0: vz =vz 0. В случае несвободной точки к X, У, Z добавляются реакции связи Nx, NY, Nz, .
 Криволинейное движение точки В естественной форме (т. e. в проекциях на касательную, главную нормаль и бинормаль) уравнения движения свободной материальной точки имеют вид mdv/dt = Pt; mv 2/ρ = Рn; 0 = Рb где ρ - радиус кривизны траектории; Pt, Рn, Рb - проекции действующей силы.
Криволинейное движение точки В естественной форме (т. e. в проекциях на касательную, главную нормаль и бинормаль) уравнения движения свободной материальной точки имеют вид mdv/dt = Pt; mv 2/ρ = Рn; 0 = Рb где ρ - радиус кривизны траектории; Pt, Рn, Рb - проекции действующей силы.
 Движение точки переменной массы Точкой переменной массы называется материальная точка, масса которой изменяется вследствие присоединения к ней или отделения от нее некоторой части массы; эти массы не возникают и не исчезают, а только вводятся в рассмотрение или исключаются из него при решении поставленной задачи.
Движение точки переменной массы Точкой переменной массы называется материальная точка, масса которой изменяется вследствие присоединения к ней или отделения от нее некоторой части массы; эти массы не возникают и не исчезают, а только вводятся в рассмотрение или исключаются из него при решении поставленной задачи.
 Движение точки переменной массы При этом предполагается, во-первых, можно пренебречь относительным перемещением центра инерции вследствие изменения массы, а во-вторых, можно пренебречь кинематическими элементами вращательного движения по сравнению с кинематическими элементами поступательного движения. Предполагается также, что масса может быть выражена в виде непрерывной функции от времени m = m(t).
Движение точки переменной массы При этом предполагается, во-первых, можно пренебречь относительным перемещением центра инерции вследствие изменения массы, а во-вторых, можно пренебречь кинематическими элементами вращательного движения по сравнению с кинематическими элементами поступательного движения. Предполагается также, что масса может быть выражена в виде непрерывной функции от времени m = m(t).
 Движение точки переменной массы Уравнение Мещерского, является основным уравнением динамики точки переменной массы, ma=P+Pреакт где m — масса точки в данный момент времени; а - ее ускорение (точнее ускорение центра инерции); Р — приложенная сила; Рреакт - реактивная сила
Движение точки переменной массы Уравнение Мещерского, является основным уравнением динамики точки переменной массы, ma=P+Pреакт где m — масса точки в данный момент времени; а - ее ускорение (точнее ускорение центра инерции); Р — приложенная сила; Рреакт - реактивная сила
 Движение точки переменной массы Реактивная сила равна: Рреакт = (u-v)dm/dt где v -абсолютная скорость массы точки m(t) в данный момент времени; и - абсолютная скорость массы, присоединяющейся (dm > 0) или отделяющейся (dm < 0).
Движение точки переменной массы Реактивная сила равна: Рреакт = (u-v)dm/dt где v -абсолютная скорость массы точки m(t) в данный момент времени; и - абсолютная скорость массы, присоединяющейся (dm > 0) или отделяющейся (dm < 0).
 Общие теоремы динамики точки Количеством движения материальной точки называется вектор К= mv с проекциями mvx, mvy, mvz. Импульсом силы за промежуток времени t называется вектор I =0 ∫t Pdt с проекциями 0 ∫t. X dt, 0 ∫t Y dt, 0 ∫t Z dt. Размерность K такая же, как и размерность импульса.
Общие теоремы динамики точки Количеством движения материальной точки называется вектор К= mv с проекциями mvx, mvy, mvz. Импульсом силы за промежуток времени t называется вектор I =0 ∫t Pdt с проекциями 0 ∫t. X dt, 0 ∫t Y dt, 0 ∫t Z dt. Размерность K такая же, как и размерность импульса.
 Общие теоремы динамики точки Геометрическое приращение количества движения материальной точки за некоторый промежуток времени равно импульсу силы, за тот же промежуток времени: mvt + mv 0 =0 ∫t P dt где vt и v 0 - скорости точки соответственно в конечный и в начальный моменты времени.
Общие теоремы динамики точки Геометрическое приращение количества движения материальной точки за некоторый промежуток времени равно импульсу силы, за тот же промежуток времени: mvt + mv 0 =0 ∫t P dt где vt и v 0 - скорости точки соответственно в конечный и в начальный моменты времени.
 Общие теоремы динамики точки Момент количества движения материальной точки относительно центра и оси определяется совершенно так же, как момент силы. Момент количества движения точки относительно начала координат есть векторное произведение радиуса-вектора точки на ее количество движения: Go = r mv.
Общие теоремы динамики точки Момент количества движения материальной точки относительно центра и оси определяется совершенно так же, как момент силы. Момент количества движения точки относительно начала координат есть векторное произведение радиуса-вектора точки на ее количество движения: Go = r mv.
 Общие теоремы динамики точки Моменты количества движения точки относительно осей координат: Gx = m (yvz — zvy); Gy = m(zvx — xvz); Gz = m(xvу —yvx)
Общие теоремы динамики точки Моменты количества движения точки относительно осей координат: Gx = m (yvz — zvy); Gy = m(zvx — xvz); Gz = m(xvу —yvx)
 Общие теоремы динамики точки Теорема моментов количества движения. Производная по времени от момента количества движения материальной точки относительно некоторого неподвижного центра равна моменту приложенной силы относительно этого центра: d. G 0/dt = M 0(P)
Общие теоремы динамики точки Теорема моментов количества движения. Производная по времени от момента количества движения материальной точки относительно некоторого неподвижного центра равна моменту приложенной силы относительно этого центра: d. G 0/dt = M 0(P)
 Общие теоремы динамики точки Кинетической энергией, или живой силой материальной точки, называется половина произведения массы точки на квадрат ее скорости: T = mv 2 /2 Т имеет размерность работы
Общие теоремы динамики точки Кинетической энергией, или живой силой материальной точки, называется половина произведения массы точки на квадрат ее скорости: T = mv 2 /2 Т имеет размерность работы
 Общие теоремы динамики точки Теорема кинетической энергии. Приращение кинетической энергии материальной точки на некотором перемещении (элементарном или конечном) равно работе приложенных сил на этом перемещении: mv 2 /2 – mv 02 /2 = A где А есть работа всех сил или работа равнодействующей.
Общие теоремы динамики точки Теорема кинетической энергии. Приращение кинетической энергии материальной точки на некотором перемещении (элементарном или конечном) равно работе приложенных сил на этом перемещении: mv 2 /2 – mv 02 /2 = A где А есть работа всех сил или работа равнодействующей.
 Общие теоремы динамики точки Если силы имеют потенциал, то имеет место закон сохранения механической энергии: Т + П = Т 0 + П 0 где П—потенциальная энергия.
Общие теоремы динамики точки Если силы имеют потенциал, то имеет место закон сохранения механической энергии: Т + П = Т 0 + П 0 где П—потенциальная энергия.
 ДИНАМИКА СИСТЕМЫ Общие теоремы динамики системы Количеством движения системы или, точнее, главным вектором количества движения системы называется геометрическая сумма количества движения всех точек системы
ДИНАМИКА СИСТЕМЫ Общие теоремы динамики системы Количеством движения системы или, точнее, главным вектором количества движения системы называется геометрическая сумма количества движения всех точек системы
 Общие теоремы динамики системы Теорема количества движения (в дифференциальной форме). Производная по времени от главного вектора количества движения системы равна главному вектору внешних сил d. K/dt=R=∑Pi
Общие теоремы динамики системы Теорема количества движения (в дифференциальной форме). Производная по времени от главного вектора количества движения системы равна главному вектору внешних сил d. K/dt=R=∑Pi
 Общие теоремы динамики системы Теорема импульсов (теорема количества движения в конечной форме). Геометрическое приращение главного вектора количества движения системы за некоторый промежуток времени равно сумме импульсов всех внешних сил за тот же промежуток: К – Ко = ∑Ii В случае уравновешивания внешних сил К = Ко = const.
Общие теоремы динамики системы Теорема импульсов (теорема количества движения в конечной форме). Геометрическое приращение главного вектора количества движения системы за некоторый промежуток времени равно сумме импульсов всех внешних сил за тот же промежуток: К – Ко = ∑Ii В случае уравновешивания внешних сил К = Ко = const.
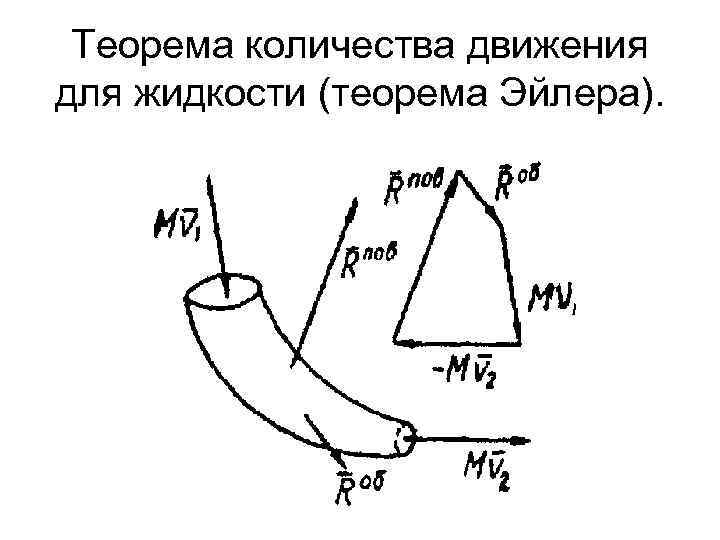
 Общие теоремы динамики системы Теорема количества движения для жидкости (теорема Эйлера). Главные векторы объемных и поверхностных сил и векторы количества движения массы жидкости, протекающей в единицу времени через входное сечение трубы и с обратным знаком через выходное, образуют замкнутый многоугольник: Mv 1 - Mv 2 + Roб +Rnoв = 0, где М = Q/g, a Q — весовой расход жидкости.
Общие теоремы динамики системы Теорема количества движения для жидкости (теорема Эйлера). Главные векторы объемных и поверхностных сил и векторы количества движения массы жидкости, протекающей в единицу времени через входное сечение трубы и с обратным знаком через выходное, образуют замкнутый многоугольник: Mv 1 - Mv 2 + Roб +Rnoв = 0, где М = Q/g, a Q — весовой расход жидкости.
 Теорема количества движения для жидкости (теорема Эйлера).
Теорема количества движения для жидкости (теорема Эйлера).
 Теорема о движении центра инерции (также центра масс, центра тяжести). Центр масс системы движется как материальная точка, в которой сосредоточена вся масса системы и к которой приложены все внешние силы, действующие на систему.
Теорема о движении центра инерции (также центра масс, центра тяжести). Центр масс системы движется как материальная точка, в которой сосредоточена вся масса системы и к которой приложены все внешние силы, действующие на систему.
 Теорема о движении центра инерции Если хс, ус, zc — координаты центра масс, ас — его ускорение, М — масса системы, R — главный вектор внешних сил, то Мас = R. В координатной форме дифференциальные уравнения движения центра масс Мaхс = Rx; Mayс = Ry; Mazc = Rz.
Теорема о движении центра инерции Если хс, ус, zc — координаты центра масс, ас — его ускорение, М — масса системы, R — главный вектор внешних сил, то Мас = R. В координатной форме дифференциальные уравнения движения центра масс Мaхс = Rx; Mayс = Ry; Mazc = Rz.
 Кинетический момент Главным моментом количеств движения системы или кинетическим моментом системы относительно некоторого центра (например, начала координат) называется геометрическая сумма моментов количеств движения всех точек системы относительно этого центра: Go = ∑ mom 0(mivi) = ∑rimivi
Кинетический момент Главным моментом количеств движения системы или кинетическим моментом системы относительно некоторого центра (например, начала координат) называется геометрическая сумма моментов количеств движения всех точек системы относительно этого центра: Go = ∑ mom 0(mivi) = ∑rimivi
 Кинетический момент Проекции Go на оси координат, проходящие через О, называются главными моментами количеств движения системы или кинетическими моментами относительно осей; они равны соответственным алгебраическим суммам моментов относительно этих осей:
Кинетический момент Проекции Go на оси координат, проходящие через О, называются главными моментами количеств движения системы или кинетическими моментами относительно осей; они равны соответственным алгебраическим суммам моментов относительно этих осей:
 Кинетический момент Gx = ∑ momx(mivi) = ∑mi (yiviz - ziviy); Gy = ∑ momy(mivi) = ∑ mi (zivix - xiviz); Gz = ∑ momz(mivi) = ∑ mi (xiviy - yivix).
Кинетический момент Gx = ∑ momx(mivi) = ∑mi (yiviz - ziviy); Gy = ∑ momy(mivi) = ∑ mi (zivix - xiviz); Gz = ∑ momz(mivi) = ∑ mi (xiviy - yivix).
 теорема о кинетическом моменте Производная по времени от кинетического момента системы относительно некоторого центра (неподвижного или же относительно центра масс) равна главному моменту внешних сил относительно того же центра: d. G 0/dt = Lo = ∑M 0(Pi)
теорема о кинетическом моменте Производная по времени от кинетического момента системы относительно некоторого центра (неподвижного или же относительно центра масс) равна главному моменту внешних сил относительно того же центра: d. G 0/dt = Lo = ∑M 0(Pi)
 Кинетическая энергия системы Кинетической энергией или живой силой системы называется сумма произведений масс всех ее точек на квадраты их скоростей: T = ∑mivi 2/2
Кинетическая энергия системы Кинетической энергией или живой силой системы называется сумма произведений масс всех ее точек на квадраты их скоростей: T = ∑mivi 2/2
 Кинетическая энергия системы равна сумме кинетической энергии центра масс системы, в котором сосредоточена вся ее масса, и кинетической энергии в относительном движении системы по отношению к осям, проходящим через центр масс и движущимся поступательно: T = Mvc 2/2 + Tотн
Кинетическая энергия системы равна сумме кинетической энергии центра масс системы, в котором сосредоточена вся ее масса, и кинетической энергии в относительном движении системы по отношению к осям, проходящим через центр масс и движущимся поступательно: T = Mvc 2/2 + Tотн
 Теорема кинетической энергии для системы Приращение кинетической энергии системы на некотором перемещении (элементарном или конечном) равно сумме работ всех приложенных сил как внешних, так и внутренних: T – T 0 = ∑Aвнешн + ∑Aвнут Если система неизменяемая, то ∑Aвнут = 0
Теорема кинетической энергии для системы Приращение кинетической энергии системы на некотором перемещении (элементарном или конечном) равно сумме работ всех приложенных сил как внешних, так и внутренних: T – T 0 = ∑Aвнешн + ∑Aвнут Если система неизменяемая, то ∑Aвнут = 0
 Общие принципы динамики системы Принцип Даламбера. Если ко всем точкам системы приложить силы инерции, то активные силы, реакции связей и силы инерции будут уравновешиваться. Уравнения равновесия составляются таким же образом, как в статике, и носят название уравнений кинетостатики
Общие принципы динамики системы Принцип Даламбера. Если ко всем точкам системы приложить силы инерции, то активные силы, реакции связей и силы инерции будут уравновешиваться. Уравнения равновесия составляются таким же образом, как в статике, и носят название уравнений кинетостатики
 Общее уравнение кинетостатики Объединение принципа возможных перемещений и принципа Даламбера гласит: сумма элементарных работ всех активных сил, приложенных к материальной системе, подчиненной идеальным неосвобождающим связям, и сил инерции на всяком возможном перемещении равна нулю.
Общее уравнение кинетостатики Объединение принципа возможных перемещений и принципа Даламбера гласит: сумма элементарных работ всех активных сил, приложенных к материальной системе, подчиненной идеальным неосвобождающим связям, и сил инерции на всяком возможном перемещении равна нулю.


