Динамика материальной точки 1 Основные понятия динамики

Динамика материальной точки. 1. Основные понятия динамики:

• А) Си ла — векторная физическая величина, являющаяся мерой интенсивности воздействия на данное тело других тел, а также полей. Приложенная к массивному телу сила является причиной изменения его скорости или возникновения в нём деформаций. (F). • Сила как векторная величина характеризуется модулем, направлением и «точкой» приложения силы. Последним параметром понятие о силе, как векторе в физике, отличается от понятия о векторе в векторной алгебре, где равные по модулю и направлению векторы, независимо от точки их приложения, считаются одним и тем же вектором. В физике эти векторы называются свободными векторами. В механике чрезвычайно распространено представление о связанных векторах, начало которых закреплено в определённой точке пространства или же может находиться на линии, продолжающей направление вектора (скользящие векторы).

• • • Б) Ма сса (от греч. μάζα) — скалярная физическая величина, одна из важнейших величин физике. Первоначально (XVII—XIX века) она характеризовала «количество вещества» в физическом объекте, от которого, по представлениям того времени, зависели как способность объекта сопротивляться приложенной силе (инертность), так и гравитационныесвойства — вес. Тесно связана с понятиями «энергия» и «импульс» (по современным представлениям — масса эквивалентна энергии покоя). (M, m). В современной физике понятие «количество вещества» имеет другой смысл, а концепцию «масса» можно трактовать несколькими способами: Пассивная гравитационная масса показывает, с какой силой тело взаимодействует с внешними гравитационными полями — фактически эта масса положена в основу измерения массы взвешиванием в современной метрологии. Активная гравитационная масса показывает, какое гравитационное поле создаёт само это тело — гравитационные массы фигурируют в законе всемирного тяготения. Инертная масса характеризует меру инертности тел и фигурирует в одной из формулировок второго закона Ньютона. Если произвольная сила в инерциальной системе отсчёта одинаково ускоряет разные исходно неподвижные тела, этим телам приписывают одинаковую инертную массу.

• • • В) И мпульс си лы — это векторная физическая величина, равная произведению силы на время её действия, мера воздействия силы на тело за данный промежуток времени (впоступательном движении). (Ньютон*сек. ). Г) Момент силы — векторная физическая величина, равная произведению радиус-вектора, проведенного от оси вращения к точке приложения силы, на вектор этой силы. Характеризует вращательное действие силы на твёрдоетело. (Ньютон-метр). В физике момент силы можно понимать как «вращающая сила» . В системе СИ единицами измерения для момента силы является Ньютон-метр. Момент силы иногда называют моментом пары сил, это понятие возникло в трудах Архимеда над рычагами. В простейшем случае, если сила приложена к рычагу перпендикулярно ему, момент силы определяется как произведение величины этой силы на расстояние до оси вращения рычага, есть момент силы. Например, сила в 3 ньютона, приложенная к рычагу на расстоянии 2 метров от его оси вращения, создаёт такой же момент, что и сила в 1 ньютон, приложенная к рычагу на расстоянии 6 метров до оси вращения. Более точно, момент силы частицы определяется как векторное произведение: где — сила, действующая на частицу, а — радиус-вектор частицы.

• • • Д) Моме нт и мпульса характеризует количество вращательного движения. Величина, зависящая от того, сколько массы вращается, как она распределена относительно оси вращения и с какой скоростью происходит вращение. м 2·кг·с− 1 Следует учесть, что вращение здесь понимается в широком смысле, не только как регулярное вращение вокруг оси. Например, даже при прямолинейном движении тела мимо произвольной воображаемой точки, не лежащей на линии движения, оно также обладает моментом импульса. Наибольшую, пожалуй, роль момент импульса играет при описании собственно вращательного движения. Однако крайне важен и для гораздо более широкого класса задач (особенно — если в задаче есть центральная или осевая симметрия, но не только в этих случаях). Момент импульса относительно точки — это псевдовектор, а момент импульса относительно оси — псевдоскаляр. Момент импульса замкнутой системы сохраняется. Е) Материа льная то чка — простейшая физическая модель в механике — тело, размеры которого допустимо считать бесконечно малыми в пределах допущений исследуемой задачи. Практически под материальной точкой понимают обладающее массой тело, размерами и формой которого можно пренебречь при решении данной задачи.

2. Основные законы динамики: • • • А) Первый закон Ньютона. Существуют такие системы отсчёта, называемые инерциальными, относительно которых материальная точка при отсутствии внешних воздействий сохраняет величину и направление своей скорости неограниченно долго. Первый закон Ньютона утверждает, что существуют системы отсчета, в которых тела сохраняют состояние покоя или равномерного прямолинейного движения при отсутствии действий на них со стороны других тел или при взаимной компенсации этих воздействий. Такие системы отсчета называются инерциальными. Ньютон предположил, что каждый массивный объект имеет определенный запас инерции, который характеризует «естественное состояние» движения этого объекта. Эта идея отрицает взгляд Аристотеля, который рассматривал покой «естественным состоянием» объекта. Первый закон Ньютона противоречит аристотелевской физике, одним из положений которой является утверждение о том, что тело может двигаться с постоянной скоростью лишь под действием силы. Тот факт, что в механике Ньютона в инерциальных системах отсчёта покой физически неотличим от равномерного прямолинейного движения, является обоснованием принципа относительности Галилея. Среди совокупности тел принципиально невозможно определить какие из них находится «в движении» , а какие «покоятся» . Говорить о движении можно лишь относительно какой-либо системы отсчета. Законы механики выполняются одинаково во всех инерциальных системах отсчета, другими словами все они механически эквивалентны. Последнее следует из так называемых преобразований Галилея.

• • • Например, законы механики абсолютно одинаково выполняются в кузове грузовика, когда тот едет по прямому участку дороги с постоянной скоростью и когда стоит на месте. Человек может подбросить мячик вертикально вверх и поймать его через некоторое время на том же самом месте вне зависимости от того движется ли грузовик равномерно и прямолинейно или покоится. Для него мячик летит по прямой. Однако для стороннего наблюдателя, находящегося на земле, траектория движения мячика имеет вид параболы. Это связано с тем, что мячик относительно земли движется во время полета не только вертикально, но и горизонтально по инерции в сторону движения грузовика. Для человека, находящегося в кузове грузовика не имеет значения движется ли последний по дороге, или окружающий мир перемещается с постоянной скоростью в противоположном направлении, а грузовик стоит на месте. Таким образом, состояние покоя и равномерного прямолинейного движения физически неотличимы друг от друга. Инерциа льная систе ма отсчёта (ИСО) — система отсчёта, в которой справедлив закон инерции: все свободные тела (то есть такие, на которые не действуют внешние силы или действие этих сил компенсируется) движутся прямолинейно и равномерно или покоятся. Инерциальной называется система отсчёта, по отношению к которой пространство является однородным и изотропным, а время — однородным.

• • • Б) Второй закон Ньютона в современной формулировке звучит так: в инерциальной системе отсчета скорость изменения импульса материальной точки равна векторной сумме всех сил, действующих на эту точку. где − импульс материальной точки, − суммарная сила, действующая на материальную точку. Второй закон Ньютона гласит, что действие несбалансированных сил приводит к изменению импульса материальной точки. По определению импульса: где − масса, − скорость. По правилу нахождения производной произведения: Если масса материальной точки остается неизменной, то производная по времени от массы равна нулю, и уравнение принимает вид: Учитывая определение ускорения точки, второй закон Ньютона принимает вид: Считается, что это «вторая самая известная формула в физике» , хотя сам Ньютон никогда явным образом не записывал свой второй закон в этом виде.

• • • Поскольку в любой инерциальной системе отсчёта ускорение тела одинаково и не меняется при переходе от одной системы к другой, то и сила инвариантна по отношению к такому переходу. Во всех явлениях природы сила, независимо от своего происхождения, проявляется только в механическом смысле, то есть как причина нарушения равномерного и прямолинейного движения тела в инерциальной системе координат. Обратное утверждение, т. е установление факта такого движения, не свидетельствует об отсутствии действующих на тело сил, а лишь о том, что действия этих сил взаимно уравновешиваются. Иначе: их векторная сумма есть вектор с модулем, равным нулю. На этом основано измерение величины силы, когда она компенсируется силой, величина которой известна. Второй закон Ньютона позволяет измерять величину силы. Например, знание массы планеты и ее центростремительного ускорения при движении по орбите позволяет вычислить величину силыгравитационного притяжения, действующую на эту планету со стороны Солнца.

• • В) Третий закон Ньютона. Для любых двух тел (назовем их тело 1 и тело 2) третий закон Ньютона утверждает, что сила действия тела 1 на тело 2, сопровождается появлением равной по модулю, но противоположной по направлению силы, действующей на тело 1 со стороны тела 2. Математически закон записывается так: Этот закон означает, что силы всегда возникают парами «действиепротиводействие» . Если тело 1 и тело 2 находятся в одной системе, то суммарная сила в системе, обусловленная взаимодействиемэтих тел равна нулю: Это означает, что в замкнутой системе не существует несбалансированных внутренних сил. Это приводит к тому, что центр масс замкнутой системы (то есть той, на которую не действуют внешние силы) не может двигаться с ускорением. Отдельные части системы могут ускоряться, но лишь таким образом, что система в целом остается в состоянии покоя или равномерного прямолинейного движения. Однако в том случае, если внешние силы подействуют на систему, то ее центр масс начнет двигаться с ускорением, пропорциональным внешней результирующей силе и обратно пропорциональным массе системы.

• Зако н сохране ния и мпульса утверждает, что векторная сумма импульсов всех тел (или частиц) замкнутой системы есть величина постоянная. • В классической механике закон сохранения импульса обычно выводится как следствие законов Ньютона. Из законов Ньютона можно показать, что при движении в пустом пространстве импульс сохраняется во времени, а при наличии взаимодействия скорость его изменения определяется суммой приложенных сил.

Задача • • Человек массой 50 кг поднимается в лифте с ускорением 1, 5 м/с2. Найти давление, создаваемое человеком на пол лифта. Дано: m = 50 кг а = 1, 5 м/с2 Найти: F - ? Решение: Для составления чертежа следует решить вопрос: человека или лифт целесообразно принять за материальную точку? Так как все взаимодействия человека с другими телами известны, целесообразно именно человека принять за материальную точку. Изобразив на основном чертеже лифт и человека, укажем оси проецирования и направление ускорения. Проанализируем взаимодействие человека с Землей. В результате этого взаимодействия возникают две силы: одна из них приложена к человеку (mg), другая по третьему закону Ньютона - к Земле. Из этих двух сил на основной чертеж проставляем только силу тяжести (mg), поскольку она приложена к интересующей нас материальной точке (рис. 21). Если бы действовала только эта сила, человек начал бы свободно падать. Однако ситуация иная: он поднимается вверх с ускорением. Следовательно, выделенная нами материальная точка участвует во втором взаимодействии - человека и пола лифта.

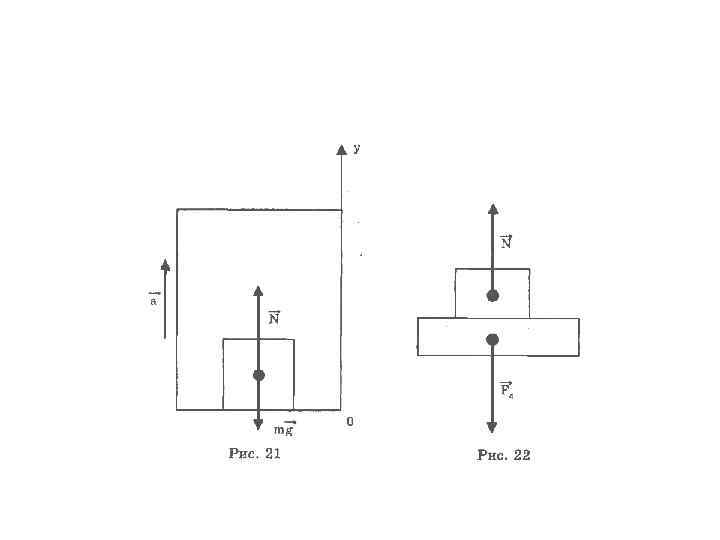
• Укажем на дополнительном чертеже расстановку сил (рис. 22). Человек оказывает давление на пол лифта (Fд), пол лифта действует на человека с силой упругости N. • Эти силы возникают соответственно третьему закону Ньютона. Нас интересует при этом только сила N, поскольку она приложена к выделенной материальной точке, и ее мы проставляем на основной чертеж. Других взаимодействий нет. • Поскольку на материальную точку действуют 2 силы, применяем ОУД:

• Проецируем векторы на ось Оу и получаем: • Отсюда находим N: • Ответ: человек давит на пол лифта с силой 575 Н.